用于监控过程均值的DMHWMA控制图

李禹平，朱永忠

(河海大学 理学院,江苏 南京 211100)

统计过程控制(Statistical Process Control , SPC)在现如今质量监测行业中扮演着重要的角色，是一种应用广泛的质量控制手段。应用SPC对生产过程进行控制最有效的一种形式就是通过绘制控制图来进行监测。常见的一元质量控制图有休哈特控制图、Page(1961)[1]提出的累积和(Cumulation Sum，CUSUM)控制图、Roberts(1959)[2]提出的指数加权移动平均(Exponentially Weighted Moving Average，EWMA)控制图等。上述提到的控制图都是针对一元的情况，只能针对一种质量特性进行监控。而随着社会生活的发展，在生产行业中需要监控的指标或者质量特性也越来越多，因此多元控制图也应运而生。相应地在一元控制图的基础上人们提出了针对多元情况的控制图。例如：Hotelling(1947)[3]提出了多元休哈特控制图、Lowry(1992)[4]提出了多元指数加权移动平均(Multivariate Exponentially Weighted Moving Average,MEWMA)控制图、Crosier(1988)[5]提出了多元累积和(Multivariate Cumulation Sum, MCUSUM)控制图。Shamm等(1992)[6]提出了双指数加权移动平均(Double Exponentially Weighted Moving Average ,DEWMA)控制图，提高了EWMA控制图对于数据发生小偏差时的检测能力。Haq (2017)[7]提出了混合指数加权移动平均(Hybrid Exponentially Weighted Moving Average， HEWMA)控制图，但其本质与DEWMA控制图并无较大差别。Abbass等(2018)[8]提出了一种新型一元记忆型控制图,称为均匀加权移动平均(Homogeneously Weighted Moving Average ，HWMA)控制图,这种控制图与之前的EWMA控制图的不同点是采用确定当前时刻对应数值的权重，将剩余权重平均分配给之前所有时刻对应的数值的方法。实验结果表明，HWMA控制图相比传统的一元记忆型控制图对于过程均值的变化更加敏感。Abid等(2020)[9]在Abbas提出的HWMA记忆型控制图的基础上提出了双均匀加权移动平均(Double Homogeneously Weighted Moving Average, DHWMA)记忆型控制图，但是其主要结构与之前的HWMA记忆型控制图并无本质变化，只是平滑系数由λ变成了λ2。Adeoti(2020)[10]提出了混合均匀加权移动平均(Hybrid Homogeneously Weighted Moving Average ，HHWMA)控制图，但是在Vasileios等(2021)[11]提出的一种拓展的双均匀加权移动平均(Double Homogeneously Weighted Moving Average, DHWMA)记忆型控制图的文章中指出HHWMA控制图统计量的方差是不正确的。而Vasileios等提出的DHWMA记忆型控制图的主要结构是通过模仿Shamm等(1992)[6]提出DEWMA控制图的构造过程而得到的，对于控制过程中小幅度的数据偏差的检测效果比之前提出的HWMA控制图、DEWMA控制图以及DHWMA控制图有很大提高。而在多元控制图中，HWMA控制图的多元形式已被提出，即多元HWMA控制图，其性能较之前已有的控制图有了很大提高。而DHWMA控制图的多元形式还没有被提出。

因此本文旨在提高多元控制图对于过程均值变化的检测能力，在Vasileios提出的DHWMA基础上，参照Adegoke等(2019)12]开发多元HWMA控制图和Alkahtani等(2012)[13]开发双多元指数加权移动平均(Double Multivariate Exponentially Weighted Moving Average，DMEWMA)控制图的思想，将其拓展成多元的形式，称为双多元均匀加权移动平均(Double Multivariate Homogeneously Weighted Moving Average ，DMHWMA)控制图。对于过程中均值变化的监测效果，DMHWMA控制图相比之前存在的多元EWMA控制图、多元CUSUM控制图、多元HWMA控制图有很大提高。

1 DMHWMA控制图

假设有m个p维随机变量X1,X2,…,Xm且服从均值为μ0，协方差为∑0的p维正态分布。本文监测变量过程均值的变化情况。

1.1 MHWMA控制图的主要表达式

MHWMA控制图的主要结构：

(1)

本文假定平滑系数矩阵对角线上的元素满足ω1=ω2=…=ωp=ω，则表达式(1)可写成如下形式：

1.2 DMHWMA控制图的主要表达式

1.2.1 主要结构

在MHWMA控制图的基础上，本文提出了DMHWMA记忆型控制图(样本容量n=1)，其主要结构为：

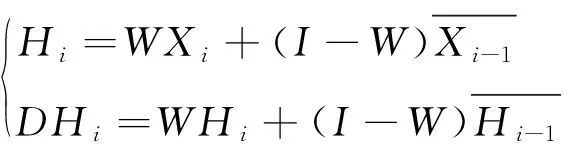
(2)

本文假定平滑系数矩阵对角线上的元素满足ω1=ω2=…=ωp=ω，则表达式(2)可写成如下形式：

(3)

1.2.2 表达式推导证明过程

DHi表达式与其协方差的表达式推导过程如下：

(1)i=1时，

E(DH1)=E(ω2X1+(1-ω2)μ0)=ω2E(X1)+(1-ω2)μ0=μ0

∑DH1=Var(DH1)=Var(ω2X1+(1-ω2)μ0)=ω4∑0

(2)i=2时，

E(DH2)=ω2E(X2)+2ω(1-ω)E(X1)+(1-ω)2μ0=μ0

∑DH2=Var(DH2)=Var(ω2X2+2ω(1-ω)X1+(1-ω)2μ0) =ω2(ω2+4(1-ω)2)∑0

(3)i>2时，

同理可验证

E(DHi)=μ0

因此统计量DHi的表达式如下:

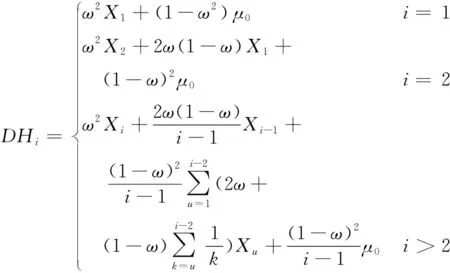
对于i时刻的统计量DHi的协方差矩阵表达式如下：

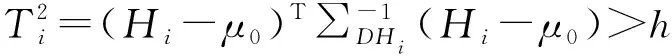
1.2.3 方向不变性

DMHWMA控制图具有方向不变性，DMHWMA控制图的平均运行长度特性只与偏移系数δ有关[3]-[4]，其中，其主要证明过程如下：

假设M是一个p×p的满秩矩阵，且有DH*=MDH。

(1)i=1时，

(2)i=2时同理可得。

(3)i>2时：

1.3 几种特殊情况

1.3.1 若ω=1

此时，统计量DHi=Xi，统计量∑DHi=∑0，DMHWMA记忆型控制图就变成了之前的记忆型χ2控制图，因此在ω=1时，采用DMHWMA控制图和采用记忆型MHWMA控制图对生产过程的监控效果一致。

1.3.2 若p=1

DHi的表达式：

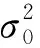
1.3.3 若n>1

统计量DHi的表达式中Xi需要用i时刻得到的一组内n个样本观察值的平均值代替，并且∑DHi的表达式更改为：

2 模拟对比分析

衡量一个控制图监控性能的好坏有许多种方法。其中最常用的就是用平均运行长度(ARL)这一特性来进行衡量。ARL指的是控制图首次发出失控信号而必须采集的样本数量集，一般地，称过程处于稳定状态时的ARL为ARL0，过程处于失控状态时的ARL为ARL1。在控制图检测过程中，我们希望过程处于稳定状态时，ARL0越大越好，过程失控时，ARL1越小越好。

本文采用R软件运用蒙特卡罗模拟方法对满足多元正态分布的数据进行抽样，随机模拟10000次，在控制ARL0为200的前提下计算本文提出的DMHWMA控制图与现有的多元控制图的ARL1，模拟结果如下：

表1 已知μ0和∑0,ARL0为200时 DMHWMA控制图的ARL

表2 μ0和∑0,ARL0为200时MHWMA控制图的ARL

表3 已知μ0和∑0，ARL0为200时MEWMA控制图的ARL

表4 已知μ0和∑0，ARL0为200时MCUSUM控制图的ARL

将p=2和p=5以上表格中各个控制图在δ取不同值时最小的ARL(即表1至表4中加粗的数字)取对数绘制曲线如图1、图2所示。

由表1至表4及图1、图2可知，

(1)固定ω值，δ越大，各个控制图对应的ARL1越小。

(2)固定某一δ。若δ值相对较小，则ω越小，控制图的监测敏感度越强。若δ值相对较大，则ω越大，控制图的监测敏感度越强。

(3)通过图1、图2以及对比上述表格中各个控制图对于不同程度的偏移的平均运行长度数值，可知不论是二维变量还是五维变量下过程均值发生哪种程度的偏移，DMHWMA控制图ARL的数值都是最小的。

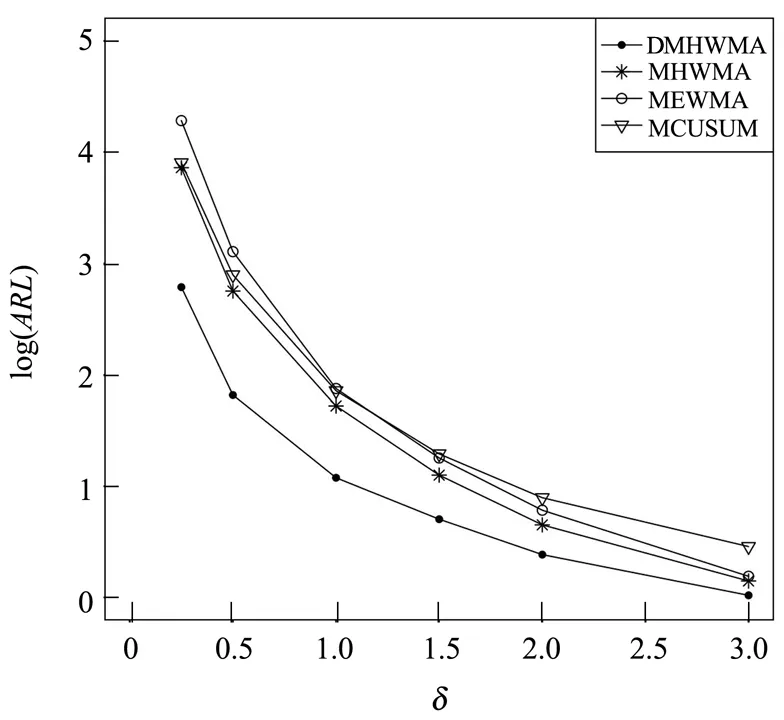
图1 p=2时DMHWMA、MHWMA、MEWMA、MCUSUM控制图在不同程度偏移下最优ARL对比

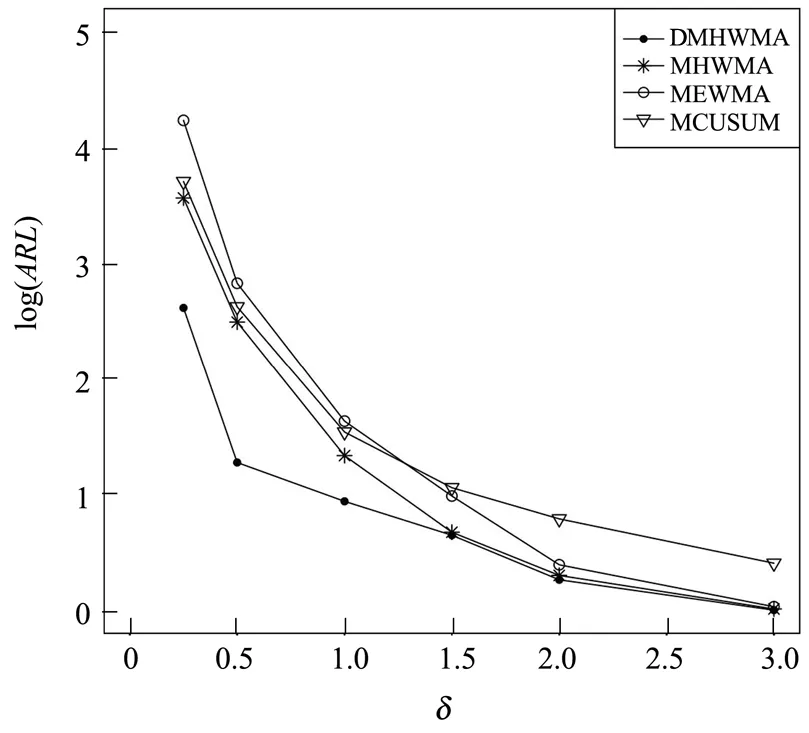
图2 p=5时DMHWMA、MHWMA、MEWMA、MCUSUM 控制图在不同程度偏移下最优ARL对比

3 实证分析

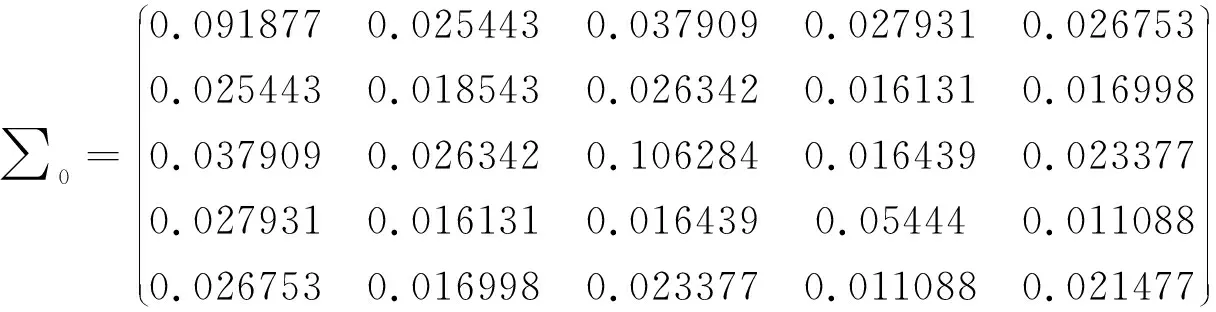
本文使用文献[14]的双金属恒温数据集，此数据集包含每个双金属恒温(黄铜和钢)的偏转、曲率、电阻率和硬度、低膨胀面和高膨胀面共5个属性的数据。第一阶段的过程数据样本量为m=28，且p=5。通过参考第一阶段过程的历史样本，运用传统无偏估计方法估计出了过程参数μ0和∑0。

DMHWMA(ω=0.2，h=10.74)

MHWMA(ω=0.2，h=17.05)

MEWMA(ω=0.2,h=16.30)

MCUSUM(k=0.25，h=15.25)

上述参数来源于表1至表4，以控制本例一期数据集的ARL0为200。二期数据各个控制图监控情况如图3至图6所示：

从图3到图6，对于二期数据的20个失控样本，其中DMHWMA控制图在第3个样本之后开始发出警报，MHWMA控制图在第6个样本之后开始发出警报，MEWMA控制图在第11个样本之后开始发出警报,而MCUSUM控制图在第18个样本后才发出警报。因此，从实例可以看出对于小偏差的失控数据DMHWMA控制图的检测效果要优于现有的MEWMA控制图、MHWMA控制图与MCUSUM控制图。

图3 DMHWMA控制图

图4 MHWMA控制图

图5 MEWMA控制图

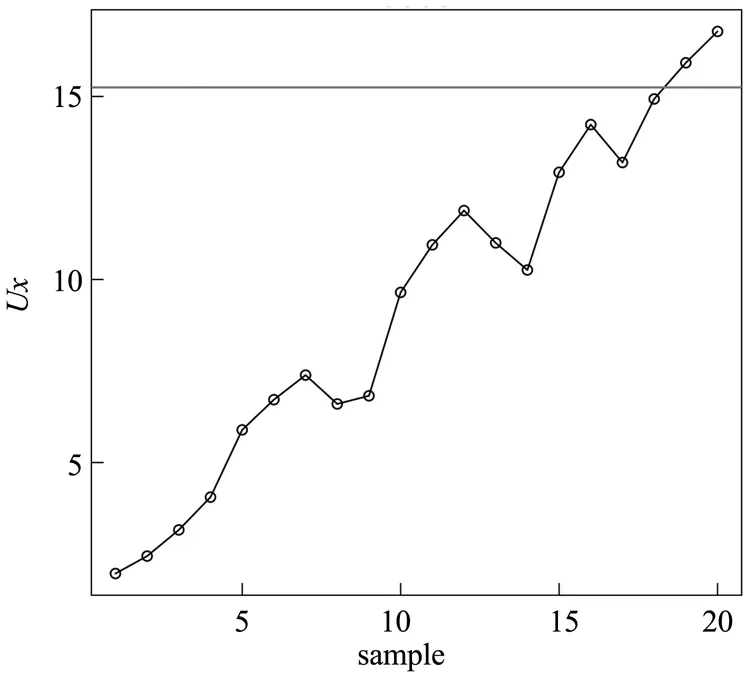
图6 MCUSUM控制图

4 结 论

提出了一个用于监测过程均值变化的双多元均匀加权移动平均控制图。运用蒙特卡罗模拟实验与MEWMA控制图、MHWMA控制图、MCUSUM控制图比较监测性能，实验结果表明，对于过程均值不同幅度的变化，DMHWMA控制图的检测效果都要优于其他控制图，特别是对于小幅度的偏移，DMHWMA控制图的监测效果优越性更加明显。并且使用一个实例数据验证了上述结论的正确性。因此，在监测多变量均值变化时，建议使用DMHWMA控制图进行监控。