水平荷载作用下框架结构内力计算的楼层转角法1

张年文

(广东石油化工学院 建筑工程学院，广东 茂名 525000)

反弯点法和D值法[1]是计算框架结构在水平荷载作用下内力的经典近似方法，在结构设计的初步设计阶段应用较多。D值法要查表确定柱的反弯点高度，使用不便。孟焕陵等[2]介绍了计算框架结构水平位移的三种方法，推荐采用Smith-Coull方法[3]计算水平位移。Hsiao[4]提出了一种求解框架结构的水平位移和内力的悬臂梁力矩分配法，把多跨框架分解成多榀相同的单跨框架，分别计算各单跨框架的内力。Hu等[5]假定同一楼层的节点位移和转角相等，利用计算机程序求解框架结构的水平位移，可以有效减少未知量的个数。R. Rahgozar等[6]提出了一个可以分析框架结构水平位移的数学模型。水平荷载作用下框架结构内力计算，据作者了解的信息，除了用计算机程序分析外无精度较高的近似求解方法。

力矩分配法是计算竖向荷载作用下连续梁、框架结构弯矩的经典渐近方法，该方法不能直接求解节点有水平位移的结构。本文提出了一种求解水平荷载作用下框架结构内力的近似方法，采用迭代计算每根柱(或者整个楼层柱)的节点转角，迭代过程与悬臂梁的力矩分配法过程类似，求解出所有柱的节点转角后，根据柱的节点转角、楼层剪力计算楼层的相对水平位移，然后根据转角位移方程计算梁、柱端初始弯矩(类似力矩分配法的固端弯矩)，采用力矩分配法求解梁、柱端弯矩。

1 基本方程

1.1 基本假定

水平荷载下框架结构水平位移、内力计算，采用如下假定：

(1) 框架结构的楼板为刚性楼板，只考虑楼板平动产生的水平位移；(2) 每个楼层梁、柱节点处的转角相等；(3) 所有荷载作用在楼层节点上；(4) 不考虑柱的轴向变形；(5) 柱底为固定端。

1.2 框架梁、柱端弯矩

不考虑柱的轴向变形，连接节点(i,j)(表示第i层的第j个节点)和节点(i,j+1)的梁端弯矩可表示为Mi,j+1,j=4ki,j,j+1θi,j+2ki,j,j+1θi,j+1,Mi,j,j+1=2ki,j,j+1θi,j+4ki,j,j+1θi,j+1。式中：Mi,j,j+1为梁在节点j+1端的端弯矩，最末的下标表示所在节点端；ki,j,j+1为梁的线刚度,ki,j,j+1=ki,j+1,j；θi,j为节点(i,j)的转角；柱端、梁端的弯矩、转角以顺时针方向为正，逆时针方向为负。

1.3 楼层剪力

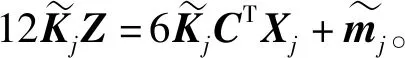
1.4 基本方程

2 转角法计算框架水平位移、内力过程

2.1 节点转角计算

图1 楼层加权转角的计算

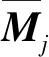
X的计算与Xj的相同，在此不再累述。

2.2 楼层水平位移计算

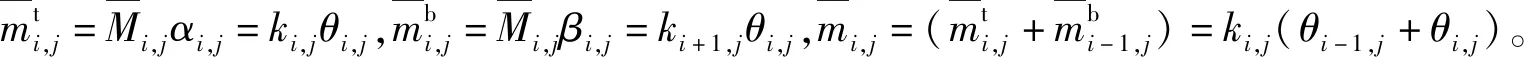
2.3 梁、柱端弯矩计算

算出节点转角和楼层水平位移后，根据梁端弯矩表达式、柱端弯矩表达式可得梁、柱端初始弯矩，把初始弯矩看成是固端弯矩，采用经典的力矩分配法可得梁、柱端弯矩。

3 算例分析

图2为3层框架结构的平面及立面示意图，该算例是D值法分析框架结构内力的经典算例[8]。算例中的结构受横向水平力作用时，全部5榀框架参与受力。图2b中给出了楼层标高处的总水平力，柱边、梁上的数值为每根梁、柱线刚度相对值，柱边、梁下带圈的数值表示单榀框架的梁、柱编号。采用楼层转角方法，边柱和中柱分别计算加权转角，由加权转角、楼层剪力可得楼层层间水平位移和楼层水平位移，计算结果和误差见表1。由表1可看出，虽然楼层转角法计算得出的节点转角与有限元解误差较大，但是楼层水平位移与有限元解误差很小，最大误差不到1%，远优于D值法。

图2 算例框架结构的平、立面示意

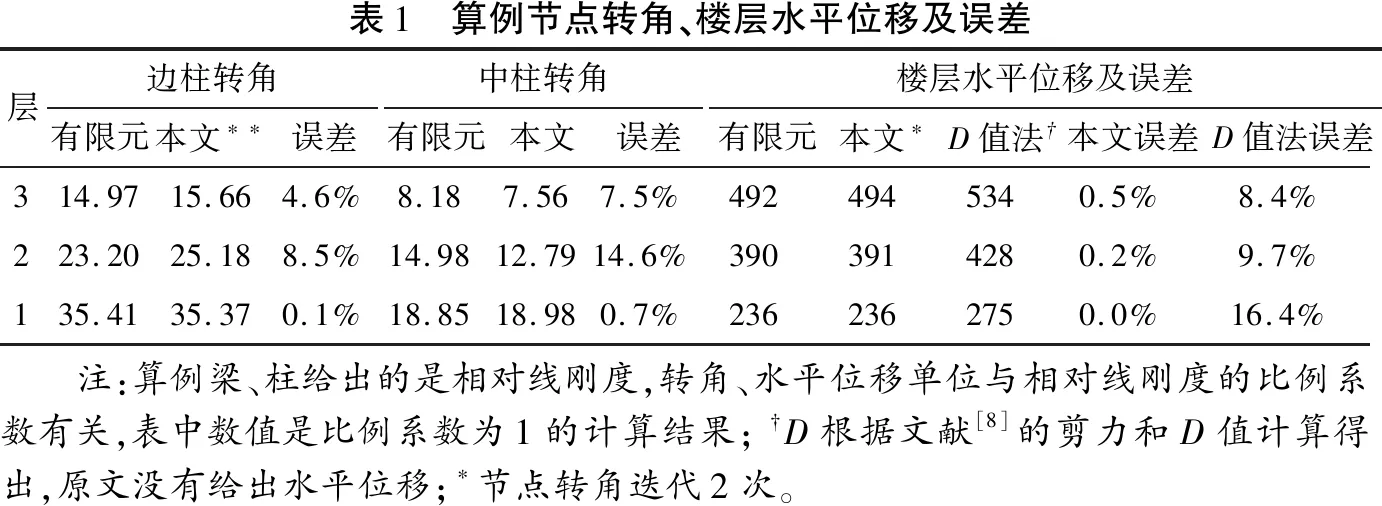
表1 算例节点转角、楼层水平位移及误差层边柱转角有限元本文∗∗误差中柱转角有限元本文误差楼层水平位移及误差有限元本文∗D值法†本文误差D值法误差314.9715.664.6%8.187.567.5%4924945340.5%8.4%223.2025.188.5%14.9812.7914.6%3903914280.2%9.7%135.4135.370.1%18.8518.980.7%2362362750.0%16.4% 注:算例梁、柱给出的是相对线刚度,转角、水平位移单位与相对线刚度的比例系数有关,表中数值是比例系数为1的计算结果;†D根据文献[8]的剪力和D值计算得出,原文没有给出水平位移;∗节点转角迭代2次。

由节点转角和楼层水平位移，可得梁、柱端初始弯矩，把初始弯矩看成梁、柱端固端弯矩，不平衡弯矩分配两次的结果见表2。梁、柱端弯矩最大误差出现在顶层中柱底端弯矩，为1.7%，除此外顶层中柱顶端弯矩和此节点梁端弯矩误差为1.6%。D值法的解最大误差出现在柱②底端弯矩，误差为18.2%；误差不小于10%的梁、柱端弯矩有7个，约占18个杆端弯矩的39%。可见本文方法计算框架结构梁、柱端弯矩具有明显的优势。

把同楼层的所有柱看成整体求解可得1～3层的节点转角分别为27.41、18.96和11.49，楼层的水平位移分别为230、378和475，误差分别为2.5%、3.3%和3.5%，比D值法计算的楼层水平位移精度高，不及单根柱计算的楼层水平位移精度，优势是计算一次梁、柱节点转角。

4 结论

提出了一种求解水平荷载作用下框架结构梁、柱端弯矩的近似方法，方法采用迭代计算节点的加权转角(量纲与弯矩相同)，计算过程与弯矩分配法求解悬臂梁的杆端弯矩类似；算出所有柱的节点转角后，计算楼层水平位移，根据转角位移方程计算杆端弯矩(类似力矩分配法的固端弯矩)，然后利用弯矩分配法计算梁、柱端弯矩。本文方法，也可把所有柱看成一个整体，计算柱的节点转角，算例表明计算结果比D值法的计算精度高，不及本文方法柱分开计算的精度高，优势是只计算一次梁、柱节点转角。算例的计算结果表明，楼层转角法比常用的手算方法计算精度高，求解过程避免了查表，是一种计算精度高的近似方法。

表2 算例梁、柱端弯矩及误差单元柱下端或梁左端弯矩/(kN·m)有限元本文∗D值法弯矩误差/%本文D值法柱上端或梁右端弯矩/(kN·m)有限元本文D值法弯矩误差/%本文D值法①195.1195.4208.30.26.8138.4138.6126.50.18.6②76.877.390.80.718.2101.2101.6106.60.45.3③46.246.852.71.314.161.061.763.21.13.6④221.6221.0226.20.32.1191.4190.8184.70.33.5⑤159.5160.9143.60.910.0167.2168.3143.60.714.1⑥88.089.585.21.73.2100.2101.885.21.615.0⑦215.2215.9217.30.31.0175.4175.8164.10.26.4⑧147.3148.5159.30.88.1127.6128.9114.41.010.3⑨61.061.763.21.13.650.150.942.61.615.0 注:表中梁、柱端弯矩是根据转角位移平衡方程计算的端弯矩,节点不平衡弯矩分配两次、弯矩传递一次的结果。