具身认知视角下面向幼儿的计算思维游戏化教学模型构建与应用*

2022-12-27李艳燕胡婉青黄睿妍

现代教育技术 2022年12期

李艳燕胡婉青黄睿妍傅骞

李艳燕胡婉青黄睿妍傅骞[通讯作者]

（北京师范大学教育技术学院，北京 100875）

如今，随着计算思维教育的推广，如何发展幼儿的计算思维成为教育工作者面临的教学困境。为此，文章充分考虑了幼儿的认知特点，并基于加里斯等提出的游戏化学习模型，从具身认知的视角出发梳理了游戏圈中幼儿和学习工具、教师的关系，构建了EC-CT教学模型来促进幼儿的计算思维和学习动机，该教学模型解释了幼儿是如何在身体和环境的交互中学习计算思维的，并描述了教师在其中发挥的作用。随后，文章基于该教学模型开发了高具身性的实体编程工具和低具身性的纸笔工具，设计了配套的学习活动，并招募了被试参与活动。研究发现，基于该教学模型设计的两套工具和活动都能够有效地培养幼儿的计算思维和激发幼儿的学习动机，并且高具身性工具的促进效果更加明显。文章旨在为幼儿计算思维的培养提供理论参考和实践支持。

计算思维；教学模型；幼儿；具身认知

一问题提出

2006年，周以真教授提出了“计算思维”（Computational Thinking，CT）这一概念，并指出未来计算思维将和阅读、写作、算术一样成为每个人都应该掌握的能力[1]。此后，世界各国开始陆续将计算思维纳入K12正式教育中。到目前为止，全球的教育工作者已经达成共识：计算思维已成为21世纪人才的基本素养，应该在所有学段（从学前到高等教育阶段）开展相关的教育活动[2]。

尽管研究者指出从幼儿阶段（3～8岁）就开始培养计算思维非常重要，但是目前关注幼儿计算思维发展的研究相对较少[3]。一方面，幼儿尚不具备成熟的算术和抽象推理等技能，不能完全脱离物理表征去理解抽象的概念和逻辑[4]，这就给针对幼儿的计算思维教学设计带来了巨大的挑战。另一方面，尽管一些研究者开发了针对幼儿的计算思维教学活动和工具[5][6]，但是并没有关注如何将这些活动和工具系统性地组织起来，导致相关教学活动的开展普遍缺乏理论指导。对此，研究者指出具身认知观点能够给针对幼儿的计算思维教学设计带来启发[7]。具身认知（Embodied Cognition，EC）是认知科学中一类理论的总称，强调身体和环境的交互对于认知的重要性，认为人可以通过感知运动循环发展高级思维[8]，这恰好满足了幼儿依赖物理环境和身体体验学习抽象知识（如计算思维）的需求。与此同时，研究者指出在基于具身认知理论设计的教学活动中融入游戏元素，可以帮助幼儿更好地投入到学习过程中，从而提升教学效果[9]。

基于此，本研究充分考虑了幼儿的认知特点，从具身认知的视角出发，提出了一个针对幼儿的计算思维游戏化教学模型——EC-CT教学模型。随后，本研究基于该教学模型设计了针对幼儿的两套学习工具及其相关活动，并验证该教学模型的有效性，以期为今后幼儿计算思维的培养提供理论参考和实践支持。

二文献综述

1 计算思维的游戏化教学

研究者提出了各种各样的计算思维教学模型来指导教师开展计算思维教学，并通过实证研究验证了模型的有效性[10][11]。但是，已有的计算思维教学模型主要针对中学生和大学生，较少面向幼儿。另外，现有计算思维教学模型中的关键载体主要是文本编程或图形化编程，但这两种编程形式对于幼儿的认知负荷都较大，并且该阶段的孩子正处于视力发展的关键期，与电脑、平板或手机等电子屏幕有过多的接触，也不利于其视力健康[12]。由此可见，目前亟需建立考虑到幼儿特点的计算思维教学模型，为一线教师提供幼儿计算思维教学的理论指导。

虽然目前没有针对幼儿的计算思维教学模型，但研究者已经探索出一些有效培养幼儿计算思维的方式，目前主要有两种：一种是让幼儿按照包含运动提示的预定义序列实施物理表演[13]，比如有研究者设计了角色扮演游戏，让幼儿扮演机器人，按照教师或者同伴的方向指令进行运动[14]。另一种是让幼儿控制一个外部的物理对象或虚拟角色发生运动[15]，实体编程工具就是这种形式的典型代表，比如较多研究者使用了实体编程工具Beebot，幼儿通过按键给Beebot下发指令，控制Beebot在地图上进行移动并最终抵达目的地[16]；还有研究者设计了包含竞争和奖励等机制的纸牌游戏“Code Ocean”，幼儿需要使用指令卡牌来控制海盗船进行移动[17]。

这些研究都证明了融入游戏元素并重视身体体验的活动确实能够有效地激发幼儿的学习动机并促进幼儿的计算思维，但这些研究并没有解释为什么这些基于身体体验的活动能够培养计算思维[18]。研究者呼吁未来需要更多的研究来关注这些学习工具和活动是如何组织在一起促进计算思维的，并且这些活动还需要更扎实的理论基础[19]。

2 具身认知视角下的计算思维教学

20世纪80年代以前，主流的认知理论认为认知是一个抽象的信息处理过程，与身体的感知与行动是剥离开的[20]。与此不同的是，具身认知理论强调身体和环境的交互在认知中所起的作用，认为人类的认知过程是根植于人与环境的物理交互的[21]。具身认知领域的研究者认为，当个体在环境中活动时，行动影响知觉，知觉又会影响未来行动，未来行动接着又决定新的知觉，如此往复从而形成“感知—运动”循环[22]。

身体与物理世界的交互活动能够帮助学习者掌握抽象概念[23]，而具身认知强调动觉经验与抽象概念的联系，因此研究者指出创建学习环境让学习者自然地参与到映射抽象概念的身体活动中是非常重要的[24]。同时，具身认知观点与过去专家在幼儿教学中重视幼儿身体动作的理念也是一致的[25]。但是，目前少有研究者从具身认知的角度出发设计幼儿计算思维教学并验证其效果。有研究者尝试从具身认知的视角为幼儿设计了计算思维课程，探索幼儿在活动中参考系统的转变规律，但是该研究并没有验证幼儿的计算思维是否有所发展[26]。此外，还有一项研究从具身认知的角度出发设计了低具身性和高具身性的活动帮助幼儿学习数学，发现高具身性的活动能够帮助幼儿更好地理解计算观点[27]。尽管该研究并没有聚焦于幼儿计算思维的培养，但是其发现证明了基于具身认知理论的教学活动在培养幼儿计算思维方面的潜力。

总的来说，目前亟需适合幼儿的计算思维教学模型。过去的研究也说明了具身认知理论与幼儿计算思维教学的适切性，并充分证明了融入游戏化要素对于培养幼儿计算思维的积极作用。因此，本研究基于具身认知理论，以幼儿为对象构建了计算思维游戏化教学模型，随后根据模型设计了学习活动和工具，并验证了其能否有效促进幼儿计算思维的发展。

三 EC-CT教学模型的构建

1 理论基础

①具身设计。具身设计（Embodied Design）是指应用具身认知理论来设计学习环境。Abrahamson等[28]提出了包含活动、资源和促进三个方面的具身设计原则：在活动方面，应充分地调动学习者的身体经验并按照由易到难的顺序进行组织；在资源方面，应创设学习环境使学习者通过物理或心理动作发生感知运动循环，并帮助学习者发展出新的感知—运动模式，从而更好地控制对象，达成更复杂的目标；在促进方面，需要为学习者设计脚手架来制定目标知识的隐喻。此外，还需要创建学习环境为学习者提供物理的实时反馈，并且由教师引导学习者总结在交互过程中形成的策略。具身设计原则指导本研究建立了幼儿与学习工具的具身交互机制，并在设计学习工具和教学活动方面提供了理论参考。

②游戏化学习。游戏能够激发人们的内在动机[29]，故进行教学设计时常引入竞争、奖励等游戏化要素来激发学习者学习。Garris[30]认为大多数教育游戏存在一种隐性学习模式，可将其总结为输入、游戏圈以及输出三个阶段，并以此构建了设计游戏化教学项目的模型：首先在输入阶段，要确定教学项目涉及的教学内容以及需要结合的游戏特征。然后，输入会触发一个被称为游戏圈的循环，游戏圈中包括用户的判断或反应（如享受或兴趣）、用户行为（如更大的持久性或任务时间）以及进一步的系统反馈。如果能够成功地将教学内容与适当的游戏功能相匹配，就能形成自我激励的游戏循环。最后，在输出阶段，用户通过参与游戏可以达到教学目标，形成特定的学习成果。参考设计游戏化教学的这三个核心阶段，本研究对教学模型进行了设计。

2 模型构建

在计算思维教学的背景下，基于上述“输入—游戏圈—输出”游戏化教学模型，本研究从具身认知的视角重新梳理了游戏圈中用户和系统的关系，即幼儿和学习工具、教师的关系。具体来说，幼儿通过控制学习工具和感知学习工具的反馈形成感知运动循环，而教师需要支持幼儿与工具的交互（如图1所示）。具身认知观点的引入使该模型能够更深刻地解释幼儿是如何在身体和环境的交互中学习计算思维的，以及教师在其中起到的作用。

①输入。模型的输入阶段包括课程内容和游戏特征，这里的课程内容就是计算思维的三个维度——概念、实践和观念，这里的游戏特征主要包括任务、竞争和奖励，这些游戏化元素已被证明能够帮助幼儿发展计算思维[31]。接着，再通过基于问题的教学模式来设计以计算思维三维框架为核心内容、以游戏化为外在形式的学习活动，也就是图1中的游戏圈。并且，随着游戏圈中幼儿通过和学习工具的交互不断发展计算思维并提升学习动机，输出的结果也会进一步影响课程内容和游戏特征的设计。

②游戏圈。游戏圈的核心在于幼儿通过“感知—运动”循环与学习工具发生交互，从而发展计算思维。输入的教学内容映射在幼儿的“感知—运动”循环中，而输入的游戏特征激励幼儿投入到“感知—运动”循环中。具体来说，首先幼儿通过感官感知到学习工具提供的信息，基于这些信息，幼儿需要操作学习工具，构建问题解决方案。在适当的时候，幼儿会自发地验证问题解决方案，这时学习工具会将可感知到的信息反馈给幼儿，幼儿在感知到反馈后又会操纵学习工具，如此循环直到真正地解决问题。

在幼儿自主探索解决问题的过程中，教师作为支架来支持幼儿与学习工具之间的具身交互。首先，教师会引导幼儿解读学习工具的反馈，帮助幼儿更好地利用学习工具的反馈信息。然后，教师需要营造游戏的氛围，激发幼儿的学习动机，比如提醒先完成任务就可以获得更多的分数等。与此同时，教师还要采取措施降低幼儿在阅读和记忆上的负荷，使其将自己的认知资源集中在解决问题上，比如可以结合多媒体资源创设情景，提供实体卡片帮助幼儿记住问题信息。

③输出。该模型的预期输出结果主要是计算思维的发展和学习动机的提升。在计算思维方面，幼儿在和学习工具交互的过程中，能够通过“感知—运动”循环理解计算思维的基本概念。当通过不断的“感知—反馈”循环形成一定的“感知—运动”模式时，幼儿也就掌握了对应的计算思维实践。同时，幼儿也会在这个过程中形成对计算思维的态度和观点。在学习动机方面，当幼儿进入这种“感知—运动”循环中时，其注意力将会自然而然地得以维持。此外，竞争、奖励机制带来的胜负感以及完成任务带来的成就感，也会激发幼儿的内在学习动机。

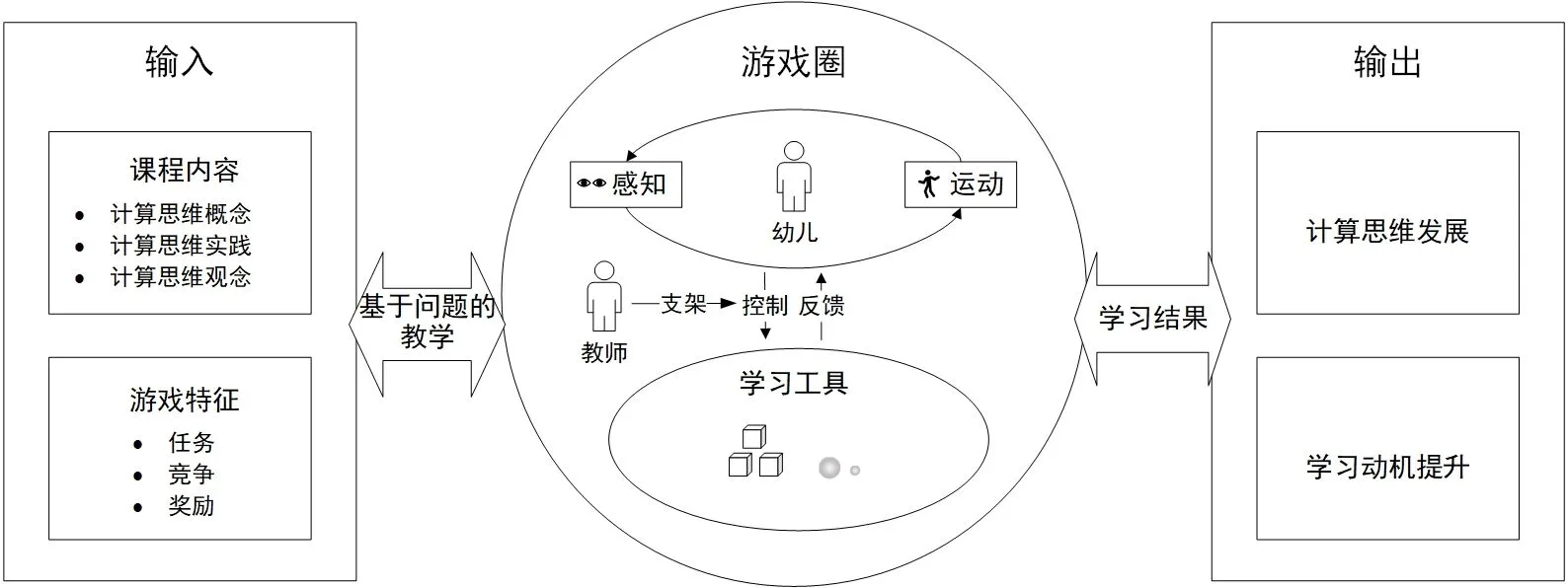
图1 具身认知视角下的计算思维游戏化教学模型（EC-CT教学模型）

四研究设计

为探究EC-CT模型的应用效果，本研究设计了具有高低具身性的两套学习工具及其活动（其中高具身性工具提供了更多的动觉体验），并探索了在参与两种活动前后，幼儿的计算思维与学习动机是否有存在差异，以及两种活动在幼儿计算思维的促进和学习动机的提升上是否存在差异。

1 研究对象及流程

本研究采用方便抽样的方法，于2021年7月招募了45名6～8岁的幼儿参与实验，他们被随机分配到高具身性组（28名）和低具身性组（17名）。其中高具身性组的平均年龄为7.1岁，低具身性组的平均年龄为7.2岁，所有被试均未学习过计算思维的相关课程。整个活动持续约110分钟，在开始时被试需要在15分钟内完成计算思维前测。此后，被试参与10分钟的培训活动，熟悉各自组中学习工具的使用规则。接着，被试在5分钟内完成学习动机前测。随后，教师引导被试在60分钟内进行4个活动，两组的学习情景和内容完全一致，并且都由同一个教师开展教学，但是使用的学习工具不同。最后，被试在20分钟内完成学习动机和计算思维的后测。

2 学习工具设计

基于EC-CT教学模型，本研究设计了CodeWay实体编程工具和CodeWay纸笔工具。高具身性组使用CodeWay实体编程工具，它由一系列具有特定功能的积木块以及大球、小球组成。在实验中，高具身性组的幼儿需要利用功能不同的CodeWay积木块搭建出一条通路，让小球在重力的作用下从起点走到终点，如图2（a）所示。每个小球滚动的过程就是算法执行的过程，而搭建通路的过程则是设计算法、解决问题的过程。表1呈现了实体编程工具与计算思维概念的映射关系。被试摆放好积木块后投入小球，会通过视觉、声音等感知到小球的滚动轨迹，如果小球的滚动轨迹不符合预期，被试将再次调动身体控制积木块。在这样的感知—运动循环中，被试将逐渐理解小球动作、积木块颜色所映射的计算思维概念。当通过不断的“感知—反馈”循环形成了一定的“感知—运动”模式时，被试也就掌握了对应的计算思维实践。

低具身性组使用了CodeWay纸笔工具，如图2（b）所示。该纸笔工具的使用规则与实体编程工具的使用规则基本一致，核心区别在于实体编程工具的使用流程是被试通过搭建积木让小球发生运动从而解决问题，而纸笔工具的使用流程是被试在方格地图上绘制具有特定含义的图标来解决问题。高具身性组的积木块与低具身性组使用的图标是一一对应的，所映射的计算思维概念也是一致的。低具身性组的被试并没有实体的小球作为一个具身的思考对象，对于该组的被试来说，其对于小球的认知是离线的，“感知—运动”循环存在于其想象中。

图2 高低具身性组使用的学习工具

图3 学生的问题解决方案

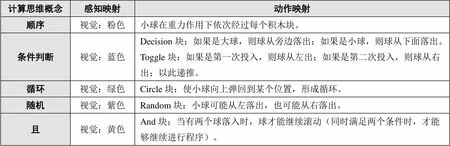
表1 实体编程工具与计算思维概念的映射关系

3 学习活动设计

在60分钟的学习活动中，两个组的被试都将完成四个任务，且根据具身设计原则，任务的难度设置逐渐增加。在学习活动开始前，教师建立了包含奖励机制和竞争机制的游戏规则。每个学习活动的流程都是在基于问题的教学模式指导下设计的，主要包含情景引入、问题解决、评价与反思三个阶段。表2呈现了学习活动内容，图3学生针对呈现了“挑选试衣间”这一任务的问题解决方案。

表2 学习活动内容

4 数据收集与分析

在数据收集方面，本研究从2018年和2019年国际Bebras比赛6～8岁类别的题目中选择了9道进行计算思维测试，这些题目按照难度从低到高进行排序。基于前测题目，研究团队设计了与其难度相同的不同版本作为后测题目。由于幼儿阅读能力尚不成熟，在测试环节每名幼儿都有一名助教帮忙阅读题目。在学习动机的测量方面，本研究使用Loorbach等[32]经过修改和验证的学习动机量表，包含了注意力、相关性、信心和满意度四个维度，具有较好的信度（Cronbach α=0.92）。该量表采用李克特量表计分，取值为1（非常不同意）～5（非常同意）。在数据分析方面，本研究使用Wilcoxon方法对比在参与学习活动前后，被试的计算思维以及学习动机是否存在显著差异；同时使用曼惠特尼U检验，对比高低具身性组计算思维和学习动机的差异。

五结果与讨论

1 计算思维水平

本研究发现，两组被试的计算思维平均分在参与学习活动之后都得到了提升，具体计算思维测试结果如表3所示。使用Wilcoxon方法检验被试后测和前测的分数，发现两组被试的计算思维后测分数都显著高于前测分数，这说明本研究中基于EC-CT教学模型设计的两套学习工具及其相关活动都能够有效促进幼儿的计算思维。尽管使用曼惠特尼U检验发现高低具身性组在前测和后测上均没有统计学意义上的显著差异（U=232.50，=0.90；U=204.00，=0.41），但是从平均分来看，高具身性组被试在前测时分数低于低具身性组，而后测时超过了低具身性组，这可能说明高具身性的学习工具更有益于幼儿发展计算思维。之前的研究也发现，高具身性活动更能促进幼儿的数学理解和编程技能[33]。

另外，本研究还发现，在高具身性组中，尽管教师没有讲授如何进行调试，但部分被试在使用实体编程工具时仍然自发地参与了调试的过程。这些发现都证明了本研究中实体编程工具的优势：与Beebot类似的教育机器人相比[34]，该工具提供了可视化的指令，降低了幼儿记忆的负荷；与一些桌面游戏[35]以及本研究中的纸笔工具相比，该工具通过小球的运动提供了反馈，使幼儿能够自然地参与到感知运动循环中。而实体编程工具的优势，正反映了本研究中EC-CT教学模型的优势。

表3 计算思维测试结果

注：*＜0.05，**＜0.01。

2 学习动机水平

使用Wilcoxon方法分别检验两个组的学习动机，具体测试结果如表4所示，可以看出：高具身性组的学习动机后测分数显著高于前测分数（z=-3.75，＜0.01），低具身性组则无显著差异（如表4所示）。从学习动机各个子维度上来看，高具身性组在注意力、相关性和满意度上都得到了显著提升（z=-2.79，＜0.01；z=-2.69，＜0.01；z=-2.02，=0.04），并且注意力这一维度提升的分值是最大的。尽管使用曼惠特尼U检验发现高低具身性组在计算思维前测、后测中均无显著差异（U=218.00，=0.64；U=183.50，=0.19），但在前后测中，高具身性组的学习动机平均分都高于低具身性组，这说明高具身性组的学习工具更能吸引幼儿的注意力，激发幼儿的兴趣。

表4 学习动机测试结果

奥尔莫等[36]发现幼儿在使用了类似的低具身性工具进行学习后，学习动机呈现下降趋势。但是本研究中高具身性组的学习动机却得到了提升，这可能是因为本研究设计的实体编程工具使被试在外显的“感知—运动”循环中能够自然而然地维持注意力，以激发他们的兴趣。相较而言，被试在使用低具身性的纸笔工具时，“感知—运动”循环则是内隐的，其无法直接从学习工具上得到显性反馈。这在一定程度上说明了高具身性的实体编程工具比起低具身性的纸笔工具更能充分地吸引幼儿，使其在学习中保持兴趣和专注。

六总结

本研究从具身认知视角提出了面向幼儿的计算思维游戏化教学模型，强调了幼儿需要通过“感知—运动”循环来与学习环境发生交互，从而发展计算思维。本研究发现，基于该模型设计的两套工具和活动都能够有效地培养幼儿的计算思维并激发其学习动机，并且高具身性的实体编程工具的促进效果更加明显——这些发现证明了EC-CT模型的优势与有效性。本研究对幼儿的计算思维教学具有两方面的启示：①在学习环境设计方面，要充分考虑到幼儿依赖物理环境理解抽象概念的特点，并建立及时且具身的反馈机制，使幼儿能够自然地参与到“感知—运动”循环中；②在学习活动设计方面，需要围绕幼儿真实生活情景中的问题，将活动按照从简单到困难进行排序，并且在活动中融入合适的游戏化元素，比如奖励、竞争等来激发幼儿的学习动机。本研究也存在一定的局限性，比如实验时间较短，只证明了基于EC-CT教学模型的两套学习工具及其相关活动在短期的效果，并且由于疫情原因招募到的被试较少。未来研究可以进一步扩大样本量，开展长期实验并且深入探索幼儿学习计算思维的过程。

[1]Wing J M. Computational thinking[J]. Communications of the ACM, 2006,(3):33-35.

[2][7][19]Huang W, Looi C K. A critical review of literature on “unplugged” pedagogies in K-12 computer science and computational thinking education[J]. Computer Science Education, 2021,(1):83-111.

[3][16]Angeli C, Valanides N. Developing young children’s computational thinking with educational robotics: An interaction effect between gender and scaffolding strategy[J]. Computers in Human Behavior, 2020,(105):105954.

[4]Beilin H. Developmental stages and developmental processes[A]. Measurement and Piaget[C]. New York: McGraw-Hill, 1971:172-196.

[5][36]del Olmo-Muñoz J, Cózar-Gutiérrez R, González-Calero J A. Computational thinking through unplugged activities in early years of Primary Education[J]. Computers & Education, 2020,150:103832.

[6][14][34]Saxena A, Lo C K, Hew K F, et al. Designing unplugged and plugged activities to cultivate computational thinking: An exploratory study in early childhood education[J]. The Asia-Pacific Education Researcher, 2020,(1):55-66.

[8][21][24][28]Abrahamson D, Lindgren R. Embodiment and embodied design[A]. The Cambridge Handbook of the Learning Sciences[C]. Cambridge: Cambridge University Press, 2014:358-376.

[9]Er S. Using total physical response method in early childhood foreign language teaching environments[J]. Procedia-Social and Behavioral Sciences, 2019,(21):1766-1768.

[10]丁世强,王平升,赵可云,等.面向计算思维能力发展的项目式教学研究[J].现代教育技术,2020,(9):49-55.

[11]陈兴冶,马颖莹,杨伊.面向计算思维发展的深度学习模型建构——以可视化编程教学为例[J].电化教育研究,2021,(5):94-100、121.

[12]王佑镁,宛平,南希烜,等.实体编程促进计算思维发展:工具与策略[J].中国电化教育,2021,(8):92-98.

[13][15][22]Fadjo C L. Developing computational thinking through grounded embodied cognition[D]. New York: Columbia University, 2012:15-48

[17][31][35]Chen K Z, Chi H H. Novice young board-game players’ experience about computational thinking[J]. Interactive Learning Environments, 2022,(8):1375-1387.

[18]Manches A, Mckenna P E, Rajendran G, et al. Identifying embodied metaphors for computing education[J]. Computers in Human Behavior, 2020,105:105859.

[20][23]Barsalou L. Grounded cognition[J]. Annual Review of Psychology, 2008,(1):617-645.

[25]Asher J J. Children learning another language: A developmental hypothesis[J]. Child Development, 1977,(3):40-1048.

[26]Clarke-Midura J, Kozlowski J S, Shumway J F, et al. How young children engage in and shift between reference frames when playing with coding toys[J]. International Journal of Child-Computer Interaction, 2021,28:100250.

[27][33]Sung W, Ahn J, Black J B. Introducing computational thinking to young learners: Practicing computational perspectives through embodiment in mathematics education[J]. Technology, Knowledge and Learning, 2017,(3):443-463.

[29]Malone T W, Lepper M R. Making learning fun: A taxonomy of intrinsic motivations for learning[A]. Aptitude, Learning, and Instruction[C]. London: Routledge, 2021:223-254.

[30]Garris R, Ahlers R, Driskell J E. Games, motivation, and learning: A research and practice model[J]. Simulation & Gaming, 2002,(4):441-467.

[32]Loorbach N, Peters O, Karreman J, et al. Validation of the instructional materials motivation survey (IMMS) in a self-directed instructional setting aimed at working with technology[J]. British Journal of Educational Technology, 2015,(1):204-218.

The Construction and Application of Computational Thinking Gamification Teaching Model for Young Children from the Perspective of Embodied Cognition

LI Yan-yan HU Wan-qing HUANG Rui-yan FU Qian[Corresponding Author]

At present, with the promotion of computational thinking education, how to develop young children’s computational thinking has become a teaching dilemma faced by educators. Therefore, fully considering young children’s cognitive characteristics, this paper combed the relationship among children, learning tools and teachers in the game circle from the perspective of embodied cognition, and constructed an ET-CT (Embodied Cognition—Computational Thinking) teaching model based on the gamification learning model proposed by Garris et al. This model explained how young children learned computational thinking by the interaction between the body and the environment, and described the role teachers played in it. Furthermore, based on the teaching model, a high-embodied entity programming tool and a low-embodied pen and paper tool were developed for young children, and supporting learning activities were designed, and the subjects were recruited to participate in these activities. It was found that the two sets of tools and activities designed based on this model could effectively cultivate young children’s computational thinking and stimulate their learning motivation, and the effect of the high-embodied tool was more obvious. Through the research, this paper was aimed to provide theoretical reference and practical support for the cultivation of young children’s computational thinking in the future.

computational thinking; teaching model; young children; embodied cognition