数学在线样例学习中的工作记忆资源损耗效应

林洪新，马 荃，管 晓，杜雪娇

数学在线样例学习中的工作记忆资源损耗效应

林洪新，马 荃，管 晓，杜雪娇

（鲁东大学 教育科学学院，山东 烟台 264011）

模块样例与模块化样例是数学题的“一题两解”．以往研究发现模块化样例学习的效果好于模块样例，但附加解释的模块与模块化样例学习的效果与机制尚不明确．研究考查了不同样例形式与解释推送策略下128名三年级小学生的数学在线学习效果．结果显示：模块样例与模块化样例形式下小学生的工作记忆容量没有差异，模块化样例形式下的近迁移成绩高于模块样例，未表现出工作记忆资源损耗效应；与自由选择解释相比，固定推送解释下小学生的工作记忆容量更低，近迁移成绩更差，表现出工作记忆资源损耗效应．这表明数学在线样例学习中可优先呈现模块化样例，允许小学生自由选择解释，进而降低工作记忆资源损耗，提高学习效果．

在线样例学习；工作记忆资源损耗效应；小学生；解释；推送策略

1 问题提出

知识是个体生存与发展的必要条件．学校教育是个体获得系统知识的重要途径，而教学材料设计是影响学校教育效果的主要客观因素．澳大利亚心理学家John Sweller自20世纪70年代就开始关注教学材料设计，并通过实验研究发现与问题解决形式相比，样例学习是知识习得的更有效的教学材料设计形式[1]．所谓样例（worked example），指以逐步呈现解题步骤的形式为个体提供学习问题解决方法的例题．样例学习（worked example learning）是个体在已有知识的基础上，通过阅读和思考样例，领会问题解决的新知识并掌握其应用的过程．随后，他又提出认知负荷理论（Cogni- tive Load Theory），用于解释样例学习形式有效的原因[2]．

随着样例与样例学习概念的提出，研究者们设计出了不同形式的样例并验证其有效性．其中，模块样例（molar worked example）与模块化样例（modular worked example）是2004年Gerjets、Scheiter和Kleinbeck正式提出的两种样例形式．所谓模块样例是一种使用整体解题方案去解决某类问题的样例；模块化样例是将整体解题方案划分为几个可以被单独理解和处理的解题步骤组（或小事件）的样例[3]．例如，小明和小红分别从甲、乙两地相对而行，已知小明以每小时35千米的速度开车从甲地出发，小红以每小时15千米的速度骑车从乙地出发，经过2小时两人相遇，问甲、乙两地相距多少千米？如果采用模块样例，其计算过程是将小明与小红的速度相加后乘以时间得出总路程；如果采用模块化样例，其计算过程是先计算小明开车走的路程，再计算小红骑车走的路程，最后将小明与小红走的路程相加得出总路程．因此，模块样例往往是整体式问题解题思路，包括识别抽象任务类别、应用具体公式、代入数值和计算4个主要步骤；而模块化样例主要采用分解式问题解题思路，即将整个问题划分成几个小事件，然后依次解决每个小事件，最终解决问题．

模块样例与模块化样例学习研究起源于子目标编码研究．Catrambone以大学生为被试，首先分组学习采用方程（模块）或子目标编码（模块化）解决概率计算问题的样例，然后参加迁移测验．结果发现，子目标编码样例形式下被试的近迁移与远迁移成绩均显著好于方程样例形式下的成绩[4]．随后，研究者们细化了子目标编码形式．一种是分解任务形式（part-whole sequencing），即先将复杂任务分解为多个简单任务，当被试掌握若干简单任务之后再学习复杂任务[5–6]．另一种是模块化样例形式，即根据结构或意义特征将样例的解题步骤划分为几个小事件（或步骤组），促进被试对样例解题步骤组的理解与记忆，进而提高学习效果[7–11]．

Gerjets、Scheiter和Kleinbeck对比了概率计算问题的模块与模块化样例学习效果，结果发现模块化样例形式下被试的问题解决时间与成绩均优于模块样例形式[8]．为了进一步验证模块化样例在解决其它概率问题上是否同样具有优越性，Gerjets、Scheiter和Catrambone在实验中选取了6个不同类别概率问题，每类问题设计2个样例，共12个样例，被试按随机顺序学习6类样例．结果发现，在6个不同类别概率问题上，模块化样例形式下被试的迁移成绩均显著高于模块样例形式[8]．随后，他们在研究中进一步测量了被试的先验知识水平、样例学习时间和认知负荷水平．结果发现无论被试的先验知识水平高低，与模块样例形式相比，模块化样例形式下被试的学习时间更短，认知负荷水平更低，测验成绩更高[9]．他们认为新手在模块样例学习中会消耗更多的认知资源，降低学习效果[10]．Calhoun以护理教育专业博士研究生与本科生的信息素养学习为研究内容，结果发现采用多媒体与模块化样例相结合的方法能够显著提高被试在多项选择题与界定含混问题解决上的成绩[11]．由此可见，与模块样例学习相比，数学概率问题等内容的模块化样例学习具有一定的优势．

附加解释样例是一种常见的样例设计形式，但解释能否提高模块与模块化样例学习的效果还存在争议[12–14]．Renkl研究发现，在学习概率计算问题中，附加解释模块样例下被试的迁移成绩显著高于无附加解释模块样例[12]．Gerjets、Scheiter和Catrambone在实验中比较了不同解释水平下模块样例与模块化样例的学习效果．解释水平包括无解释、中等解释与详细解释3种水平．无解释指样例中没有附加任何解释；中等解释指给出样例中每个解题步骤的计算过程和数值代入方面的信息，没有给出具体理由；详细解释呈现了每个解题步骤的详细理由．实验记录了被试的样例学习时间、认知负荷水平、迁移测验时间与正确率．结果发现，与无解释和中等解释水平相比，详细解释水平下被试的模块与模块化样例学习效果较差，即详细解释降低了模块与模块化样例学习的效果[9]．由此可见，以往关于附加解释能否提高模块和模块化样例学习效果的研究较少，结果也不尽一致．

综上所述，以往关于模块与模块化样例的研究主要集中在两种样例学习效果的比较与附加解释的作用上．研究发现模块化样例学习的效果要好于模块样例，这可能是因为模块样例呈现的是整体式问题解题思路，被试需要在工作记忆中同时加工较多元素，从而没有足够的认知资源对样例结构特征进行深入思考；而模块化样例的解题步骤组是建立在小事件基础之上，这会减轻被试的认知负荷，同时加强他们对样例结构的理解与记忆．但是，以往两种样例研究的内容主要集中在概率计算问题上，研究对象局限于大学生及以上，中小学生的认知能力尚不完善，且其数学知识学习中普遍存在“一题两解”情况，扩大样例学习内容与对象有助于验证模块化样例学习的适用范围．

以往研究发现附加解释的模块与模块化样例学习的效果还存在不一致之处．Gerjets等人研究发现，附加详细解释会降低模块与模块化样例学习的效果[9]，但Renkl研究发现附加解释提高了模块样例学习的效果[12]．这可能是因为在Gerjets等人的研究中，详细解释水平下呈现了每个样例的每个解题步骤的详细理由，这些过多的解释会导致被试将注意力投入到重复信息上，消耗他们有限的认知资源，降低学习效果[13]．而Renkl研究中的样例数量较少，呈现的是一个整体解释，这些解释则可以帮助被试弥补知识上的空缺，理解样例中所蕴含的原理与规则[14]，因此学习效果较好．由此可见，必要的解释可以提高被试对样例的理解，而过多的解释则会增加他们的认知负荷．那么如何呈现解释更有效？林洪新、杨帅峰和杜雪娇研究发现，场独立型小学生数学在线样例学习时更适合自由选择渐减步骤样例，场依存型小学生更适合固定推送附加解释样例[15]．Chen、Mitrovic和Matthews研究发现，在线学习中学生主动选择学习内容会显著激发他们的积极性，进而提高学习效果[16]．借鉴以往研究结果，研究提出并考察两种解释推送策略：一种是自由选择解释，即学生根据自己的需要选择是否查阅解释；另一种是固定推送解释，即系统自动呈现解释．为更好地分析两种解释推送策略下小学生数学模块与模块化样例学习的效果，研究还将测量他们在样例学习结束之后的工作记忆容量，以此为指标，比较各组被试的工作记忆资源损耗情况．这是因为工作记忆不是恒定的无限资源，而是可损耗的有限资源[17]．样例学习中的工作记忆容量下降，会导致学生没有足够的工作记忆资源完成随后的测验，降低随后的测验成绩，产生工作记忆资源损耗效应（Working Memory Resource Depletion Effect）[18–19]．基于以上分析，提出研究假设：（1）与模块化样例形式相比，模块样例形式下小学生的工作记忆容量下降，测验成绩降低，表现出工作记忆资源损耗效应；（2）与自由选择解释相比，固定推送解释下小学生的工作记忆容量下降，测验成绩降低，表现出工作记忆资源损耗效应．

2 研究方法

2.1 被试

通过“基础知识测试题”在某市选取三年级小学生128人，男女生各64人，年龄在8.95±0.67岁之间（或平均年龄为8.95岁）．将被试随机分配到模块样例+自由选择解释、模块样例+固定推送解释、模块化样例+自由选择解释、模块化样例+固定推送解释4种条件下，每种条件下32人．

2.2 实验设计

实验采用2（样例形式）×2（解释推送策略）两因素被试间实验设计．样例形式包括模块样例与模块化样例：前者指用整体式解题思路解决“相遇问题”的例题；后者指用小事件分解式解题思路解决“相遇问题”的例题．解释推送策略包括自由选择解释与固定推送解释：前者是在屏幕的右上页面展示“查看解释”与“跳过”两个超链接按钮，被试可以自由选择；后者是在屏幕的相同位置呈现例题的详细解题思路．实验记录被试在样例学习后的认知负荷水平、工作记忆容量与迁移测验成绩．

2.3 实验材料

实验材料包括基础知识测试题、工作记忆容量测验、样例学习材料、认知负荷量表与迁移测验材料．

2.3.1 基础知识测试题

主要用于筛选被试，包括10道题，其中8道题是加减乘除混合运算选择题，1道是“相对而行”概念的选择题，1道是“相遇问题”应用题．

2.3.2 工作记忆容量测验材料

工作记忆容量测验改编自Chen等人的研究[18–19]．该测验已被广泛应用于测量小学生的工作记忆容量，并以此来衡量他们的工作记忆资源损耗．测验由低到高包括4个难度水平，每个难度水平依次由3～6个算式组成，每个难度进行3次试验，因此，测验共包括54道算式．在测验过程中，被试需同时在工作记忆中完成加工与记忆两个任务．在一次试验中，首先向被试呈现第1道算式，要求被试判断算式的计算结果是否正确，并在答题册上相应位置写下答案，同时记住算式的第1个数字，接着呈现第2道算式，要求相同，直至一次试验所有算式呈现结束，要求被试按顺序回忆并写下这次试验中每个算式的第一个数字．实验首先进行两次练习，待练习结束后并且被试听懂和学会了才进入正式的工作记忆容量测验．测验结束后统计被试的回忆成绩，作为工作记忆容量得分．正确回忆1个数字计1分，最高为54分．在测验过程中，每页PPT播放一个算式，播放时间为6秒．

2.3.3 样例学习材料

包括“相遇问题”的模块样例与模块化样例各4道，共8道．模块样例包括“相遇问题”的题面和整体式解题步骤，模块化样例包括“相遇问题”的题面与分解式解题步骤．在固定推送解释下，每道模块或模块化样例的右上角呈现关于样例的详细解题思路，如图1所示；在自由选择解释下，每道模块或模块化样例的右上角呈现“查看解释”和“跳过”两个按钮，被试可以根据自己的理解情况选择点击按钮．样例学习材料采用PPT的形式播放，每页PPT呈现一道例题，如图2所示．

图1 固定推送解释下模块样例学习材料

图2 自由选择解释下模块样例学习材料

2.3.4 认知负荷量表

采用Paas于1992年编制的PAAS认知负荷自评量表，该量表具有较高的信度与效度[20–21]．量表包括心理努力与任务难度2个问题，采用9点计分法，1表示程度最低，9表示程度最高．量表的内部一致性系数=0.85．

2.3.5 迁移测验材料

包括近迁移与远迁移测验题：前者是与样例题表面特征不同但结构特征相同的相遇问题，后者是与样例题表面特征与结构特征均不同的相遇问题．近迁移与远迁移测验各包括选择题2道，应用题1道，共3道，满分5分．选择题每选对1题记1分．应用题3分，其中计算步骤2分，结果1分．计算步骤与结果均不正确记0分；计算步骤正确结果不正确记2分；计算步骤不完整结果正确记2分；直接给出正确计算结果记1分；计算步骤完整且结果正确记3分．迁移测验材料采用PPT呈现，每张PPT上呈现一道例题，被试要把答案写在答题册相应的题号下．

2.4 实验程序

实验依次包括筛选被试阶段、样例学习阶段、认知负荷测量阶段、工作记忆容量测验阶段与迁移测验阶段．

首先向被试发放“基础知识测试题”，要求被试尽可能准确地计算出每道题，时间为5分钟．待测试结束后，选择那些拥有学习“相遇问题”所需基础知识但同时又不会“相遇问题”的小学生为正式实验的被试．

样例学习阶段：实验分小组进行，每小组6人．在模块样例与模块化样例形式下，向被试依次呈现4道样例，固定推送解释下的指导语是：“同学们，下面我们要学习4道‘相遇问题’的例题以及关于这类题解题过程的解释，请你在6分钟内尽量看懂并记住这类题的解题步骤．”自由选择解释下的指导语是：“同学们，下面我们要学习4道‘相遇问题’的例题，每道题的右上角有关于这类题解题过程的解释，你可以根据自己的需要选择点击‘查看解释’或是‘跳过’按钮．请你在6分钟内尽量看懂并记住这类题的解题步骤．”

认知负荷测量阶段：向被试呈现PAAS量表，心理努力的指导语是：“同学们，现在请你根据刚才的学习状态尽可能准确地评价你学习这类题的心理努力程度，下面1～9个等级代表努力程度递增，1表示非常轻松，5表示中等努力，9表示非常努力．在答题册的9个数字中选择一个合适的数字划‘√’．”任务难度的指导语是：“同学们，你觉得刚才的例题学习有多难，下面1～9个等级代表难度递增，1表示非常容易，5表示中等难度，9表示非常困难．请在答题册的9个数字中选择一个合适的数字划‘√’．”测量时间为2分钟．

工作记忆容量测验阶段：向每小组被试呈现工作记忆容量测验材料，指导语为：“同学们，下面要进行的是一个记忆测验，一会儿PPT会依次呈现3～6个算式，每呈现1个算式时，你要判断这个算式的计算结果是否正确，并在答题册相应题号上划‘√’或‘×’，同时在脑中记住这个算式的第1个数字．接着PPT会呈现第2个算式，你同样需要判断对错和记住算式的第1个数字，依次进行，直到3～6个算式呈现完毕，你要在答题册相应位置上按顺序写下每个算式的第1个数字．”正式工作记忆容量测验开始之前进行2次练习，以确保同学们都掌握了相关操作．测验时间为20分钟．

迁移测验阶段：向被试依次呈现6道测验题，并指导被试在答题册相应位置上作答，测验总时间不得超过15分钟．

实验记录了被试的认知负荷水平、工作记忆容量与迁移测验成绩．

3 实验结果

3.1 样例形式与解释推送策略对小学生数学在线学习中认知负荷的影响

不同样例形式与解释推送策略下被试的认知负荷水平见表1．

为考察样例形式与解释推送策略对小学生数学在线学习中认知负荷的影响，以样例形式与解释推送策略为自变量，以被试的心理努力与任务难度为因变量进行多元方差分析．结果显示，在心理努力上，样例形式的主效应不显著，(3, 124)=0.230，>0.05；固定推送解释下被试的心理努力水平显著高于自由选择解释下的水平，(3, 124)=17.796，<0.001，2=0.126；样例形式与解释推送策略的交互作用不显著，(3, 124)=0.009，>0.05．在任务难度上，样例形式的主效应不显著，(3, 124)=2.269，>0.05；解释推送策略的主效应不显著，(3, 124)=3.510，>0.05；样例形式与解释推送策略的交互作用不显著，(3, 124)=0.390，>0.05．这表明数学在线学习中，模块与模块化样例形式下小学生的心理努力与任务难度水平没有差异；固定推送与自由选择两种解释推送策略下的任务难度水平没有显著差异，固定推送解释下小学生的心理努力水平要高于自由选择解释下的水平．

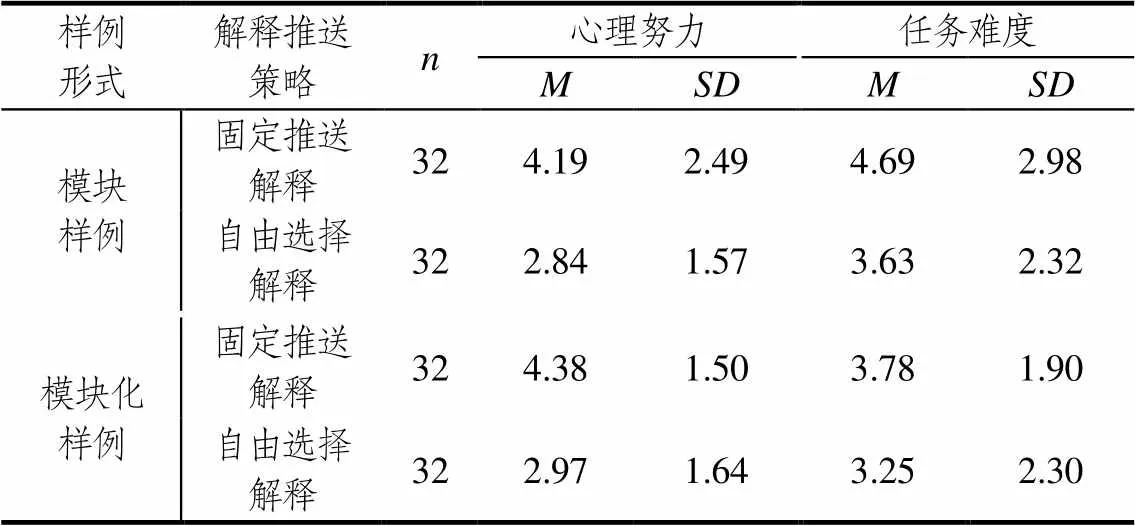
表1 不同样例形式与解释推送策略下被试认知负荷水平

3.2 样例形式与解释推送策略对小学生数学在线学习中工作记忆资源损耗的影响

根据以往研究[18–19]，样例学习后的工作记忆容量代表了被试的工作记忆资源损耗情况，即工作记忆容量越高，代表工作记忆资源损耗越小，反之则越大．不同样例形式与解释推送策略下被试的工作记忆容量见表2．

表2 不同样例形式与解释推送策略下被试工作记忆容量

为考察样例形式与解释推送策略对小学生数学在线学习中工作记忆资源损耗的影响，以样例形式与解释推送策略为自变量，以被试的工作记忆容量为因变量进行单因变量方差分析．结果显示，在工作记忆容量上，样例形式的主效应不显著，(3, 124)=2.895，>0.05；自由选择解释下被试的容量显著高于固定推送解释下被试的容量，(3, 124)= 9.301，=0.003，2=0.07；样例形式与解释推送策略的交互作用不显著，(3, 124)=0.072，>0.05．这表明数学在线学习中，模块与模块化样例形式下小学生的工作记忆资源损耗没有显著差异，固定推送解释下小学生的工作记忆资源损耗显著高于自由选择解释下的损耗．

3.3 样例形式与解释推送策略对小学生数学在线学习中测验成绩的影响

不同样例形式与解释推送策略下被试的近迁移与远迁移测验成绩见表3．

为考察样例形式与解释推送策略对小学生数学在线学习中测验成绩的影响，以样例形式与解释推送策略为自变量，以被试的近迁移和远迁移测验成绩为因变量进行多元方差分析．结果显示，在近迁移测验上，样例形式的主效应显著，(3, 124)=12.472，=0.001，2=0.091，模块化样例形式下被试的成绩显著高于模块样例；解释推送策略的主效应显著，(3, 124)=16.746，<0.001，2=0.119，自由选择解释下被试的成绩显著高于固定推送解释下的成绩；样例形式与解释推送策略的交互作用不显著，(3, 124)=0.380，>0.05．在远迁移测验上，样例形式的主效应不显著，(3, 124)=1.160，>0.05；解释推送策略的主效应不显著，(3, 124)=0.229，>0.05；样例形式与解释推送策略的交互作用不显著，(3, 124)=0.000，>0.05．这表明数学在线学习中，模块化样例形式下小学生的近迁移成绩好于模块样例，自由选择解释下的近迁移成绩显著好于固定推送解释；样例形式与解释推送策略对小学生的远迁移成绩没有显著影响．

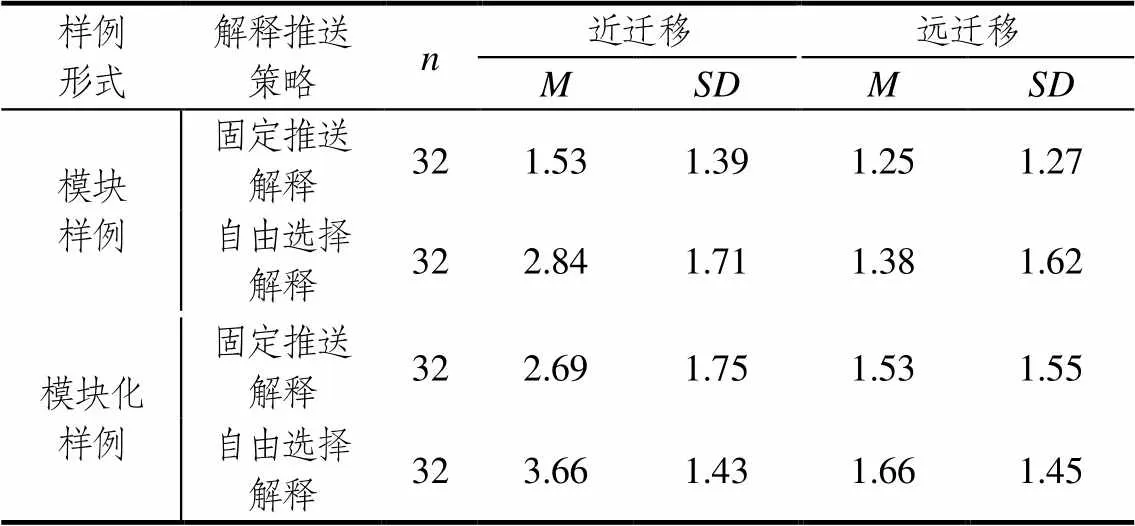
表3 不同样例形式与解释推送策略下被试的测验成绩

4 讨论与建议

4.1 小学生数学在线模块与模块化样例学习中的工作记忆资源损耗效应

以往关于模块与模块化样例学习的研究主要集中于大学生解决“概率问题”，结果发现，模块化样例形式下的学习效果往往好于模块样例形式[8]．为进一步验证模块化样例学习的有效性，研究设计了“相遇问题”的模块与模块化样例，结果发现，模块与模块化样例形式下小学生的认知负荷没有显著差异．这与Gerjets、Scheiter和Catrambone等人的研究结果不一致，他们发现模块化样例形式下大学生的认知负荷水平更低[9]．分析其原因，“概率问题”的模块与模块化样例均包含8个解题步骤，模块样例的各解题步骤均是难度较大的抽象公式、数值代入与计算，而模块化样例的解题步骤大多为结构相似的小事件，因此，模块化样例形式下大学生的认知负荷水平较低．而“相遇问题”的模块与模块化样例的解题步骤均为3步，虽然模块样例的第一步也为解题公式与数值代入，但小学生往往只容易注意表面特征，忽略结构特征[20]，因此，两种样例形式下小学生的主观心理努力与任务难度评分没有显著差异．

以往关于模块与模块化样例学习效果的辅助评价指标是被试的认知负荷，但近年有文献研究提出工作记忆资源损耗直接影响随后的迁移测验成绩[17–18，22]．因此，研究进一步测量了被试样例学习中的工作记忆资源损耗．结果发现，两种样例形式下小学生的工作记忆资源损耗没有显著差异，同时没有表现出工作记忆资源损耗效应．分析其原因，这可能是因为模块与模块化样例包含的解题步骤少，没有超出小学生的工作记忆容量范围[19]，因此，工作记忆资源损耗均较少，而较少的工作记忆资源损耗可能很快就会恢复，不会显著影响随后的近迁移成绩[17–19]．

研究结果还发现，模块化样例形式下小学生的近迁移成绩好于模块样例，两种样例形式下的远迁移成绩没有显著差异．这与研究假设基本一致．与以往研究在近迁移测验成绩上的结果是一致的，但在远迁移测验成绩上的结果是不一致的[4，8–10]．分析原因，“相遇问题”模块样例的第一步包含解题公式与数值代入，是一步高元素交互性的解题步骤[21]，小学生较难发现、理解与记住其中隐含的解题公式，因此，随后的近迁移成绩较差；而模块化样例是把“相遇问题”分解成3个通俗易懂的小事件，并且前两个小事件中包含的均是“时间×速度=路程”公式，小学生很容易理解与记忆这些小事件，因此，随后的近迁移成绩较好．远迁移测验所涉及的题与样例的表面特征和结构特征均不同，难度增大，由于小学生的迁移能力还没有完全发展起来[23]，因此，他们的远迁移成绩均较差．

4.2 不同解释推送策略下小学生数学在线样例学习中的工作记忆资源损耗效应

在线样例学习中，教师往往会根据学生的认知风格和学习需要等因素有针对性地提供教学资源[13，24]．结合以往关于推送策略与解释的相关研究结果[15–16，25]，研究者设计了自由选择解释与固定推送解释．结果发现，自由选择解释与固定推送解释下小学生的主观任务难度评分没有差异，但固定推送解释下的心理努力水平更高．这可能是因为“附加解释”不会增加任务难度，只会导致小学生将注意力过度投入到一些重复性的、不必要的信息上，进而提高了他们的心理努力水平[26]．

研究发现，与自由选择解释相比，固定推送解释下小学生的工作记忆资源损耗更高．分析其原因，固定推送解释下的小学生需要加工许多重复性的信息，心理努力水平更高，而高心理努力会损耗小学生有限的工作记忆资源[18]；而自由选择解释下的小学生可以根据需要选择是否查阅解释，这可能避免了不必要的损耗．因此，工作记忆资源损耗较低．

与自由选择解释相比，固定推送解释下小学生的近迁移成绩较差，两种解释推送策略下的远迁移成绩没有显著差异．这基本验证了以往研究中允许学生自由选择学习内容时的学习效果要好于固定推送学习内容[15–16]，并将其拓展到了模块和模块化样例的解释推送策略中．分析其原因，在自由选择解释下，小学生根据自己的情况选择是否需要查看解释[23]，工作记忆资源损耗也会减少，进而有更多的资源去完成近迁移测验，提高测验成绩．另一方面，自由选择解释可弥补小学生知识上的空缺，帮助他们理解样例中所蕴含的原理与规则[14]，同时也可激发小学生的自主探索活动，提高他们的学习兴趣、学习动机等心理因素[27]，最终提高了近迁移成绩．相反，固定推送解释会向小学生呈现一些重复性信息，而这些信息会消耗他们有限的认知资源，导致工作记忆资源损耗过大，减少了用于完成近迁移测验所必须的工作记忆资源，因此，近迁移成绩较低，表现出工作记忆资源损耗效应．

4.3 教学建议

根据实验结果，小学生数学在线样例学习时应注意以下几点．第一，优先向数学知识初学者呈现模块化样例．模块样例是按整体思路去解题，初学者理解与记忆起来比较困难，模块化样例是按“小事件”去解题，能够促进初学者的理解与记忆，提高学习效果．第二，优先向小学生推荐自由选择解释．与固定推送解释相比，自由选择解释下小学生首先会深入理解样例，然后根据需要选择是否呈现解释，这会避免不必要的解释消耗他们有限的工作记忆资源．第三，关注小学生学习过程中的工作记忆资源损耗．如果学习阶段的工作记忆资源损耗过多，会影响随后的测验成绩，导致测验误差．因此，教师可适当增加在线样例学习与测验之间的时间间隔．

4.4 研究不足与未来研究方向

研究只考察了小学生“相遇问题”在线样例学习中的工作记忆资源损耗效应，其它形式与难度数学内容的样例学习中是否存在工作记忆资源损耗效应还需要进一步验证．同时，研究没有综合考察小学生学习动机与学习态度等因素对工作记忆资源损耗效应的影响．因此，未来关于工作记忆资源损耗效应的研究要扩展研究内容与影响因素，探索小学生工作记忆资源损耗的心理机制．

5 结论

研究设计了固定推送解释与自由选择解释两种推送策略，并考察不同解释推送策略下小学生数学在线模块与模块化样例学习的效果，根据实验结果可得出以下结论：（1）与模块样例相比，模块化样例提高了小学生的近迁移成绩，但没有增加学习过程中的工作记忆资源损耗；（2）与固定推送解释相比，自由选择解释提高了小学生的近迁移成绩，同时降低了学习过程中的工作记忆资源损耗，是一种较为有效的解释推送策略．

[1] SWELLER J, COOPER G A. The use of worked examples as a substitute for problem solving in learning algebra [J]. Cognition and Instruction, 1985, 2 (1): 59–89.

[2] SWELLER J. Cognitive load during problem solving effects on learning [J]. Cognitive Science, 1988, 12 (2): 257–285.

[3] GERJETS P, SCHEITER K, KLEINBECK. Instructional examples in hypertext-based learning and problem solving: Comparing transformational and derivational approaches to example design [M] // NIEGEMANN H M, BRÜNKEN R, LEUTNER D. Instructional design for multimedia learning. Muenster: Waxmann, 2004: 165–179.

[4] CATRAMBONE R. Improving examples to improve transfer to novel problems [J]. Memory and Cognition, 1994, 22 (5): 606–615.

[5] CATRAMBONE R. Generalizing solution procedures learned from examples [J]. Journal of Experimental Psychology: Learning, Memory, and Cognition, 1996, 22 (4): 1 020–1 031.

[6] CATRAMBONE R. The subgoal learning model: Creating better examples so that students can solve novel problems [J]. Journal of Experimental Psychology: General, 1998, 127 (4): 355–376.

[7] MARGULIEUX L E, CATRAMBONE R. Improving problem solving with subgoal labels in expository text and worked examples [J]. Learning and Instruction, 2016, 42 (1): 58–71.

[8] GERJETS P, SCHEITER K, CATRAMBONE R. Designing instructional examples to reduce intrinsic cognitive load: Molar versus modular presentation of solution procedures [J]. Instructional Science, 2004, 32 (1): 33–58.

[9] GERJETS P, SCHEITER K, CATRAMBONE R. Can learning from molar and modular worked examples be enhanced by providing instructional explanations and prompting self-explanations [J]. Learning and Instruction, 2006, 16 (2): 104–121.

[10] GERJETS P, SCHEITER K, CATRAMBONE R. Reducing cognitive load and fostering cognitive skill acquisition：Benefits of category avoiding examples [M]. Mahwah, NJ: Erlbaum, 2003: 450–455.

[11] CALHOUN S P. The effects of using multimedia presentations and modular worked-out examples as instructional methodologies to manage the cognitive processing associated with information literacy instruction at the graduate and undergraduate levels of nursing education [D]. San Francisco: University of San Francisco, 2012: 264–266.

[12] RENKL A. Worked-out examples: Instructional explanations support learning by self-explanations [J]. Learning and Instruction, 2002, 12 (5): 529–556.

[13] RICHEY J E, NOKES-MALACH T J. How much is too much? Learning and motivation effects of adding instructional explanations to worked examples [J]. Learning and Instruction, 2013, 25 (1): 104–124.

[14] WITTWER J, RENKL A. How effective are instructional explanations in example-based learning? A meta-analytic review [J]. Educational Psychology Review, 2010, 22 (4): 393–409.

[15] 林洪新，杨帅峰，杜雪娇．小学生线样例学习的推送策略[J]．电化教育研究，2019，40（11）：121–128．

[16] CHEN X, MITROVIC A T, MATTHEWS M. Learning from worked examples, erroneous examples, and problem solving: Toward adaptive selection of learning activities [J]. IEEE Transactions on Learning Technologies, 2019, 13 (1): 135–149.

[17] SCHMEICHEL B J. Attention control, memory updating, and emotion regulation temporarily reduce the capacity for executive control [J]. Journal of Experimental Psychology: General, 2007, 136 (2): 241–255.

[18] CHEN O, CASTRO-ALONSO J C, PAAS F, et al. Extending cognitive load theory to incorporate working memory resource depletion: Evidence from the spacing effect [J]. Educational Psychology Review, 2018, 30 (2): 483–501.

[19] LEAHY W, SWELLER J. Cognitive load theory, resource depletion and the delayed testing effect [J]. Educational Psychology Review, 2019, 31 (2): 1–22.

[20] CATRAMBONE R, HOLYOAK K J. Learning subgoals and methods for solving probability problems [J]. Memory and Cognition, 1990, 18 (6): 593–603.

[21] HANHAM J, LEAHY W, SWELLER J. Cognitive load theory, element interactivity, and the testing and reverse testing effects [J]. Applied Cognitive Psychology, 2017, 31 (3): 265–280.

[22] 马淑杰，张景斌．高中学生数学原有知识水平和学习认知负荷对数学课堂学习效率的影响研究[J]．数学教育学报，2021，30（1）：26–31．

[23] 林洪新，王云鹏，郑淑杰．小学数学运算规则学习的样例—问题匹配形式[J]．数学教育学报，2021，30（1）：74–78．

[24] 杜雪娇，林洪新．解释的呈现方式对小学生数学样例学习的影响[J]．数学教育学报，2018，27（5）：52–56．

[25] 吕雪，郭力平，李姗姗．反馈对儿童早期数学学习效果的影响元分析[J]．数学教育学报，2020，29（1）：86–92．

[26] SWELLER J. Element interactivity and intrinsic, extraneous, and germane cognitive load [J]. Educational Psychology Review, 2010, 22 (2): 123–138.

[27] FIORELLA L, MAYER R E. Eight ways to promote generative learning [J]. Educational Psychology Review, 2015, 27 (4): 717–741.

The Working Memory Resource Depletion Effect in Mathematical Online Worked Examples Learning

LIN Hong-xin, MA Quan, GUAN Xiao, DU Xue-jiao

(School of Educational Science, Ludong University, Shangdong Yantai 264011, China)

The molar worked examples and the modular worked examples are “one problem and two solutions”. Previous studies have found that the effect of modular worked examples learning is better than that of molar worked examples, but the effects and mechanisms of molar and modular examples with additional explanations are still unclear. The present study investigates the mathematical online learning effect of 128 third-grade primary school students under different learning forms and explanation push strategies. The results show that there is no significant difference in the working memory capacity of students under the molar worked examples and the modular worked examples; the near transfer performance under the mode of modular worked examples learning is higher than that under the mode of molar worked examples learning; and there is no depletion effect of working memory resources. Compared with the free choice explanation strategy, the working memory capacity of the students under the fixed push explanation strategy is lower, their near transfer performance is worse, and the working memory resource depletion effect is observed. This indicates that the modular worked examples can be given priority to the primary school students in the online worked examples learning of mathematics, allowing them to choose the explanation freely and thereby reducing the working memory resource depletion and improving the learning effect.

online worked examples learning; working memory resource depletion effect; primary school students; explanation; push strategy

G40–09

A

1004–9894（2022）06–0024–06

林洪新，马荃，管晓，等．数学在线样例学习中的工作记忆资源损耗效应[J]．数学教育学报，2022，31（6）：24-29．

2022–07–16

山东省教育教学研究青年课题——工作记忆容量对小学生合作样例学习的制约机制及优化策略（2021JXQ004）

林洪新（1980—），女，满族，辽宁鞍山人，副教授，博士，主要从事数学学习与认知研究．杜雪娇为本文通讯作者．

[责任编校：陈汉君、陈隽]