基于EDEM薏苡振动筛清选装置优化设计与试验

周 杨，秦代林，李奇强，聂均杉，罗惠中，张黎骅

（四川农业大学机电学院，四川 雅安 625000）

薏苡作为一种小宗作物，有极高的药用价值[1-2]，但其加工装备缺乏，薏苡物料因组分的复杂性，专用清选装置较少。脱壳后混合物料分离是薏苡加工过程中的重要步骤，主要作用是高效分离出薏苡、破损薏仁、完整薏仁和杂余。分离薏仁损失率与含杂率是评价薏苡清选装置的主要指标[3-4]。现阶段，国内外薏苡专用清选装置的研究鲜有，从薏苡复杂混合物料中分离出薏仁，降低薏苡清选装置的含杂率和损失率成为薏苡加工过程中亟待解决的问题[5-6]。

施丽莉等利用薏苡物料悬浮速度差异，通过在薏苡脱壳腔下方安装单一去杂风机的方式分离杂质[7-8]。王建楠等在薏苡脱壳机中加入两级振动筛对薏苡二次筛选，提升清选效果[9]。随农业机械技术发展，清选装置设计融入新思路。Akbar等利用EDEM软件对振动筛进行建模，研究不同参数对振动筛加工效率和筛网磨损的影响[10]。Dong等采用离散元法在颗粒尺度上考查选煤振动筛的倾斜角度和水平方向的振动幅度对通过量的影响，探讨提高筛分性能的方法[11]。李洪昌等利用EDEM软件对振动筛分过程进行数值模拟，得到透筛率与运动参数（振幅、频率、振动方向角）之间关系[12]。

但国内外学者对薏苡脱出物各组分的不同物料特性与薏苡清选效果的关系进行针对性研究较少，薏苡清选装置专用性不强，清选效果欠佳。本文结合现有问题，设计薏苡专用振动筛清选装置，计算振动筛各基本参数，结合薏苡物料特性建立离散元模型，利用EDEM软件对主要影响因素进行仿真试验，优化振动筛清选装置作业参数，以期获得低损清洁作业效果。

1 结构与工作原理

1.1 整体结构

薏苡脱壳机清选装置分为三级（一级风选、二级复选、三级振动筛），振动筛清选为第三级[13]，主要由筛箱和振动装置两部分构成，如图1所示。其中筛箱主要由侧板、底板、导流板、筛网以及止推杆构成，振动装置主要由连接板、转轴和振幅调节装置构成，通过螺栓与筛箱连接。振幅调节装置主要由薄壁轴承、凸轮、振幅调节板构成，可通过调节振幅调节板的位置改变转轴与凸轮的中心距，实现振幅调节。

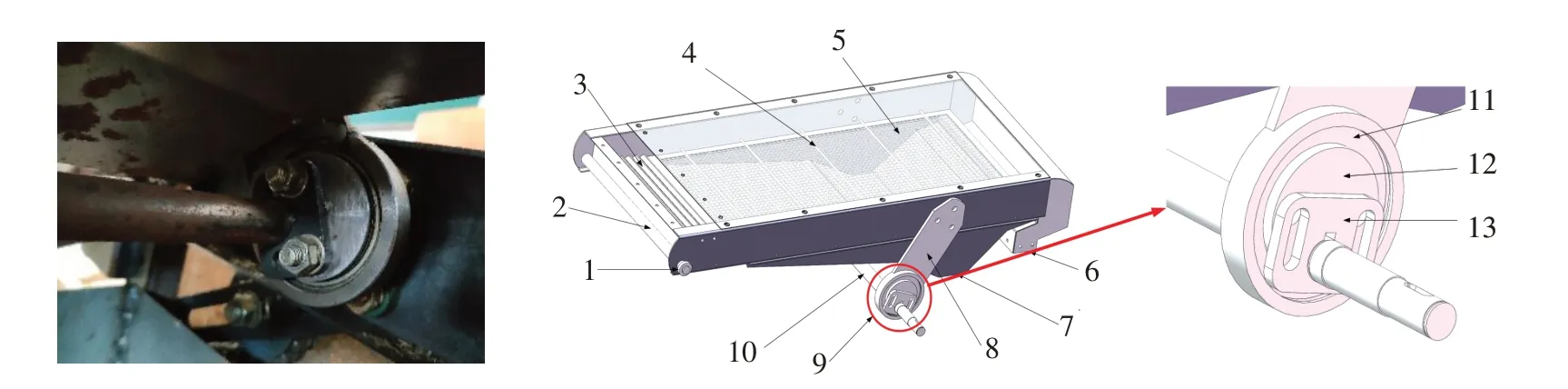
图1 振动筛清选装置Fig.1 Vibrating screen cleaning device

1.2 工作原理

排料装置将沉料仓中物料排入振动筛内，薏苡经筛箱导流板均分至筛网内，在往复振动作用下破碎薏仁等小于筛网尺寸的物料，筛选至筛网下，进入薏仁储料仓。未脱壳薏苡、半脱壳薏苡因几何尺寸大于筛网尺寸无法被筛选，在振动作用下继续运动至筛尾，从复脱出口进入复脱仓，最后在复脱搅龙作用下将物料从复脱仓提升至料仓，完成清选。

1.3 基本参数设计

1.3.1 筛面尺寸

筛面尺寸设计以防堵和高效为目的，以卸料仓落料宽度为设计基础，筛面宽度B与卸料仓落料宽度呈正相关，筛面长度L计算式：

式中，Qs为卸料装置薏苡混合物排出量，本薏苡脱壳机排料速度约为71 kg·h-1；qs为薏苡清选筛单位面积可承担的物料混合物喂入量，取360 kg·（h·m2）-1；筛面宽度B与卸料口宽度一致为0.32 m，计算得振动筛筛面长度L为0.62 m。

1.3.2 筛网孔径

筛网孔径由各项物料占比和尺寸决定。经测量薏仁平均三轴尺寸中最大尺寸为5.875 mm，薏苡及未脱壳物料最小尺寸为5.206 mm。为保证薏仁选择透过性，以薏仁最大尺寸为基准，根据孔径计算式：

式中，D1为薏仁平均三轴尺寸中最大尺寸，D2为筛孔孔径，k为放大系数，取0.8～1.2，计算得孔径范围为5～7 mm。

1.3.3 筛面倾角

建立薏苡颗粒在筛面上运动模型如图2所示。

图2 薏苡颗粒上滑时受力分析Fig.2 Stress analysisof coix particles when sliding up

物料上滑时筛面受力为：

式中，x为筛面位移量，N为筛面支撑力（N）；m为物料的质量（kg）；g为重力加速度（m·s-2）；α为清选筛面倾角(°)；P为颗粒受到振动系统的惯性力（N）；β为振动方向与水平面夹角（°）；

由式（3）可知，在抛起前需克服薏苡滑动摩擦力，为使物料自然后移提高清选性能，需计算筛面倾角，薏苡临界滑动摩擦角与摩擦力关系式为：

式中，Ff为滑动摩擦力，N0为非工作状态下支撑力。由摩擦试验得到临界滑动摩擦角θ为6°。

结合理论计算，本研究利用EDEM软件对振动筛筛网孔型、筛孔孔径、振动频率和振动幅度等影响因素进行仿真试验，优化振动筛最佳作业参数。

2 基于EDEM振动筛关键参数优化

2.1 离散元颗粒模型和几何模型

根据排料装置排出物料实际情况，测量各类物料参数，结果见表1，基于测量参数建立颗粒模型如图3所示，设定所有颗粒模型尺寸在0.8～1.2倍范围内生成。在EDEM软件中设定材料力学特性如表2所示，各材料之间相互作用参数如表3所示。每次仿真时间为5 s，通过质量监视器检测各物料分布情况，评估筛选质量，仿真后处理监测器布置情况如图4所示。

图4 振动筛模型Fig.4 Vibrating screen model

表2 材料力学特性Table 2 Mechanical properties of materials

表3 各材料之间系数参数Table3 Coefficient parametersbetween materials

图3 脱出物简化模型Fig.3 Particle model of the protuberant

表1 薏苡脱出物物料参数Table 1 Material parametersof coix extract

2.2 单因素仿真试验

以物料含杂率、损失率和清选效率为试验指标，筛网孔型、筛网孔径、振动频率和振幅为试验因素[14-15]，参考文中理论计算及文献中振动筛参数[16-17]，利用EDEM进行单因素试验，优选出各因素最佳作业参数[18-19]，仿真试验水平设计如表4所示。

表4 仿真试验水平设计Table 4 Simulation test level design

根据公式（5）～（7）计算筛网含杂率y1、损失率y2和清选效率y3。

式中，mw1为尾筛监测器监测薏苡总质量（g）；mt为尾筛和底筛监测器监测物料总质量（g）；md1为底筛监测器监测薏苡总质量（g）；md为底筛监测器监测所有物料总质量（g）；t为时间（s）。各单因素试验结果如图5所示。

2.2.1 筛网孔型仿真分析

由图5a可知，筛面孔型对清选作业质量影响较大，在相同作业条件下，栅栏筛损失率最低，为13.32%，含杂率较高，为7.46%；方孔筛含杂率最低，为1.93%，损失率相对较高，为17.56%；4种筛面均满足清选速度要求（清选效率≥71.02 kg·h-1），其中方孔筛表现最优，在此作业参数下，清选效率达84.7 kg·h-1。综合所有参数结果，以损失率与含杂率之和最小、清选效率最高为标准，选择筛面孔型为方孔。

2.2.2 振动筛振动幅度仿真分析

由图5b可知，当振动幅度由15 mm降至5 mm，籽粒损失率降低，但含杂率提高，其原因是振动幅度减小，薏苡物料在筛箱内单次运动距离变短，清选时间变长，物料反复运动透筛几率增大导致籽粒含杂率变高。当振动幅度≤5 mm时，薏苡物料在筛箱内单次运动距离过短，无法及时筛选和向后运动，造成物料累积，清选效率急剧降低，达不到工作标准。当振动幅度＞12.5 mm时，物料运动幅度过大，物料在筛面上运动剧烈，薏仁未经筛选便被排至筛尾，造成损失率过高，不满足生产要求。综上，样机振幅拟定于5～10 mm可调，为满足生产要求，需对清选筛作业参数作进一步优化。

2.2.3 筛网孔径仿真分析

由图5c可知，四种筛网孔径清选效率保持在76 kg·h-1均满足清选设计要求。在相同振幅和频率条件下，继续增大筛孔孔径，筛网透筛率增加，导致筛面误选几率增大，底筛含杂率增加；反之筛孔孔径减小，薏仁和破碎薏苡透筛几率变小，导致大量薏仁和碎仁从尾筛随薏苡排出，损失率增加。为避免实际生产效果差异，筛网孔径范围拟定为5～6 mm。

2.2.4 振动筛振动频率仿真分析

综合图5d可知，清选损失率和清选效率均随振动频率提高而增加，振动频率≤10 Hz时底筛含杂率较低，小于5%。振动频率＜7.5 Hz，清选效率明显降低，大量物料累积在筛网上，导致清选装置出现堵塞，无法满足作业要求。当振动频率≥10 Hz，物料在筛箱内跳动次数增加，大量碎仁被抛向尾筛，损失率显著增加。因此，为在实际样机中优化出最佳作业参数，振动筛样机振动频率拟定于5～10 Hz可调。

图5 各试验因素对作业质量的影响Fig.5 Influence of varioustest factors on operation quality

3 响应面仿真试验

3.1 二次正交旋转组合试验设计

依据单因素试验结果，参照种子清选机试验方法国家标准GB/T5983-2013[20]，以籽粒含杂率、损失率为薏苡清选装置试验指标。借助Design-Expert软件，按照中心组合响应曲面设计（Central composite design，CCD）试验方案[21-22]，分析回归模型含杂率Y1、损失率Y2，试验因素编码如表5所示。

表5 试验因素和水平编码Table 5 Coding of test factors and levels

3.2 振动筛试验结果与分析

试验设计与结果、方差分析情况见表6和7。可得出粒含杂率Y1与籽粒损失率Y2回归方程，并作显著性检验。

表6 响应面试验设计与结果Table 6 Response surfacetest design and results

表7 含杂率和损失率回归方程方差分析Table 7 Analysis of variance of regression equation of impurity content and loss rate

3.2.1 含杂率分析

由含杂率方差分析可知，模型显著性检验P值＜0.001、失拟项＞0.05、模型决定系数分别为R2=0.9966、模型矫正系数R2adj=0.9921，说明所得回归数学模型与实际结果拟合精度高。清选装置筛孔孔径（A）、振动幅度（B）、振动频率（C）、A2和C2对含杂率有极显著影响，存在非线性关系，B2对含杂率有显著影响，而交互性AC、BC和AB对含杂率无明显交互影响，各因素影响振动筛清选装置含杂率主次为：A、A2、B、B2、C、C2、BC、AC、AB。由多元回归分析得到含杂率与试验因素回归方程为：

各试验因素作用对含杂率响应曲面见图6，（A）筛孔孔径、（B）振动幅度和（C）振动频率3个一次项对薏苡含杂率均有显著影响，由等高线密度和响应曲面形状可知（A）筛孔孔径交互曲面变化最快，（B）振动幅度和（C）振动频率变化相对较缓，因此（A）筛孔孔径影响最大；（A）筛孔孔径、（B）振动幅度和（C）振动频率之间两两交互作用对振动筛清选装置含杂率影响并不明显，与含杂率方差分析结果一致。

图6 含杂率响应曲面Fig.6 Impurity rate response surface

3.2.2 损失率分析

由损失率方差分析可知，模型显著性检验P值＜0.001、失拟项＞0.05、模型决定系数R2=0.9915、模型矫正系数R2adj=0.9807说明回归模型与实际结果拟合精度高，此模型可对含杂率进行分析和预测。由P值可知，清选装置筛孔直径（A）、振动幅度（B）、振动频率（C）、A2、B2和C2对损失率均有极显著影响，存在非线性关系，交互性AB、AC对含杂率有显著影响，BC对含杂率无明显交互影响。根据模型各因素回归系数大小，可判断各影响因素影响振动筛清选装置损失率主次为：A、A2、B2、C2、B、C、AB、AC、BC。由多元回归分析得到损失率与试验因素回归方程为：

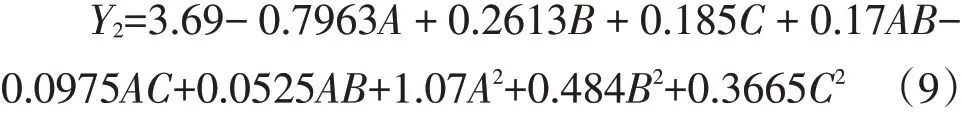
由图7可知，（A）筛孔孔径、（B）振动幅度和（C）振动频率3个一次项对薏苡损失率均有显著影响，由等高线密度和响应曲面形状可知（A）筛孔孔径交互曲面变化最快，（B）振动幅度和（C）振动频率变化相对较缓，因此（A）筛孔孔径影响最大；（AB）和（AC）交互作用对振动筛清选损失率有一定显著影响；（BC）交互作用对振动筛清选装置损失率影响并不明显，与损失率方差分析结果一致。

图7 损失率响应曲面Fig.7 Loss rate response surface

3.3 最优工作参数确定

以含杂率和损失率最小，优先保证含杂率为优化目标，对振动筛清选装置进行参数优化，并建立Y1、Y2双目标函数数学模型，将含杂率重要性设置为5个“+”，损失率次之设置为3个“+”，3个因素目标设置在优化范围内。

优化结果为：（A）筛孔孔径为5.46 3 mm、（B）振动幅度为7.626 mm、（C）振动频率为7.637 Hz时，薏苡含杂率为1.05 4%、损失率为3.783%。将此最优参数圆整后进行样机验证试验。

3.4 样机验证试验

为确保每组清选试验同一性，试验选用康莱特薏苡为研究对象，将3 kg薏苡样品连续脱壳后经二级复选装置脱出的薏苡物料混合物为试验材料，各成分占比如表8所示。

表8 薏苡脱出物各物料成分百分比Table 8 Percentage of each material of coix extract

参数圆整后进行样机验证，试验结果为：含杂率为1.297%，损失率为3.562%，与优化结果一致，表明优化结果具有较高可信度，本研究模型可靠。

4 结论

a.为降低薏苡清选过程中损失率与含杂率，通过分析工作原理，结合薏苡物料特性，建立颗粒运动模型，并计算参数，设计一种薏苡专用清选装置，可为薏苡清选装置结构设计与优化提供参考。

b.采用EDEM仿真方法，建立离散元仿真模型。基于单因素试验结果，开展三因素三水平二次正交旋转组合试验，得到筛孔孔径、振动幅度、振动频率与损失率、含杂率之间数学回归模型。以含杂率和损失率最小，优先保证含杂率为优化目标，得到最优设计参数组合为：筛孔孔径为5.463 mm、振动幅度为7.626 mm、振动频率为7.637 Hz。

c.根据优化参数（圆整）进行样机验证试验，含杂率和损失率分别为1.297%、3.562%，均符合国家标准。验证试验结果与优化模型预测值相吻合，优化参数可靠。表明本薏苡清选装置可对薏苡物料进行有效清选，满足薏苡清选作业要求。