基于Partial-EIV的数据探测法研究

王铮尧， 梁 菲

(中煤航测遥感集团有限公司技术发展研究院，陕西西安 710199)

0 引言

研究和处理粗差对平差结果的影响方法主要分为两类，第一类是将粗差放在函数模型中进行处理的均值漂移，另一类则是将粗差放在随机模型中进行处理的抗差估计[1]。本文仅考虑均值漂移模式下的主要方法，包括：Data-Snooping，QUAD，LEGE，部分最小二乘法等[2-5]；宋力杰等通过计算分析，得出Data-Snooping与LEGE法在原理上基本等价[6]。上面提到的一些粗差处理方法都是在最小二乘基础上进行拓展构建的，但是对于观测值以及法方程中系数同时存在误差的EIV模型进行粗差探测的解决方法相关文献研究较少。Schaffrin等在观测值和法方程中系数等权以及法方程中系数误差为随机误差的条件下推导了EIV 模型的可靠性公式[7]；徐培亮通过将法方程中系数中的随机元素和固定元素进行推导分离，构建了Partial-EIV函数模型[8]；曾文宪在Partial-EIV函数模型的基础上，分析构建出EIV模型的可靠性公式，进一步获得了该模型中观测值和法方程中系数的最小可发现粗差[9]；Amiri-Simkooei和Shahram-Jazaeri利用EIV模型整理变化为最小二乘形式，构建了EIV-Data-Snooping[10]。

本文的目的旨在更好的解决EIV模型中观测值与法方程系数都存在粗差的问题，文献[10]中的方法虽然可以发现并剔除数据中的粗差，但是不能区分出该粗差是存在于观测值还是法方程系数矩阵中，所以本文所提出在Partial-EIV模型的基础上构建的数据探测法，该方法不仅可以发现并剔除数据中的粗差，而且可以区分出粗差所存在的具体位置。

1 Partial-EIV模型

EIV函数模型是处理观测值与法方程中系数都存在误差最为经典的模型，具体公式：

y=(A-EA)x+ey

(1)

式中：y是观测值向量；ey是y的误差向量；A是系数矩阵；EA与x是系数误差阵以及待求参数。

本方法是基于Partial-EIV模型进行构建的，所以需要引入Partial-EIV模型，该模型基础方程是在公式(1)的基础上进行分离拓展构建的，具体见下式[8]：

(2)

方程中的观测值与法方程系数所服从的误差模型：

(3)

由于公式(2)为非线性公式，所以将该模型在已知值(α0,β0)处，进行泰勒级数展开，并进行化简整理得出[9]：

(4)

(5)

将上述公式进行进一步化简，推理导出：

(6)

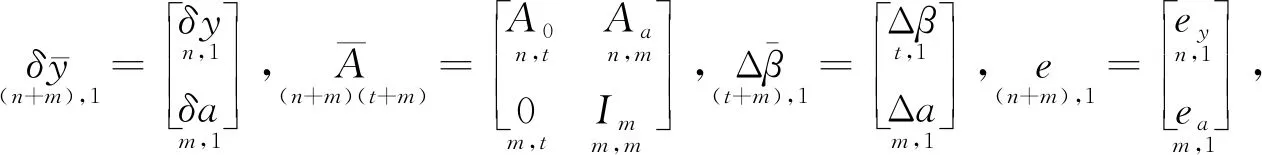
该模型以公式(7)为条件进行优化：

(7)

(8)

(9)

(10)

2 基于Partial-EIV模型的数据探测法

如果函数模型中相关的变量存在粗差，该粗差造成的影响会在残差中表现出来，所以通过验前和验后的单位权方差是否一致可以发现模型中的粗差。

所用的原假设与备选假设[11]：

(11)

利用公式(9)、(10)以及(11)构建该方法的统计检验量：

(12)

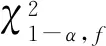
在标准差已知的情况下，检验量计算公式[13-15]：

(13)

在标准差未知的情况下，检验量计算公式为：

(14)

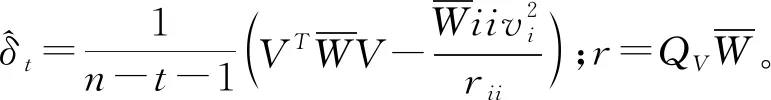
满足条件|wj,N|≥|wi,N|，∀i=1,K,m,and |wj,N|>Nα/2(0,1)(标准差已知的情况)或者|tj|≥|ti|,∀i=1,K,m,and |tj|>tn-t-1(标准差未知的情况)，那么观测值含有粗差。以上便是本文所构建方法的推导过程。

3 算例分析

3.1 直线拟合算例

计算时，拟合方程为y=kx+b，存在粗差以及剔除粗差后的平差结果见表2。

表1 两种方法发现粗差结果比较

表2 含有粗差和剔除粗差的计算结果对比

3.2 平面坐标转换算例

算例2中的数据为进行坐标转换的数据，表3为坐标转换数据的详细信息，为了方便测试算法的计算效果，在起始坐标系第四点横坐标us处加入0.1的粗差，且进行坐标转换的两组数据的标准差都是0.01，结果见表4。

进行坐标转换时，所采用的模型为[14，19-21]：

[a1b1c1a2b2c2]

(15)

存在粗差以及剔除粗差后的平差结果见表5。

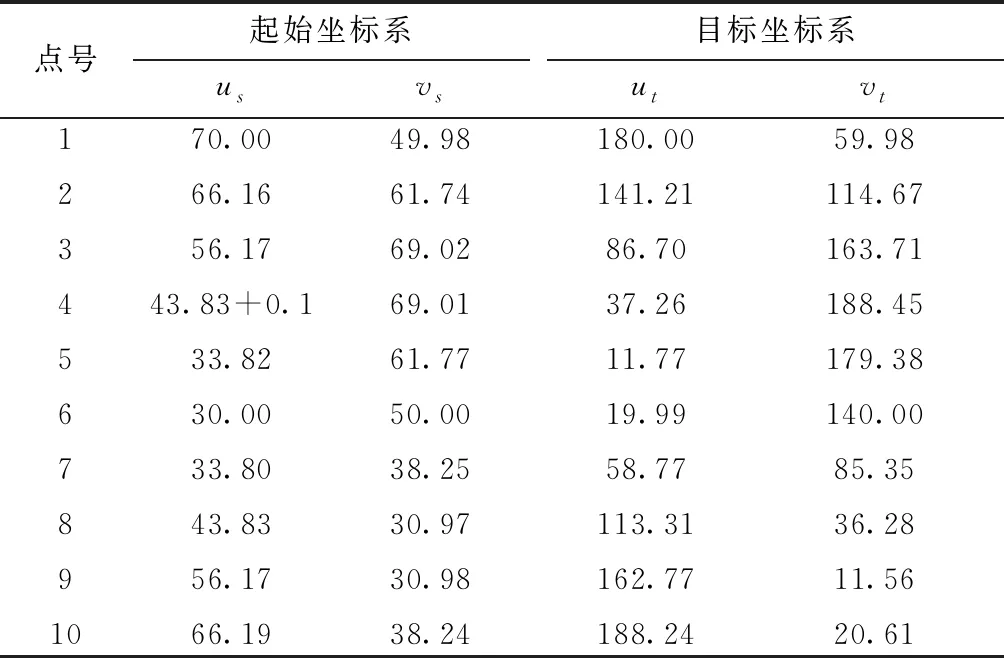
表3 坐标转换的原始数据

表4 两种方法发现粗差结果比较

表5 含有粗差和剔除粗差的计算结果对比

4 结论

假设观测数据之间是独立对等的，并且数据中存在粗差，对计算示例的结果进行分析对比后，得出以下结论：

1)本文所构建的计算方法可以较好的确定观测值中粗差的位置以及反映法方程系数中所存的粗差，并将其剔除，弥补了文献[10]的方法中不能反映法方程系数粗差问题的缺陷。

2)当剔除粗差以后，平差的计算结果得到明显的改善，计算所需的迭代次数也明显减少，进一步也说明了本文方法的有效性与可实用性。

当观测数据存在多个粗差时，可采用循环迭代的计算方式进行剔除，直到没有统计检验量超限，对于粗差较小的情况以及观测数据之间存在相互影响情况下的粗差剔除，下一步将继续研究。