应用于腐蚀监测的金属探针阻值测量方法
2022-12-26王选择张瑜灿王浩伟
王选择,郑 烨,张瑜灿,王浩伟
(1.湖北工业大学机械工程学院,湖北武汉 430068;2.中国特种飞行器研究所,结构腐蚀防护与控制航天科技重点实验室,湖北荆门 448035)
0 引言
在石油、化工、动力、食品等工业中,广泛使用的设备在恶劣的环境下,其主要部件的金属会发生腐蚀现象,金属溶解释放出电子,其环境介质如氧气接受电子,这种腐蚀反应会在金属的各个位置同时发生[1],最终使得其阻值发生改变。由于金属的阻值本身很小,腐蚀条件下产生的阻值变化十分微小,因此获取腐蚀过程中金属阻值反应腐蚀状态对设备的安全运作、及时维修起到重要的作用。采用电阻探针方法[2],通过对其阻值的测量来反应设备某一特定位置腐蚀速率的大小,及时反馈该位置腐蚀变化的趋势,比其他方法测量简便迅速,信号反应快且不受腐蚀介质的影响。
对于反应金属腐蚀变化状况分为直接法与间接法。直接法是通过失重法[3-4]来展现腐蚀的效果。间接法是通过测量其阻值的变化来换算成金属腐蚀减薄量[5]。传统的电阻方法有伏安法[6]、惠斯顿平衡电桥[7]和非平衡电桥法[8]。失重法无法实现实时、自动化的测量要求。传统的电阻测量法难以满足高分辨力测量要求。
基于伏安法的四端测量法[9],通过供给恒定直流电流的方式,加载待测电阻上,截取电阻两端电压进行放大后,运用欧姆定律直接计算出待测电阻阻值,由于该测量系统使用恒定直流电流驱动,无法克服低频噪声的干扰且放大倍数有限。改进的测量方法加入参考电阻与待测电阻串联后形成类电桥方式,当待测电阻与参考电阻很接近时,待测电阻与参考电阻两端电压也很接近,此时差分信号可以进行较大倍数的放大,但仍难以消除低频噪声的影响,并且要求参考电阻接近待测电阻的局限性。采用ZFCT参考比臂的方式[10],可以克服这种局限性,不要求两者接近相等。主要是通过电流互感器[11]与瓦格纳电路相结合,调整一次、二次绕组的匝数,从而调节瓦格纳电路使其达到近似平衡,实现待测电阻与参考电阻之间的电压差值近似为0,保证后续差分信号的高倍放大,进而实现电阻的精确测量。由于该方法受调整档位的限制,很难达到待测电阻连续变化条件下的平衡,且电路调节步骤较复杂,实时性差。
为此,本文提出一种双激励交流源驱动与自平衡补偿相结合的高精度阻值测量方法。该方法采用STM32F407单片机DAC转换模块[12],与双三极管组成的复合管生成稳定高效的可控交流源信号,并通过差分处理与自平衡补偿调节方法,一方面克服高低频噪声的影响,另一方面完成差动信号高放大倍数,最终实现高分辨的腐蚀速率实时监测。
1 腐蚀探针电阻计算原理
腐蚀检测系统采用电阻探针的原理是依据测量腐蚀过程中腐蚀金属电阻变化从而求出其腐蚀量和腐蚀速率。在任何时刻,金属导体的电阻与其长度和电阻率成正比,与其横截面积成反比,图1为圆柱形的金属丝。
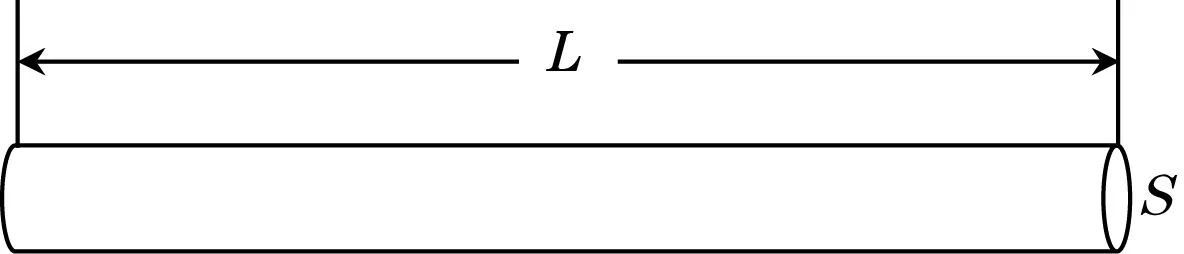
图1 简化金属丝模型

(1)
式中:L为长度;ρ为电阻率;S为横截面积;d为金属丝的直径。
由式(1)可知,长度一定的金属材料在腐蚀减薄后其截面积会随之减小,从而电阻增大。因此只需知金属在腐蚀环境中其电阻的变化量,即可计算出金属的减薄量,其计算公式为:
(2)
由此可以推导出t时刻金属的腐蚀深度Ht为:
(3)
式中:R0、Rt为金属丝初始阻值和t时刻金属丝的电阻值;d0为金属丝原始直径;Ht为t时刻金属的腐蚀深度。
对于2个时刻t1、t2之间金属腐蚀深度的变化,可用公式(4)计算此期间内金属的腐蚀速率:
(4)
式中:v为金属腐蚀速率;Ht1、Ht2为t1和t2时刻对应金属探针的腐蚀深度。
因此,通过检测金属丝的阻值变化,应用式(3)计算在直径方向上的腐蚀深度,则可间接反应出金属在腐蚀环境中的变化情况。由于金属丝阻值本身很小,在腐蚀过程中产生的变化十分微小,故需设计微小电阻的测量系统,且该系统还需具备对金属阻值的高分辨测量能力。
2 测量方案的确定
2.1 双激励测量原理
针对ZFCT参考比臂测量法的不足,本文设计如图2所示的同源双激励法进行电阻测量。使用STM32F407单片机DAC1、DAC2模块产生的电压经过V/R转换电路,生成两路稳定可控的交流源Ii1、Ii2,交流源电流在参考电阻和待测电阻上形成可分辨的电位Uf、Um,将两电压信号分别引入差分放大电路,然后将差分放大信号送入STM32单片机12位A/D转换器进行数模转换,经过单片机内部对相应数据的处理,计算金属对应电阻值。则有
Uf=Ii2·Rref
(5)
Um=Ii1·Rm
(6)
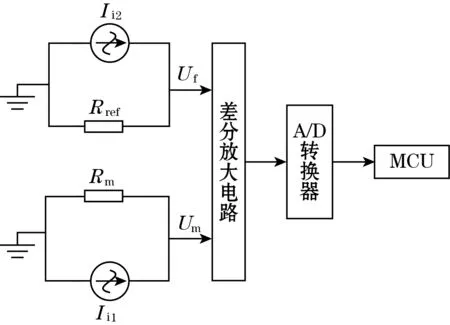
图2 双激励测量电路整体设计框图
假设差分放大倍数为k,输出为Vo,则有:
Vo=k(Uf-Um)=k(Ii2·Rref-Ii1·Rm)
(7)
那么
(8)
根据式(8)可知,若Ii1,Ii2已知,k为常数,则Rm测量的误差来源于Vo,假设由Vo引入的随机误差为δ,则对于Rm测量时的误差为:
(9)
显然,增大差分放大倍数k,一方面可以减小测量时的误差,另一方面倍数大测量时的分辨力高。但在实际测量过程中放大倍数不可能无限大,因此在放大倍数k一定的情况下,为了最大程度上消除测量时的误差,采用交流调制激励的方式,可以尽量抑制噪声与工频干扰的影响,但在放大过程中,由于k过大,输出较易饱和,为了消除饱和带来测量分辨力不足的影响,采用软件的方式调整DAC1或DAC2输出电压幅值大小,本设计是通过对DAC1也就是Ii1进行调整,最终使得电路达到平衡状态,实现差动信号的高放大倍数。
2.2 交流源电路设计
图2所示的交流源电路的等效电路如图3所示。该电路主要是由可控电压源、待测电阻或参考电阻和集成运算放大器与双NPN型三极管共同组成的V/R转换电路组成,其输出电流幅值可以通过程序进行控制。该电流源电路的核心设计原理:由单片机DAC1或DAC2模块输出的DDS信号[13]作为电路的外激电压源,通过三极管正常工作下的特性与运放负载电压反馈,在精密电阻R0上产生压降,则与该精密电阻相串联的支路上就可以得到稳定、高精度的可控交流源。
图3中,VDAC为单片机DAC转换模块输出的可调电压源VDAC1或VDAC2;Q是由Q1、Q2组成的复合管,为了驱动较大的电流,一般采用两级的方式,能够弥补单运放驱动大电流能力不足的缺陷;Rm、Rref为待测电路与参考电阻,其中IC等效为图2所示的Ii1或Ii2。
根据NPN三极管、运算放大器虚短、虚断的特性,由图3可得:
IE=IB+IC
(10)
(11)
(12)

则根据式(11)与式(12)可得Ii1=VDAC1/R0或Ii2=VDAC2/R0,从而可以得到对应的Um、Uf:
Um=-Ii1·Rm+VCC
(13)
Uf=-Ii2·Rref+VCC
(14)
2.3 差分放大输出信号的分析
差分放大电路如图4所示。将电压信号Um、Uf引入至差分电路,通过运算放大器与各电阻之间的数量关系,最终将包含金属阻值的电压信号进行高倍数的放大,增强测试信号的信噪比。电路中引入的VCC是保证输出信号的直流分量为1.65 V。
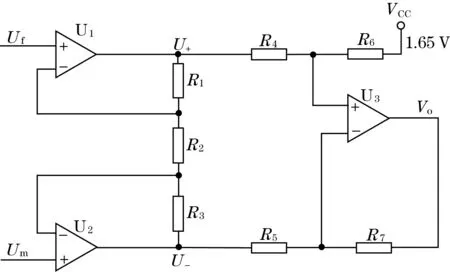
图4 差分放大电路
由运算放大器虚短、虚断性质可建立公式:
(15)
(16)
(17)
取R1=R3=64R2;R4=R5=R6=R7,则由式(15)~式(17)可以推导出:
Vo=129×(Ii1·Rm-Ii2·Rref)
(18)
那么
(19)
如果Ii1=Ii2,在腐蚀刚开始阶段,Rm值不改变,加载的2个交流源是依靠同一参考源的DDS信号转换而来,其携带的电源与各频段的噪声理论上是一致的,因此通过式(18)可以相互抵消。但腐蚀过程中由于Rm不断变化,放大倍数k=129过大,会导致输出Vo饱和。为了满足高分辨力的要求,通过调整DAC1,改变Ii1电流幅值大小,通过式(18)能够保证输出信号放大不饱和。
理想情况下,输出Vo应满足如下规律:当Rm
从图5可知输出信号的解算需同时涉及到信号的幅值移与相位移。以激励VDAC1为参考,输出与VDAC1相差为0时设输出为正,同理相差为180°时输出为负,电路平衡点为相差90°其输出设为0,则差分输出信号表示为
Vo=Ao·cosφ
(20)
式中:Ao为输出信号的幅值;φ为输出信号Vo与激励VDAC1之间的相差。
2.4 自动平衡补偿软件调节流程
自动平衡补偿流程如图6所示,程序开始运行并初始化各功能后,使用STM32单片机A/D转换模块对激励VDAC1以及输出Vo进行采集。判断Vo与VDAC1之间的相位关系,通过程序对Ii1进行实时调整,直到输出信号与激励DAC1之间的相差接近90°,实现电路自平衡补偿调节。
3 测试信号的处理
通过单片机DAC模块产生的正弦交流信号,作为输入信号VDAC1、VDAC2,其幅值分别为A1与A2,两输入信号的频率均设定为1 kHz。对输入信号VDAC1与输出信号Vo通过同步模数转换器(ADC)进行采样,并用数字正弦拟合处理数据,得到其幅值比Ao/A1与相位差φo-φ1。
假设输入信号的表达式为:
(21)
则输出信号的表达式为
Vo=Aocos(φo-φ1)
(22)

(a)同相

(c)相差90°图5 差分输出与激励DAC1相位关系图
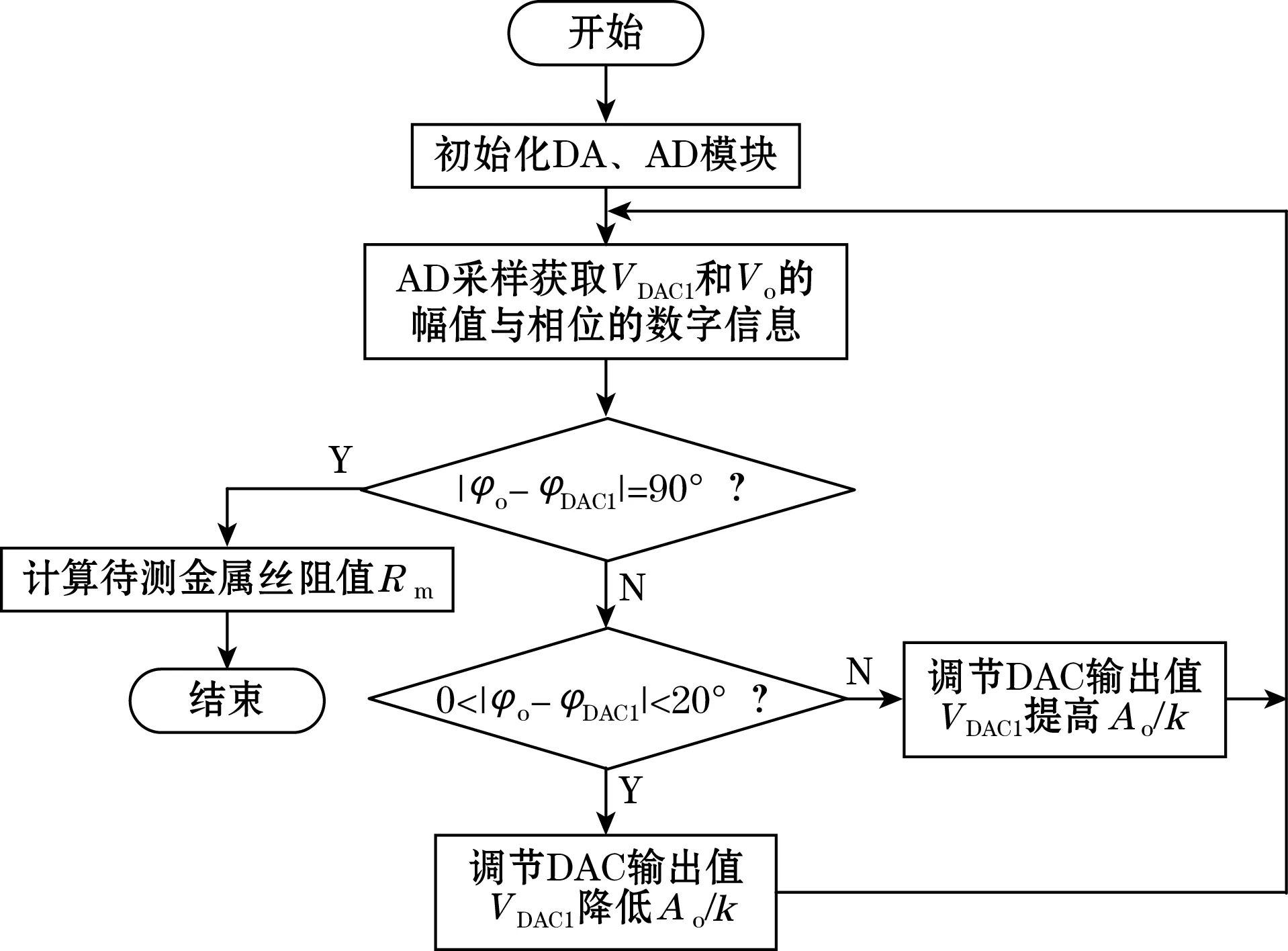
图6 自动平衡补偿流程图
式中:ω为角频率;φ1、φ2分别为DAC1和DAC2输入信号的初始相位,设定φ1=φ2;φo为输出信号初始相位。
由于DAC2输出值不变即拟合出的A2为常数,故可令k1=A2·Rref,k2=R0/129,则待测电阻Rm计算公式可重新表示为
(23)
3.1 信号的采集
本设计使用的STM32F407单片机拥有3个分辨率为12位的逐次逼近型的ADC转换模块,采样频率能够达到1 MHz以上。为对上述2个信号进行同步采样,故该系统采用双重规则同步采样模式,使用TIM更新事件触发,以及DMA数据传送方式,将ADC转换的数据依次传送到STM32内部SRAM。采样方案如表1所示。为了保证系统良好的实时性,程序上采用边采集边处理的方式,且数据处理的时间为2 ms,。ADC采样频率设定为100 kHz,采样周期为10 μs,则每个周期采样100点,每个通道采集8个周期,2个通道采集数据量为1 600点,采样时长为8 ms。

表1 双重AD采集方案
3.2 信号幅值与相位求解
由式(23)可知,待测电阻阻值的计算与输入和输出之间的幅值比、相位差相关,且为了实现自平衡的调整,需要得到信号的幅值与相位,采用如下的方法对采集的信号进行正弦拟合,得到其幅值与相位信息。
设经过AD采样后的正弦函数的数学模型为:
Xi=Acos(Δi+φ0)+C+εi
(24)
式中:Xi为离散采样数据;i为采样序列,i=0,1,2,3,…,n-1,n为采样总长度;A为幅值;Δ=2πfDAC1/fs,fDAC1为输入信号的频率,fs为采样频率;φ0为采样信号的初始相位;εi为采样误差。
令a=A·cosφ0,b=-A·sinφ0,则式(24)可表示为
Xi=acosΔi+bsinΔi+C+εi
(25)
根据最小二乘线性拟合[14],a与b可表示为:
(26)
于是
(27)
将所求的幅值A与相位φ0带入式(23),即可计算出待测电阻的阻值。
为了测试系统长时间测量的稳定性,对激励与输出信号输出的电压值进行同步ADC采集,通过程序计算出两者的幅值比与相位差,并保存这段时间的数据,测试时长为10 min。绘制出幅值比与相位差随时间的变化曲线,如图7所示。

图7 实测幅值比与相位差曲线图
图7中,在10 min内测量输出与输入之间的幅值比与相位差的均值分别为1.172 3和1.004 6°,实际测量的幅值比波动量小于0.003 8,相位差波动量小于0.08°。通过曲线可以看出长时间测量波形比较稳定,无太多的跳跃变化,测量系统具有较强的稳定性。
4 实验结果
实验采用的金属丝其相关参数为:长度L= 0.1 m,直径d=0.5 mm,电阻率ρ=3.49×10-7Ω·m(室温25 ℃)。通过式(1)计算出金属丝初始阻值为178 mΩ。以该金属探针离线腐蚀在盐雾箱内的腐蚀测量数据为例,采集数据的时间间隔为24 h,以此反馈该时刻金属探针阻值的变化。在7 d内金属探针离线测量的电阻值随时间变化曲线如图8(a)中Rt所示,从而根据式(3)推算出对应时刻的腐蚀减薄量,其随时间变化曲线如图8(a)中Ht所示。从图(a)中可以看出随着时间的延长腐蚀减薄量的增加近视于线性的关系。由式(4)可知,金属的腐蚀速度等于每个时间间隔内腐蚀深度的直线斜率,从而采用一元线性回归方法对减薄量曲线进行拟合,实验结果如图8(b)所示。拟合方程为H(t)=0.586 7t-0.125 6,则金属丝的平均腐蚀速度为0.586 7 μm/d。

(a)腐蚀深度曲线

(b)腐蚀深度线性拟合曲线图8 实验结果图
在均匀腐蚀条件下,以h单位,则在金属丝直径方向上的分辨率为Δd=0.024 4 μm,通过质量计算公式m=ρ′V,其质量分辨率可由式(28)计算得到:
(28)
式中:Δm为金属质量分辨率;ρ′为金属密度。
为了准确计算其分辨力,首先需利用电子天平称重(精度为0.000 1 g),金属丝的质量为155 mg,从而计算出其密度为7.89 g/cm3,通过公式(28)可得金属丝的质量分辨率为30.24 μg。金属探针质量的变化最终体现在阻值上的变化,依据金属阻值的计算公式得出该段时间内阻值变化量,从而推算出其阻值的分辨力为17.35 μΩ。
5 结论
结合STM32单片机技术,通过其DAC转换模块与三极管相结合输出稳定可靠的可控交流源,并通过自平衡补偿法消除测量时携带的干扰信号,较大提升了阻值测量的分辨力。通过实验得到金属丝腐蚀的速率为0.024 4 μm/h,在均匀腐蚀条件下金属丝的阻值分辨力为17.35 μΩ,其质量分辨率为30.24 μg。该测试系统电路简单,稳定性高、具有较高的阻值分辨力,在腐蚀电阻探针方面具有很好的参考价值。
