单光场时栅位移传感器散射角误差分析及优化

付 敏，乔俊红，朱 革，冷从阳，魏晓波

(1.重庆理工大学机械工程学院，重庆 400054；2.重庆理工大学机械检测技术与装备教育部工程研究中心，时栅传感及先进检测技术重庆市重点实验室，重庆 400054)

0 引言

精密位移测量是精密加工制造的关键因素[1]。近些年，随着航空航天、超精密加工[2]等领域快速发展，对加工精度要求越来越高，从而对位移测量的精度和分辨力也提出了更高的要求。在众多精密位移测量方法中，光学位移测量应用广泛。目前，精密测量光学领域从光信号产生原理上主要分为利用光波干涉现象的激光干涉仪和利用光强等空间透射与遮挡的光栅传感器。激光干涉仪是在传播过程获取两路不同相位的干涉光信号实现以光波波长为基准的高精度位移测量[3]，但利用直接暴露在测试环境的光线作为测量尺，其测量精度和稳定性受空气扰动、噪声及温湿度等外界干扰大，常应用于环境好的实验室或作为精度标定使用[4]。光栅是对标尺光栅和指示光栅相互运动形成的摩尔条纹进行计数来实现位移测量[5]，其测量原理是对光强进行空间细分，测量精度由栅线精度和光强精度两方面决定。一方面，为提高栅线细分精度，普遍的方法是尽可能减少栅距大小，但受光学衍射极限和制造工艺限制[6-8]。目前制造水平局限在亚μm量级，且制造难度和成本非常高，难以从刻线密度方面来进一步提高，但可以从细分倍数来提高精度。文献[9]利用智能锁相进行细分，采用倍频算法达到细分效果，但容易受到原始信号直流偏量及高次谐波干扰产生细分误差。另一方面，随着栅距减小对光源准直性的要求随之增加，而为减少准直对测量精度的影响，普遍采用的方法是减少光照接收区域，以减少光强分布造成空间细分光强的影响[10]。文献[11]利用重复光刻的方式周期性叠加不同位置的光强，使其能量分布一致来减小俯仰误差对精度的影响，但降低了光强峰值，也对显示阈值的精度有了更高的要求。

因此可知，为提高光栅测量精度会尽可能增加刻画密度减少栅距，而栅距减小对光源要求则越来越高。因此，文献[12]提出一种放大栅距进行光场调制的位移测量方法,用正弦透光面阵列，对光场分布进行空间调制从而实现高精度位移测量，但随着栅距增大，对光源照射区域范围也随之增加，且对光源出光质量要求进一步提高。因此，本文提出一种对单光场时栅位移传感器光源散射角进行优化的方法。根据单光场测量原理和前期实验分析，建立单光场时栅位移传感器散射角理论误差模型，明确了光源散射会对接收到的透光面的栅距和幅值有所影响，导致行波信号产生误差。针对这一问题设计适用于光源的准直透镜，减小光源散射角对四路信号的影响，达到减小测量误差的目的。

1 单光场时栅位移传感器测量原理

单光场时栅位移传感器测量原理如图1所示，光源、定尺及接收装置固定在光学实验平台上，动尺安装于直线导轨。空间调制是动定尺相互运动实现，定尺由4组余弦透光面阵列组成，4组透光面错开1/2栅距宽度，动尺由遮、透光相互交替的矩形透光面组成。当动尺匀速运动产生空间变化，已调制的光信号通过空间调制得到四路驻波信号，0°的电信号与180°电信号合成一路电信号，90°的电信号和270°的电信号合成另一路，然后将其一路电信号进行90°移相，对两路信号进行合成得到行波信号。

图1 单光场时栅位移传感器测量原理图

详细的光场时栅位移传感器原理见文献[13]，最后的行波信号可以表示为

(1)

式中：A为定尺余弦透光面幅值；W为动尺栅距；K=4AW/π；x为移动的距离。

将该信号转为方波与光源激励方波信号进行比相得到相位差，从而实现位移测量。

2 散射角误差分析

根据单光场时栅位移传感器测量原理最后的行波信号与相位有关，相位上的轻微变化将通过测量系统中比相部分给测量引入误差。通过分析，对相位影响的主要有运动方向(X方向)上接收透光面的变化、移相电路以及过零比较器等。其中运动方向上接收光斑的变化主要因为光源的散射影响，移相电路的影响主要取决于电路对移相的精确控制，过零比较器部分的影响主要与行波信号的幅值有关，幅值的变化则是由于光源的散射导致各部分接收到的透光面幅值发生变化和光源的均匀性造成的影响。结合上述分析得到光源散射从相位和幅值两方面对测量存在影响，因此，接下来对光源散射引起的变化进行详细分析。测量装置见图2(a)，光源以一定角度照射，光线经过动定尺(玻璃制成)发生折射，在运动方向(X方向)的分析如图2(b)所示，在垂直运动方向(Y方向)的分析如图2(c)所示。由图2(b)可以看出X方向的散射对各区域透光面栅距造成影响，Y方向散射对各区域透光面幅值造成影响。

图2 散射角误差模型

根据图2(b)可知理想光源下接收面接收的光斑宽度为W，但在散射角的影响下光斑宽度为Mi。

Mi=W+ΔWl-ΔWr

(2)

其中ΔWl、ΔWr为散射光源下的偏移量，可知4个区域的透光面都存在栅距上的变化，且4个区域接收光斑宽度不一致，使4路驻波信号相位变化。同样，图2(c)得到理想光源下光斑幅值长度为2A，但由于散射角使得光斑幅值变化为2Aj。

2Aj=2A+ΔA1-ΔA2

(3)

其中ΔA1和ΔA2为幅值上的偏量，由图2(c)得知4个区域透光面都存在其影响，且4个区域散射角造成的光斑幅值不一致，使四路驻波信号幅值发生变化。因此，当图1中动定尺在移动方向上运动时，0°、90°、180°、270° 4路透光面面积变化为：

(4)

式中M0°、M90°、M180°、M270°、A0°、A90°、A180°、A270°为散射角导致各区域透光面的实际栅距和实际幅值。

为便于对栅距和幅值引起的变化进行分析，将栅距变化和幅值变化分开处理。在只考虑光源散射的情况下各区域透光面的栅距发生的变化，将各透光面不同的栅距变化带入测量原理的推导中，得到式(5)行波信号表达式，式(6)是行波信号中与时间无关的分量，式(7)是只与时间有关的分量，行波信号的第3部分则是推导出来与时间和空间相关的分量。同样，在只考虑光源散射的情况下各区域透光面的幅值发生的变化，将各透光面不同的幅值变化带入测量原理进行推导，得到行波信号式(10)，式(10)中的第3项为与时间和空间都有关的分量，而式(11)、式(12)分别是与时间无关和与时间有关的分量。

(5)

Ua=A(M0°-M90°-M180°+M270°)+k(S-T)

(6)

(7)

(8)

(9)

(10)

U1=(A0°-A90°-A180°+A270°)W+Ka-Kb

(11)

(12)

(13)

(14)

式中k=4AW/π。

对栅距变化引相位变化的行波信号式(5)进行误差分析，在此情况下会引入直流分量，当M0°=M180°且M90°=M270°时的一次谐波误差，以及当四路不等时的二次谐波误差。对幅值引起的变化的行波信号式(10)进行分析，发现幅值不一致时会引入直流分量，以及当A0°-A180°=A90°-A270°时引入一次谐波误差。通过分析确定，当各区域透光面的栅距和幅值发生变化时会产生一次和二次谐波误差的叠加误差。

结合分析对其进行仿真，设置光源距接收面L=8 mm、动定尺距离δ=0.7 mm、动尺栅距W=0.1 mm，定尺栅距2W、透光面幅值A=0.1 mm进行建模。以0.004 mm的步距对单周期进行仿真，仿真行波信号及其误差频谱分析如图3所示。

(a)仿真行波信号

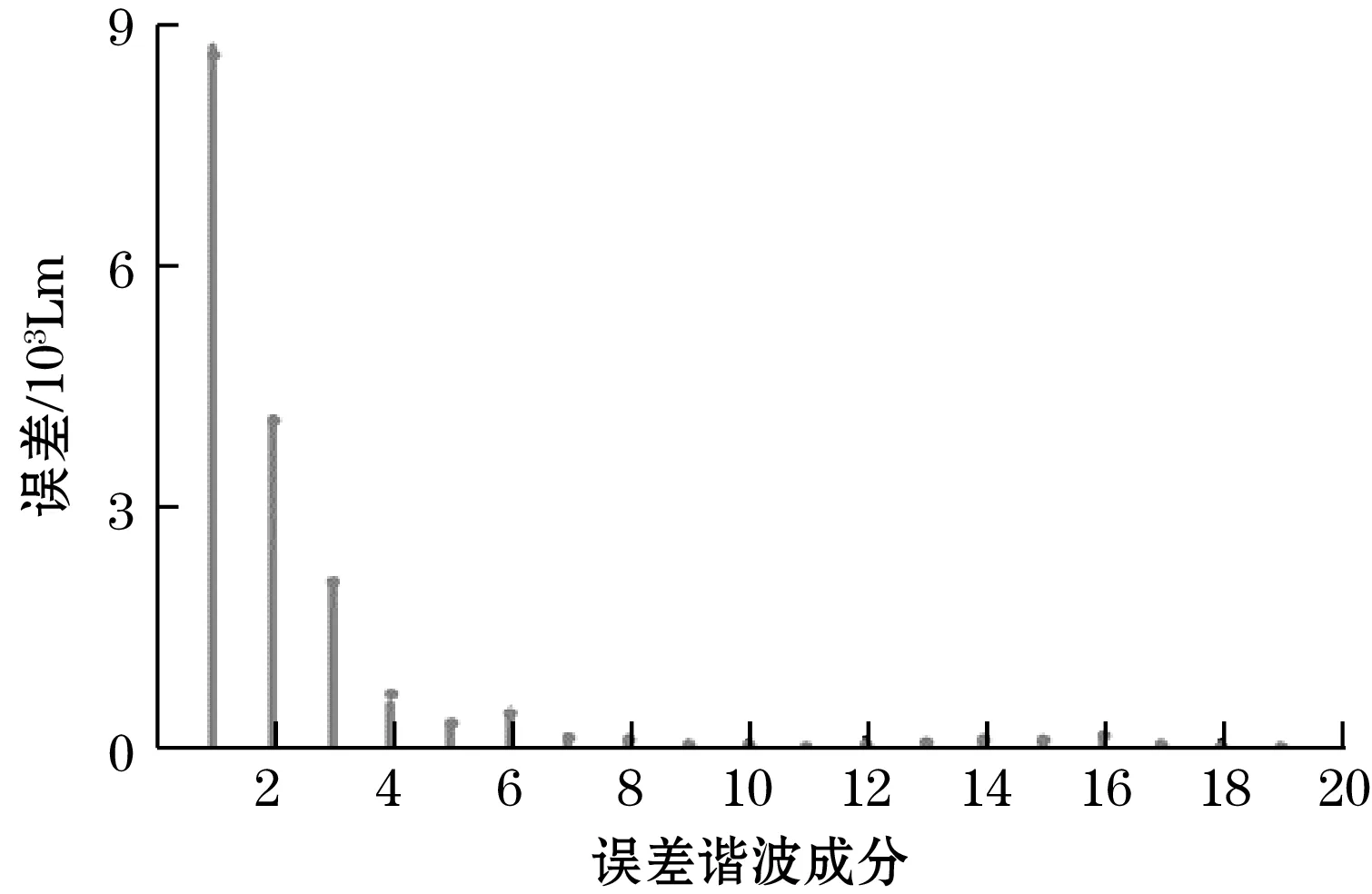
(b)仿真频谱分析

由图3(a)行波信号可知，行波信号的幅值不断变化与理想效果相差明显，同时行波信号的分布疏密不均与在等间距仿真的条件下均匀分布存在明显区别，这与式(5)和式(10)得到对行波信号的幅值和相位存在影响一致。由图3(b)误差频谱分析可知，此光源下误差成分主要为一次和二次谐波误差成分，其中一次和二次误差明显，这与前面散射误差模型中的推论一致。

3 准直光源优化设计

根据光场式时栅位移传感器测量原理，在原理推导时采用的是平顶光束光源[14]，可以将光照范围内的光强视作一个定值。但是在实际实验中采用的是LED芯片光源，LED芯片光源本身是近似的朗伯光源[15]，在任意方向上的光线均匀，这与平顶光束光源存在很大差距，给实验带入误差。通过对单光场分布分析建立光源散射角的误差模型、进行理论和仿真分析，可知光源散射角对传感器有一定影响。针对上述问题，结合散射角误差模型提出对光源空间进行约束的优化方法。因此，采用对光线具有约束作用的准直透镜来实现对光源散射角误差进行优化，将光源视为点光源，初始的球面半径、曲面与Z轴交点以及到接收面的距离已知，建立图4所示准直透镜示意图。

图4 准直透镜示意图

若空气折射率n0=1，透镜折射率为n，若将光源发出光线与球面交点为P(xp,yp)，与曲面的交点为Q(xq,yq)，光源光线从径向射入球面没有发生改变，但从曲面出射时在射出面上发生折射现象，对光线进行约束。根据折射定律：

(15)

(16)

(17)

在由法向量可以得到P点的切线斜率kp，进一步得到P点的切线方程。

(18)

yn+1=kp(xn+1-xn)+yn

(19)

yn+1=tan(θn+Δθ)·xn+1

(20)

将式(19)与式(20)联立，初始值L=8 mm、t=3 mm、r=3 mm、n0=1、n=1.49和Δθ=0.01°得到θ=0.01°时球面和曲面曲线上的第1个点，然后将其共同带入式(18)计算切线方程斜率，然后将其与计算斜率所利用点带入式(19)、式(20)得到下一个数据点，以此类推就可以得到曲线在此条件下所有的数据点，在此情况下得到的曲面是一个非球面，为便于加工对得到的曲线数据点在理论计算满足实验光斑条件的范围内进行拟合建立仿真模型，仿真如图5所示。

(a)朗伯型光源仿真图形及光强分布 (b)实际光源仿真模型及光强分布 (c)优化光源仿真模型及光强分布图5 朗伯型光源、实际光源、优化光源仿真及结果

其中图5(a)为朗伯型光源仿真图，可以看出朗伯型光源的光线是发散的，但实际做实验所用的LED芯片光源存在一定大小。在仿真中进行朗伯型光源配光得到图5(b)所示光强分布观察得到边缘光线较朗伯型光源相差较明显，但在发散半角±40°的范围光强分布与朗伯型光强分布较相似，所以在中间光斑区域可以近似视为朗伯型分布。因此，在朗伯型光源仿真图的基础上增添了透镜模型得到如图5(c)所示的优化光源仿真模型，可以看出光源光线经过透镜模型之后大部分的光线改变了原有光线的前进方向，其中透镜模型中对其处理部分是按照实验所需光斑的大小的2倍修改，将45°发散角之外的部分去除，在实际情况下没有对信号产生影响。透镜模型用有机玻璃制作，透光率在90%以上，透光效果整体有所降低但不会造成部分影响，因此对实验影响不大。从仿真结果上可以观察到朗伯型光源光束向不同方向发散得到的发光半角在±60°的范围，经准直透镜优化后的光源其发散方向有了明显的变化，其中大部分的光源光线经透镜之后光线按准直方向进行改变与理论一致，但在透镜外部出现了极少部分杂光，从仿真结果中可以观察的这部分杂光中大部分没有投射到接受区域上，对接受区域影响较小。总体来看经过优化的光源在接受区域部分的发光半角在±10°的范围内，因此从仿真模型可以确定通过上述方式可以达到减小散射的目的。

4 实验验证

在理论模型和仿真模型分析的基础上，对上述分析过程进行实验验证，利用驱动电路板驱动光源产生交变光场，交变光场通过动定尺的空间调制，在接收装置区域获得8组光电流信号，在经过后面的电路处理得到行波信号。实验中动尺栅距W=0.1 mm的矩形透光区域和不透区域，定尺周期2W=0.2 mm余弦透光面。搭建了如图6所示的实验平台。

图6 直线时栅位移传感器试验台

图6中，观察到未添加透镜的LED芯片光源光斑发散较广且中间亮度最亮逐渐向周边减少，而经过优化的添加透镜光源光斑比未添加时亮度大，且中间区域在满足透光面大小的情况下亮度变化没有边缘区域变化明显。

利用精密直线导轨平台以0.005 mm步距移动，对单周期进行测试，利用RENSHAW XL-80激光干涉仪测量值作为参考，用驱动电路板驱动LED芯片光源产生交变光场。采用图6中未优化的光源进行实验验证，得到经误差修正的测量误差如图7所示。

从图7中可以得到单周期内未进行光源优化系统的测量误差为±5.6 μm，主要误差成分为一次、二次谐波误差，这与之前的仿真误差频谱分析结果一致。然后利用图6中添加透镜的光源进行同样的测量和处理，得到图8所示的误差曲线。

由图8的可以看出增添透镜的单周期测量误差在±1 μm，主要误差成分为一次和二次谐波误差。对上述结果进行分析，从测量结果可以看出增加透镜的测量误差相比较于为优化光源的测量误差明显有所减小，一次、二次谐波误差皆有所减小，其中一次谐波误差减小最明显，实验证明采用对光线约束的方式具有优化效果，因此对优化过后测量系统进行长周期测量，取步距为0.2 mm，对100 mm范围周期进行测量得到如图9所示的误差曲线。

(a)测量误差曲线

(b)误差频谱分析图7 未优化光源测量误差分析图

(a)测量误差曲线

(b)误差频谱分析图8 增添透镜的光源误差分析图

图9 100 mm长周期测量误差曲线图

从测量结果可以看出，在100 mm测量范围内测量误差控制在±8 μm以内，且以低频线性误差为主，这种误差主要由传感器安装和加工造成，为传感器运行过程中的固定误差，通过误差补偿可以将其影响消除。

5 结论

本文介绍单光场时栅位移传感器的测量原理，建立光源散射角误差模型和光源优化模型，进行理论分析和仿真验证，并进行试验测试。通过以上分析得到以下结论：

(1)通过建立了光源散射二维误差模型，理论分析了光源散射对测量精度的影响，仿真分析出对测量误差的影响为一次、二次谐波误差；(2)提出了光线约束准直透镜设计方法，开展光源散射约束的准直透镜研究，完成相关透镜理论分析及制作；(3)通过与未优化光源进行对比试验，实验结果验证了光源散射对测量误差影响分析的正确性，并通过所设计的准直透镜约束获得了较理想的测量结果，在栅距为0.2 mm，周期内误差从±5.6 μm减少到±1 μm以内，因散射引起的一、二次谐波误差得到明显抑制，在全量程100 mm测量范围内，测量误差为±8 μm，主要为安装与加工引起的线性低频误差。