基于EMD的城市轨道交通走行部轴承故障监测系统
2022-12-26苏燕辰李忠元
万 恒,苏燕辰,李忠元,吴 琛
(1.西南交通大学机械工程学院,四川成都 610031;2.中车青岛四方机车车辆股份有限公司,山东青岛 266111)
0 引言
近年来,随着经济的高速发展,逐步形成了以1 h通勤圈为基本空间范围的多个都市圈,城际列车成为都市圈通勤的首选。而交通首要的问题就是需要保证其安全,列车的轴承故障是引发列车事故的主要因素之一。
轴承故障诊断主要是通过安装在轴端的加速度传感器对采集的振动信号进行时频分析,如峰值法、峭度、傅里叶变换、小波分析等方法[1];由于列车走行部的滚动轴承发生故障时信号是非平稳的,其振动信号各频带的能量发生相应变化,可利用各频带能量分布作为该状态下轴承故障特征向量[2];传统的采用傅里叶变换通常应用于稳定信号而对于处理振动信号,其存在着一定的局限性,自适应的经验模式分解(EMD)和希尔伯特包络谱分析(Hilbert)相结合的分析方法[3],能够对列车运行过程中的振动信号进行故障特征提取。本文采用ARM3354为核心的处理器,选用复合传感器,其内置振动以及温度信号,通过对信号的处理设计出相关的算法,以ARM3354为主控芯片设计的城际列车的实时监测系统[4],实验结果与计算结果能够匹配。
1 系统的总体方案设计
ARM微处理器具有数据处理能力强和功耗低的特点,被广泛应用于各种场景,根据本方案的设计需求,选用ARM3354作为系统的主控芯片,同时选用Cortex-M4内核STM32F407作为的子系统的控制芯片。数据采集模块采用STM32F407,并对原始信号做预处理,使用ARM3354对预处理的数据进行算法分析,得到的数据通过内部网络发送给通信板卡,通过TRDP总线上传到TCMS,以实现系统对数据进行实时采集、分析、上传,可以通过上位机软件对系统进行参数配置,并且还可以使用地面系统对采集的原始数据进行数据对比、故障诊断、故障分析等,并将原始数据,经算法处理后的诊断数据以及报警数据存储到硬盘中,以实现一个完整的城市轨道交通走行部在线监测系统。图1为系统的总体框图。

图1 系统总体框图
2 系统硬件设计
2.1 信号调理和采集电路
高速列车运行速度快,因此分析的数据需求量以及数据的精度要求高。如图2所示,系统将传感器传入的电信号通过差分运算放大器传入AD7606数据采集模块。采用OPA2188AID芯片作为系统的运算放大器,OPA2188AID可在单电源±2 V或者双电源±18 V使用。 AD7606是一个16 位 ADC,所有通道都具有 200 KSPS的采样率,同时具有8通道同步采样的特性,满足系统需求。
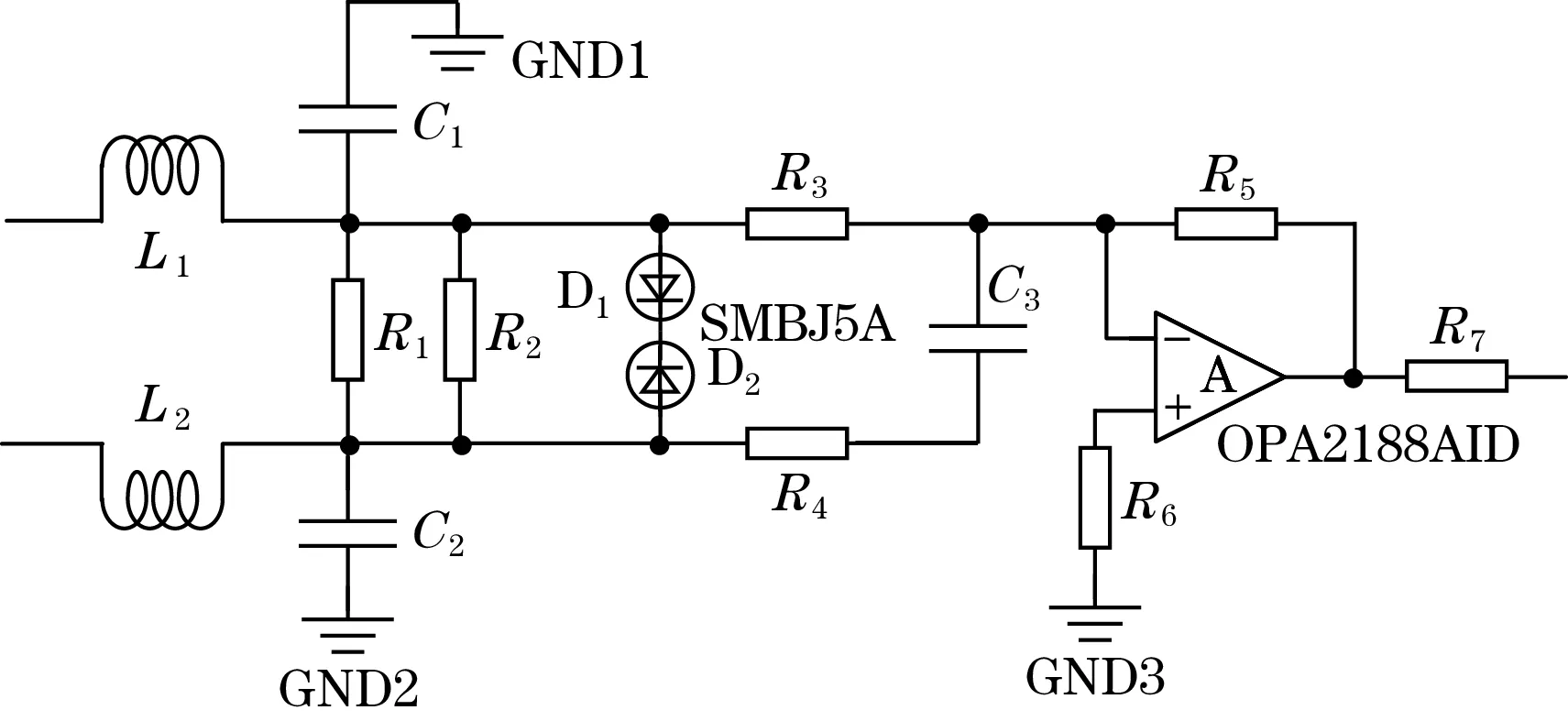
(a)信号滤波电路

(b)信号放大电路图2 信号滤波与放大电路
2.2 硬盘存储
系统每天运行在线时间长,存储数据量大,因此采用SATA硬盘作为存储介质,相比传统的IDE(ATA)和SCSI硬盘,SATA硬盘具有高速度、高容量、价格低、操作方便的优点。使用ARM3354记录板的USB1_DM和USB1_DP 2个引脚与TUSB9261芯片的USB_DN和USB_DP引脚相连。是一款具有自适应器的USB转SATA接口的桥接芯片,可以使接收获得更大的抖动容差。
3 监测系统软件设计
系统采用AD7606作为数据采集模块,该芯片不仅具有高性能、低功耗以及抗干扰的优点,并且具有灵活的并行/串行接口,可以满足本系统的数据传输要求。如图3所示,设定系统采样频率,通过定时器中断触发完成ADC采样,当数据采样达到1个周期的采样数,通过SPI总线将采集的数据发送给处理板,处理板对原始信号进行经验模态分解,对每一层的IMF分量进行分析,选取最优的本征模态函数,然后进行Hilbert变换,对变换后的信号进行取模包络,通过FFT确定轴承的故障频率以及幅值,最终通过幅值计算信号的特征值,若超过阈值,则将报警信息通过TRDP协议传输到TCMS上,对应得到报警标志位置1报警[5],图3所示为软件算法流程图。

图3 软件算法流程图
4 轴承故障诊断原理
本设计采用的经验模态(EMD)分解,与小波分析不同,EMD是一种自适应的信号处理方法。小波分析法处理信号之前,需要选定小波基,其在信号分析处理过程中不能更改,因此即使选定的小波基对于全局数据来说是最优的,但是相对于局部而言,则不一定。EMD分析一段未知的信号之前,不需要提前对信号进行分析,能够自适应的将原始信号分成多层的本征模态函数(IMF)和残余信号。
4.1 经验模态变换(EMD)
EMD算法可以根据信号本身的不同尺度和趋势逐级对其进行分解,从而得到一系列具有不同特征尺度的IMF[6],而每一层的IMF对于原始信号的相关度都不同。EMD算法步骤如图4所示[7-8]。

图4 EMD算法步骤
图4中IMF需要满足2种条件:极值点数目与零点个数差值小于等于1;任意数据段,局部上包络线e+(t)和下包络线e-(t)相对于时间轴局部对称。
其中m(t)为均值包络线,r(t)为中间信号,cn(t)为第n个满足IMF 2个条件的信号。最终的单调函数或者常量为残余量,记为Res。
EMD分解的信号满足:
(1)
式中:x(t)为原始信号;cn(t)为1到n阶IMF分量;Res为残余分量。
4.2 希尔伯特变换(Hilbert)
EMD分解后的ci(t)信号,计算ci(t)的相关系数并存在数组A中,计算出相关系数的最大值R以及在数组中的位置C,对其经过Hilbert变换得到:
(2)
解析信号:
zi(t)=ci(t)+jH[ci(t)]=ai(t)ejφi(t)
(3)
ai(t)为幅值函数,其表达式为
(4)
φi(t)表示瞬时相位,表达式为

(5)
ωi(t)表示瞬时频率,表达式为
(6)
根据解析表达式可知,振动信号经过Hilbert变换得幅值包络,根据式(4)可以得到原始振动信号的包络图。
5 故障诊断验证
本文实验室验证数据采用6205-2RS SKF深沟球轴承,通过在轴承支座上方的加速度传感器采集振动数据,其中振动频率为12 kHz,电机转速为1 797 r/min,故障直径为0.178 mm,压力角α=0,其轴承参数如表1所示,将数据导入到监测系统的采集板,模拟数据采集,数据采集模块通过SPI总线将轴承数据传输到处理板进行数据处理。

表1 轴承参数表
根据对应的参数可求得轴承的故障频率[9]。轴承内圈的故障频率为
(7)
轴承外圈的故障频率为
(8)
式中:N为轴承滚动体的个数;d为滚动体直径;D为节径;fr为轴的转频。
分别取轴承内圈和外圈在1 s时间的信号,如图5所示,分别为轴承内圈和外圈原始信号时域和频域图;从频域图可以看出内外圈的故障信号不能被准确找到,故障信号被大量的噪声淹没。
使用EMD将原始信号分解,分别得到6个IMF,其波形如图6、图7所示。在EMD分解后,求出每一层IMF与原始信号的自相关系数,其相关系数如表2、表3所示。
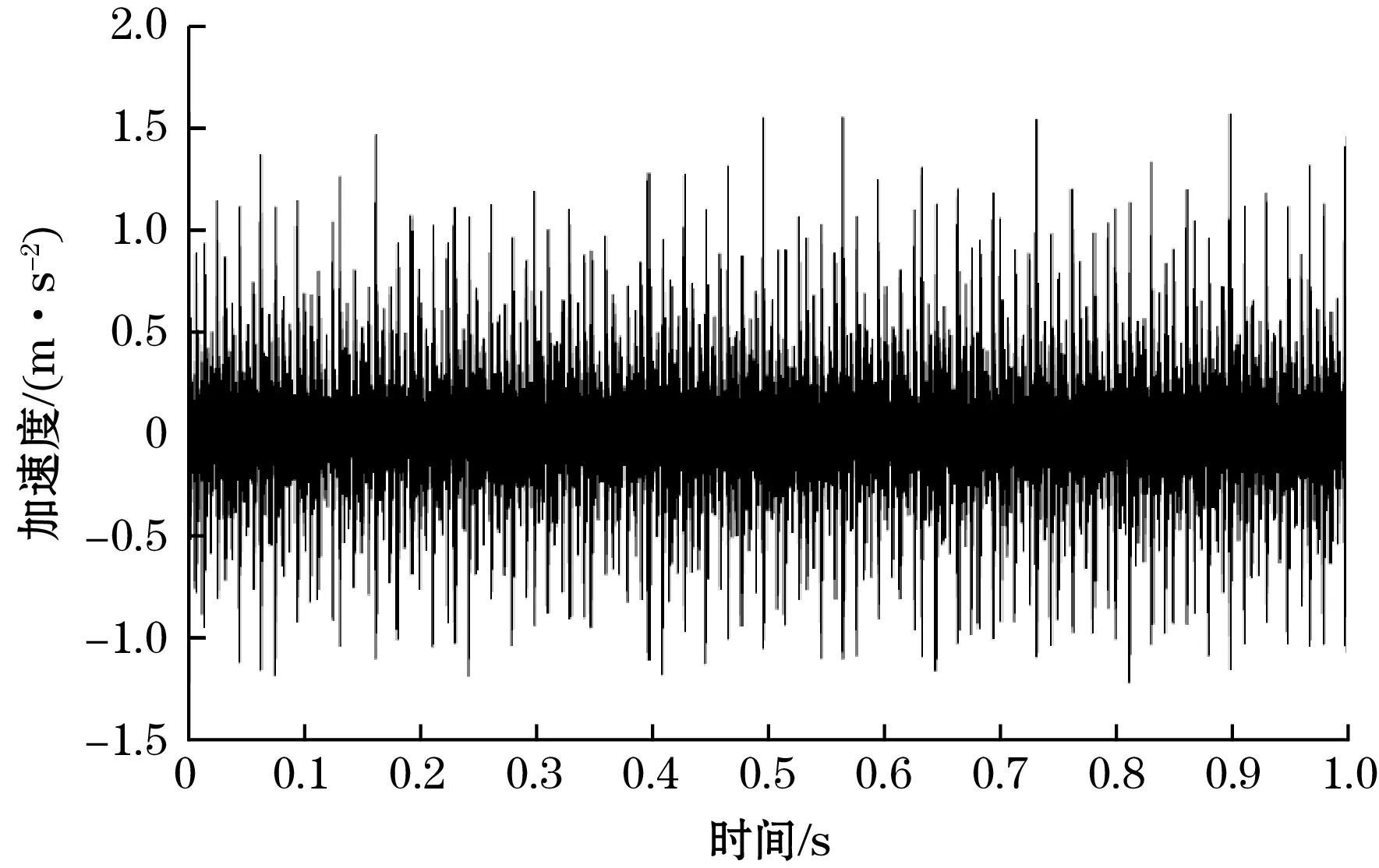
(a)内圈原始数据时域图

(b)内圈原始数据频域图

(c)外圈原始数据时域图
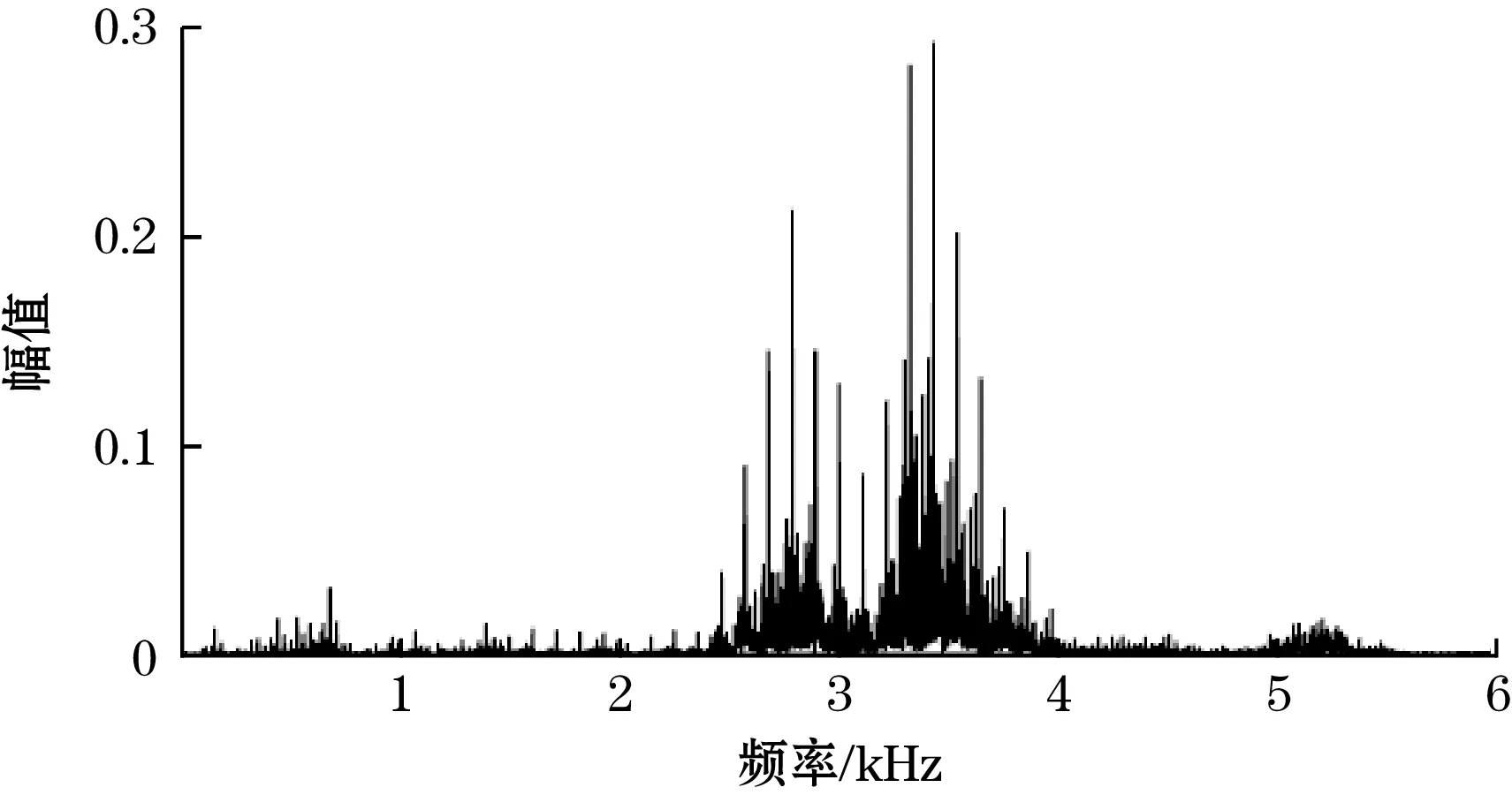
(d)外圈原始数据频域图

图6 轴承内圈EMD分解信号

表2 内圈IMF自相关系数

表3 外圈IMF自相关系数
由表2、表3可知,IMF1的自相关系数分别为0.94和0.92,因此选取IMF1作为信号的有效分量,经Hilbert变换得到有效信号的包络,最后通过FFT变换后找出轴承的故障频率,如图8所示。
分别计算出内圈的故障频率为162.2 Hz,外圈的故障频率为107 Hz。由图8 (a)可以看出,经EMD分

图7 轴承外圈EMD分解信号

(a)轴承内圈包络频域图
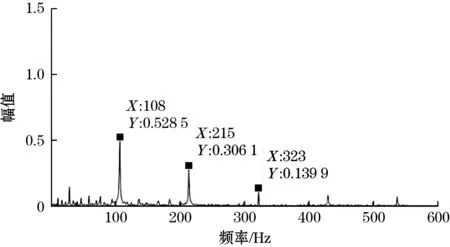
(b)轴承外圈包络频域图图8 轴承故障包络频域图
解以及Hilbert变换求出的故障频率为162、323、485 Hz;由图8(b)可以看出内环故障频率为108、215、323 Hz。由此可以看出系统可以准确找出轴承的故障频率以及其倍频。
系统的评价指标为
(9)
式中TZ为幅值。
根据阈值大小,将报警值等级分为预警,一级和二级报警,通过通信板实时将报警数据发送给TCMS。
6 结束语
系统以ARM为主控芯片,通过EMD和Hilbert变换,对复杂的轴承振动信号通过自适应的故障提取方法,在实验的基础上,准确找到轴承的故障频率,并能够实时地通过通信板发送给TCMS,以实现对列车运行过程中走行部轴承状态的实时监测,系统稳定可靠,使用简便,为城市轨道列车的安全运行提供了保障。
