改进PointNetLK的点云智能配准与位姿图优化方法
2022-12-26李荣华董欣基薛豪鹏祁宇峰张建禹
李荣华,董欣基,薛豪鹏,祁宇峰,张建禹
(大连交通大学机械工程学院,大连 116028)
0 引 言
空间非合作目标构型重建是位姿估计、姿态跟踪[1-2]及在轨捕获等关键环节的基础,在故障卫星维护及废弃卫星清理等在轨服务中发挥极其重要的作用[3]。空间非合作目标构型重建主要受目标可测部位点云数据质量和配准精度影响。单目相机与激光雷达都是常用的测量工具,考虑到空间抗干扰及光照影响等因素,单目相机具有缺乏深度信息、特征提取不稳定、适应性较差等缺陷[4-5],激光雷达是最为理想的空间非合作目标测量载荷[6]。使用激光雷达对目标进行扫描能够获取点云数据,因其能够以相对较低的存储成本获取较精确的物体拓扑结构和几何结构而受到了日益广泛的重视。在实际扫描过程中,由于被测目标尺寸过大、物体表面被遮盖或激光雷达的扫描角度过小等因素,单次雷达扫描中往往没有目标全部的几何信息,所以需要对两幅或多幅点云进行配准,以得到完整的几何信息。
Besl等[7]提出的迭代最近点(Iterative closest point,ICP)算法在点云数据配准领域中做出很大贡献。刘跃生等[8]为了防止离群值对配准的负面影响,提出了混合稀疏迭代最近点(SM-ICP)方法;王子玮等[9]为了克服稀疏ICP与稀疏最小切线距离(Tangent distance minimum,TDM)算法的局限性,提出了稀疏混合ICP算法;马鑫等[10]基于ICP与n点透视(PnP)算法的差异与联系,提出了RGB-D同步定位与地图创建系统(Simultaneous localization and mapping,SLAM)中2种PnP算法的切换策略,并在优化问题中根据观测的不确定性对各误差项赋予不同权重;刘智远等[11]基于局部凸连接补片(Locally convex connected patches,LCCP)点云分割算法与点云Harris关键点,在已知目标外轮廓点云的基础上,提出了一种ICP初始迭代位姿获取方法;李绕波等[12]提出一种利用重心特征变换处理来解决不同场景点云空间特征约束下的点云空间配准方法;Marchel等[13]基于误差建模的三个原始加权因子,对ICP环境扫描匹配的标准进行修改。当前算法的单向迭代机制易出现因误差在同一方向上积累导致的配准精度降低,甚至陷入局部最优解,使配准失败的问题。而对于使用神经网络,Charles等[14]提出的PointNet算法为第一个采用对称函数方式、直接输入点云数据的一个端到端的神经网络;在PointNet神经网络的基础上,Yasuhiro等[15]引入传统光流法(LK),提出了PointNetLK点云配准神经网络;何凯等[16]提出一种基于混合注意力机制和相关性估计网络的点云配准算法。当前算法解决空间非合作目标可测部位点云带来的无先验信息、目标描述不完全的点云配准问题时仍有精度较差、效率不高的问题。
本文提出一种面向空间非合作目标的点云智能配准算法。在使用半物理仿真平台对空间非合作目标进行扫描后,进行目标提取,剔除场景中散乱目标和噪声,并对PointNetLK神经网络配准算法进行改进,将处理后的点云数据作为改进后的智能配准算法的输入,后端对配准结果进行位姿图优化,得到空间非合作目标的相对位姿。
1 Straight Through滤波目标提取算法
在进行半物理仿真地面试验时,由于空间限制,激光雷达对空间非合作目标进行扫描,往往会因为背景信息杂乱,提高数据处理的复杂程度。故在点云配准算法前端对原始目标进行目标提取。
采用Straight Through滤波算法,通过对点云三个维度的范围限定,对采集到的数据进行预处理。设定采集得到的原始目标点云集为P={P1,P2,P3,…,Pn},其中任意一点Pi的坐标为Pi=(xi,yi,zi),xi∈X0,yi∈Y0,zi∈Z0。
通过结合半物理仿真实验平台、非合作目标主体尺寸在不同姿态下的x,y,z三个方向的最大值和最小值,确定三个方向的阈值范围xmax,xmin,ymax,ymin,zmax,zmin,对维度范围内的点云进行快速提取。提取后的第i帧点云集为Pt={P1,P2,P3,…,Pm},m (1) 一般深度学习神经网络模型对于图像等规范化的输入,易获得较好的输出,而点云相对于图像有个十分突出的特点,即无序性,这也对网络设计提出要求。为了克服无序的特点,可引入通过对称函数的数学计算把每个点的数据进行整合的方法。 PointNet算法的网络结构如图1所示,输入由n个具有三维坐标信息的点所组成的点云数据。PointNet以点的数量n为二维卷积的高度,三维坐标为宽度。为面对空间非合作目标时仍有一定的高效率与高精度,同时保留各点的信息,利用权重共享的MLP(64,64)进行特征提取之后,再利用平均池化层压缩数据大小,在获得部分点的32维特征之后,再继续使用MLP,得到2048维特征,最后利用平均池化层获得点云的全局特征向量,将其通过全连接层附加在32维特征后面,经过分类器得出点的预测得分。 图1 PointNet架构Fig.1 PointNet architecture G-1=exp(-ξ∧) (2) 式中:ξ是李群G对应的李代数;n∧表示将向量转化为反对称矩阵。 三维点云配准问题则为找到G-1,使得: (3) 将式(2)进行一阶泰勒展开得: (4) 通过添加左扰动ΔT=exp(δξ∧)求得: (5) 此时将式(4)变形得到: (6) 式中:J+是J的伪逆。 (7) 最后的估算值Gest是迭代循环中计算的所有增量估算值的组合: Gest=ΔGn·…·G1·ΔG0 (8) 迭代的停止判据为ΔG小于设定的最小阈值ΔGth。以上模型流程如图2所示。 图2 PointNetLK流程图Fig.2 Flow chart of PointNetLK 由于空间非合作目标没有先验信息,无法提供真实变换矩阵Ggt,故损失函数应重新设定。损失函数的目标是使配准结果点云和目标点云中对应点之间的距离最小化。所以使用式(9)表示损失函数。 (9) 配准结果如图3所示,在空间非合作目标可测部位点云配准中,改进的PointNetLK点云智能配准算法会得到较高精度的配准结果。其中,红色的、点最小的为源点云;蓝色的、点较小的为目标点云;绿色的、点最大的为配准结果。 图3 改进的PointNetLK算法配准效果Fig.3 The registration effects of an improved PointNetLK algorithm 由于ModelNet40中各类别的数据之间大小不同、位姿随机变化,所以在初始PointNetLK算法中,无论是训练或是测试过程中,都以数据集的每个点云为目标点云,随机生成或手动添加变换矩阵Ggt,将目标点云集整体施加Ggt得到源点云集,最后将目标点云与源点云配准。 而在空间非合作目标点云配准中,采集到的点云模型大小统一、运动状态规律,并且无法提供有效的先验信息即变换矩阵Ggt,所以配准方式需要改变。将采集到的点云数据按照采集顺序编号i(i=0,1,2,…,n),从i=0开始索引得到目标点云集,再从i=1开始索引得到源点云集,最后将目标点云与源点云配准n次,得到n个各帧之间的相对位姿。 在点云数据配准完成后,往往配准存在误差,因此在配准算法后端链接位姿图优化,达到提高配准精度,进而提升后续重建质量的目的。 图由点与边组成,以点代表优化变量,边代表误差,其优化变量即是各帧间的相对位姿。 首先定义相对位姿李群表达形式如下: (10) 式中:Ti,Ti+1为第i帧和第i+1帧的位姿;Ti(i+1)为第i帧与第i+1帧之间的相对位姿。 其李代数形式为: exp(ξi+1)∧)∨ (11) 所以误差表达式为: exp((-ξi)∧)exp(ξi+1)∧)∨ (12) 为得到ei(i+1)关于ξi,ξi+1的导数,对其添加左扰动,得到: exp(δξi+1)∧Ti+1)∨ (13) 根据变换群伴随性质: exp(ξ∧)T=Texp((Ad(T-1)ξ)∧) (14) 得到: (15) 式中: (16) 得到了误差关于优化变量的导数。 将所有误差项相加得到总体目标函数为: (17) 可以采用高斯-牛顿法来解决后续的图优化问题。假设初始量为xk,Δx为在初值附近的微小增量,k为迭代次数,则误差为ek(xk+Δx),对其进行一阶泰勒展开得: ek(xk+Δx)≈ek(xk)+JkΔx (18) 式中:Jk为误差函数ek在xk附近的导数,即雅可比矩阵。 因此,对于第k个误差函数得目标函数为: (19) 式中:ek,bk,Δx都为列向量;Ck表示该边在变化前的取值;Hk为高斯-牛顿法中对于海塞矩阵的近似。 目标是找到使得增量最小的Δx,所以直接令Fk(xk+Δx)对Δx的偏导数为0,得: (20) 考虑所有边,得到增量方程: HΔx=-b (21) 综上,关于位姿图优化问题,首先给定一个初值x0,然后计算雅可比矩阵J(xk)与误差e(xk),并计算增量方程,如果所得到的结果Δxk小于预定阈值,则终止迭代,否则令xk+1=xk+Δxk,重新计算。最终得到使得误差最小的相对位姿。 使用半物理仿真平台,通过线阵激光雷达扫描空间非合作目标获取多帧目标的可测部位点云,验证本文算法相对于传统ICP算法在效率和精度方面的提高效果。 应用Pycharm Community Edition 2021,Visual Studio 2019,点云库(Point cloud library,PCL)与GTSAM库,实验系统基本参数为:Windows 10系统,Intel CORE i5-8300处理器,NVIDIA GTX 1050 Ti显卡,16 G内存。 根据任务要求和技术指标,任务的技术指标:配准平移距离误差为±5 mm,旋转角度误差为±5°,半物理仿真实验缩比为1∶10,运动状态为自旋运动,雷达扫描帧频率为1 Hz,目标运动时长约为100 s,即得到101帧点云数据。在线阵激光雷达可完整捕捉非合作目标的条件下,非合作目标外形可完整获得。 采用激光雷达对模拟的空间非合作目标进行扫描,由于环境的复杂性,获得的点云数据包含环境中的其他目标,如图4所示。采用Straight Through滤波算法对点云数据进行滤波,经过计算与实验,得到包含模拟空间非合作目标的最小长方体,提取出空间非合作目标点云,如图5所示。 图4 半物理仿真试验系统扫描结果Fig.4 Scanning results of semi-physical simulation test system 图5 空间非合作目标提取结果Fig.5 Results of spatial non-cooperative object extraction 在进行配准前,首先要对智能配准网络进行训练,将激光雷达对各种物体在不同工况下运动扫描所获取的点云数据制作成训练集;将半物理仿真实验平台得到的点云数据制作成测试集,其中三轴平移距离真值为0 mm,围绕X,Y,Z轴线的旋转角度真值分别为15°,20°和25°。 图6 本文算法与ICP算法平移量对比Fig.6 Comparison of translation between the proposed algorithm and ICP algorithm 表1 配准平移误差统计Table 1 Registration translation error statistics 图7 本文算法与ICP算法旋转量对比Fig.7 Comparison of rotation between the proposed algorithm and ICP algorithm 为进一步证明本文算法的高精度性,与文献[9,12,16]所提出的算法进行比较。比较效果见表3。 综上所述,本文算法的三轴平移距离优于ICP算法,但略低于其他算法;旋转角度明显优于ICP与其他算法;在三轴平移距离误差为±5 mm以及三轴旋转角度误差为±5°的容忍范围内,本文算法在三轴平移距离误差、旋转角度误差上优于ICP算法。 表2 配准旋转误差统计Table 2 Registration rotation error statistics 表3 算法精度对比Table 3 Comparison of algorithm accuracy 本文算法与其他算法配准耗时结果见表4。 表4 算法耗时对比Table 4 Comparison of algorithm time consumption 由表4可知,本文配准算法耗时略优于文献[8]所提算法,明显优于文献[7,10,12]所提算法。 在配准之后对配准得到的相对位姿进行位姿图优化,以第0帧为基准,空间非合作目标的位姿为点,位姿之间的关系即变换矩阵为边。经过位姿图优化后的三轴平移与旋转误差见表5。 表5 配准误差统计Table 5 Registration translation error statistics 根据平移距离和旋转角度对整体运动的影响作用,较好旋转角度会导致平移距离误差降低,因此对六个参数误差都赋予了权重,其中三轴平移距离权重均为1/9,三轴旋转角度权重均为2/9,综合描述配准效果。本文智能配准算法综合误差为1.7291,ICP算法为6.3598。与ICP算法相比提高约72.81%,整体配准效果有较大提升。在效率方面本文智能算法优化部分耗时为4 s,整体耗时为420 s,ICP算法整体耗时为3316 s,效率提升约87.33%。 为验证本文智能配准算法的鲁棒性,现增加对不同工况与不同噪声下目标的配准实验。 改变模拟目标工况,设定多组实验,每组实验对象工况三轴平移距离为0 mm,三轴旋转角度见表6。 表6 各组工况Table 6 Working conditions of each group 重复4.1~4.3节的实验,实验结果分析见表7~8,配准结果可视化如图8所示。其中,红色的、点最小的为源点云;蓝色的、点较小的为目标点云;绿色的、点最大的为配准结果。 表7 各不同工况组实验结果误差Table 7 Error of experimental results of different working conditions 表8 各不同工况组实验结果均方根误差Table of experimental results of different working conditions 由此可得,本文算法在针对不同工况的空间非合作目标点云配准时,仍可获得较好稳定性与较高的配准精度。 再次对目标施以不同程度的高斯噪声,噪声程度如表9所示。 再次重复4.1~4.3节的实验,实验结果分析见表10~11,配准结果可视化如图9所示。其中,红色的、点最小的为源点云;蓝色的、点较小的为目标点云;绿色的、点最大的为配准结果。 表9 各组噪声程度Table 9 Noise level of each group 实验结果表明,本文算法在面对不同工作状态下与不同程度噪声下的空间非合作目标可测部位点云配准时,尽管综合误差等有所波动,但是有较好稳定性,且仍然在任务的技术指标允许范围内,因此本文算法具有较好鲁棒性。 图8 各不同工况配准结果Fig.8 Registration results of each working condition 表10 各不同程度噪声组实验结果误差Table 10 Error of experimental results of different noise groups 表11 各不同程度噪声组实验结果均方根误差Table of experimental results of different noise groups 图9 各不同程度噪声组别配准结果Fig.9 Registration results of different noise groups 本研究以解决空间非合作目标位姿测量问题为主要目的,提出了一种面向空间非合作目标的点云智能配准算法,针对空间非合作目标没有先验信息的特点对PointNetLK算法进行改进,并在配准后对配准结果进行位姿图优化。在平移距离累积误差为±5 mm、配准旋转角度累积误差为±5°的条件下,验证本文算法的配准精度与效率,使用本文智能配准算法与ICP算法进行对比实验,配准综合误差较ICP算法从6.3598降低到1.7291,约提升72.81%,可有效提高配准精度;单次耗时较ICP算法从33.16 s降低到4.2 s,约提升87.33%,可有效提升配准效率。与其他算法相比,精度与效率也略有提升。并且在不同工况与点云数据存在不同程度的噪声时,仍有较好的鲁棒性。为解决空间非合作目标相对位姿测量难题以及配准算法的实际应用提供了技术支持。2 改进PointNetLK的点云智能配准算法
2.1 改进架构的PointNet算法

2.2 改进损失函数的PointNetLK算法




2.3 非合作目标配准方式
3 位姿图优化
3.1 位姿图优化问题构建


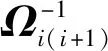
3.2 基于最小二乘法的位姿图优化
4 空间非合作目标仿真智能配准实验
4.1 空间非合作目标提取


4.2 智能配准实验







4.3 位姿图优化

4.4 鲁棒性测试








5 结 论
