临近空间高超声速稀薄流中梯形缝隙绕流分析

李舟波，方蜀州

(北京理工大学宇航学院，北京 100081)

0 引 言

航天器的表面实际上存在很多不连续的情况，不同几何形状的缝隙经常出现在各种气动表面上，如航天器壳体、燃气轮机通道、热交换器和微电子芯片中的肋状表面[1]。近年来，缝隙结构更被广泛应用于超燃冲压发动机，以延长超音速空气和喷油在燃烧室中的停留时间[2]。但是，缝隙结构会严重影响气流的流动状态与传热特性。这是因为在缝隙入口处由于边界层分离与再附将产生局部高热流区；在某些工况下缝隙入口处会产生激波；缝隙内会卷起旋涡结构等。同时，旋涡结构会向缝隙中卷入大量热量，使得传热特性由热传导变为热传导加对流传热，缝隙壁面热流随之大大增加。因此，高超声速飞行器表面缝隙的流场结构和热流分布受到了广泛的关注。近年来，国内外许多研究者对缝隙进行了各种数值和实验研究[3-15]。

Sudarshan等[3]研究了圆形和抛物形缝隙的传热变化和内部激波特性，在马赫数分别为 10.9和 10.2 的高超声速风洞中进行了实验。结果发现，缝隙结构使机头表面的热通量大幅减少，这对缓解气动加热是非常有效的。Dhankarghare等[4]将支板组合成一个支板缝隙，并在不同马赫数和长径比的情况下，将其与壁面缝隙进行比较。结果表明，两种缝隙在马赫数和宽高比较低时都表现出内部压力振荡，而在高马赫数和宽高比时振荡减小。Krishna等[5]通过实验研究了在超声速条件下，矩形缝隙后壁面几何形变的影响。研究表明，缝隙壁面坡道结构使得缝内整体声压和脉动压力分别降低了10 dB和50%。

国内方面，王世芬等[6]、唐贵明[7]分别在激波风洞上开展了缝隙热流测量实验，研究了平板上的矩形缝隙和单个横缝内的热流分布。张昊元等[8]针对高超声速飞行器前缘防热瓦结构，通过求解三维可压缩Navier-Stokes方程进行了数值模拟，研究了缝隙诱导形成的三维旋涡的空间分布特征和旋涡运动对物面气动加热的影响规律。肖志祥等[9]通过数值求解雷诺平均的Navier-Stokes方程组，数值模拟导弹跨、超声速流动，研究导弹环向凹槽等典型分离流动的被动减阻措施对阻力缩减的影响。通过分析计算结果发现环向凹槽有利于降低摩擦阻力，但底阻减小不明显。陆海波等[10]对高超声速飞行器鼻锥使用迎风凹腔结构作为热防护系统时，凹腔结构的防热效能进行了数值研究。结果表明迎风凹腔结构能够有效对高超声速飞行器的鼻锥尤其是驻点区域进行冷却，凹腔越深，其冷却效果越好。鼻锥气动加热的最大热流并不在尖锐唇缘的顶点，而是位于凹腔内的侧壁面上，凹腔的深度(L)变化对最大热流的出现位置影响很小。除非凹腔很浅(L/D<0.5)，凹腔底面的热流值都非常小，基本可以忽略。Wang等[11]通过风洞实验和数值计算，揭示了圆形缝隙可压缩流动的换热特性。在缝隙后缘附近热流比无缝隙模型显著增加，同时随着缝隙直径(D) 与深度(H) 之比的减小，缝隙内的升温幅度减小。

可以看到，在临近空间(60～100 km)中的高超声速缝隙结构的研究仍然很少，这可能是高超声速条件下可靠的实验数据测量困难和临近空间稀薄气体效应的原因。但随着计算机技术的发展，尤其是直接模拟蒙特卡洛(Direct simulation Monte Carlo,DSMC) 方法的计算效率增强，对稀薄缝隙绕流的研究也越来越多。Jin等[12]采用DSMC方法对一组具有圆形分离/再附角的二维矩形缝隙模型进行了高超声速稀薄流动数值模拟。结果表明，对于圆形分离角，外部气体分子更容易进入缝隙，从而促进了与缝隙内气体分子的动量和能量交换。而圆形再附角则会使得气体分子从缝隙内逸出，削弱动量和能量的交换。Guo等[13]采用直接模拟蒙特卡洛法,研究了带后掠角缝隙的流动特性，模拟条件为海拔高度20～60 km,马赫数 6～20。可以观察到，增加高度，缝隙内二次回流区的旋转方向会发生逆转。增加马赫数，缝隙内的速度、压力和温度均增加。Palharini等[14]采用DSMC方法研究了80 km高度稀薄过渡流区高超声速缝隙绕流问题，探索缝隙几何尺寸(长深比)对缝隙内部流场结构、壁面热流和压力的影响规律。结果表明，在80 km高度稀薄过渡流区，几何尺寸对高超声速缝隙绕流的影响与连续流区存在不同，主要表现为，当长深比等于4时缝隙内部就出现了双涡结构和剪切层在缝隙底面再附，而连续流区产生类似现象对应的长深比为14。靳旭红等[15]采用DSMC方法研究了70 km,75 km,80 km和90 km等4个飞行高度下稀薄流区高超声速缝隙流动问题。结果表明：上述飞行高度下,外部流动的分离和再附在缝隙内部形成一个充满腔体的单涡结构；稀薄气体效应对缝隙内部流动结构和壁面热流影响明显，随着高度的增加，主涡涡心上移,其形状逐渐变得“扁长”，右上角逐渐变尖，热流越来越集中分布于缝隙下游侧面的顶部区域。

从目前的研究成果来看，上述文献的研究模型主要为不发生形变的矩形结构，并且研究内容主要集中在流场特性方面，而对表面气动参数的研究较少。但是在实际飞行中，高超声速流场中缝隙内表面会受到严重的气动加热，缝隙形状结构尤其是两侧壁面会被强烈的表面热流烧蚀而发生变化。因此，对形变缝隙进行流场结构和气动加热分析显得十分重要。

本文采用直接蒙特卡洛方法进行仿真计算，将缝隙模型简化为壁面可变倾斜角的梯形模型。研究了在稀薄高超声速环境中壁面倾角改变对流场结构和气动热特性分布的影响规律，对飞行器表面优化设计提供进一步的理论帮助。

1 数值方法

DSMC方法的基本思想是：用有限个仿真分子代替真实气体分子，并在计算机中存储仿真分子的位置坐标、速度分量以及内能等信息，并在模拟分子运动、碰撞以及与边界相互作用的过程中不断改变这些信息的具体数值，最后通过统计网格内仿真分子的运动状态实现对真实气体流动问题的模拟，流场的宏观参数可以由统计平均求得。该方法的关键是在时间步长内将分子的运动与碰撞解耦。在时间步长内让所有分子运动一定的距离并考虑在边界的反射，然后计算此时间步长内具有代表性的分子间的碰撞。

本文数值计算工具选择的是美国桑迪亚国家实验室的开源SPARTA程序，并且使用北京并行云科学技术计算中心的工作站来进行数值模拟计算。模拟分子采用可变径软球模型，并考虑到了空气分子的转动能和平动能之间的能量传递过程。分子内能和平动能之间的能量传递采用标准Larsen-Borgnakke模型。另外，本文选择的时间步长为当地自由分子平均碰撞时间的三分之一。模拟分子数在每个网格内最少为10个。

同时，由于采用DSMC方法进行数值计算时，模拟分子数和网格划分引起的计算量非常大，需要开展并行计算。一般并行算法采用区域分解，根据计算的处理器数(或CPU核心数)的多少将计算区域划分为等量的子区域，每个处理器在其分配的子区域内部独立地计算模拟分子的碰撞和迁移，离开子区域的模拟分子把携带的信息传递给对应子区域的处理器。但DSMC方法的一个显著特征是模拟分子在流场中的分布是不断变化的，计算时间依赖于子区域内的分子个数、分子的碰撞次数以及分子与物面的碰撞次数。因为模拟前不可能预测到不同子区域内的分子个数，因此在区域分解时将各子区域的计算负载划分得比较均衡就特别困难。如果简单地将流场均匀划分成若干同等大小的子区域，就有可能造成处理器之间的负载分布不均匀，负载最少的处理器就要花费较长的时间等待负载最大的处理器，造成同步等待的时间显著增加。这种方式并不适合DSMC并行模拟。

本文发展了一套静态随机负载平衡方法用于解决不同处理器之间的计算时间同步问题，该方法基于概率近似原理，将计算区域的全部网格平均分配给指定的所有处理器。由于采用相同的概率随机选取流场网格，按照均分后的数量分配给每个处理器，因此当计算区域的网格数量较多时，每个处理器包含近似相等的物体边界、高密度流动区域和稀薄气体区域的网格数，这样每个处理器的计算负载也非常接近。

2 仿真计算

为了验证SPARTA程序的可行性，首先对二维的平板模型进行了模拟，平板的长度为100 mm，厚度为5 mm，并将模拟计算得到的结果与风洞实验[16]测量得到的结果进行比较。模拟仿真的来流条件设置为风洞的实验条件：来流气体为氮气，自由来流的速度为1504 m/s，平均自由程为1.6 mm，温度为13.32 K，气体分子数密度3.716×1020m-3。

计算域宽度设置为180 mm，水平方向设置360个网格；高度设置为205 mm，垂直方向设置410个网格。每个网格的长宽都是0.5 mm。计算域与平板示意图如图1所示。平板壁面温度为290 K。模拟粒子的仿真比例FNUM设置为4.56×1011，即一个模拟粒子代表4.56×1011个真实分子。时间步长设置为3.102×10-7s。同时，采用自适应结构网格，分子碰撞采用VHS模型，NTC方法进行取样，能量交换采用Larsen-Borgnakke模型，壁面恒温，采用漫反射模型。不考虑气体化学反应。

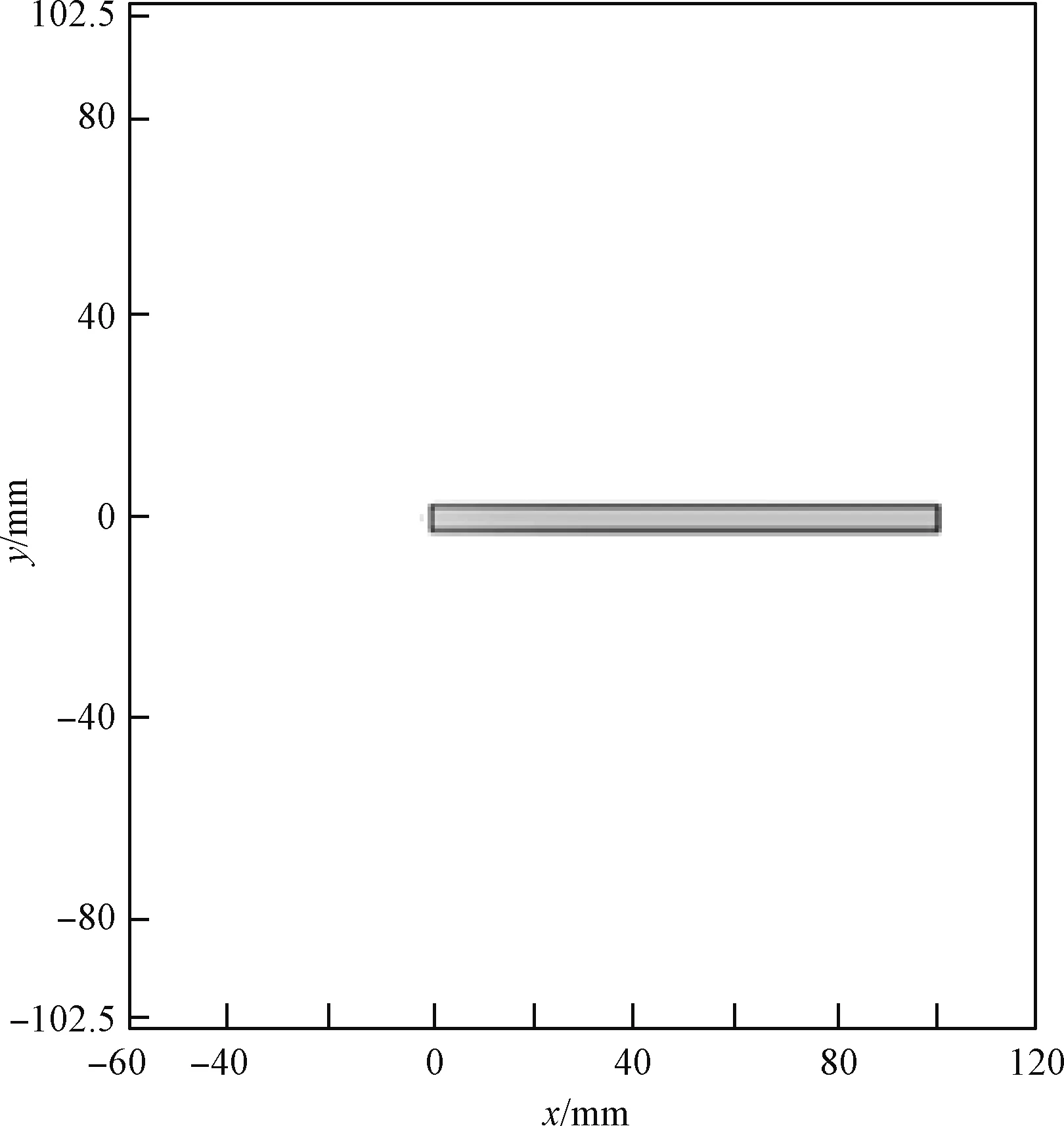
图1 平板测试算例示意图Fig.1 Calculation example of plate tests

平板上平面的压力仿真结果与文献[17]中DAC方法的仿真结果以及风洞实验结果对比，如图2所示。SPARTA方法得到的结果与DAC的结果比较吻合，但是都比实验结果略大，但压力分布的趋势与实验结果大致相同。计算结果表明本文选择的数值方法和计算程序对于这类高超声速流场的计算模拟具有较好的可信度。

图2 仿真结果比较Fig.2 Comparison of simulation results

3 模型和流场参数

3.1 几何定义

临近空间航天器上的表面不连续结构或缝隙远远小于航天器本身的尺寸，因此将航天器表面上的缝隙结构简化为无限长的平面上的矩形缝隙。本文仅对二维情况的缝隙模型进行分析，模型的几何示意图如图3所示。

图3 缝隙模型外形示意图Fig.3 Schematic diagram of the gap model

倾角θ表示前壁面和底面的夹角，倾角θ分别取30°,45°,60°,75°,90°(即矩形缝隙)。定义缝隙的长度为L=9 mm，深度为D=3 mm。缝隙上游的平板长度为3D，下游平板的长度为D。

3.2 来流条件

本文选取的高度为70 km，来流的速度、压强、温度、密度、粒子数密度以及平均自由程均采用美国标准大气(1976) 确定，计算工况如表1所示。气体成分为78%的N2和22%的O2。根据70 km自由来流的平均自由程和缝隙模型的特征尺寸，得到全局克努森数Kn大约为0.3，该缝隙模型的绕流问题属于稀薄流范畴。本文设定缝隙模型的壁面温度Tw为220 K。

表1 自由流条件Table 1 Free stream conditions

4 流场和壁面参数计算公式

4.1 流场特性分析

在本文的研究中主要关注的流场特性参数有流场中的马赫数、压力和温度。DSMC方法中流场的宏观参数是由计算域内每个网格单元中的模拟粒子的参数计算平均得到的。

每个网格单元的质心速度矢量的计算方法为：

(1)

式中：N,mj和cj分别为每个网格单元中粒子的数量、质量和速度矢量。粒子的热运动速度或扰动速度c′定义为

c′≡c-c0

(2)

网格中平动温度TT的计算公式为：

(3)

转动温度TR与网格单元的转动能量εR和转动自由度ζR有关，计算公式为：

(4)

每个网格单元的压力的计算方法为：

(5)

每个网格单元的密度的计算方法为：

(6)

4.2 壁面参数

本文在研究模型的壁面特性时主要关注表面压力系数和表面热流系数。

模型表面的压力pw由每个时间步内入射和反射的粒子在物面上的法向动量之和得出，表达式如下:

(7)

式中：A为物面面积；N为单位时间内在单位面积上与物面碰撞的粒子的个数；v是j粒子在物面法线法向的速度分量；i,r分别表示入射和反射粒子。

压力系数Cp的定义如下：

(8)

热流qw是通过计算碰撞壁面的模拟粒子的净能量通量来计算的，与入射、反射粒子的平动能、转动能和振动能有关，表达式如下：

(9)

(10)

式中：eRj和eVj分别代表粒子的转动能和振动能。

传热系数Ch的定义如下：

(11)

5 流场和壁面参数计算公式

5.1 流场特性分析

5.1.1流线分析

为了清晰地描述缝隙的流动特征，缝隙内回流区的变化是研究的重点。流线图能较好反应出其变化。图4显示了不同侧壁倾角下的流线分布。

图4 缝隙内流线分布图Fig.4 Distribution of streamline traces inside the gaps

从图中可以看出，当θ=90°时，缝隙内部存在连在一起的两个旋涡，此时仍然认为其是一个回流区且填满整个缝隙，上方流线直接跨过缝隙。当θ=75°时，随着倾角的减小，左、右旋涡强度都开始减小，在缝隙上方的外部流体逐渐进入到缝隙内部，缝隙中间的旋涡受到剪切层的挤压作用而往缝隙底部凹陷。在这两种工况下，旋涡仍然是连在一起，是上一种情况的延续，在缝隙内表现为单个旋涡的特性。但两个涡心的距离开始增大。当θ=60°时，在缝隙前、后侧出现了明显分开的两个旋涡，此时剪切层也深入缝隙底部。缝隙右侧旋涡尺寸变化不大，但缝隙的左侧旋涡明显变小。θ=45°时，左侧角落出现非常小的旋涡。对于右侧旋涡区域，它在每种工况下，其姿态和流向长度变化不大。当倾角继续减小，θ=30°时，缝隙的左侧角落几乎被剪切层充满，左旋涡彻底消失，在缝隙左侧壁面上边界层没有流动分离。

综合比较图4，当倾角从90°变化到30°时，缝隙内部的回流区发生了明显的变化，并以60°和 30°作为分界点。当θ≤60°时，缝隙内部出现了两个回流区，且上方的流体能够进入到缝隙的底面；θ≤30°，左侧的旋涡区域完全消失。同时，可以看出，旋涡区域的旋转方向均为顺时针。缝隙右侧的角部涡流与前壁的倾角无关，都保持大致相同的尺寸。可以推断，改变θ的大小对缝隙后壁面区域的影响较小，这会在下文表面参数分析中进行验证。

最后，通过倾斜缝隙后壁面也可以消除右侧的旋涡区域。为此，以30°的角度倾斜缝隙前后壁面，然后使用DSMC方法计算。图5显示了两侧壁面倾角都为30°时的流线分布图。通过与图4中的结果进行比较，发现当后壁面倾角为30°时，缝隙右侧旋涡区域也完全消失。因此，一个重要的结论是，通过以适当的角度倾斜缝隙前后壁面，可以完全消除缝隙内的旋涡区域。

图5 流线分布图Fig.5 Distribution of streamline traces

5.1.2马赫数分析

图6展示了不同前壁倾角θ下缝隙模型的流场马赫数等值线图。

从图中可以看出，当θ=90°时，在缝隙内的大部分区域，其马赫数小于 1，说明在内部回流区的气流速度很小，且由于壁面的黏性作用，在缝隙中间的流体速度大于两侧的流体，缝隙底面中间位置受到的侵蚀最大。当θ减小时，缝隙外剪切层从缝隙中部缓慢地深入，导致最大流速区往前移动，亚声速区被缝隙外剪切层往下压缩到缝隙底部，流场内的整体速度也开始增大。这是由于缝隙前壁面往上游倾斜时，一方面使缝隙具有更宽的开口，一方面让缝隙入口处流体的再附点从缝隙底面移动到缝隙前壁面，外部流动可以更深地作用缝隙内部流动，因此可以看到缝隙内流体速度开始增加。当θ=30°时，亚声速区只存在于缝隙右半区域，缝隙外超声速流场进入缝隙左侧区域。

5.1.3密度云图

图7为不同前壁面倾角时缝隙内部的无量纲密度(当地密度与来流密度之比)等值线图。

从图中可以看出，当θ=90°时，缝隙左侧完全被低密度区占据，其值小于来流密度。又由于气流在后壁面被压缩，缝隙右侧流体密度明显比左侧高很多，密度最高处在缝隙右侧角落。随着倾角θ的减小，流场内的整体密度变化不大，只是由于左侧壁面向前倾斜，缝隙内的低密度区范围也随之往上游延伸。而在缝隙右侧，随着倾角减小，密度只在缝隙右侧角落处略微增大。可以看出前壁面倾角的改变对流场密度的影响较小。

5.1.4压力云图

图8为不同前壁面倾角下缝隙内部的无量纲压力(当地压力与来流压力之比)等值线图。

从图中可以看出，当θ=90°时，在缝隙左侧的压强较低。这是因为当来流经过缝隙的前壁面时，相当于流经一个后向台阶，流场的面积突然增加，自由来流在这里产生流动分离，因此在前壁面顶点处附近出现了局部压强较低的区域。随着前壁倾角的减小，缝隙左侧的低压区域被显著压缩。随着缝隙前壁面的倾斜，缝外高压气流加速流入，压力呈上升趋势。

在缝隙右侧，还可以观察到在后壁面顶点的左上方流场处出现了一个局部高压区域。从流线图中可以看出，这是高速流体撞击在后壁面顶点区域所致。随着θ的减小，该高压区域开始缓慢增大。这也是因为前壁面倾斜，进入缝隙内的流体速度开始增大。其最终会在右侧壁面开始重新被压缩，并且压缩效应随速度的增大而增大，所以，前壁倾角的减小会增大缝隙右侧的压力。又因为稀薄效应，减弱了缝隙内的气流速度对气体压缩的影响，所以，其改变幅度也并不显著。

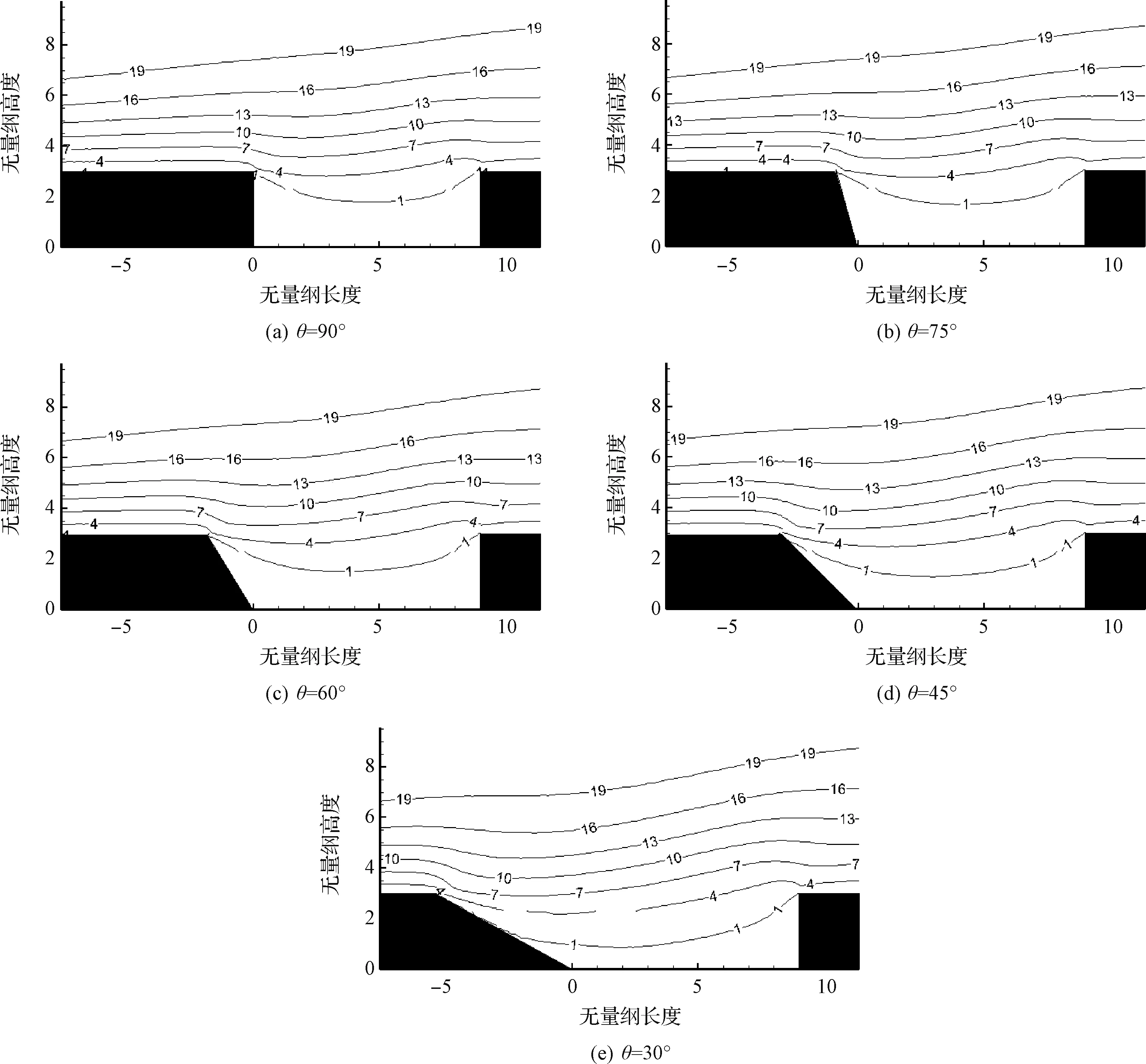
图6 缝隙内马赫数分布Fig.6 Mach number distribution in the gaps

最后，还可以明显发现前壁倾角的改变对流场压强的影响比对流场密度的影响更大。

5.1.5温度云图

图9展示了不同前壁倾角下缝隙内部的无量纲温度(当地温度与来流温度之比)等值线图。

在缝隙左侧，当θ=90°时，低温区占据缝隙左下方区域，也正好是左旋涡区域的范围。当倾角减小时，缝隙前壁面附近的低温区开始减小。高温区开始前移，缝隙内的整体温度也开始有所提高。当θ=30°时，随着左侧旋涡区域消失，缝隙外的高温气流进入缝隙的左侧角落，区域温度明显升高，远大于缝隙右侧角落。同样在缝隙右侧上方，由于压缩作用形成了一个高温区。当倾角减小时，右侧的温度分布基本没有变化，只是缝隙右侧上方形成的高温区范围略微增大。这验证了前壁倾角的改变对缝隙后壁面附近的影响较小。

最后，为了更深入了解其变化，研究其缝隙内部的在稀薄气体流动中的热不平衡效应，对转动温度也进行研究。图10展示了不同前壁倾角下缝隙内部的无量纲转动温度(当地转动温度与来流转动温度之比)等值线图。

综合比较图9，可以看出，当θ=90°时，在缝隙左侧，由于整体温度都较低，平动温度TT与转动温度TR的差距并不明显，该处的热不平衡性较小。而在缝隙右侧，由于气流在后壁面处受到强压缩，该区域的平动温度TT远大于转动温度TR，存在强烈的热不平衡效应。而当倾角减小时，平动温度和转动温度都开始增加，但转动温度增大的幅度更大。当θ=30°时，平动温度和转动温度间的差距小于θ=90°时两者间的差值。这说明倾角减小能减弱缝隙内流场中的热不平衡效应。

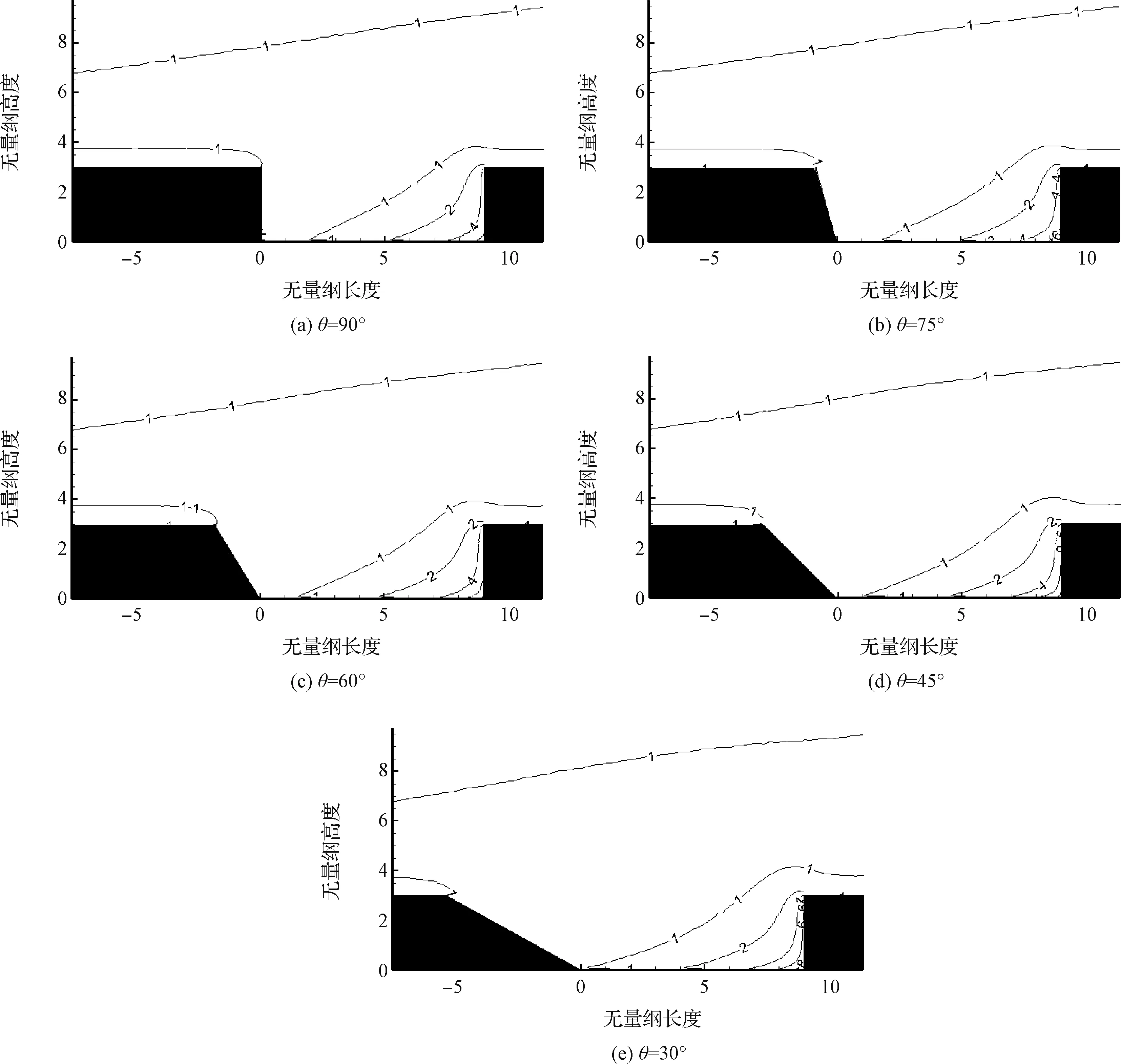
图7 缝隙内密度分布Fig.7 Density ratio distribution in the gaps

5.2 表面参数分析

5.2.1表面热流系数分析

图11分别展示了不同前壁倾角下的缝隙的前壁面、底面、后壁面三个表面上的热流系数分布。

从图中可以看出，在前壁面，当θ=90°时，热流系数从表面顶点往下缓慢增大，在表面中部位置附近达到最大值。之后，热流系数往下再缓慢下降直到表面底端。当θ=75°和 60°时，在表面的上半部分热流分布与θ=90°区别不大。在表面下半部分，热流系数随前壁倾角减小而增大。这是因为，当前壁倾角减小时，其底部附近的流体速度也加快，传热速度也随之增大。当θ继续减小到 45°和 30°时，前壁面上整体热流系数有了大幅提高。热流系数从表面顶点往下单调增大，并在底部位置达到最大值。

在缝隙底面上，对于不同前壁倾角，沿来流方向，表面热流系数都是先增加后减少，因此存在一个热流峰值，峰值对应在底面上的x轴坐标都是约为 0.8，该位置也是缝隙右侧旋涡的起始位置。同时，可以看到，随着前壁倾角的减小，在底面的前半部分，整体热流系数也随之增大。这是因为随着倾角的减小，流体越来越深入缝隙，造成热流系数的整体增加。当倾角越小，增加的速度也越大。在底面的后半部分，不同工况下的热流系数开始趋于定值。

在后壁面上，各工况下的表面热流系数均在顶点处达到最大值，且从顶点沿后壁面向下越来越小。同时，随着倾角的减小，在后壁面的同一位置处，表面热流系数虽然逐渐增大，但幅度很小。这说明改变前壁面倾角θ，并不会对右侧壁面产生较大影响。前壁倾角改变对缝隙内表面的影响主要集中在前壁面以及底面的前半部分。

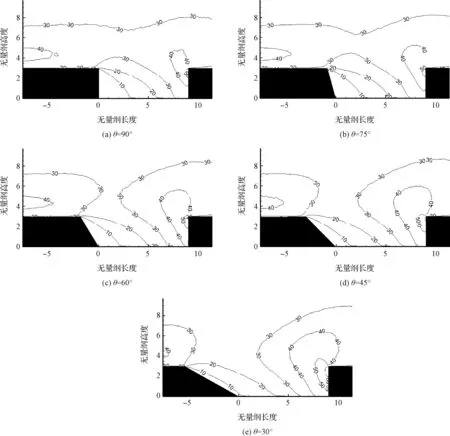
图8 缝隙内压强分布Fig.8 Pressure distribution in the gaps

综合分析三个壁面上的热流系数，热流系数最大的区域是在缝隙的后壁面，这是因为流体在缝隙后壁面产生压缩。同时，随着θ的减小，前壁面和底面的热流系数大幅提高，这会导致前壁面和底面更容易烧蚀，并进一步减小θ值。

5.2.2表面压力系数分析

图12分别展示了不同前壁倾角下的缝隙的前壁面、底面、后壁面三个表面上的压力系数分布。

当倾角θ从 90°减小到 45°时，在前壁面底部的压力系数变化不大，但在底部上方的大部分区域内，压力系数值随着前壁倾角的减小而减小。当θ=30°时，在表面上方部分的压力系数分布曲线和θ=45°时基本相同，但在表面底部，压力系数远大于θ=45°时的分布。这是因为当θ=30°时，缝隙左侧角落旋涡开始彻底消失，流体与表面完全贴合，消除了缝隙角落处旋涡的影响，使得压力系数在底部突然增大。

在缝隙底面上，各工况的表面压力系数都有一个沿来流方向持续增大的趋势，其最大值所对应的位置均在底面最右端取得。同时，底面上整体压力系数随着前壁倾角的减小而增大，不过增大的幅度很小。

在缝隙后壁面上，压力系数的变化规律与热流系数相同。对于不同的工况，表面压力系数在后壁面的顶点处取得最大值，从顶点沿后壁面向下，表面压力系数迅速减小。到表面中部区域时，减速放缓。

图9 缝隙内温度分布Fig.9 Temperature distribution in the gaps

图10 缝隙内转动温度分布Fig.10 Rotational temperature distribution in the gaps

图12 表面压力系数分布Fig.12 Pressure coefficient distribution on the surface

并且在表面的底部区域，表面压力系数基本稳定。同时,在后壁面的同一位置处，倾角越小，对应的表面压力系数越大。这是因为，随着θ减小，缝隙内气流速度增大，对后壁面的压缩效应也随之增强。

6 结 论

本文聚焦高超声速稀薄流航天器表面的缝隙，使用直接模拟蒙特卡洛方法进行数值模拟，对可变壁面倾角的梯形缝隙的流场情况及壁面参数进行分析，结果表明：

1) 侧壁倾斜式变形对缝隙内部流场形成了高温引流和加速导流两种效应。前者可以诱导更多高温流体更深入缝隙内部，流场参数整体有所提高。后者能够加快缝内气体的切向流速，使其更快溢流。两种效应都将促使缝隙底部热流密度升高，而这里是最接近飞行器内部零件的位置，因此壁面倾斜形变将给飞行器缝隙内的热防护带来极为严峻的挑战。

2) 当倾角改变时，缝隙内部的回流区发生了明显的变化，并以60°和30°作为分界点。当θ≤60°时，缝隙内部从一个大旋涡彻底分裂为两个旋涡；当θ≤30°，左侧的旋涡区域完全消失，在前壁面消除了流动分离。同时，通过改变缝隙两侧壁面的角度大小，能完全消除缝隙内的旋涡区域，改善其气动特性。

3) 对于缝隙内的表面而言，前壁面倾角的改变主要影响前壁面和底面前半部分。随着倾角θ的减小，在前壁面，传热系数显著增大，而压强系数减小。而在底面上，传热系数随θ减小而增大，压力系数也小幅增大。在后壁面上，随着θ减小，热流系数和压力系数都有增大，但幅度很小。