固推约束下的火星表面起飞上升制导律设计
2022-12-26郭敏文黄翔宇郭延宁
郭敏文,李 琨,黄翔宇,郭延宁
(1.北京控制工程研究所,北京 100094;2.哈尔滨工业大学航天学院控制科学与工程系,哈尔滨 150001)
0 引 言
目前,中国已经通过嫦娥五号探测器实现了月面采样返回,即将开展小行星就位探测任务,火星采样返回任务也进入方案论证阶段。与地球和月球任务不同的是,火星面临的干扰和不确定性较大,可观测的数据较少,并且存在着通信困难的问题,因此火星采样返回任务困难重重。其中,火星表面上升是火星采样返回中最具挑战性的关键技术,世界上尚无任何先例。由上升段、无动力滑行段和入轨段构成的三段式上升方案是一种经典且有望实用的技术路线,但其面临着初始起飞状态和干扰力矩不确定性大、火星上升器质量特性变化快和气动环境复杂多变等多项挑战。最终入轨精度对于同火星轨道器的交会对接、样本转移等具有重要的影响,因此具有很高的要求。马歇尔太空飞行中心对上升器的推进方案进行了设计与预研,由于固体方案相比于固液混合方案具有更低的起飞质量,系统整体复杂度相对较低并且对工作温度限制不敏感,能够适应较为复杂的环境,所以固体方案更能适应飞行任务的条件与需求[1]。但采用固体发动机也面临独特的困难,一方面是推力大小固定,带来了控制能力有限的问题;另一方面其自身特性要求在燃烧掉所有推进剂前不能提前关机,因此需要针对上升器设计额外的能量管理策略[2]。为了保障上升器能够在固体推进剂约束的条件下定时定点地进入预定轨道,火星表面上升过程的制导控制系统面临着严峻的挑战。
制导策略是上升器安全、高精度地飞行到预定轨道的重要保障。目前关于火星上升制导律的研究相对较少,主要有两种方法:预测校正制导和标称轨迹跟踪制导[3]。预测校正制导主要是通过对最终状态进行预测来分析轨迹,逐步校正,具有较强的灵活性。McCormick等[4]早在1986年就提出了基于预测校正的火星表面上升制导方法,有效处理了各种偏差,但其计算量大、对模型要求较高。洪海超等[5]分别考虑了导弹和着陆器的状态和输入约束,提出了一种新的预测凸规划模型,能够快速高效地解决制导问题。标称轨迹跟踪制导主要任务为跟踪离线优化的标称轨迹,根据实际飞行轨迹与标称轨迹之间的误差设计制导策略。文献[3]总结了火星上升器制导算法的发展和面临的诸多困难,虽然对火星上升器的研究不多,但是可以参考地球、月球表面上升的方案[6]。目前大多数火星探测任务中,出于对可靠性的要求,标称轨迹跟踪制导仍是优先考虑使用的方法。
标称轨迹跟踪制导可主要分为标称轨迹的获取和制导律的设计[7]。标称轨迹的获取即在满足约束条件下最优化预先设定的性能指标来确定飞行轨迹的过程。制导律设计的目的就是通过设计控制加速度或执行机构状态,使上升器能够克服各种干扰与不确定性的影响,对标称轨迹实现跟踪。Ro等[8]使用最优控制理论提出了一种应用在火星大气捕获的阿波罗再入标称轨迹跟踪制导方法。文献[9]将该方法应用到火星上升过程,并通过蒙特卡罗仿真对算法的性能和鲁棒性进行了评价。但是这种方法简化忽略了火星大气的影响,在加入一定约束条件后制导精度会有所下降。文献[10]对该方法进行了改进,增加对滑行段火星大气阻力导致的速度损失的解析预测,使得改进后的制导方法在相对推力角约束下的制导精度得到提升。另外,文献[11]将Lambert制导和通用能量管理方法应用到火星上升器的制导过程中,通过控制上升器偏离最优飞行轨迹,使得上升器具有燃烧多余推进剂的能力,最终完成入轨。
后来为了适应更复杂的情况,逐渐衍生了诸如土星五号火箭的迭代制导和航天飞机的动力显式制导。迭代制导利用简化形式下最优控制解的必要条件来进行自适应制导,它不需要进行大量的地面计算,并且对于外界存在较大干扰的情况具有较好的适应性能[12]。国内的长征二号F火箭首次应用迭代制导方法取得了较高的入轨精度[13]。迭代制导方法是目前应用于液体运载火箭的主要制导方法。吴荣[14]将迭代制导应用于可重复使用火箭返回制导任务中。动力显式制导由Jaggers[15]在基于双线性正切自适应制导的技术上改进发展。McHenry等[6]针对动力显式制导应用于航天方面进行了详细介绍。
综上,目前的火星表面起飞上升制导研究一般关注于某一阶段,尚缺乏全过程整体设计,且未考虑滑行段的制导。但在整个上升过程中,滑行段消耗的时间要远大于其他阶段[16],如果不考虑该段的制导问题,则会造成滑行段结束时距离远拱点误差较大,最终会给入轨段的制导过程增加较大的难度。
因此,本论文基于标称轨迹跟踪制导方法,主要针对上升段、无动力滑行段和入轨段全过程进行制导律设计。在上升段引入了阿波罗式制导策略。考虑到上升器在滑行段的控制需求,在滑行段设计了滑模制导律,通过倾侧角的调整实现上升器所受气动力的改变进而完成对标称轨迹的跟踪,并在最终入轨段采用Lambert制导策略实现精确入轨。
1 问题描述与建模
起飞上升过程可以分为三个阶段,如图1所示。首先,上升器第一级固体发动机点火进入上升段,该阶段目的是使上升器达到一定的高度与速度,固体推进剂消耗完之后,上升段结束,随后进入较长时间的无动力滑行段,当上升器飞到目标轨道远拱点附近时,该阶段结束。最后,第一级分离,第二级点火,在入轨段进行修正后进入目标入轨点。
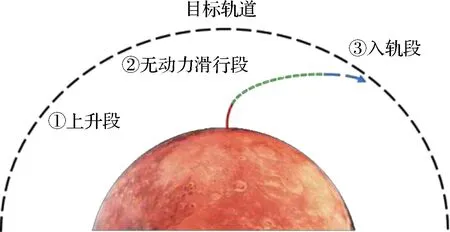
图1 飞行过程Fig.1 Flight process
在上升段由于气动力相对于发动力推力来说很小,为了方便分析在建模时忽略气动力的影响,上升段和入轨段采用Queen[9]提出的动力学模型:
(1)
式中:h为上升器距离火星表面的高度;T为发动机推力;m为上升器的质量;α为攻角;γ为飞行路径角;gm是上升器当前位置的重力加速度;ψ是方位角;v为上升器速度;RM为火星半径。
在无动力滑行段持续的时间较长,发动机不施加推力,如果忽略大气影响则会产生较大的制导偏差,因此借鉴大气进入段的制导方案,通过控制倾侧角来改变上升器所受的气动力,建立无动力滑行段的动力学模型:
(2)
式中:θ是经度;φ是纬度;σ是倾侧角;L和D分别为升力和阻力。升力和阻力的计算方式为:
L=ρv2SCL/(2m)
(3)
D=ρv2SCD/(2m)
(4)
式中:ρ是大气密度;S是参考面积;CL是升力系数;CD是阻力系数。
2 制导律设计
首先利用高斯伪谱法优化得到一条标称轨迹,基于该轨迹设计整个飞行过程的制导律。其中上升段采用阿波罗式制导策略,无动力滑行段和入轨段分别采用滑模轨迹跟踪制导和Lambert制导策略。
2.1 上升段制导
在发动机点火后,由于采用固体推进方案,推力大小为常值,因此只能通过角度的控制来完成该阶段的制导。在该阶段主要通过类攻角和类侧滑角的闭环控制来使上升器跟踪标称轨迹。
(1)类攻角的闭环控制
为了使无动力滑行段结束时的高度与目标轨道远拱点的高度Rt误差最小,定义目标函数:
minJ=ΔR2=(R-Rt)2
(5)
建立相应的哈密顿函数:
H=λhvsinγ+λv(Tcosα/m-gsinγ)+
λγ(Tsinα/(mv)+vcosγ/(RM+h)-gcosγ/v)
(6)
可以得到相关的协态变量方程:
(7)
λγcosγ/(RM+h)-λγgcosγ/v2
(8)
λγvsinγ/(RM+h)-λγgsinγ/v
(9)
为了得到上升段的协态变量λ=[λh;λv;λγ],以上升段协态变量的终端值作为条件,反向积分到上升段初始时刻,由此就可以建立上升段的协态变量表。
将上升器的速度v作为独立变量可以从协态变量表中获取当前速度下对应的协态变量,然后通过式(10)计算得到类攻角的修正量。将该修正量与当前速度对应标称轨迹的控制量相加即可得到类攻角的控制量输入,关于类攻角控制的结构如图2所示。
Δα=-λTΔX/λα
(10)

图2 类攻角的闭环控制Fig.2 Closed-loop control of the angle of attack
(2)类侧滑角的闭环控制
类侧滑角的控制主要是根据当前方位角和飞行路径角进行计算,结构图如图3所示。
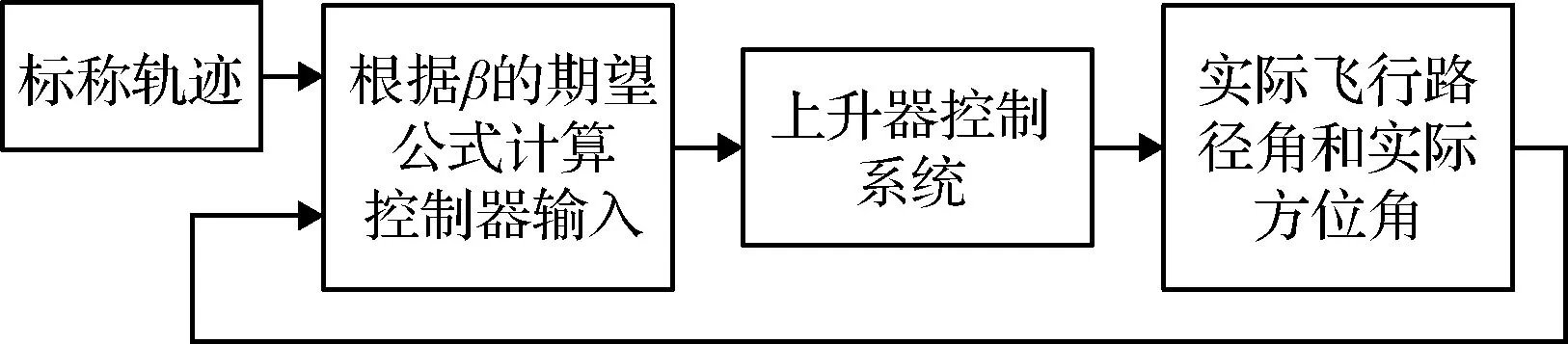
图3 类侧滑角的闭环控制Fig.3 Closed-loop control of the sideslip angle
首先获得当前飞行参数,然后以速度为独立变量在标称轨迹中获得目标方位角,再通过式(11)计算出类侧滑角控制输入量,以实现目标方位角的跟踪过程。
β=arcsin[mv(ψdes-ψact)cosγact/(ΔtT)]
(11)
式中:ψdes是目标方位角;ψact是实际方位角;Δt是制导控制周期。
2.2 无动力滑行段制导
在多数无动力滑行段的飞行方案中,往往认为该阶段飞行时不受大气的影响,而由轨迹优化的结果可知在该阶段时有一段时间处在火星大气层内,在没有施加推力的情况下,如果忽略气动力的影响,可能会产生较大的入轨偏差。
即使阿波罗式火星表面上升段制导方案能够在上升段较好地跟踪标称轨迹,但是在第一级耗尽点产生偏差后,滑行段由于没有施加控制进行修正,会引起偏差的进一步扩大,造成最终入轨精度较低的问题。
经过分析,无动力滑行段的飞行过程与大气进入段相似,因此可以借鉴大气进入段的控制方案,考虑到上升器在滑行段的控制需求,在滑行段设计了滑模制导律,通过倾侧角的调整改变上升器所受的气动力,实现对标称轨迹的跟踪。
首先构建辅助变量,并且令r=h+RM:
(12)
可以得到
(13)
式中:d1和d2代表着参数不确定性和外界扰动,并且假设它们的变化率是有界的。

对滑模面进行求导可以得到
g(x)u+Xd+d1+kd2
(14)
(15)
d1和d2不能被精确测量,所以需要设计观测器对d1和d2进行估计。
下面对d1进行估计,选取滑模面
(16)
观测器可以设置为
(17)

为了尽快收敛到滑模面,提高控制器的性能,选择趋近律
(18)
最终,可以得到制导律如下
u=g-1(x)(-f(x)-Xd-k1sgn(s0)-
(19)
(20)
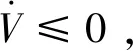
σ=arccos(u)
(21)
改变倾侧角的符号不会影响纵向运动的精度,而能起到改变横向运动的效果。因此,通过设计倾侧角的符号逻辑,实现控制上升器横向运动的效果。
将航向角误差阈值作为倾侧角符号切换的判据,将阈值设计为上升器速度的一次函数:
s3=η1v+η2
(22)
当航向角误差到达阈值边界时,倾侧角改变符号,即
sgn(σ)=-sgn(eψ)
(23)
2.3 入轨段制导
在整个飞行过程中,滑行段的时间较长,而两级上升器的燃烧时间都很短,因此可以将其看为两次点火的Lambert转移。在飞向目标的过程中,滑行段占用的时间越多,Lambert制导的效果就越好。另外,Lambert制导策略可以保证在达到目标位置时燃料消耗完毕,能够满足能量管理的需求。Lambert制导的思路是:从无动力滑行段结束时开始,计算在固定燃烧时间(第二级的燃烧时间)下上升器从当前位置转移到目标位置所需要的速度vgo,根据当前速度v0和计算出的当前所需速度vgo可以得到在该状态下所需的速度增量如下式所示:
Δv=vgo-v0
(24)
(25)
根据式(25)可以将该速度增量转化为目前所施加的控制量u,即完成了当前时刻的控制量的求算,在入轨段不断循环该过程即可实现入轨段的Lambert制导,具体流程如图4所示。
由于发动力推力的大小是不变的,利用Lambert制导时的一个缺陷就在于,计算得到的速度增量转换为推力方向产生的控制效果并不能够瞬时产生相应的速度增量作用于系统,因此每一次计算都会产生一定的偏差,为了消除偏差对最终入轨精度的影响,结合轨迹优化得到的控制量对最终的控制u进行加权处理如下:
u=w1·uLam+w2·unor
(26)
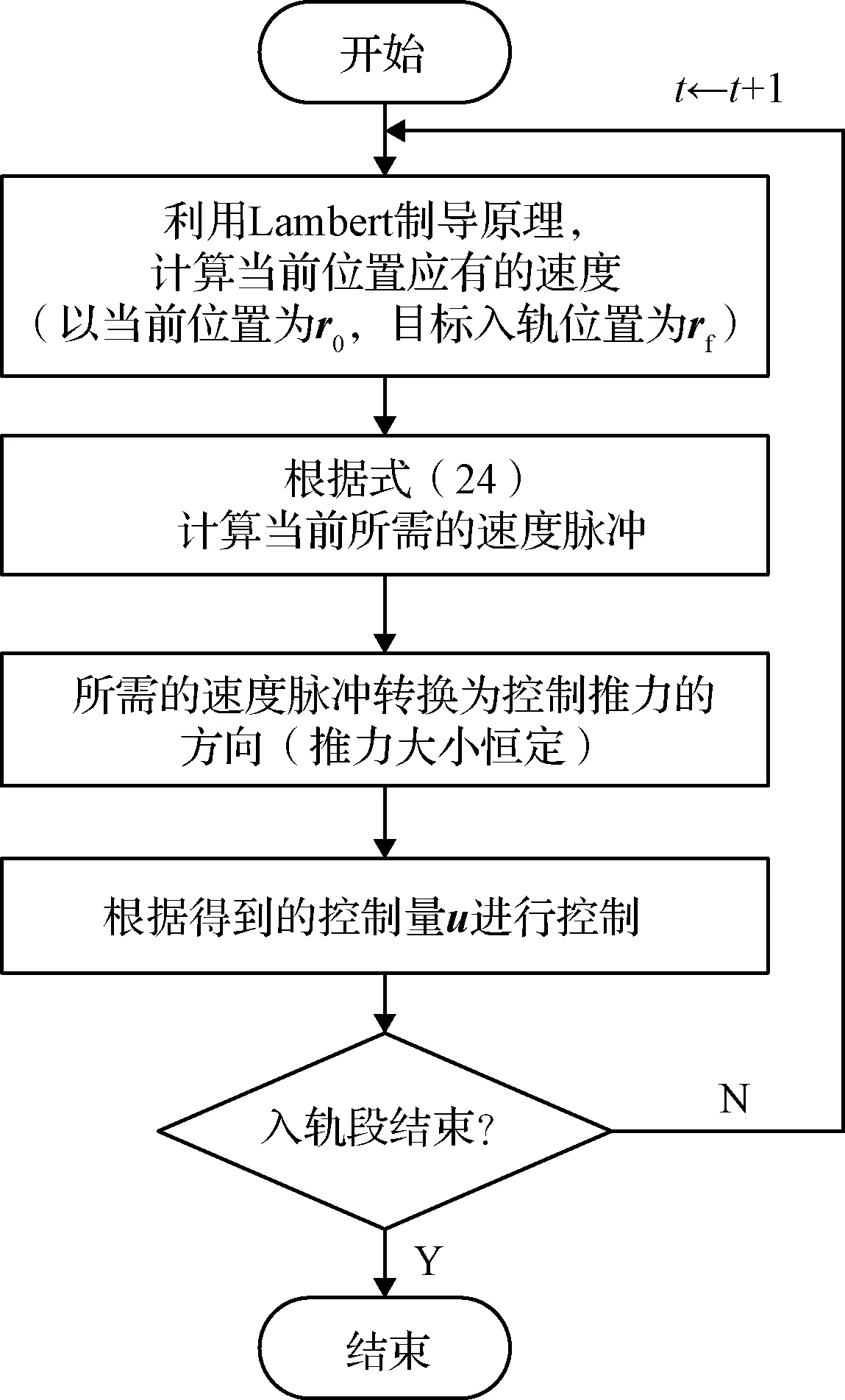
图4 Lambert制导流程Fig.4 Lambert guidance process
式中:w1和w2分别为Lambert制导策略计算得到的控制量uLam和标称控制量unor的权重。该处理的目的是使最终控制量的成分中既包含Lambert制导又包含参考轨迹,并且由于控制饱和问题的存在,因此对权重要求并不高,主要根据前两段的跟踪效果进行选择。这样既避免了采用开环制导带来的弊端,又能结合参考控制量对Lambert制导算法带来的问题进行补偿,进一步提高了入轨精度。
3 仿真校验
两级固体上升器每一级的参数配置如下:

表1 MAV参数表[10]Table 1 MAV parameters[10]
根据以上参数采用高斯伪谱法进行轨迹优化作为标称轨迹,对上升器制导全过程进行数值仿真,其中仿真案例为从赤道上0 km的高度发射上升器飞行到高度500 km、轨道倾角为45°的圆形环火轨道,在入轨段制导时控制权重取值为w1=0.6和w2=0.4,可以得到以下结果:
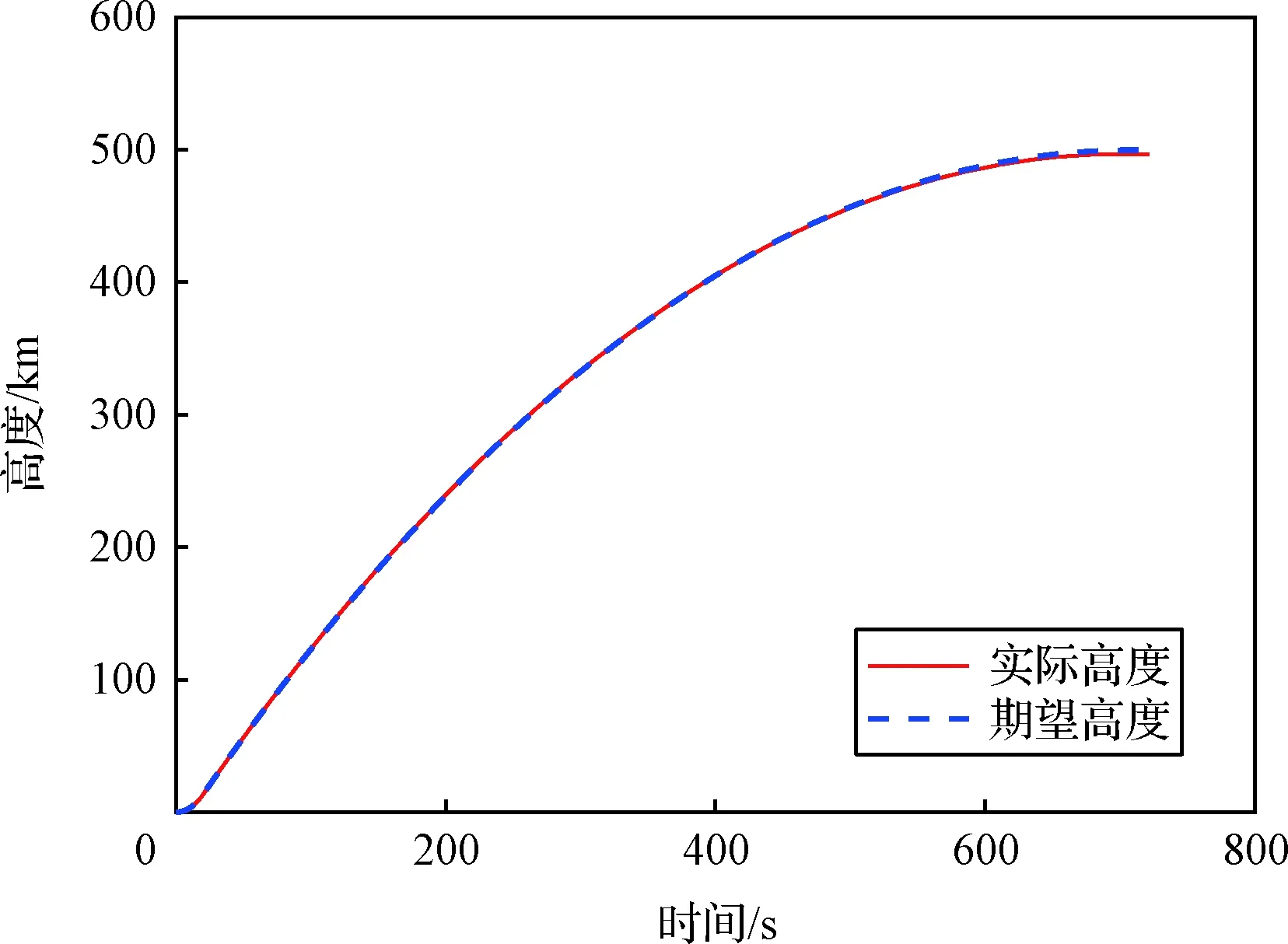
图5 上升高度Fig.5 Flight altitude

图6 飞行速度Fig.6 Flight speed
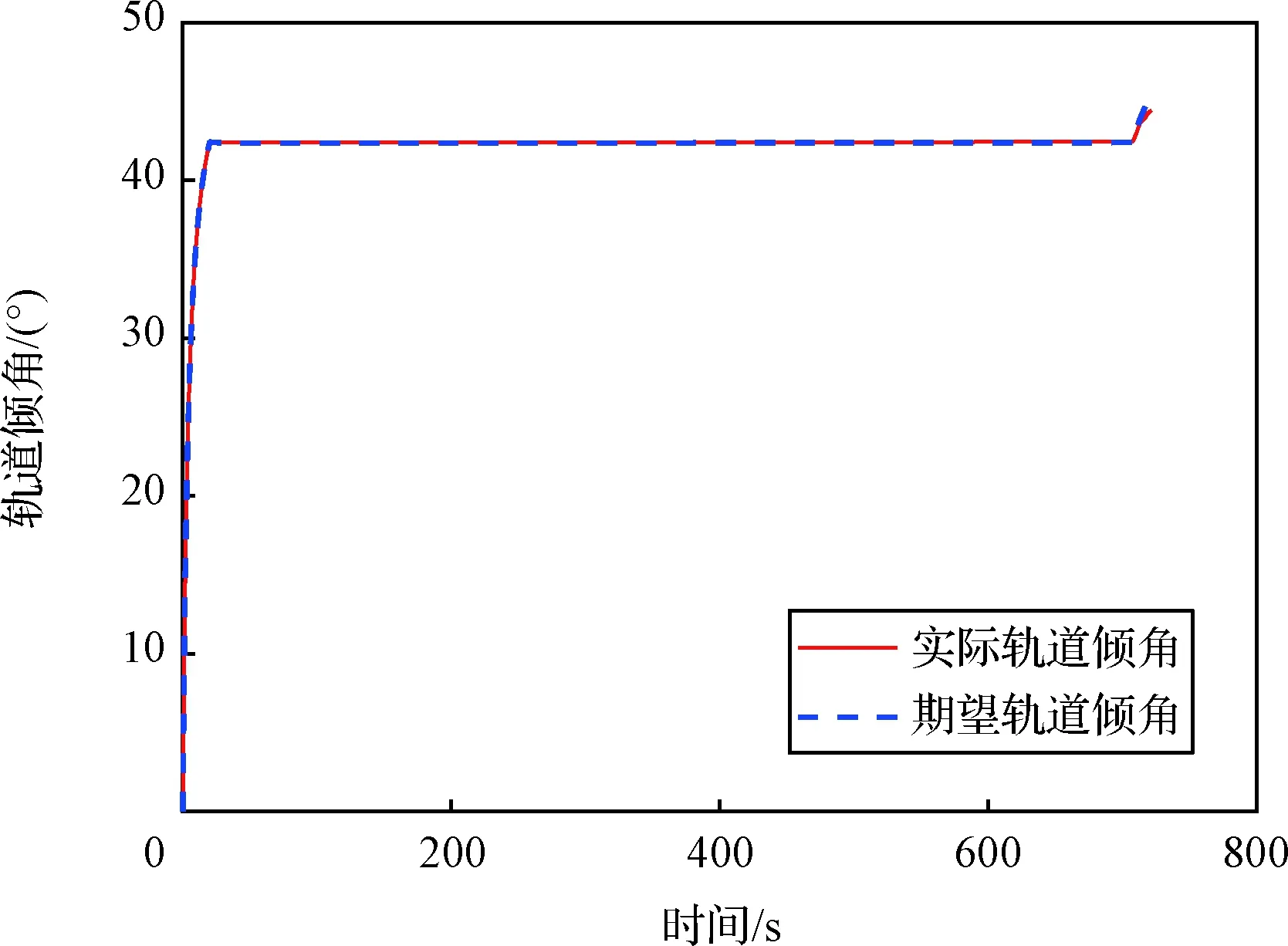
图7 轨道倾角Fig.7 Orbital inclination

图8 轨道偏心率Fig.8 Orbital eccentricity
由图5~图8可以看出,所设计的全过程制导策略能够对标称轨迹实现较好的跟踪,并且在入轨点处的轨道倾角和偏心率都能够控制在期望值附近。
为了进一步验证该方法的鲁棒性,在如表2所示的随机误差范围下进行500次蒙特卡洛仿真,可以得到以下仿真结果。
根据以上仿真结果可以看出500次实验的制导效果,在考虑初始偏差和参数不确定性时,该制导策略具有一定的鲁棒性。在上升段制导结束存在误差的情况下,无动力滑行段通过对气动力的调控减小了误差带来的影响,最后完成入轨段制导,实现了高精度的入轨。

表2 随机误差范围Table 2 Random error margins
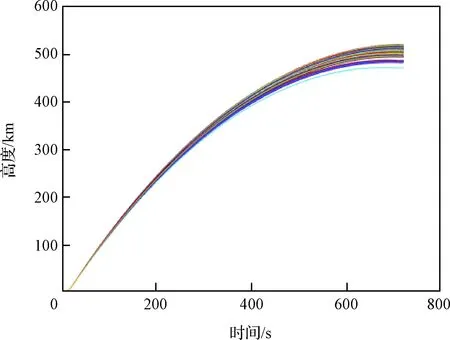
图9 上升高度Fig.9 Flight altitude

图10 飞行速度Fig.10 Flight speed

图11 轨道倾角误差Fig.11 Orbital inclination errors

图12 轨道偏心率误差Fig.12 Orbital eccentricity errors
4 结 论
本文研究了固推约束下三段式火星表面起飞上升全过程制导律的设计问题。首先,分别针对上升过程中的三个阶段进行建模分析,在上升段采用阿波罗式上升制导方案,而针对于滑行段设计了一种滑模轨迹跟踪制导方法,通过调整倾侧角来控制飞行器的运动轨迹,使得对标称轨迹跟踪的精度大大提升,最后在入轨段采用Lambert制导策略进一步缩小入轨误差,通过实际仿真验证了所设计制导方法的可靠性。
