三体随动跟踪式重力卫星姿态与无拖曳控制方法
2022-12-26郑多锦赵艳彬谢进进
廖 鹤,郑多锦,赵艳彬,祝 竺,谢进进
(1.南京航空航天大学航天学院,南京 210016;2.上海卫星工程研究所研发中心,上海 201109)
0 引 言
空间科学作为前沿性、创新性、引领性、挑战性极强的科技领域,在国家创新驱动发展战略进程中发挥着至关重要的作用。近年来,随着暗物质探测卫星“悟空”、无拖曳技术试验卫星“太极一号”、“天琴一号”和太阳探测科学技术试验卫星“羲和号”等空间科学卫星相继研制与发射,极大地提升了我国空间科学在国际上的影响力[1-2]。
重力卫星作为空间科学领域的重要组成部分,通过质量块以及测距系统实现地球全局重力场的反演。当前,国际上采用高低卫卫跟踪模式(Satellite-to-satellite tracking in the high-low model,SST-hl)的CHAMP(Challenging minisatellite payload)、采用微波测距低低卫卫跟踪模式(Satellite-to-satellite tracking in the low-low model,SST-ll)的GRACE(Gravity recovery and climate experiment)和采用重力梯度测量模式(Satellite gravity gradiometry,SGG)的GOCE(Gravity field and steady-state ocean circulation explorer)相继发射升空,可实现200阶静态地球全局重力场的反演能力[3]。
为了进一步提升时变地球重力场的反演性能,NASA正在发展下一代激光测距低低卫卫跟踪重力卫星,并发射了技术试验卫星GRACE Follow-on,有效验证了星间高精度测距等载荷关键技术,欧洲航天局(ESA)也提出了下一代重力卫星任务NGGM(Next generation satellite gravimetry mission)计划。相比微波测距低低卫卫跟踪重力卫星,下一代激光测距低低卫卫跟踪重力卫星平台的关键技术指标要求更高[4-6],如表1所示:

表1 低低卫卫跟踪重力卫星平台关键技术指标Table 1 Key technical indicators of SST-ll satellite platform
根据NASA和ESA公布的设计方法,下一代激光测距低低卫卫跟踪重力卫星采用的均是以卫星本体为基准的“质量块—卫星本体”两体架构设计,并采用微推进系统实现姿态与无拖曳控制。这类卫星控制的概念最早可追溯至20世纪60年代[7-8]。在算法层面,Fichter等[9]提出了一种H∞回路成型姿态与无拖曳控制器;曹喜滨等[10]建立了基于干扰观测的无阻力卫星动力学模型,以线性矩阵不等式形式给出求解混合H2/H∞控制器的条件;Wu等[11]基于定量反馈理论提出了一种姿态与无拖曳控制器;张锦绣等[12]提出了无速度测量的无拖曳卫星自适应控制方法;苟兴宇等[2]和李洪银等[13]研究了天琴的无拖曳控制方法;Dang等[14]研究了一种内编队架构下的控制问题;Zhang等[15]针对无拖曳卫星设计了一种线性自抗扰控制器;杨飞等[16]基于饱和约束测量扩张状态滤波提出了一种无拖曳卫星位姿自抗扰控制器。Canuto等[17]基于扩张观测干扰估计与补偿控制理论,提出了一种嵌入式模型控制,Hu等[18]也基于嵌入模型控制设计了“太极一号”的无拖曳控制器,从在轨应用来看,该方法由于具备较好的工程适用性,并可将控制器的设计与地球重力场恢复频带相匹配,当前在轨应用最为广泛。
然而,由于微推进系统的喷气延迟会导致动态误差,尽管基于扩张观测的干扰估计与补偿控制算法可有效保证高精度线无拖曳水平,但低带宽的微推进系统会限制姿态控制性能提升。与此同时,重力卫星需要保证质量块质心与卫星本体质心之间的偏移尽量重合不变,否则地球重力场反演就会受到耦合的科氏加速度及其基线偏差影响。虽然考虑了在轨质心偏移校准和调整技术,但任务期间由于微推进系统工质消耗会引起卫星本体质心的波动[19]。
针对上述问题,根据作者团队近年来在非接触卫星平台方面的研究基础,探讨了将其应用至地球重力场测量中,在质量块跟踪非接触卫星平台模式下提升姿态与无拖曳控制性能的可行性[20]。但该模式主要以静电悬浮加速度计为无拖曳控制环路的输出反馈,仍然需要采用在轨质心偏移校准和调整技术。因而,本文进一步提出了一种以质量块为参考基准的“质量块—载荷舱—平台舱”三体随动跟踪式重力卫星架构,采用高精度非接触洛伦兹力执行器将整个重力卫星分为“质量块—载荷舱”和“载荷舱—平台舱”两个随动跟踪控制回路。其中,“质量块—载荷舱”回路采用非接触洛伦兹力执行器代替微推进系统实现姿态与无拖曳控制,有效降低质心波动与执行机构带来的动力学特性不确定影响,并且带来应用上的优势,使得质量块以更高精度追踪引力线;同时构建了一种基于带宽参数化自适应补偿的复合自抗扰控制方法,有效提升频域控制性能。“载荷舱—平台舱”回路类似传统重力卫星控制方法,采用微推进系统实现平台舱对载荷舱的跟踪控制,在非接触洛伦兹力执行器线性域运动范围内避免与载荷舱的碰撞即可。
1 总体设计方法
1.1 随动跟踪式总体架构设计
“质量块—载荷舱—平台舱”三体随动跟踪式重力卫星架构如图1所示。

图1 三体随动跟踪式重力卫星架构Fig.1 Architecture of the three-body close-tracking gravity satellite
该架构在传统重力卫星设计的基础上引入非接触洛伦兹力执行器[21-23],在空间结构上将卫星分离为无直接物理接触的载荷舱和平台舱两部分,质量块则置于刚性载荷舱真空腔内。其中,有效载荷(星敏感器、激光测距系统、导航接收机等)置于载荷舱,存在动力学干扰的单机部件(推进器、燃料储箱等)放置于平台舱,实现“动静隔离”设计,为质量块提供超静工作环境;非接触洛伦兹力执行器替代可变微推进系统,通过其控制电流的解耦分配实现载荷舱的主动超高精度姿态与无拖曳控制,并采用较低精度微推进系统实现平台舱协同载荷舱从动避碰控制,达到“主从协同”控制效果,从而保证载荷舱具备超高精度姿态和无拖曳水平。
其中,非接触洛伦兹力执行器是一种高精度力控线性执行机构,相比微推进系统,其在精度一致的情况下具有响应快、动态范围大的优点。当前,非接触洛伦兹力执行器已在国家科技重大专项制程光刻机项目中实现了线性域运动范围内的纳米级精密驱动控制,达到国外重力卫星微推进系统的指标水平[24]。因此,这也意味着采用非接触洛伦兹力执行器代替微推进系统实现超高精度姿态与无拖曳控制具备可行性。
最后,随着无线能源传输与无线数据传输技术近年来的成熟,可有效避免载荷舱与平台舱间电缆连接带来的振动传递问题[25],也可通过给载荷舱蓄电池充满电再卫星整体工作的在轨飞行模式设计降低无线传输的干扰影响。因此,这也意味着这种总体架构具备工程应用可行性。
1.2 低低跟踪编队模式
当前下一代低低跟踪重力测量卫星模式采用同轨道双星编队,基于姿态与无拖曳控制保障,通过加速度计的非保守力测量信息和星间高精度激光测距信息,实现地球重力场反演。
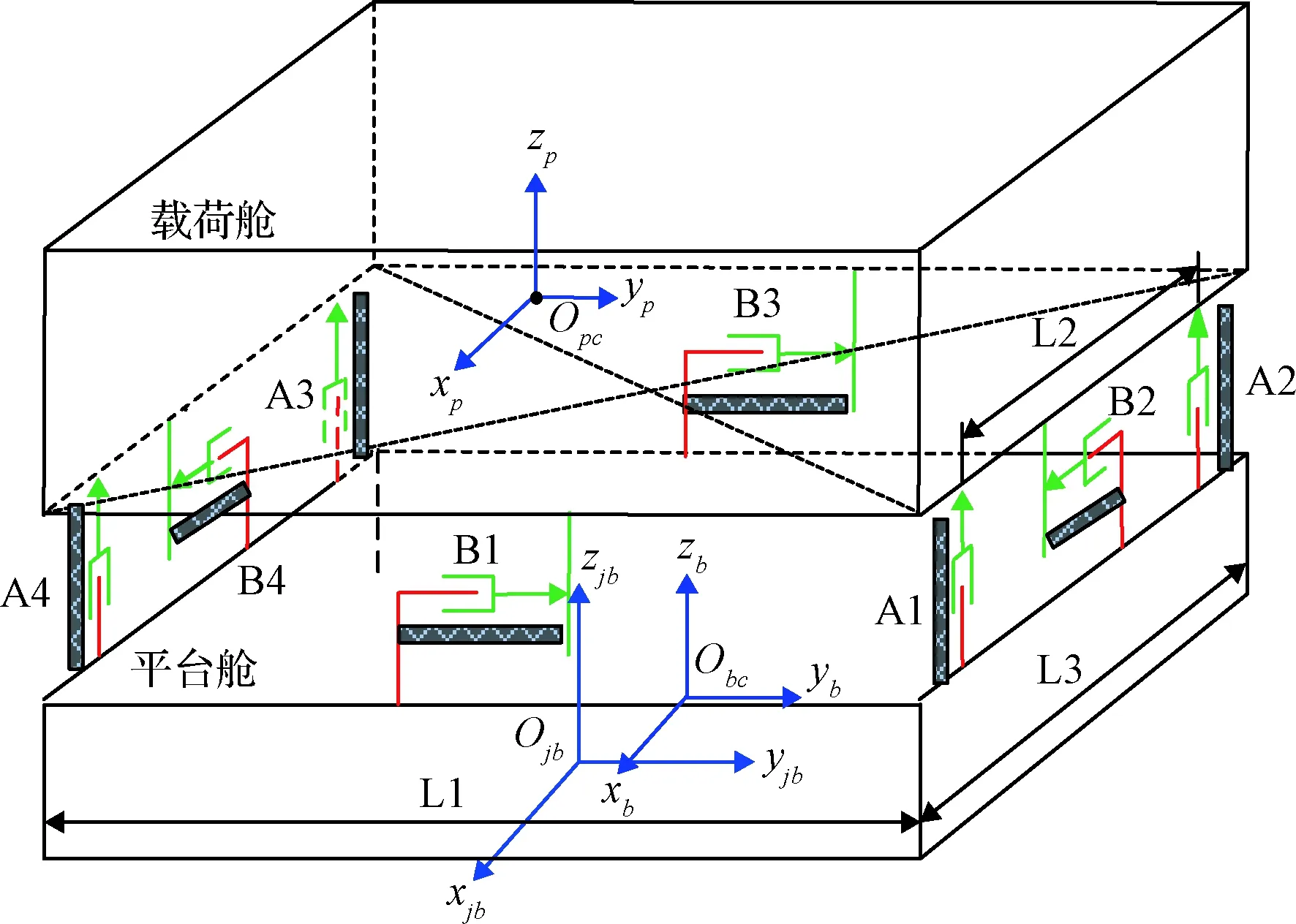
与传统模式不同,文中架构以质量块为参考基准,载荷舱跟踪质量块进行姿态与无拖曳控制,平台舱跟踪载荷舱进行避碰控制,使得质量块高精度追踪引力线。相比传统模式,该设计方法可有效降低质心波动引起的非保守力误差和基线误差的影响,直接通过星间高精度测距信息便可实现重力场的反演。文中低低跟踪编队模式的飞行及其参考坐标系如图2所示。

图2 低低跟踪编队及其参考坐标系Fig.2 SST-ll formation and its coordinate frame
在重力场测量任务模式下,为了保证两星之间的激光测距精确对准,定义姿态与无拖曳控制系统的轨道参考坐标系为FLOF(Formation local orbit frame)坐标系,其原点为SCA和SCB两卫星连线中点,Xf轴为SCA和SCB两卫星连线方向,Yf轴垂直于两星与地心三点构成的平面,Zf轴方向为从地心指向两卫星连线中点[26]。实际上,轨道参考坐标系FLOF系相比于单星时的轨道参考坐标系O系,绕Y轴旋转了角度θfo。
1.3 控制策略设计
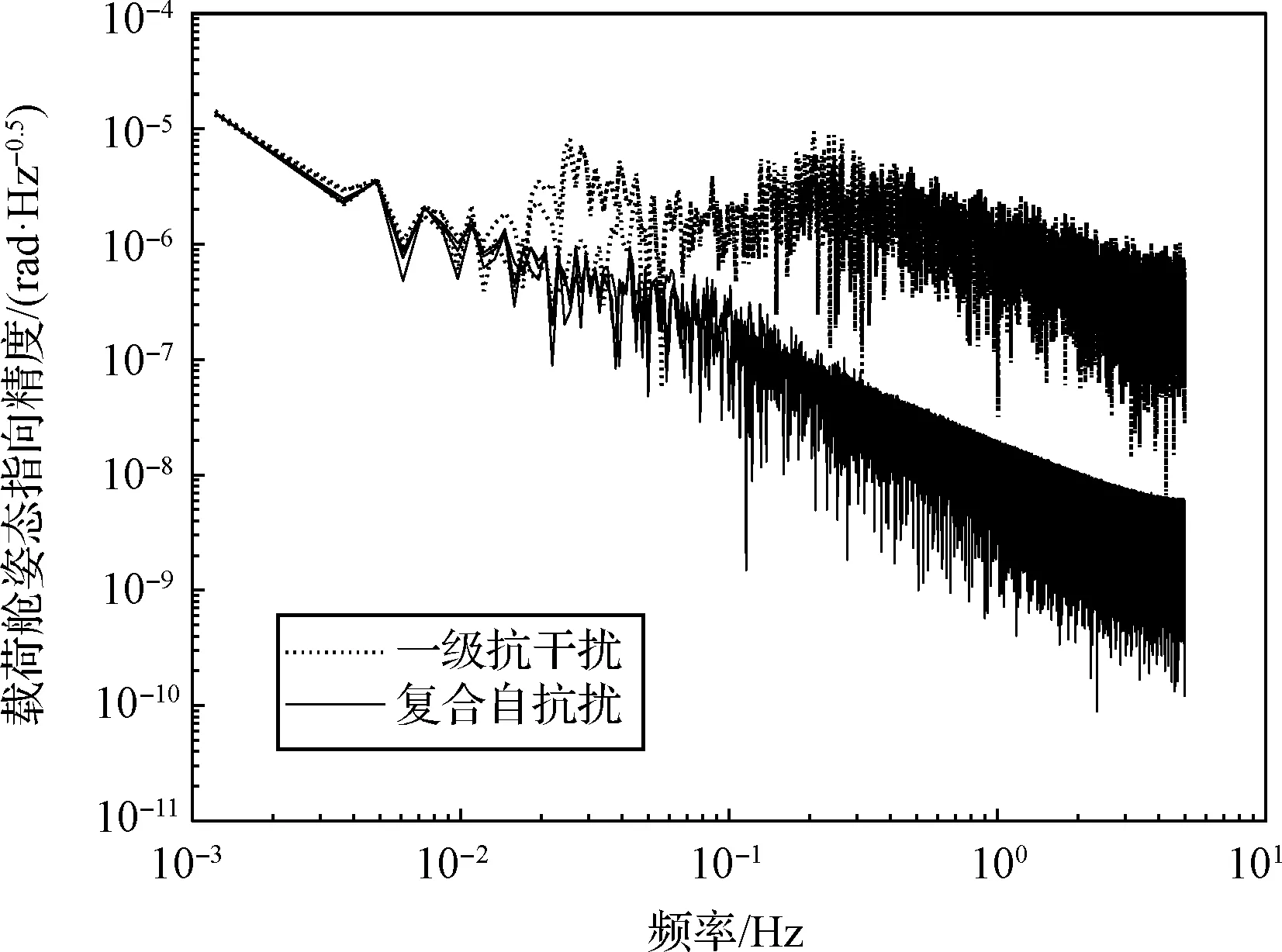
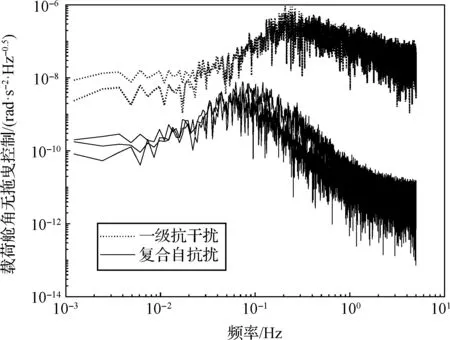
首先,为满足地球重力场恢复的需求,控制系统频带定义如下:低频段ζ0={f 图3 三体随动跟踪式重力卫星控制系统Fig.3 Control system of the three-body close-tracking gravity satellite 为实现载荷舱的高精度姿态与无拖曳控制,“质量块—载荷舱”回路的测量敏感器采用重力卫星中已成熟应用的电容式传感器。电容式传感器是基于桥式测量、面积变化测量、电荷转移测量等多种技术的基础上发展起来的。根据文献[28]中的研究成果,电容式传感器的噪声功率谱密度在中频段ζ1内优于10 nm·Hz-0.5。与此同时,非接触洛伦兹力执行器作为执行机构,在其线性域运动范围内可以提供超精密的力控性能。根据团队近年来的研究基础,非接触洛伦兹力执行器的噪声功率谱密度在中频段ζ1内优于2 μN·Hz-0.5,该指标已达到重力卫星配置微推进系统的指标水平[20]。 为确保非接触洛伦兹力执行器提供的六自由度控制输入,设计了如图4所示的8杆非接触洛伦兹力执行器对称构型。该构型在保证控制系统可靠性和冗余性的前提下,为控制算法的设计带来了两个优点。第一,采用最小范数解耦方法可以获得每个非接触洛伦兹力执行器的驱动控制电流,该方法已被证明是全局最优[20];第二,激光干涉相对位置传感器可以与非接触洛伦兹力执行器同时安装,为“载荷舱—平台舱”随动跟踪控制回路提供量测信息。 图4 8杆非接触洛伦兹力执行器对称构型Fig.4 Symmetrical configuration with 8 non-contact Lorentz actuators 最后,“载荷舱—平台舱”随动跟踪控制回路的主要目的是为了给载荷舱提供无线电源和通信保障,不需要“质量块—载荷舱”随动跟踪控制回路那样严格,因此,只需要采用较低精度微推进系统在非接触洛伦兹力执行器的线性域运动范围内实现平台舱跟踪载荷舱的避碰控制即可。 “质量块—载荷舱”回路动力学模型选择J2000.0地心赤道惯性坐标系为惯性参考系,质量块和载荷舱本体坐标系与各自的质量分布重合,符合笛卡尔右手准则。由于真空腔内质量块的理想轨道运动为跟踪引力线,但考虑到真空腔的设计会产生残余加速度,并且存在质量块与载荷舱之间的耦合干扰加速度,因此,根据牛顿定律,质量块的轨道运动方程可以写为: (1) 式中:rti和gti分别为质量块在J2000.0地心赤道惯性坐标系下的位置和引力加速度;Cti为质量块本体坐标系到J2000.0地心赤道惯性坐标系的姿态转换矩阵;fres为真空腔内的残余加速度,主要包含辐射效应、残余气阻加速度等;fcpt为质量块与载荷舱之间的耦合干扰加速度,主要包含自引力与导电金丝引起的耦合干扰加速度。 与上式相似,载荷舱在J2000.0地心赤道惯性坐标系下的运动可描述为: (2) 式中:rpi和gpi分别为载荷舱在J2000.0地心赤道惯性坐标系下的位置和引力加速度;fenp为载荷舱的环境干扰加速度;fconp为非接触洛伦兹力执行器的控制加速度;mt和mp分别表示质量块和载荷舱的质量;Cpi为载荷舱本体坐标系到J2000.0地心赤道惯性坐标系的姿态转换矩阵;Cpt表示载荷舱本体坐标系到质量块本体坐标系的姿态转换矩阵。 定义质量块的质心和载荷舱的质心在J2000.0地心赤道惯性坐标系下的相对位置为ρi,则可得到: ρi=rpi-rti (3) 对式(3)求两次微分: (4) 将式(1)和式(2)代入式(4)得: (5) 式中:fggi=gpi-gti为J2000.0地心赤道惯性坐标系下的重力梯度加速度。 则J2000.0地心赤道惯性坐标系下的相对位置ρi与载荷舱本体坐标系下的相对位置ρp之间的时间导数关系可以写成: (6) (7) 式中:ωpi为载荷舱本体坐标系相对于J2000.0地心赤道惯性坐标系的角速度。 将式(5)代入式(7),可得到载荷舱本体坐标系下“质量块—载荷舱”回路平动跟踪动力学模型为: (8) (9) 式中:fggp为载荷舱本体坐标系下的重力梯度加速度;μ为地球引力常数;[c1c2c3]T为载荷舱质心与地心单位矢量在载荷舱本体坐标系中的投影。 卫星姿态控制的任务是将质量块本体坐标系与轨道参考坐标系FLOF系三轴对齐。定义三体随动跟踪式重力卫星SCA和SCB轨道高度为H,星间距离为L,则双星编队轨道参考坐标系FLOF系相对单星时轨道参考坐标系O系绕Y轴旋转角θfo为: (10) 可得FLOF系到O系的姿态转换矩阵Cfo为: (11) 定义质量块本体坐标系相对于惯性系的角速度为ωti,质量块相对于惯性系的运动可以拆分成质量块相对于轨道参考坐标系FLOF系的运动和FLOF系相对于惯性系运动两部分,即: ωti=ωtf+ωfi (12) 式中:ωtf为质量块本体坐标系相对于轨道参考坐标系FLOF系的角速度;ωfi为轨道参考坐标系FLOF系相对于惯性系的角速度。 将上式投影至质量块本体坐标系下,可得: (13) 式中:Ctf表示质量块本体系到轨道参考坐标系FLOF系的姿态转换矩阵;Cto表示质量块本体系到轨道参考坐标系O系的姿态转换矩阵。 将式(13)两边在质量块本体系下求导可得: (14) 质量块相对惯性系的姿态动力学方程为: (15) 式中:Jt为质量块的惯量矩阵;Tct为电容电极施加的控制力矩;Tnt为作用在质量块上的残余力矩;Tcpt为质量块与载荷舱之间的耦合力矩。 将式(14)代入式(15)可得到质量块相对轨道参考坐标系FLOF系的姿态动力学方程为: (16) 与式(15)相似,载荷舱相对惯性系的姿态动力学方程为: (17) 式中:Jp为载荷舱的惯量矩阵;Tcp为非接触洛伦兹力执行器施加的控制力矩;Tnp为作用在载荷舱上的环境干扰力矩。 将载荷舱本体坐标系相对于质量块本体坐标系的角速度定义为ωpt,可得如下关系: (18) 在J2000.0地心赤道惯性坐标系中对式(18)求导,则载荷舱本体坐标系相对于质量块本体坐标系的角加速度为: (19) 将式(15)和式(17)代入式(19),可得到载荷舱本体坐标系下的“质量块—载荷舱”回路转动跟踪动力学模型为: (20) 式中:θpt表示载荷舱本体坐标系相对于质量块本体坐标系的欧拉角。 为了建立三体随动跟踪式重力卫星“载荷舱—平台舱”回路动力学模型,平台舱本体坐标系与其质量特性分布重合,符合笛卡尔右手准则。 与上节所示“质量块—载荷舱”回路平动跟踪动力学模型相似,定义平台舱本体坐标系下平台舱和载荷舱的相对位置为ρs,则平台舱本体坐标系下“载荷舱—平台舱”回路平动跟踪动力学模型为: (21) 式中:fggs为平台舱本体坐标系下的重力梯度加速度;fens为平台舱环境干扰加速度;fcons为微推进系统的平动控制加速度;Csp表示平台舱本体坐标系到载荷舱本体坐标系的姿态转换矩阵;ωsi表示平台舱本体坐标系相对J2000.0地心赤道惯性坐标系的角速度。 与上一节所示的“质量块—载荷舱”回路转动跟踪动力学模型相似,定义平台舱本体坐标系相对于载荷舱本体坐标系的欧拉角为θsp,平台舱本体坐标系下“载荷舱—平台舱”回路转动跟踪动力学模型为: (22) 式中:Js为平台舱的惯量矩阵;Tcs和Tns分别为微推进系统的控制力矩和平台舱的环境干扰力矩;ωsp表示平台舱本体坐标系相对于载荷舱本体坐标系的角速度。 根据式(16)和式(20)~(22)可以看出,“质量块—载荷舱”随动跟踪控制回路和“载荷舱—平台舱”随动跟踪控制回路动力学模型都属于二阶非线性系统。为了方便地将“质量块—载荷舱—平台舱”三体随动跟踪式重力卫星的动力学模型转化为状态方程的表达形式,将下标j=1、2、3、4进行如下定义:j=1为“质量块—载荷舱”平动跟踪动力学模型、j=2为“质量块—载荷舱”转动跟踪动力学模型、j=3为“载荷舱—平台舱”平动跟踪动力学模型、j=4为“载荷舱—平台舱”转动跟踪动力学模型。同时,定义状态变量为xj=[x1jx2jx3j]T,则状态方程可以表达为如下形式: (23) (24) (25) (26) (27) (28) (29) (30) 式中:bj为输入矩阵;uj为控制输入;fj(·)为非线性耦合项。 从式(25)~(28)可以看出,“质量块—载荷舱”回路和“载荷舱—平台舱”回路非线性耦合项的表达形式相似,因此文中采用相同的控制器来进行设计。 当前重力卫星控制系统主流方法的核心设计理念是针对干扰的一级扩张观测与抑制[29]。团队近年来在该方向的研究发现,如果直接将该算法应用至本文控制系统中,对式(25)~(28)所示的非线性耦合项直接进行估计会引入过多误差,并且非线性控制频域参数整定也难以直接配置。因此,为了获得更好的控制性能,文中在一级扩张观测与抑制方法的基础上,将控制输入误差定义为待估中间变量,构建了一种基于带宽参数化自适应补偿的复合自抗扰控制算法。 在控制器设计中,式(25)~(28)所示的非线性耦合项通常通过扩张状态观测器进行解耦,因此,“质量块—载荷舱—平台舱”三体随动跟踪式重力卫星总的控制器设计可以转化为12个独立的控制器设计。与此同时,由于式(25)~(28)所示的非线性耦合项表达形式相似,这12个独立的控制器的表达形式也一致。因此,为了简化控制器的描述,此处开始省略下标j,则每个控制器的状态方程和观测方程为: (31) 式中:y为输出变量。 扩张状态观测器可以表达为: (32) (33) 式中:z1,z2,z3用于估计x1,x2,x3;β1,β2,β3分别表示观测器参数;l1和l2分别表示控制参数。 定义系统误差为ek=xk-zk(k=1,2,3),则系统误差的导数可表示为: (34) 通常,该系统只有在式(25)~(28)所示的非线性耦合项的导数有界,且由观测器参数组成的增益矩阵是Hurwitz稳定的情况下才稳定。显然,对于上述非线性耦合项,很难直接在频域内配置控制器参数并获得理想的控制性能[30]。因此,为了提高控制性能,定义以下控制输入误差为中间变量: V=l2e1+l1e2+e3 (35) 将式(35)代入式(31)的第二项,得到如下关系: (36) 此时,定义新的状态变量为X1=x1,X2=x2,X3=-l2x1-l1x2,则控制输入误差校正的状态方程和观测方程可以表达为: (37) 式中:D表示新状态X3的导数。 因此,可对控制输入误差进行如下估计和补偿: (38) V=-K2Z1-K1·Z2-Z3 (39) 式中:Z1,Z2,Z3用于估计X1,X2,X3;B1,B2,B3分别表示新观测器参数;K1和K2分别表示控制输入误差的校正参数。 将控制输入误差校正的系统误差定义为Ek=Xk-Zk(k=1,2,3),则可得控制输入误差校正的误差方程及其传递函数H1(s): (40) (41) 同时,将式(39)代入式(37),对状态变量X3求导: (42) (43) 显然,式(41)和式(43)构成负反馈结构,框图如图5所示,并且当下列方程的极点位于左半平面时,可以保证稳定性。 s(l1s+l2)(s2+(B1+K1)s+B1K1+B2+K2)+ (s2+K1s+K2)(s3+B1s2+B2s+B3)=0 (44) 图5 负反馈结构框图Fig.5 Block diagram of negative feedback structure 可以看出,式(37)~(39)所示用于控制输入误差校正的扩张状态观测器属于线性二阶系统,因此,采用下列方程所示带宽参数化便可保证系统稳定性。 (45) (46) 式中:ω0为观测器带宽;ωc为控制带宽。 将式(46)中的带宽参数化代入H1(s),有: (47) 因此,存在ω∈[0,+∞),满足: (48) 由于: (49) 因此,存在ω0>0,使得: (50) 与此同时,由于H2(jω)在区间ω∈[0,+∞)内有界,即存在γ>0,满足: |H2(jω)|<γ,∀ω∈[0,+∞) (51) 因此,存在ω∈[0,+∞),当ω0>0时存在以下不等式: |H1(jω)H2(jω)|≤|H1(jω)||H2(jω)|<1 (52) 也就是说,-H1(s)H2(s) Nyquist曲线的幅值始终小于1,该曲线不包围-1点,再考虑到-H1(s)H2(s)在右半平面无极点,这说明了式(45)~(46)所示的带宽参数化可实现待估计中间变量的自适应补偿。 根据三体随动跟踪式重力卫星总体架构设计及其动力学建模可得出,质量块虽置于真空腔中,但仍存在辐射计效应、残余气阻等产生的加速度噪声及电容传感噪声干扰,同时,载荷舱和平台舱存在测量敏感器和执行器噪声的干扰。为了与现有激光测距低低卫卫跟踪重力卫星的性能进行对比,验证三体随动跟踪式重力卫星架构设计相比传统重力卫星架构的优势,以及姿态与无拖曳一体化复合自抗扰控制算法相比传统重力卫星一级干扰观测与抑制算法的有效性,卫星轨道、质量块干扰噪声、定姿定轨精度等指标与文献[5]一致,仿真条件如表2所示。 由于三体随动跟踪式重力卫星SCA和SCB的仿真结果一致,因此本文只给出SCA卫星的仿真结果并对其进行分析。 根据控制器的设计可以得出,对于载荷舱的复合自抗扰控制,若观测器带宽设计为一个更高的值可以使响应速度更快,但会引入过多的噪声。因此,为了与重力场的分辨率相匹配,在仿真中将观测器带宽配置为1.3节所示的中频段的截止频率,以保证稳定性。 表2 卫星基本参数及干扰噪声Table 2 Parameters of the satellite and disturbance noise 1)总体架构设计有效性仿真对比 本文重力卫星架构设计中,以质量块为参考基准,采用电容式传感器测量载荷舱与质量块间相对位姿信息,并通过非接触洛伦兹力执行器控制载荷舱跟踪质量块,实现高精度质心波动控制,仿真结果如图6所示。 从仿真结果可以得出,在5 mHz~0.1 Hz频段内,采用复合自抗扰控制方法,载荷舱相对质量块的质心波动控制精度为1×10-6m·Hz-0.5量级,相比传统重力卫星质心标定与调整方法提高了2个数量级,相比一级扩张观测与抑制方法,由于复合自抗扰控制方法将控制输入误差定义为待估中间变量进行误差补偿校正,精度可提高1个数量级,且对特定频带的谐振峰有一定的抑制效果。显然,该方法不需要质心标定与调整,且由于非接触洛伦兹力作为执行器控制,不存在微推进导致的质心波动问题,因此将更有利于后续地球重力场反演。 图6 载荷舱相对质量块质心波动控制Fig.6 Fluctuation of the center of mass for the payload module relative to the test mass 图7 平台舱相对载荷舱姿态角控制Fig.7 Attitude angle of the service module relative to the payload module 图8 平台舱相对载荷舱位置控制Fig.8 Position of the service module relative to the payload module 与此同时,平台舱为载荷舱提供电源通信保障,只需在非接触洛伦兹力执行器线性域运动范围内避免与载荷舱碰撞即可。平台舱相对载荷舱姿态与位置控制精度仿真如图7和图8所示。从仿真结果可得,在5 mHz~0.1 Hz频段内,平台舱相对载荷舱的姿态角和相对位置控制精度可达1×10-4rad·Hz-0.5和1×10-4m·Hz-0.5量级,满足非接触洛伦兹力执行器控制输入的线性域要求,并且不会产生两舱之间的碰撞。 2)姿态与无拖曳控制算法仿真对比 相比传统重力卫星,三体随动跟踪式重力卫星采用非接触洛伦兹力执行器作为执行机构实现姿态与无拖曳一体化控制,通过基于带宽参数化自适应补偿的复合自抗扰控制算法提高频域控制性能,载荷舱的姿态与无拖曳控制仿真结果如图9~12所示。 图9 载荷舱姿态指向控制精度Fig.9 Attitude pointing control accuracy of the payload module 图10 载荷舱姿态稳定度Fig.10 Attitude stability of the payload module 图11 载荷舱角无拖曳控制Fig.11 Angle drag-free control of the payload module 图12 载荷舱线无拖曳控制Fig.12 Line drag-free control of the payload module 从仿真结果可以得出,在5 mHz~0.1 Hz频段内,基于带宽参数化自适应补偿的复合自抗扰控制方法的载荷舱姿态指向控制水平优于1×10-5rad·Hz-0.5,姿态稳定度优于1×10-6rad·s-1·Hz-0.5,线无拖曳控制水平优于2×10-9m·s-2·Hz-0.5,角无拖曳控制水平优于1×10-8rad·s-2·Hz-0.5量级。各关键指标仿真结果相比传统一级干扰观测与抑制方法高1-2个数量级。上述仿真有效验证了基于带宽参数化自适应补偿的复合自抗扰控制算法的有效性。 根据上述仿真结果可以得出,文中所提的“质量块—载荷舱—平台舱”三体随动跟踪式重力卫星架构及其基于带宽参数化自适应补偿的复合自抗扰控制方法可实现如表1所示的下一代激光测距低低卫卫跟踪重力卫星平台的关键技术指标要求。 本文将非接触卫星平台推广应用至下一代激光测距低低卫卫跟踪重力卫星中,提出了一种以质量块为参考基准的“质量块—载荷舱—平台舱”三体随动跟踪式重力卫星构架,并构建了一种基于带宽参数化自适应补偿的复合自抗扰控制方法,用于该架构下的姿轨耦合控制。相比传统重力卫星采用的一级扩张观测与抑制,该方法将控制输入误差定义为待估中间变量抑制姿轨耦合动力学非线性耦合项的影响,并基于带宽参数化方法有效提升了姿态环路的姿态指向精度、姿态稳定度和角无拖曳水平以及位置环路的质心波动和线无拖曳水平的频域控制性能,可为未来高精度地球重力场测量提供一种技术手段。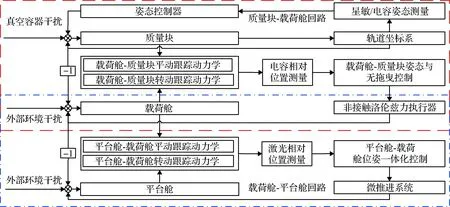
2 动力学建模
2.1 “质量块—载荷舱”回路动力学建模
2.2 “载荷舱—平台舱”回路动力学建模
3 控制器设计
3.1 状态方程建立
3.2 复合自抗扰控制
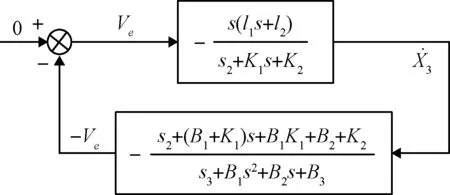
3.3 带宽参数化稳定性分析
4 仿真分析
4.1 仿真初始条件
4.2 仿真结果与分析

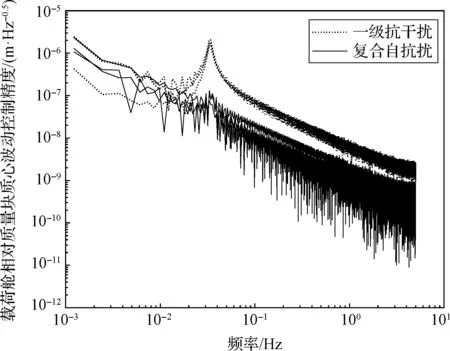




5 结 论
