考虑“桩-土结构相互作用”的拱桥时程分析

贺效强

(山西省交通规划勘察设计院有限公司 太原市 030032)

0 引言

地震是一种严重危害人民生命财产安全的自然灾害现象，因此对于大跨径桥梁而言，结构抗震性能的重要性不言而喻[1-3]。在地震分析时通常采用迈达斯Civil有限元建模分析的方法，人们通常选择仅建立桥梁上部结构有限元模型而忽略桥梁基础作用，该种方法具有简便、高效、力学概念清晰的优势，但却忽略基础中的“桩-土结构相互作用”对桥梁力学性能的影响。

我国桥梁规范中对桥梁结构在地震作用下的分析，都采用的是桥墩固接模型，但是其具有显著的劣势：忽略了桩-土相互作用及桩-土-结构的相互作用而把整个基础的抗弯刚度简单地集中到桥墩的底部。通过已有的工程实例不难总结出，实际工程分析的结果与桥墩固接模型分析出的结果两者之间是有很大差别的。这是由于实际工程中桥梁上部结构、承台、桩基及桩周基础是一个共同工作的整体性，且桩-土相互作用具有一定的非线性特性，此外桩-土接触截面还具有相对滑移、分离、错位等复杂现象[4-6]。因此，传统的墩底固结方法无法真实地反映桥梁结构真实的力学状态。

以某跨径为82.0m的下承式混凝土拱桥为依托工程，建立迈达斯Civil有限元模型，分析了是否考虑“桩-土结构相互作用”对桥梁结构力学性能的影响。

1 “桩-土结构相互作用”简介

桩基础可在一定程度上影响桥梁在地震作用下的结构响应性能，因此“桩-土-结构”相互作用对桥梁地震响应的影响分析应该成为我们关注的重点。

目前，“桩-土-结构”的相互作用理论主要有：荷载传递法、弹性理论法、剪切位移法、有限单元法、边界单元法。现阶段的桥梁抗震分析多采用有限元模拟法，大跨径桥梁由于其桩基较多，因此如果采用实体有限元单位模拟土体将会使得模型过大，计算耗时过多。因此首先建立桩基础有限元模型，然后采用等代弹簧代替桩基础周围的土体作用。土弹簧刚度根据土层的m值进行计算，土弹簧的刚度计算公式如式(1)所示：

K=a×b×m×z

(1)

式中：a为土层厚度；b为桩的计算宽度；m为地基土的刚度系数；z为土层的深度。

由于桥梁形式为下承式拱桥，因此在考虑桥梁的“桩-土-结构”相互作用时，主要通过改变拱肋边界条件来实现。具体表现为：首先采用梁单元模拟拱肋与土体接触部分，然后对拱肋底部进行固结处理，并且对与土体接触的拱肋单元顺桥向、横桥向进行弹性连接模拟，土弹簧的刚度计算如式(1)所示。

2 工程概况

该桥梁结构形式为下承式混凝土拱桥，桥梁跨径为82.0m，拱肋高度为18.0m，桥梁矢跨比为0.22，桥梁横向宽度为28.0m。桥面采用10根混凝土梁组成，横向由多根横向联系进行连接，梁截面尺寸为0.25m×3.1m，为抵抗较大的剪力，混凝土梁在边跨进行了截面增大。拱肋采用混凝土拱，其截面尺寸为1.4m×1.6m，拱肋间采用5根横系梁进行连接，横系梁材料类型为16Mn。吊杆采用的材料类型为Strand1860，其截面形式为圆形，圆直径为0.073m，桥梁正立面如图1所示。

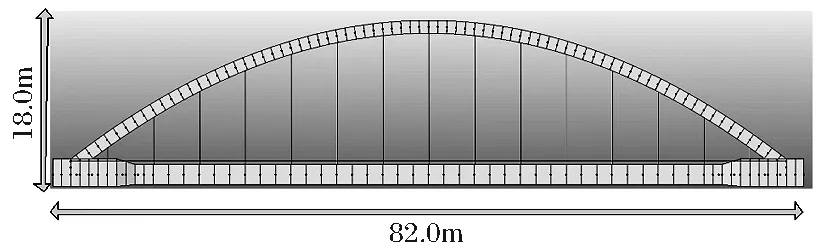
图1 桥梁正立面图

该桥梁的主要设计标准如下：

(1)道路等级：城市Ⅰ级主干道。

(2)设计车速：60km/h。

(3)设计荷载：城市A 级。

(4)道路荷载标准：BZZ-100 标准车。

(5)桥梁设计基准期：100年。

(6)桥梁设计使用年限：100年。

(7)桥梁安全等级：一级。

(8)设计基准风速V10=20.08m/E；抗震设计：地震动峰值加速度为0.05g。

(9)设计洪水频率：300 年一遇，设计水位42.81m。

3 数值模型的建立

利用迈达斯Civil建立该桥梁的有限元模型，全桥可离散为735个节点，927个梁单元，桥梁有限元模型建立结果如图2所示，不考虑“桩-土结构相互作用”的桥梁边界条件如图3所示，主梁与基础土体连接部分采用固结的方式考虑。桥梁的材料参数如表1所示。

桥梁全桥共采用三种材料，其中C50用于拱肋及主梁，弹性模量取值34500000kN/m2，材料容重取值为25.0kN/m3。Strand1860主要用于吊杆，其弹性模量取值为195000000kN/m2，容重取值为78.5kN/m3，系梁采用16Mn，弹性模量取值为210000000kN/m2，容重取值为76.98 kN/m3。

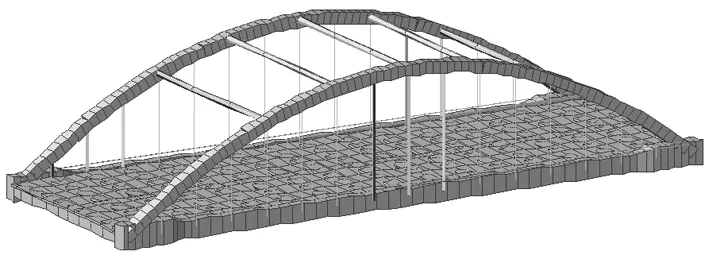
图2 桥梁有限元模型

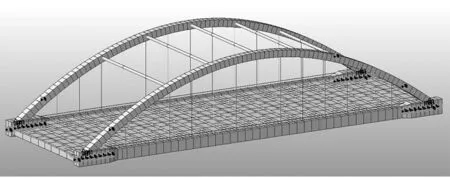
图3 桥梁边界条件

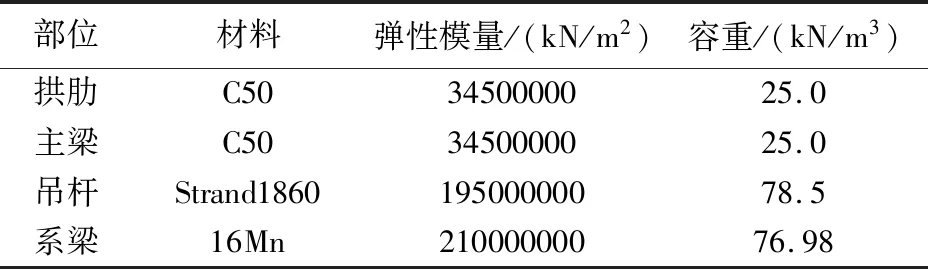
表1 桥梁材料参数表

本次地震波时程输入数据如图4所示，在荷载/时程分析数据/时程荷载工况中可定义荷载工况，荷载工况及阻尼比的输入步骤及数据如下：

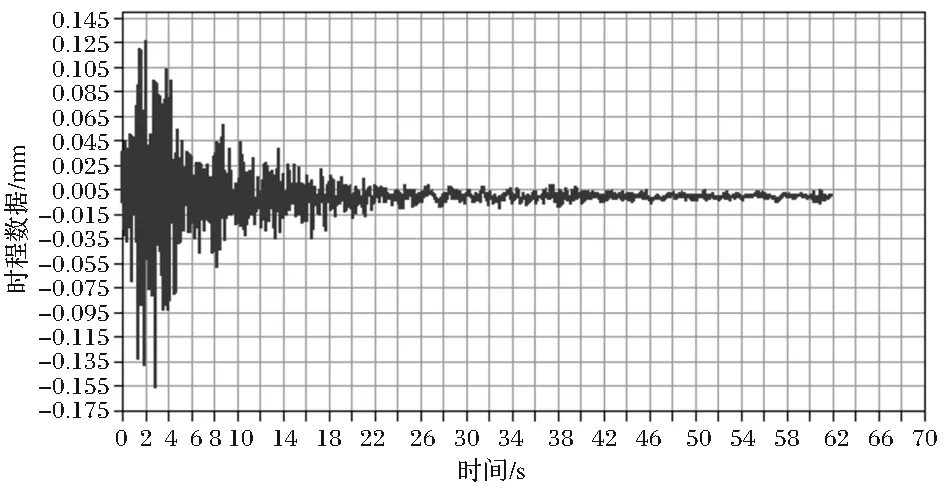
图4 地震波时程

(1)结束时间：指地震波的分析时间，依据地震波，地震波的分析时间取52s。

(2)分析时间步长：表示在地震波上取值的步长，为尽可能地获取更多桥梁在地震作用下的结构响应，可取2。

(3)输出时间步长：指整理结构时输出的时间步长，取26。

(4)分析类型：由于本桥梁模型中具有非线性边界条件，因此选择非线性分析。

(5)分析方法：由于该桥梁自振周期较大，采取直接积分法。

(6)时程分析类型：由于地震波为非协振函数，因此时程分析类型选择线性瞬态。

(7)振型阻尼比：根据《城市桥梁抗震设计规范》(CJJ 166—2011)，斜拉桥阻尼比数值建议采用0.03。

4 结果分析

4.1 静力分析结果

为对该桥梁力学性能进行全面地分析，首先对该桥梁的承载力极限状态进行了计算分析评估，计算了不考虑“桩-土结构相互作用”、考虑“桩-土结构相互作用”两种工况。由于桥梁跨中截面力学性能具有较强的代表性，因此提取了跨中截面的桥梁承载能力极限状态下的力学性能参数如表2所示，分析表2最终可得到以下结论：

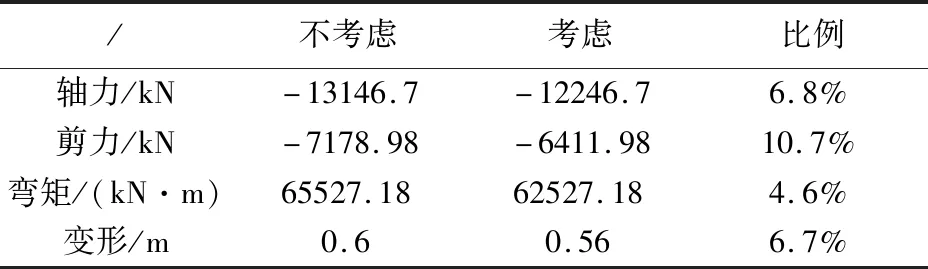
表2 桥梁承载力极限状态跨中截面力学性能

(1)两种工况下跨中截面轴力数值分别为-13146.7kN、-11246.7kN，考虑“桩-土结构相互作用”可将轴力降低6.8%。

(2)两种工况下跨中截面剪力数值分别为-7178.98kN、-6411.98kN，考虑“桩-土结构相互作用”可将剪力降低10.7%。

(3)两种工况下跨中截面弯矩数值分别为65527.18 kN.m、62527.18 kN.m，考虑“桩-土结构相互作用”可将弯矩降低4.6%。

(4)两种工况下跨中截面挠度数值分别为0.6m、0.56m，考虑“桩-土结构相互作用”可将变形降低6.7%。

由上述分析可知：当桥梁考虑“桩-土结构相互作用”时，桥梁结构在静力荷载工况作用下的结构内力及变形均有一定程度的减小，这是因为在有限元结构的建模过程中，如不考虑“桩-土结构相互作用”，一般的处理方式为在基础底部采用固结的边界条件方式，这种做法实际上是偏安全的考虑了结构的边界条件。

4.2 时程分析结果

分别对两种工况进行地震时程分析，提取计算结果如图5～图7所示。

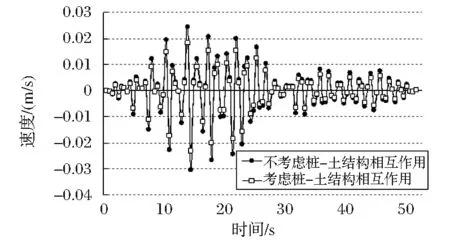
图5 跨中截面速度时程图

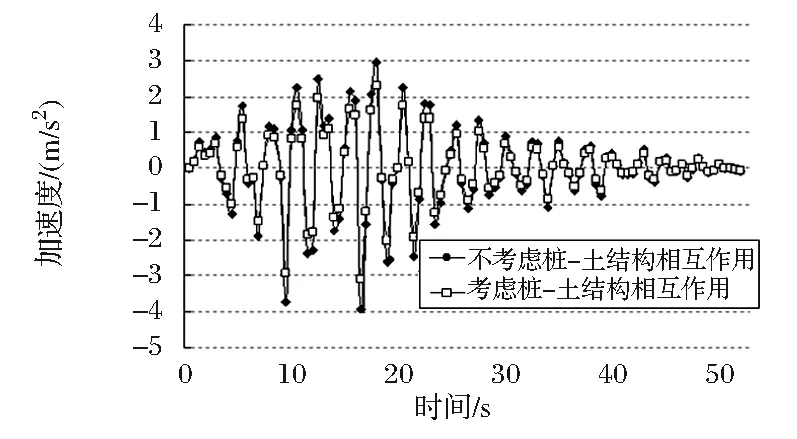
图6 跨中截面加速度时程图

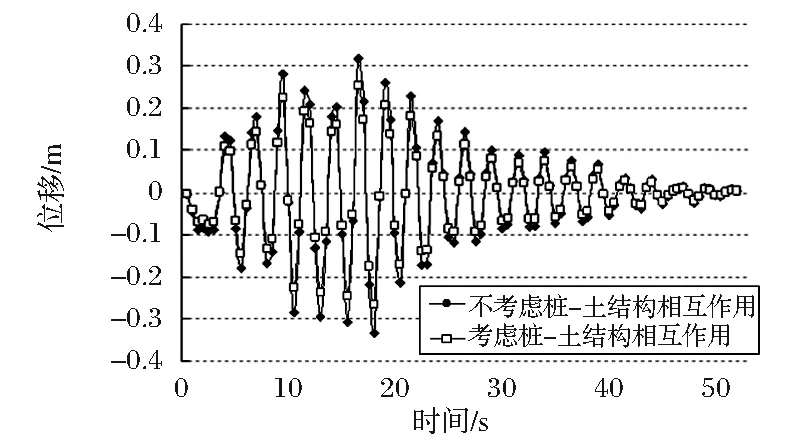
图7 跨中截面位移时程图

从图5～图7可得到以下结论：

(1)当考虑“桩-土结构相互作用”后，桥梁的时程分析结果幅值均有所降低，尤其以8～25s段的幅值下降最为明显，但时程分析初段、终段并不明显；

(2)分析8～25s的时程分析，当考虑“桩-土结构相互作用”后，跨中截面速度峰值可下降18.5%，跨中截面加速度峰值可下降21.8%，跨中截面挠度峰值可下降20.1%。

5 结语

以某跨径为82.0m的下承式混凝土拱桥为依托工程，建立迈达斯Civil有限元模型，分析了是否考虑“桩-土结构相互作用”对桥梁结构力学性能的影响结果，分析最终可得：

(1)考虑“桩-土结构相互作用”可将轴力降低6.8%、可将剪力降低10.7%、可将弯矩降低4.6%、可将变形降低6.7%。

(2)考虑“桩-土结构相互作用”后桥梁结构在静力荷载工况作用下的结构内力及变形均有一定程度的减小，这是因为在有限元结构的建模过程中，如不考虑“桩-土结构相互作用”，一般的处理方式为在基础底部采用固结的边界条件方式，这种做法实际上是偏安全地考虑了结构的边界条件。

(3)当考虑“桩-土结构相互作用”后，桥梁的时程分析结果幅值均有所降低，尤其以8～25s段的幅值下降最为明显，但时程分析初段、终段并不明显。

(4)分析8～25s的时程分析，当考虑“桩-土结构相互作用”后，跨中截面速度峰值可下降18.5%，跨中截面加速度峰值可下降21.8%，跨中截面挠度峰值可下降20.1%。

(5)在工程中通常采用简化边界条件的方式来模拟桥梁下部结构与基础间的连接作用，但本文的研究结果表明该种简化方式对计算结果有一定的影响，因此建议后续此类工程的有限元计算分析中应考虑“桩-土结构相互作用”。