光学观测中几种太阳夹角计算方法及精度分析
2022-12-26虞炳文娄广国蔡红维周小杰
虞炳文,娄广国,蔡红维,周小杰,杨 宏
(西昌卫星发射中心,四川 西昌 615000)
0 引言
在航天发射、低轨卫星长期在轨运行管理,以及天文观测中,光学观测是一个重要且不可或缺的的观测方式,光学观测具备别的测量控制设备所不具备的优势,比如直观,在光学影像中,可以很直观的看见飞行器的外部状态,另外,光学观测的测角精度较高,可以作为飞行器在空间中位置的一个重要参考量。尤其在航天发射的起飞阶段中,光学观测设备是重要的辅助决策判决的手段,在发射场中得到了大量的运用。但是制约光学设备使用并发挥作用的限制条件也较为明显,除了包括山体、云等遮蔽物之外,直面部分强光源的物体的直射,可能会对光学设备的感光模块造成不可逆转的破坏,其中较为明显的,就是太阳以及月球的光线直射,因此,如何通过准确计算出飞行器与太阳的夹角,以达到有效规避强光直射的风险,避免太阳对光学设备的损坏,是文中将要论述的重点。
在计算飞行器与太阳夹角的过程中,有很多的算子可供选择,可区分为简单算子和复杂算子,简单算子的优势是只需要少量的参数即可计算出结果,但是精度相对较低,复杂算子的优势是计算精度高,但是其需要装填的参数较多,甚至有些参数需要专业设备才能测得,在日常使用中并不便捷。因此在日常使用中,通常会选用精度较高的简单算子来替代复杂算子,本文将通过计算及精度分析,论证简单算子中与复杂算子计算结果最为接近的算子组合,以达到在简单便捷使用的同时,又能保证一定的精度。
1 计算太阳赤纬及太阳时角
首先需要介绍一下什么是太阳赤纬及太阳时角。
1.1 太阳赤纬和时角的基本概念
要梳理清楚什么是太阳赤纬和时角,需要首先建立天球这个天文学概念。
1.1.1 天球坐标系的概念
首先需要理解的是,天球是一个无限大的球体,距离在这里没有意义,在天球坐标系中,天球的中心可以是任何的星球,虽然一般情况下,会将地球放在天球的中心。换言之,地球在天球的中心位置,此时的天球可以理解成,地球居民在地球上的观察视角,在某个位置,如果足够高,四周没有遮挡,观察者所能看见的就是半个天穹,即以观察者所在位置为切点的,与地球球体相切的一个无限延展的平面,理论上,因为观察者所观察的是整个宇宙,距离无穷远,此时观察者所站立的地球,其本身的半径相比较无穷大而言,可以忽略不计,因此,此时整个宇宙的所有星球,都可以区分为两种位置,一种是平面以上,一种是平面以下。
因此,可以简单地认为,观察者在任何一个位置,都能观察到其所在切平面以上的,即半个宇宙的所有星球,因为很难去准确知晓某个星球距离地球的位置,所以在天球坐标系中需要将距离的概念淡化,而淡化距离概念的最简单直接的方法,就是将所有的星球与地球的距离都假设成相同,即将所有的星球都放在同一个球面上,当忽略了距离,此时想要标识某个星球的位置,就只需要用到两个参数值,即一个用来标识其纵向上的位置,一个用来标识其横向上的位置的数值。
在天球坐标系中,选用何种标准来标识一个方位和一个俯仰上的值,其最简单直接的想法便是,既然都是球体,日常用来标识地球球体的经纬度体系,可否用来标识天球的度量体系?原理上是可以的,事实上也正是如此的。因此在天球坐标系的度量体系中,实际上选用了一套和地球大地坐标系同样的度量方式,区别在于地球坐标系中使用的经纬度和高程,而在天球坐标系中因为淡化了距离的概念,将所有的星球都假设在了同一距离的球面上,所以并不需要高程这一参数值,因为需要高程的地方所需的一个基本特征是能够测量高程,而在宇宙尺度下,距离是很难被获取的。将星球的距离都假设在同一个平面上的过程,也就是常说的投影。天球坐标系仅仅参考了地球大地坐标系的经纬度值,在天球坐标系中,这两个参数值被称之为赤经和赤纬。
在天球坐标系中,天球的中心是地球的中心。因为观察者虽然并不在地球中心观察,但是因为观察者所在的地球表面,其距离地球中心的距离,相比较天球无限大的距离来说,可以忽略不记,因此可以简单认为,观察者所在的位置就是地球中心。
1.1.2 天球坐标系
同样一个天球,根据定义的经过球心的水平面不同,可以区分为多种天球坐标系,在此重点介绍常见的天球坐标系有三种。
首先是经过球心的平面为赤道面时,该处所指赤道便是地球赤道经过往外无限延伸,最终势必将会与天球相交,此时便形成了第二赤道坐标系,此时的赤道面称之为天赤道,经地心,作一条与天赤道垂直的无限延长的线,与天球相交于两点,即图 1中所示P点(天北极)与P′点(天南极)。
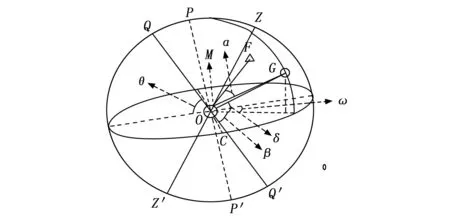
图1 天球示意图
然后是将地球与太阳放在同一个平面上,所形成的平面,称之为黄道面,以此为基准,便是黄道坐标系,仅靠地球与太阳两点不能确认一个平面,还需要一到两个点,这另外两个点的选择,便是春分点和秋分点,即太阳直射点穿过赤道时的两个点。经过地心,作一条与黄道面垂直的直线,与天球相交于两点,便是图 1中的Q(黄北极)和Q′(黄南极)点。黄道面与赤道面相交所形成的夹角,便是黄赤交角。
最后还需要介绍的便是以观察者所在位置,所作的与地球相交的平面,称之为地平面,此时的地平面,在宇宙维度内,可以认为是经过地球地心的一个平面,过地心作一条垂直于地平面的直线,与天球相交于两点,即观察者的头顶与脚底,见图1中Z(天顶)和Z′(天底)。
1.1.3 对天球上的常用点线面的理解
对图 1中所涉及的标注进行解释。
F点指的是飞行器,G点指的时太阳,飞行器在此时,也可以当成一个映射在天球球面上的物体,M点为地球上观察者的位置,过天北极P点与天南极P′的赤经圈称之为天子午圈,天子午圈可以有很多条,但是通过天顶Z的,只有一个圈,称之为本初子午圈,即图 1中所画弧线PZP′所在圆。
C点为春分点,需要重点介绍一下,在后续计算过程中,很多的运算的数值,都与此概念相关。春分点时黄道面和赤道面的相交点,即太阳直射点从南向北经过赤道的那个点,这个点并不是一个实际上地球地理坐标点,是无法用经纬度表示的,春分点是两个平面的交点,始终处在两个平面的相交处。天文学上,将春分点作为很多天文概念的起算点,比如恒星时,比如太阳赤经。
太阳赤纬角为地心与太阳的连线与天赤道面的夹角,即图 1中δ角。
太阳赤经角,从春分点C向东,一直到太阳在天赤道上的投影线之间的夹角,即春分点所在的赤经圈与太阳所在的赤经圈之间的夹角,称之为赤经角,即图 1中的β角。
太阳时角,是从本初子午圈与天赤道相交的点向西,即太阳所在的赤经圈与本初子午圈之间的夹角,即图 1中的γ角。
最终需要求解的是太阳夹角,即从地球上某个位置观察飞行器和太阳时,太阳和飞行器之间的夹角,即图 1中的α角。
在此需要特别注意的是,上述涉及的天文概念中,前缀往往都带着参考的星球的名称,比如太阳,之所以这么解释,是因为可以不是太阳,可以是宇宙中任何一个天体,比如银河系的中心作为参考的银河坐标系。在本文中所涉及的未特别声明的天文概念,均以太阳作为参考。
1.2 太阳赤纬的计算方法
要计算太阳夹角,首先需要解决的问题,便是如何准确计算天球坐标系下,太阳赤纬及太阳时角的值。首先计算太阳赤纬的值。
计算太阳赤纬值的方法有很多,常见的简单算法有Cooper算法、Spencer算法、Stine算法、Bourges算法、Wang算法、Yu算法,上述六种算法均基于天文观测数据,通过公式拟合提出的数学公式,另外还可以通过对天文观测数据的数值拟合算法,求出拟合度更高的计算公式,只是通过该方法提出的公式,其系数会因年而异,所以不具备普适性,另外,李文提出通过傅里叶展开法提出对拟合公式的改进算法。除数学拟合算法之外,还有一种基于VSOP87行星理论,演算推导算法的方法。
下面结合C++代码语言,对太阳赤纬各算法进行逐个分析计算。
1.2.1 Bourges算子
Bourges是由Bourges提出的,Bourges算子的公式如下所示。其中ω为弧度参考系数,t为等效计日序数。太阳赤纬角的单位为弧度。
δ=0.3723+23.2567sin(ωt)+0.1149sin(2ωt)-0.1712sin(3ωt)-0.7580cos(ωt)+0.3656cos(2ωt)+0.02010cos(3ωt)
(1)
弧度参考系数如下所示:
(2)
计日序数的计算如下所示。其中dn为计日序数,即本年度的第几天。
t=dn-1-n0
(3)
n0的的计算公式如下,其中n表示年份,如本年度为2022年,则n=2022。
n0=78.801+[0.2422(n-1969)]-int[0.25(n-1969)]
(4)
Bourges算法实现的代码如下:
double Bourges(cDateTime date)
{
int n=getDaysOfYear(date);
int temp=0.25*(date.year-1969);
double n0=78.801+0.2422*(date.year-1969)-temp;
double t=n-1-n0;//等效计日序数
double w=2*M_PI/365.2422;//参考弧度系数
double dellta=0.3723+23.2567*sin(w*t)+0.1149*sin(2*w*t)-0.1712*sin(3*w*t)-0.7580*cos(w*t)+0.3656*cos(2*w*t)+0.0201*cos(3*w*t);
return dellta/180.0*M_PI;//弧度
}
1.2.2 Cooper算子
Cooper算子是由Cooper提出的,Cooper算子的公式如下所示。公式中n为该年度中的天数累计值,如1月11日,则n=11。太阳赤纬角的返回值单位是弧度。
(5)
δ为太阳赤纬角。代码实现如下:
double Cooper(cDateTime date)
{
int n=getDaysOfYear(date);
double dellta;
dellta=23.45*sin(2*M_PI*(284.0+n)/365.0);
return dellta/180.0*M_PI;//弧度
}
1.2.3 Spencer算子
Spencer算子是由Spencer提出的,其中太阳赤纬角的单位为弧度,θ为日角。算法公式如下所示:
δ=0.006918-0.399912cos(θ)+0.070257sin(θ)-0.006758cos(2θ)+0.000907sin(2θ)-0.002697cos(3θ)+0.00148sin(3θ)
日角的计算公式如下所示:
(6)
Spencer算子的实现代码如下:
double Spencer(cDateTime date)
{
int n=getDaysOfYear(date);
double gamma=2*M_PI*(n-1)/365.0;//日角
double dellta=0.006918-0.399912*cos(gamma)+0.070257*sin(gamma)-0.006758*cos(2*gamma)+0.000907*sin(2*gamma)-0.002697*cos(3*gamma)+0.00148*sin(3*gamma);
return dellta;//弧度
}
1.2.4 Yu算子
Yu算子是由Yu提出来的,是在Spencer算子的基础上做的简化,计算得到的太阳赤纬角单位为弧度。θ为日角,公式如下:
δ=0.006918-0.399912cos(θ)+0.070257sin(θ)-0.006758cos(2θ)+0.000907sin(2θ)
(7)
其中的日角的计算公式如下:
(8)
实现Yu算法的代码如下:
double Yu(cDateTime date)
{
int n=getDaysOfYear(date);
double theT=2*M_PI*(n-1)/365;//日角
double dellta=0.006918-0.399912*cos(theT)+0.070257*sin(theT)-0.006758*cos(2*theT)+0.000907*sin(2*theT);
return dellta;//弧度
}
1.2.5 Stine算子
Stine算子是由Stine提出的,其中太阳赤纬角的单位为弧度,其中n为计日序数,即本年度的第几天。
Stine算法的实现代码如下:
double Stine(cDateTime date)
{
int n=getDaysOfYear(date);
double dellta=asin(0.39795*cos(2*M_PI*(n-173)/365.242));
return dellta;//弧度
}
1.2.6 Wang算子
Wang算子是由王炳忠在Bourges的基础上,针对计日系数,修改了部分系数,并将起算年份从1969改为了1985,使得其更加贴近真实值。计算所得的太阳赤纬角的单位为弧度。公式如下所示,与Bourges算子相同。太阳赤纬角的单位为弧度。
δ=0.3723+23.2567sin(ωt)+0.1149sin(2ωt)-0.1712sin(3ωt)-0.7580cos(ωt)+0.3656cos(2ωt)+0.02010cos(3ωt)
(9)
其中的弧度参考系数也与Bourges相同。如下所示:
(10)
以及等效计日序数的算法也是相同的,如下:
t=dn-1-n0
(11)
与Bourges不同的是对n0的计算,如下所示:
n0=79.6764+[0.2422(n-1985)]-int[0.25(n-1985)]
(12)
Wang算法的实现代码如下所示:
double Wang(cDateTime date)
{
int n=getDaysOfYear(date);
int year=date.year;
int temp=0.25*(year-1985);
double n0=79.6764+0.2422*(year-1985)-temp;
double t=n-1-n0;//等效计日序数
double w=2*M_PI/365.2422;//参考弧度系数
double dellta=0.3723+23.2567*sin(w*t)+0.1149*sin(2*w*t)-0.1712*sin(3*w*t)-0.7580*cos(w*t)+0.3656*cos(2*w*t)+0.0201*cos(3*w*t);
return dellta/180.0*M_PI;//弧度
}
1.2.7 数值拟合法
数值拟合法是由李文提出的,根据2015年-2018年的天文年历,提出使用积日因子β作为多项式的中间系数,进行拟合计算。得到适2015-2018年的年份的改进公式。
太阳赤纬角的单位为弧度,其中太阳赤纬角的计算公式如下,其中的β为积日因子,ak为系数。
(13)
积日因子的求解公式如下所示。其中dn为积日系数。
(14)
n0的计算公式如下所示:
n0=79.6764+0.2422(n-1985)-int(n-1985)
(15)
数值拟合算法的代码如下所示:
double NumericalFitting(cDateTime date)
{
int n=getDaysOfYear(date);
int year=date.year;
int temp=year-1985;
double n0=79.6764+0.2422*(year-1985)-temp;
double b=2*M_PI*(n-1-n0)/365.2422;
int L=(year-2015)%4;
double dellta=0;
if(L==0)
{
dellta=calDellta(b,0.38835,22.911,-0.49055,-3.1217,0.043485,-0.19959,0.12879,0.045704,-0.040516,0.010031,-1.0946e-3,4.5142e-5);
}else if(L==1){
dellta=calDellta(b,0.38879,22.909,-0.49009,-3.1203,0.041657,-0.19950,0.12971,0.045246,-0.040482,0.010056,-1.1011e-3,4.5598e-5);
}else if(L==2){
dellta=calDellta(b,0.38769,22.909,-0.49277,-3.1178,0.046562,-0.20471,0.12953,0.047321,-0.041560,0.010309,-1.1302e-3,4.6935e-5);
}else if(L==3){
dellta=calDellta(b,0.38702,22.910,-0.49060,-3.1193,0.044708,-0.20270,0.12943,0.046646,-0.041166,0.010207,-1.1175e-3,4.6298e-5);
}
return dellta/180.0*M_PI;//弧度
}
double calDellta(double b, double a0,double a1, double a2, double a3, double a4, double a5, double a6, double a7, double a8, double a9, double a10, double a11)
{
double dellta=a0*pow(b,0)+a1*pow(b,1)+a2*pow(b,2)+a3*pow(b,3)+a4*pow(b,4)+a5*pow(b,5)+a6*pow(b,6)+a7*pow(b,7)+a8*pow(b,8)+a9*pow(b,9)+a10*pow(b,10)+a11*pow(b,11);
return dellta;
}
1.2.8 傅里叶展开法
傅里叶展开法是由李文提出的,在数值拟合法的基础上,进行的改进算法,通过观察连续的太阳赤纬角的变化规律,发现太阳赤纬角的变化具备周期性,每4年一个循环,因此将算法的周期,从1年修改为4年,定义算法中的年份为每个周期中的第三年,并且将计日序数从之前的1年中的第几天,改成整个4年周期中的第几天,即总的计日序数。
得到的太阳赤纬角的值,单位为弧度,其中β为积日因子。计算公式如下所示:
(16)
积日因子的计算公式如下所示,其中dn为积日系数。
(17)
式中,n0表达式如下所示:
n0=79.6764+0.2422(n-1985)-int(n-1985)
(18)
傅里叶展开法的计算公式如下所示:
double FourierBaseNF(cDateTime date)
{
int n=getDaysOfYear(date);
int year=date.year;
int y=0;//周期内的第3个年份
int dn=0;//周期内的总计日序数
if(year>=2015)
{
y=((year-2015)/4)*4+2017;
}else{
y=2013-((2015-year)/4)*4;
}
int temp=(year-3)%4;//这是周期内的第几年
if(temp==0)
{
dn=n;
}else if(temp==1)
{
if(QDate::isLeapYear(year-1))
{
dn=dn+366;
}else {
dn=dn+365;
}
dn=dn+n;
}else if(temp==2)
{
if(QDate::isLeapYear(year-2))
{
dn=dn+366;
}else {
dn=dn+365;
}
if(QDate::isLeapYear(year-1))
{
dn=dn+366;
}else {
dn=dn+365;
}
dn=dn+n;
}else if(temp==3)
{
if(QDate::isLeapYear(year-3))
{
dn=dn+366;
}else {
dn=dn+365;
}
if(QDate::isLeapYear(year-2))
{
dn=dn+366;
}else {
dn=dn+365;
}
if(QDate::isLeapYear(year-1))
{
dn=dn+366;
}else {
dn=dn+365;
}
dn=dn+n;
}
double n0=79.6764+0.2422*(y-1985)-int(y-1985);
double b=2*M_PI*(dn-1-n0)/365.2422;
double dellta=calFourierBaseNF(b,0.3783,-0.5624,0.3654,0.0156,-0.007662,-0.0005366,23.25,0.1082,-0.1705,-0.002773,0.003393);
return dellta/180.0*M_PI;//弧度
}
double calFourierBaseNF(double b,double a0,double a1,double a2,double a3,double a4,double a5,double b1,double b2,double b3,double b4,double b5)
{
double dellta=a0+a1*cos(b)+a2*cos(2*b)+a3*cos(3*b)+a4*cos(4*b)+a5*cos(5*b)+b1*sin(b)+b2*sin(2*b)+b3*sin(3*b)+b4*sin(4*b)+b5*sin(5*b);
return dellta;
}
1.2.9 VSOP87行星理论
VSOP87理论是由Bretagnon和Francou在1987年提出的,是VSOP82理论的进一步完善,VSOP理论是用来描述太阳系范围内的行星的轨道,在很长时间内的周期性变化的一种半分析理论。
VSOP形形理论除了可以算出精确的行星轨道参数,还可以直接计算出行星的位置,在此所言的位置,包含各种坐标系在内,如黄道坐标系。
计算VSOP87计算太阳赤纬角的过程,大致可分为七步。
1)计算儒略日数,用J表示。
2)计算相对儒略实际数,用T表示,如下所示:
(19)
3)计算太阳几何平黄经,用L表示,如下所示:
L=280.466456+36000.76982779×T+0.003032028×
(20)
4)计算平黄赤交角,用MB表示,如下所示:
(21)
5)计算太阳平近点角,用MSs表示,如下所示:
MSs=357.52191+35999.0503×T-
(22)
6)计算太阳真黄经,用SYS表示,如下所示:
SYS=L+(1.9146-0.004817×T-0.000014×T2)
(23)
7)计算太阳地心赤纬角,用Dec表示,如下所示:
(24)
上式中涉及的radeg为弧度与度的转换量纲,取radeg值为57.295 779 513 07。
用代码实现上述公式如下:
double VSOP87(cDateTime date)
{
//儒略日数
double J=date2JD(date);
//计算相对儒略世纪数
double T=(J- 2451545.0)/36525;
//太阳几何平黄经
double L=280.466456+36000.76982779*T+0.003032028*pow(T,2)+pow(T,3)/49931-pow(T,5)/15299;
//平黄赤交角
double MB=23.4392911111-(46.815/3600)*T-(0.00059/3600)*pow(T,2)+(0.001813/3600)*pow(T,3);
//太阳平近点角
double MSs=357.52191+35999.0503*T-0.0001559*pow(T,2)-0.00000048*pow(T,3);
//太阳真黄经
double SYS=L+(1.9146-0.004817*T-0.000014*pow(T,2))*sin(MSs/radeg)+(0.019993-0.000101*T)*sin(2*MSs/radeg)+0.00029*sin(3*MSs/radeg);
//太阳地心赤纬
double Dec=asin(sin(MB/radeg)*sin(SYS/radeg));
return Dec;
}
1.3 太阳时角的计算方法
太阳时角是以太阳为参考,其值代表了观察者所在的子午圈与太阳所在的子午圈之间的夹角。太阳时角的单位通常可以是角度值,如度分秒,此时的取值范围为0至360度,也可以是时间值,如时分秒,此时的取值范围为0至24小时。当用角度表示时,其表示的含义可以理解为两个子午圈之间的夹角,当使用时分秒表示时,其含义可以理解为太阳在时角时间之前通过观察者正上空。如时角为3.5h,则代表在3.5小时之前,太阳在3.5小时之前从观察者所在的正上空通过。
太阳时角的计算采用下列公式。其中tS为真太阳时。
(25)
真太阳时的计算采用下面中的公式计算,其中t为平太阳时,单位为小时。在天文观测中,很多天文概念都会加一个“平”字,其含义往往是代表着未加误差修正的简单值,加上修正以后,通常称之为“真”。eot即对时间的修正值。太阳时角的计算,其重点就在于误差修正值eot的计算。
(26)
下面将介绍6种计算太阳时角的算子,分别为Lamm算子,Spencer算子,Whillier算子,Wloof算子,Yu算子,以及VSOP87行星理论。其区别主要便在误差修正值的计算上。
1.3.1 Lamm算子
Lamm算子是由Lamm提出的,其特点是考虑了平年和闰年的区别,其公式如下。以四年为一个周期,其中n为全周期中的计日序数。Ak和Bk为系数值,在此采用杜春旭提出的参数值进行计算。计算所得eot值单位为分钟值,需要转化为小时进行下一步计算。
(27)
实现代码如下所示:
double Lamm(cDateTime mDateTime, double lon)
{
int n=getDaysOfYear(mDateTime);
int n0=mDateTime.year%4;
if(n0==0)
{
n=n;
}else if(n0==1)
{
n=n+366;
}else if(n0==2)
{
n=n+366+365;
}else if(n==3)
{
n=n+366+365+365;
}
double t =getHours(mDateTime);
double thet =2*M_PI*n/365.25;
//eot为分钟的单位
double eot=0.00020870*cos(thet*0)+0.0092869*cos(thet*1)-0.052258*cos(thet*2)-0.0013077*cos(thet*3)-0.0021867*cos(thet*4)-0.000151*cos(thet*5)
-0.12229*sin(thet*1)-0.15698*sin(thet*2)-0.0051602*sin(thet*3)-0.0029823*sin(thet*4)-0.00023463*sin(thet*5);
double ts=0;
ts=t+eot/60+(lon-120)/15;
//转为弧度。1个小时对应15°。
double w=M_PI/12*(ts-12);
return w;
}
1.3.2 Spencer算子
Spencer算子除了可以计算太阳赤纬,也提出了计算太阳时角的公式。其计算公式如下。其中θ为日角,单位为弧度。
eot=229.18[0.000075+0.001868cos(θ)-0.032077sin(θ)-0.014615cos(2θ)-0.04089sin(2θ)]
(28)
日角的计算公式如下,周期为1年,n为计日序数。
(29)
公式计算所得的eot值单位为分钟,需要转换为小时再进行下一步计算。
实现代码如下所示:
double SpencerTimeAngle(cDateTime mDateTime, double lon)
{
int n=getDaysOfYear(mDateTime);
double t =getHours(mDateTime);
double thet =2*M_PI*(n-1)/365;
double eot=229.18*(0.000075+0.001868*cos(thet)-0.032077*sin(thet)-0.014615*cos(2*thet)-0.04089*sin(2*thet));
double ts=0;
ts=t+eot/60+(lon-120)/15;
double w=M_PI/12*(ts-12);
return w;
}
1.3.3 Whillier算子
Whillier算子由Whillier提出,其中θ为日角,单位为弧度。计算所得eot单位为分钟,需要转换成小时。
eot=9.87sin(2θ)-7.53cos(θ)-1.5sin(θ)
(30)
日角的计算公式如下,周期为1年,n为计日序数。
(31)
实现代码如下:
double Whillier(cDateTime mDateTime, double lon)
{
int n=getDaysOfYear(mDateTime);
double t =getHours(mDateTime);
double thet =2*M_PI*(n-81)/364;
double eot=9.87*sin(2*thet)-7.53*cos(thet)-1.5*sin(thet);
double ts=0;
ts=t+eot/60+(lon-120)/15;
double w=M_PI/12*(ts-12);
return w;
}
1.3.4 Wloof算子
Wloof算子由Wloof提出,其中θ为日角,单位为弧度。计算所得eot单位为分钟,需要转换成小时。误差修正值计算公式如下:
eot=0.258cos(θ)-7.416sin(θ)-3.648cos(2θ)-9.228sin(2θ)
(32)
其中的日角公式如下,周期为1年,n为计日序数。
(33)
代码实现如下:
double Wloof(cDateTime mDateTime, double lon)
{
int n=getDaysOfYear(mDateTime);
double t =getHours(mDateTime);
double thet =2*M_PI*(n-1)/365.242;
double eot=0.258*cos(thet)-7.416*sin(thet)-3.648*cos(2*thet)-9.228*sin(2*thet);
double ts=0;
ts=t+eot/60+(lon-120)/15;
double w=M_PI/12*(ts-12);
return w;
}
1.3.5 Yu算子
Yu算子由Yu提出,除了可计算赤纬,可提出了计算太阳时角的公式,其中θ为日角,单位为弧度。计算所得eot单位为分钟,需要转换成小时。误差修正值计算公式如下:
eot=0.0172+0.4281cos(θ)-7.351sin(θ)-3.3495cos(2θ)-9.3619sin(2θ)
其中的日角公式如下,周期为1年,n为计日序数。
代码实现如下:
double YuTimeAngle(cDateTime mDateTime, double lon)
{
int n=getDaysOfYear(mDateTime);
double t =getHours(mDateTime);
double thet =2*M_PI*n/365;
double eot=0.0172+0.4281*cos(thet)-7.351*sin(thet)-3.3495*cos(2*thet)-9.3619*sin(2*thet);
double ts=0;
ts=t+eot/60+(lon-120)/15;
double w=M_PI/12*(ts-12);
return w;
}
1.3.6 VSOP87行星理论
关于VSOP87行星理论上文已有介绍,利用该理论计算的过程如下。
1)计算相对儒略世纪数,用T表示:
(34)
2)计算黄道与月球平轨道升交点黄经,用mw表示:
mw=125.04452-1934.136261×T+
(35)
3)计算太阳几何平黄经,用L表示:
L=280.466456+36000.76982779×T+
(36)
4)计算月球几何平黄经,用L1表示:
L1=218.3164591+481267.88134236×T-0.0013268×T2+0.0000019×T3
(37)
5)计算黄经章动,用NHJ表示:
(38)
6)计算平黄赤交角,用MB表示:
(39)
7)计算任意时刻格林尼治恒星时,并加上黄经章动修正,得到视恒星时用Q0表示,需要将Q0值转换到0~360°范围内:
Q0=280.4606183+360.98564736629×(J-2451545)+
(40)
8)计算太阳平近点角,用MSs表示:
MSs=357.52191+35999.0503×T-
(41)
9)计算太阳真黄经,用SYS表示:
SYS=L+(1.9146-0.004817×T-0.000014×T2)
(42)
10)计算太阳赤经,用RM表示:
(43)
11)计算当地太阳时角,用ω,需要将ω值转换到0~360°范围内,计算结果为度值,通常需要转换成弧度值,方便后续计算:
(44)
ω=Q0+lon-120-RM
(45)
实现上述公式的代码如下:
double VSOP87TimeAngle(cDateTime date,double lon)
{
//儒略日数
double J=date2JD(date);
//计算相对儒略世纪数
double T=(J- 2451545.0)/36525;
//黄道与月球平轨道升交点黄经
double mw=125.04452-1934.136261*T+0.0020708*pow(T,2)+pow(T,4)/450000;
//太阳几何平黄经
double L=280.466456+36000.76982779*T+0.003032028*pow(T,2)+pow(T,3)/49931-pow(T,5)/15299;
//月球几何平黄经
double L1=218.3164591+481267.88134236*T-0.0013268*pow(T,2)+0.0000019*pow(T,3);
//黄经章动
double NHJ=(-17.2/3600)*sin(mw/radeg)-(1.32/3600)*sin(2*L/radeg)-(0.23/3600)*sin(2*L1/radeg)+(0.21/3600)*sin(2*mw/radeg);
//平黄赤交角
double MB=23.4392911111-(46.815/3600)*T-(0.00059/3600)*pow(T,2)+(0.001813/3600)*pow(T,3);
//任意时刻格林尼治视恒星时,加黄经章动修正,得到视恒星时
double Q0=280.4606183+360.98564736629*(J-2451545)+0.000387933*pow(T,2)-pow(T,3)/38710000+NHJ*MB;
int n=Q0/360;
Q0=Q0-n*360;
//太阳平近点角
double MSs=357.52191+35999.0503*T-0.0001559*pow(T,2)-0.00000048*pow(T,3);
//太阳真黄经
double SYS=L+(1.9146-0.004817*T-0.000014*pow(T,2))*sin(MSs/radeg)+(0.019993-0.000101*T)*sin(2*MSs/radeg)+0.00029*sin(3*MSs/radeg);
//太阳地心赤经
double RM=radeg*atan2(cos(MB/radeg)*sin(SYS/radeg),cos(SYS/radeg));
//当地时角
double w =Q0+lon-120-RM;
int temp=w/360;
w=w-temp*360;
return w/180*M_PI;
}
2 太阳高度角及方位角的计算方法
太阳高度角和方位角,即在观察者位置观察太阳时的方位俯仰角,与当地的水平面相关,太阳高度角从地表横切面起算,取值范围为0~90°,水平角从正北方向起算,取值范围为0~360°。
计算太阳高度角时,需要考虑蒙气差的影响。
2.1 太阳高度角的计算
太阳高度角的计算公式如下,其中ψ为观察者所处地点的纬度值,δ为太阳赤纬角,e为地球椭圆扁率:
(46)
其中地球扁率公式为:
(47)
太阳高度角和方位角计算的代码如下:
cAE SunAltitudeAngle::calSunAltitudeAngle(cLocation mLocation, double hourAngle, double Dec)
{
cAE mSunAE;
double e=(earth_a-earth_b)/earth_a;
double cos_lat=cos(mLocation.dLatitude/radeg);
double cos_w=cos(hourAngle);
double cos_Dec=cos(Dec);
double sin_lat=sin(mLocation.dLatitude/radeg);
double sin_Dec=sin(Dec);
double up=cos_lat*cos_w*cos_Dec+sin_lat*sin_Dec;
double down=sqrt(1+(1/pow(1-e,2)-1)*pow(cos_Dec,2)*pow(sin_lat,2)+(pow(1-e,2)-1)*pow(cos_lat,2)*pow(sin_Dec,2));
double cos_phi=up/down;
double phi=acos(cos_phi);
double E=M_PI_2-phi;
double R0=MongolianQiDiff(1,E,16,880);//计算蒙气差,单位为角秒
E=E+(R0/3600)/radeg;
mSunAE.E=E;
double cos_A=(sin(E)*sin_lat-sin_Dec)/(cos(E)*cos_lat);
mSunAE.A=acos(cos_A);
return mSunAE;
}
2.2 太阳方位角的计算
太阳方位角的计算在计算得出高度角的基础上进行,公式如下,其中,α为太阳高度角,ψ为观察者所处纬度值,δ为太阳赤纬角。
(48)
2.3 蒙气差计算公式
蒙气差修正,即对因大气折射、温度、气压带来的误差进行修正。蒙气差的单位为角秒。在此采用李文提出的计算公式,以公式适用范围为依据,将蒙气差计算按俯仰角进行划分。下列公式输入值α为俯仰角,单位为弧度,输出值为修正值,输出为角秒。
2.3.1 蒙气差对大气折射的修正
2.3.1.1 俯仰角0~14°范围的修正
在此范围内,使用傅里叶展开法进行计算修正,修正系数采用真实记录值进行计算。计算公式如下。
(49)
实现代码如下:
double SunAltitudeAngle::Fourier(double alpha,double a[6],double b[5],double w)
{
double z=M_PI_2-alpha;
double R0=a[0]+a[1]*cos(tan(z)*w)+a[2]*cos(2*tan(z)*w)+a[3]*cos(3*tan(z)*w)+a[4]*cos(4*tan(z)*w)+a[5]*cos(5*tan(z)*w)+b[0]*sin(tan(z)*w)+b[1]*sin(2*tan(z)*w)+b[2]*sin(3*tan(z)*w)+b[3]*sin(4*tan(z)*w)+b[4]*sin(5*tan(z)*w);
return R0;
}
2.3.1.2 俯仰角15~45°范围的修正
在此范围内,采用数值拟合法进行修正,修正系数采用真实记录值进行计算,修正公式如下:
(50)
实现代码如下:
double SunAltitudeAngle::NumericalFitting(double alpha, double a[8])
{
double z=M_PI_2-alpha;
double R0=a[0]*pow(tan(z),0)+a[1]*pow(tan(z),1)+a[2]*pow(tan(z),2)+a[3]*pow(tan(z),3)+a[4]*pow(tan(z),4)+a[5]*pow(tan(z),5)+a[6]*pow(tan(z),6)+a[7]*pow(tan(z),7);
return R0;
}
2.3.1.3 俯仰角46~90°范围的修正
高俯仰范围内的修正方法较多,常见的有5种算法。
1)算法一的计算公式如下:
(51)
2)算法二的计算公式如下:
(51)
3)算法三的计算公式如下:
(52)
4)算法四的计算公式如下:
(53)
5)算法五的计算公式如下:
(54)
实现上述公式的代码如下:
if(type==1)
{
R0=60.2*tan(z);
}else if(type==2)
{
R0=(1819.08+194.89*alpha+1.47*pow(alpha,2)-0.042*pow(alpha,3))/(1+0.41*alpha+0.067*pow(alpha,2)+0.000085*pow(alpha,3));
}else if(type==3)
{
R0=1.02/tan((alpha+10.3/(alpha+5.11))*M_PI/180);
}else if(type==4)
{
R0=60.097*tan(z)+0.0109*pow(tan(z),2)-0.073*pow(tan(z),3)+0.002*pow(tan(z),4);
}else if(type==5)
{
R0=60.103*tan(z)-0.066*pow(tan(z),3)-0.00015*pow(tan(z),5);
}
2.3.2 蒙气差对温度、气压的修正
蒙气差还会受温度和湿度的影响,因此需要对蒙气差进行附加值修正。输入值为蒙气差值,单位为角秒,输出值为蒙气差修正值,单位为角秒。蒙气差修正公式如下。其中在高仰角(通常指大于45°)的情况下,大气折射对温度也会有一个影响,因此需要对温度再进行一次修正,其中μ为对温度的附加修正。
R=R0(1+μA+B)
(55)
其中:μ的修正公式如下:
(56)
低仰角时,无需对温度进行修正。蒙气差修正公式如下:
R=R0(1+A+B)
(57)
对温度的修正公式如下:
(58)
对气压的修正公式如下:
(59)
上述公式实现代码如下:
double SunAltitudeAngle::MongolianQiDiffPlus(double alpha,double R,double T,double P)
{
double R0=0;
double A=-0.00383*T/(1+0.00363*T);
double B=P/101324.72-1;
if(alpha<(45/radeg))
{
double a[6]={1.00011366,-8.95854338e-4,1.77241695e-3,-9.29720341e-5,2.00679856e-6,-1.5325798e-8};
double z=M_PI_2-alpha;
double mu=a[0]*pow(tan(z),0)+a[1]*pow(tan(z),1)+a[2]*pow(tan(z),2)+a[3]*pow(tan(z),3)+a[4]*pow(tan(z),4)+a[5]*pow(tan(z),5);
R0=R*(1+mu*A+B);
}else{
R0=R*(1+A+B);
}
return R0;
}
3 飞行器与太阳夹角的计算方法
在计算出太阳高度角和方位角以后,同时已知飞行器的方位俯仰角,此时便能计算出飞行器与太阳之间的夹角。
计算夹角有两种方法:一种是向量点乘的方法,另一种是三角函数推导的方法。
飞行器与太阳及观测点之间的相互关系如图2。F点为飞行器,S点为太阳,P点为观察点,太阳夹角即图中所示∠FPS。
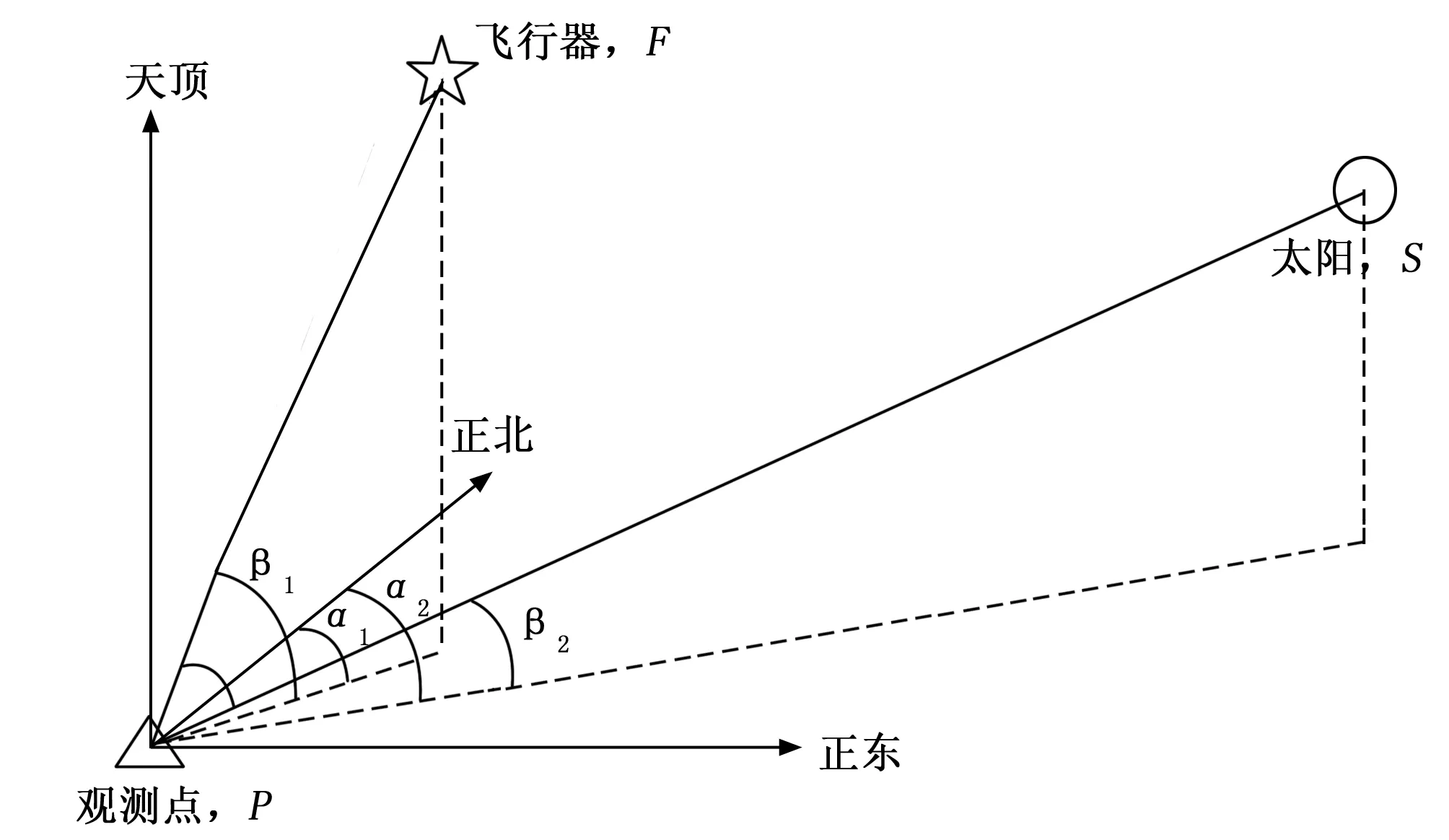
图2 太阳夹角示意图
计算时,为方便计算,取模的长度为1,α1为飞行器点的方位角,β1为飞行器的俯仰角,α2为太阳的方位角,β2为太阳的俯仰角。则F点方向可以假定一个模长为1点F′,其坐标可以表示为F′(cosβ1sinα1,cosβ1cosα1),同理,在S点方向可以假定一个模长为1的点S′,其坐标可以表示为S′(cosβ2sinα2,cosβ2cosα2)。正东方向取为X轴正方向,正北方向取为Y轴正方向。
3.1 向量点乘法
向量点乘的计算公式如下:
(60)
根据F′与S′的值,代码实现如下:
double SolarAngle::dotProduct(cAE SunAE, cAE CraftAE)
{
cXYZ Sun_XYZ;
cXYZ CraftAE_XYZ;
double alpha1=SunAE.A;
double beta1=SunAE.E;
double alpha2=CraftAE.A;
double beta2=CraftAE.E;
Sun_XYZ.X=cos(beta1)*cos(alpha1);
Sun_XYZ.Y=cos(beta1)*sin(alpha1);
Sun_XYZ.Z=sin(beta1);
CraftAE_XYZ.X=cos(beta2)*cos(alpha2);
CraftAE_XYZ.Y=cos(beta2)*sin(alpha2);
CraftAE_XYZ.Z=sin(beta2);
double thet=acos(Sun_XYZ.X*CraftAE_XYZ.X+Sun_XYZ.Y*CraftAE_XYZ.Y+Sun_XYZ.Z*CraftAE_XYZ.Z);
return thet;
}
3.2 三角函数推导
在PF与PS两条线段上,从P点出发,取一个长度为1的线段,记作F′和S′,将F′和S′相连,成一个等腰三角形,计算F′S′长度,从而求出∠F′PS′,即太阳夹角。
经推导,计算公式结果如下:
(61)
代码实现如下:
double SolarAngle::trigonometric(cAE SunAE, cAE CraftAE)
{
double alpha1=SunAE.A;
double beta1=SunAE.E;
double alpha2=CraftAE.A;
double beta2=CraftAE.E;
double thet=2*asin(sqrt(2-2*cos(beta1)*cos(beta2)*cos(alpha1-alpha2)-2*sin(beta1)*sin(beta2))/2);
return thet;
}
4 飞行器与太阳夹角的精度分析
为比较各算法的计算结果,进行精度分析。
4.1 精度分析方法
用以进行数值精度鉴定的参考数据,通常有两种来源,一是通过实际观察获取的实测记录值,另一种来源是精度更高的计算值。在本次计算赤经赤纬数值的精度鉴定中,采用第二种方法,以精度更高的计算值来作为参考值的办法。采用复杂算法SPA算法的计算值作为数据的参考值,SPA算法是综合考虑了海拔、压强、温度、倾斜度、方位角旋转、大气折射、时区、地球自转时间与地球时间之差等各方面因素的算法,其计算精度可达±0.000 3°,可以用来作为参考值对简单算法进行精度分析。
因此在对太阳夹角的数值分析时,选用SPA算法作为参考值。误差分析选用均值、方差、均方根三项指标进行分析。
飞行器飞行轨迹选用样本,按照每秒一个点,每秒在方位、俯仰方向上各新增0.000 1°,全时长为300秒设计。飞行时间设定为2018年8月8日上午10点整。起飞地点设置为东经102.241 897 39,北纬27.902 341 42。
数据样本为全飞行轨迹中,每个点的太阳夹角与参考值的差值。
均值即将样本值求均值。公式如下:
(62)
方差为将样本值与样本的均值相减,分别求平方后求和,再将平方和求均值。
(63)
均方根,将所有样本值分别求平方,再求平方和以后求平方和的均值,最后开平方。
(64)
分析对象为:9种太阳赤纬角算法,6种太阳时间算法。
4.2 精度分析结果
4.2.1 均值分析结果
均值分析结果如表1所示。
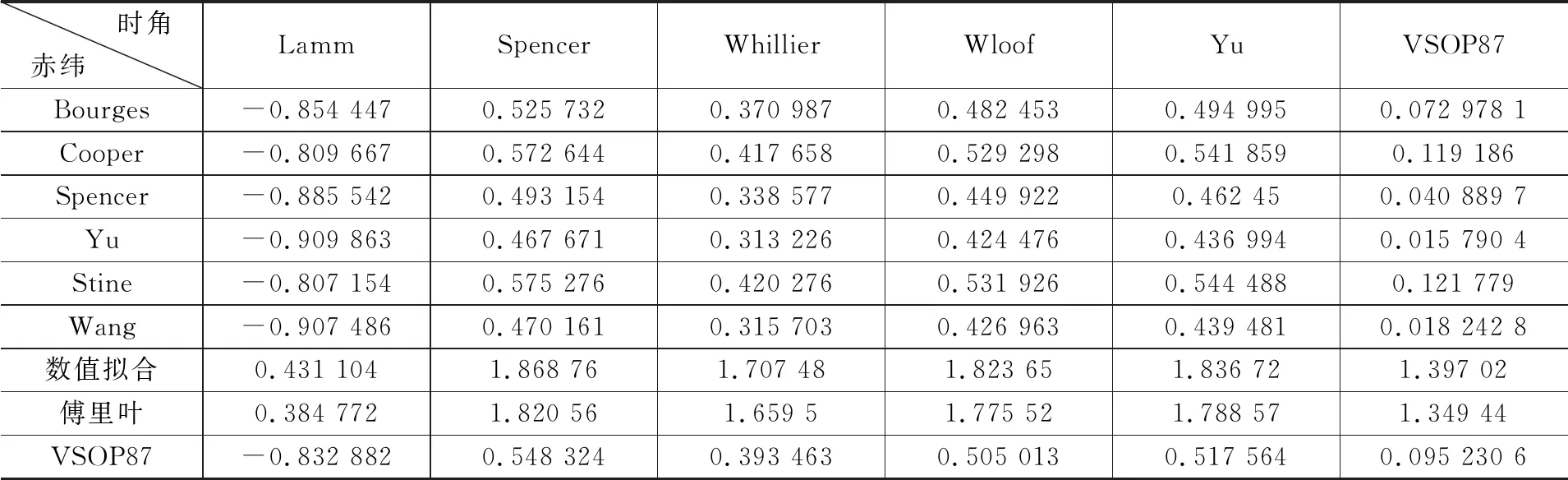
表1 均值计算结果
图3为折线图形式。横坐标为赤纬算子,每一条折现代表一种时角算法。
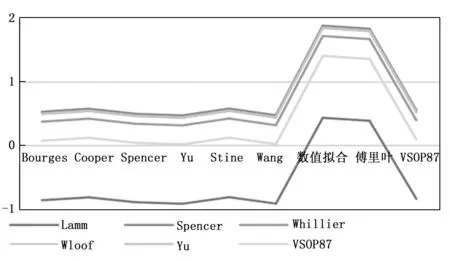
图3 均值折线图
均值能反映统计样本的大致的平均水准,均值越小,说明样本值整体越小。从表1均值计算结果分析可得以下结论。
1)不同的赤纬角算子下,VSOP87的时角计算结果偏差最小。
2)不同的时角算子下,Wang算法的赤纬角计算结果偏差最小。
4.2.2 方差分析结果
方差分析结果如表2所示。
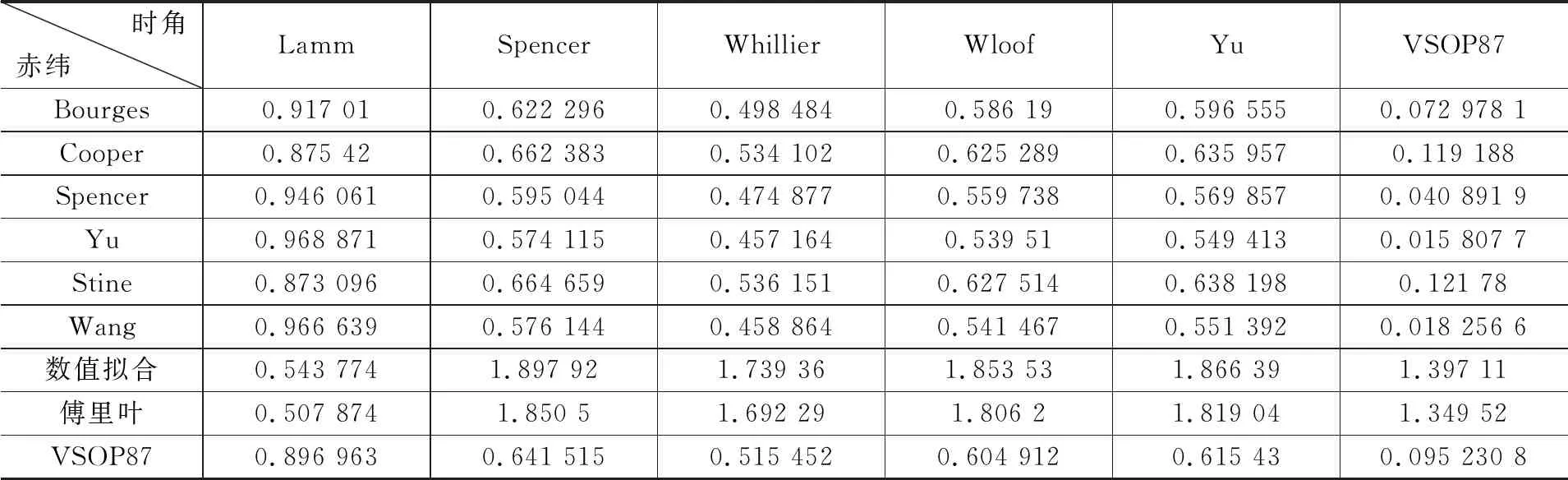
表2 方差计算结果
图4为折线图形式。横坐标为赤纬算子,每一条折现代表一种时角算法。
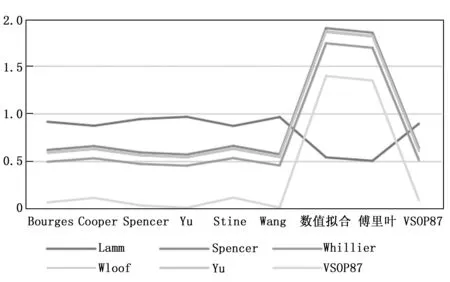
图4 方差折线图
方差分析反映的是自变量对数值的影响。即对于均值的偏离度的一个分析,即数值的稳定程度。数值越小,说明数值越稳定,起伏越小。
1)在不同的赤纬角算子,VSOP87的时角计算结果波动最小。
2)在不同的时角算子下,Wang算子的赤纬角计算结果波动最小。
4.2.3 均方根分析结果
均方根分析结果如表3所示。
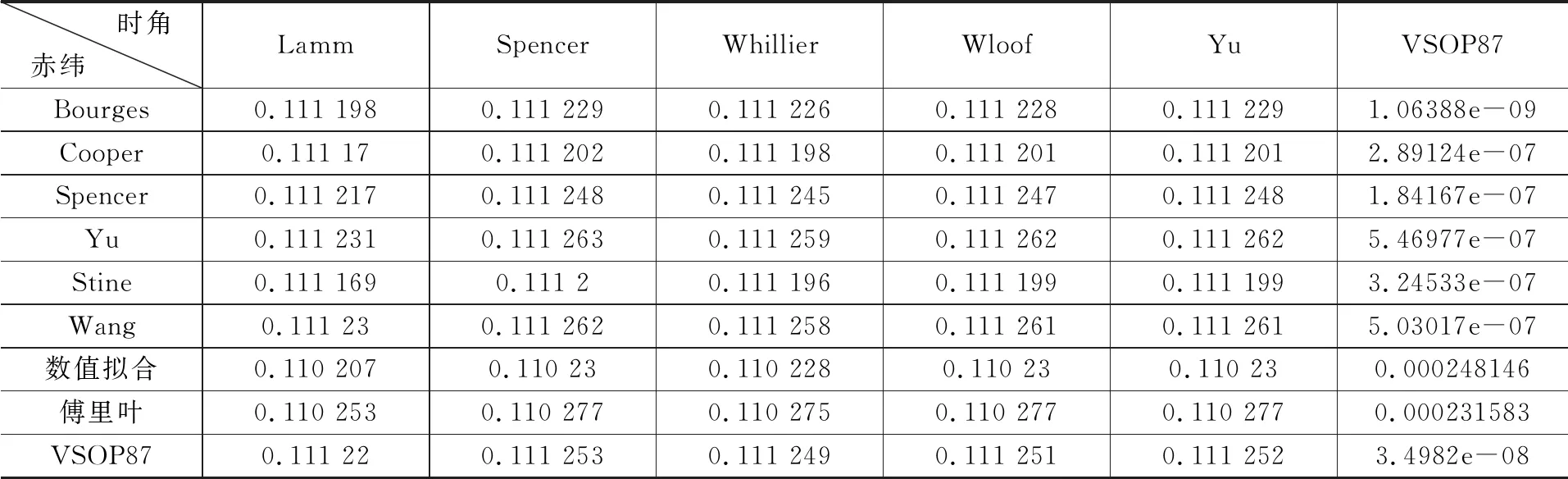
表3 均方根计算结果
图5为折线图形式。横坐标为赤纬算子,每一条折现代表一种时角算法。

图5 均方根折线图
均方根和均值一起分析,反映了样本的一致性情况。均方根和均值越接近,说明样本数据一致性越好。
1)在不同的赤纬角算子下,VSOP87的时角一致性最好。
2)在不同的时角算子下,Wang算子的赤纬角一致性最好。
5 结束语
本次实验实现了从计算太阳赤纬角和太阳时角,到计算太阳高度角和方位角,最后计算得到飞行器与太阳夹角。在C++环境中,实现了9种太阳赤纬角,6种太阳时角,2种太阳夹角以及相应的蒙气差修正等过程的计算,并分析了9种太阳赤纬角算法,以及6种太阳时角算法对太阳夹角的影响,结果表明,所有简单算法中,VSOP87的时角算子与Wang赤纬角算子的计算结果最为真实可靠。在日常使用的简单计算中,推荐使用Wang赤纬角算子及VSOP87时角算子计算太阳夹角。
