基于深度学习的知识追踪研究综述

王丹萍，王 忠，梁宏涛

(青岛科技大学 信息科学技术学院，山东 青岛 266061)

0 引言

随着人工智能、大数据、智能教学平台(ITS,intelligent tutoring system)等信息技术的不断发展无形中推动了教育形式由传统向新型模式的转变。《中国教育现代化2035》)[1]提出，高校需探求新的教学模式，促进以个性化学习为基础的教学，以推动人工智能在教育方面的应用。虽说人工智能的发展为学生自主学习提供了可能，但也带来了诸多挑战，例如，在线学习平台学生的数量远超于教师数量，教师难以提供学生个性化教学。因此，基于学生历史学习数据，如何利用科学有效的方法针对学生的学习状态进行准确分析与预测，已成为目前智慧教育领域中亟待解决的重要课题。

而解决个性化教学的关键是知识追踪(KT,knowledge tracing)[2]，知识追踪旨在创建学生的知识状态与认知结构随时间变化的模型，将学生的历史学习记录作为模型的输入，评估学习者的知识水平，即掌握知识的程度跟随时间变化的过程，以此来预测学生在未来学习中的作答表现，实现个性化学习辅导[3]。

通过查阅知识追踪领域综述文献可知，业界研究者们根据知识追踪领域的数据信息特点、变量的表示形式、建模方法针对知识跟踪模型展开研究。Liang等[4]总结了知识追踪模型在智慧教育领域的改进模型及其应用。Li等[5]从学习者、历史学习数据、知识点等详细阐述了知识追踪在教育界的应用研究。其中值得提出的是Zeng等[6]探究了在智慧教育视域下的知识追踪的现状及发展趋势，总结了学生与学习资源的交互过程。Zhang等[7]探讨了知识追踪领域研究进展，Wei等[8]总结了知识追踪领域模型的优缺点，未对深度学习改进模型进行详细介绍，通过知识追踪领域的研究综述来看还有很多内容亟待解决。

通过查阅、检索计算机领域顶级期刊，阅读、梳理、总结知识追踪模型，从模型的原理、不足、改进、应用对教育领域的知识追踪进行比较、分析、应用、总结和展望。简要介绍了传统知识追踪模型的原理、特点以及不足。全面梳理了基于深度学习的知识追踪及其改进模型，分别从可解释性问题、缺少学习特征、记忆增强网络、图神经网络、引入注意力机制的改进模型详细介绍。整理了知识追踪领域的公开数据集，评价指标及模型性能对比分析，探讨了知识追踪在智慧教学领域的实际应用，总结了该领域目前的研究现状和未来的研究方向。

1 传统知识追踪模型

在智慧教学领域，依据数据和建模形式不同，知识追踪模型分为机器学习和深度学习方法，机器学习方法中最具代表性的是基于隐马尔可夫模型[9](HMM,hidden markov model)的贝叶斯知识追踪模型[10](BKT,bayesian knowledge tracing)。1995年，Corbett等[11]首次提出将BKT引入到智能教学中。BKT的核心原理是基于时间序列的隐马尔可夫概率模型，建立学生对于知识集合的认知状态随时间变化的模型，追踪和分析学生在下一时刻掌握知识点的概率，模型图如图1所示。

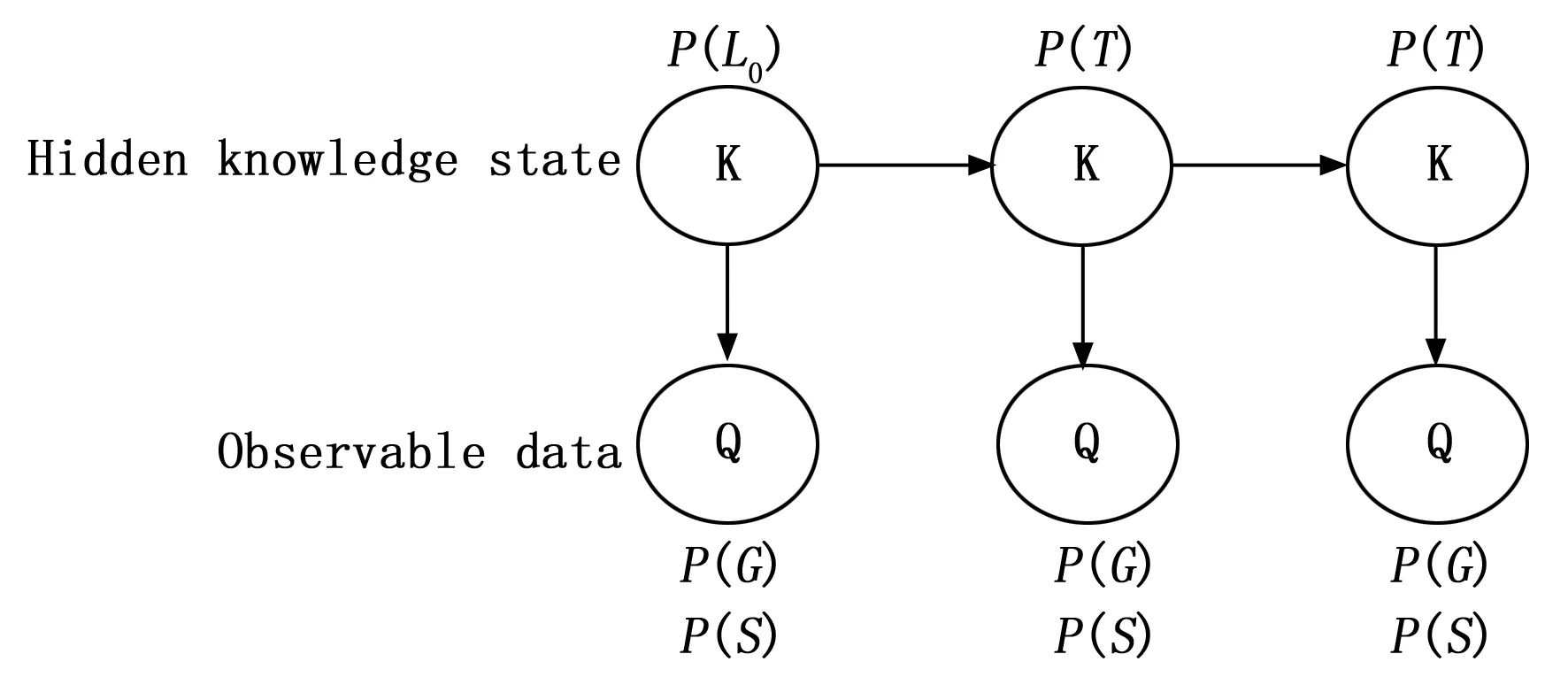
图1 BKT模型原理图

在传统BKT模型中，学生的知识掌握概率主要受到以下这四个参数的影响：P(L)是学习者在学习前对知识掌握的概率；P(T)指学生掌握知识的情况由“未掌握”到“掌握”的概率；P(T)指学生掌握知识的情况由“未掌握”到“掌握”的转移概率；P(G)指学生在未掌握知识的情况下正确作答习题的概率，称为猜测概率；P(S)指学生在掌握知识的情况下错误作答习题的概率，称为失误概率。一般来说，BKT模型是基于学生的作答信息追踪其认知状态，当P(L)≥0.95时,则认为学生对知识点已掌握，值得关注的是，BKT模型基于如下三点假设。

1)假设所有学生具备相同的学习环境和学习背景，并且转移概率P(T)在不同时刻保持不变。

2)假设每个题目之间不具备相关性，各个题目之间相互独立。

假设学生不会遗忘已学知识点，即学生掌握知识的状态仅能由“未掌握状态”转移到“掌握状态”，不能反向转移。

3)BKT模型预测结果虽说具有统计学解释意义，但应用于实际教学仍存在较多局限性。随后，诸多研究学者做了一系列深入和丰富的研究，从不同角度对BKT模型进行改进与扩展。Hawkins等[12]基于学生作答的习题具有相似性和关联性，提出了贝叶斯知识追踪相同模板模型(BKT-ST,bayesian knowledge tracing-same tamplate)模型。Qiu等[13]提出KT-Forget模型和KT-Slip模型，尝试对时间因素进行建模，新模型考虑参数“忘记”和“滑动”参数，在残差和AUC都得到了改进和提升。Agarwal等[14]提出多状态贝叶斯知识跟踪模型(MS-BKT,multistate-Bayesian knowledge tracing)解决经典知识追踪模型中的学习率不变且仅有两种知识状态，此模型将知识状态从“未学习”、“已学习”扩展到21种状态，多个状态的添加能更精确地评估学生的学习状态，提升了模型的性能。

诸多研究学者在贝叶斯知识追踪的基础上提出了扩展模型，BKT改进模型虽说取得了一定成效，但是BKT模型的假设具备先天局限性，变量和KC之间无法做到以一一对应，且模型本身在处理数据过程中会丢失重要信息，无法准确模拟学生的知识状态,因此，BKT模型在实际教学过程中难以大范围推进。

2 基于深度学习的知识追踪

由于BKT模型本身的局限性，无法准确追踪学生的作答表现。而近年来深度学习以其强大的特征提取能力，且无需人工标记数据信息，引起了研究者的广泛关注，2015年由Piech等[15]首次将深度学习应用于知识追踪领域，基于循环神经网络(RNN,recurrent neural network)[16]，提出一个经典模型，称为基于深度学习[17]的知识追踪模型(DKT,deep learning based knowledge tracing)。

2.1 DKT模型原理

DKT模型结构如图2所示。将循环神经网络RNN模型应用于知识跟踪中，DKT模型分为输入层、隐藏层、输出层[18]，输入层为学习者的学习表现，即历史学习记录{x1,x2,…,xt}，通过压缩感知机[19]或one-hot编码将其转换成向量形式输入到模型中。隐藏层可看作模型的记忆单元，存储着学生的历史学习记录{h1,h2,…,ht}称为学生的知识状态，通过一个sigmoid[20]激活线性层，输出未来学生的作答表现{y1,y2,…,yt}，表示正确作答习题的预测概率。

图2 DKT模型原理图

由图2可知，每个时刻的隐藏信息仅单向传递，因此当前时刻的隐藏状态仅由上一时刻的隐藏信息和当前时刻的输入信息决定。在DKT模型中所涉及的公式如式(1)、(2)所示，其中，Whx、Wyh分别为输入和输出权重矩阵，Whh是递归权重矩阵，bh和by分别为隐藏层偏置和输出层偏置。

ht=tanh(Whxxt+Whhht-1+bh)

(1)

yt=σ(Wyhht+by)

(2)

DKT模型的优化目标函数是小批次次梯度随机下降法[21](SGDM,stochastic gradient descent on minnbatches)，公式如式(3)所示:

(3)

其中:LBCE为交叉熵损失函数，δ(qt+1)称为学生在t+1时刻的作答习题表现的One-hot编码向量。qt+1为t+1时刻作答的习题标签，at+1为回答习题情况的标签。

2.2 DKT改进模型

基于深度学习的DKT模型已经解决了传统BKT模型的大多数问题，但由于深度学习模型的输入和输出机制不具备可解释性，缺少学习特征等极大地限制了知识追踪模型在实际教学方面的应用[22]，因此，众多研究学者针对深度学习的知识追踪模型进行改进与扩展，具体分类如图3所示。

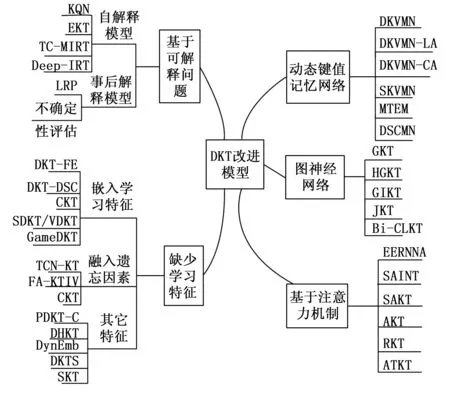
图3 DKT改进模型思维导图

2.2.1 可解释性问题的改进

1)自解释模型。为更好地解决知识交互等可解释性问题，Lee等[23]提出了一种新的知识查询网络模型(KQN,knowledge query network)，利用神经网络将学生的学习活动编码为知识状态和技能向量，将技能向量之间的余弦和欧氏距离[24]与相应技能的优势比联系起来，使KQN具有可解释性和直观性。Yeung等[25]提出(Deep-IRT,deep-item response theory)模型，通过DKVMN模型处理学生的历史学习规则，既保留了深度学习知识追踪模型的性能，同时能够预测知识的难易程度和学生的知识状态随时间的变化，使模型预测的过程具备可解释性。Su等[26]提出了新的框架—时间-概念增强深度多维项目反应理论(TC-MIRT,time concept-multidimensional item response theory)将历史学习记录集成到一个改进的递归神经网络中，构建两个时间增强组件，使模型具备可解释参数的能力。

2)事后解释模型。事后解释(post-hoc interpretable)方法是解决模型不可解释性的有效方法，意旨模型预测结束后，通过解释方法构造解释模型，解释学习模型的预测过程、预测依据，事后解释方法既能解决模型的解释过程、又能提高模型预测性能。在KT领域，主要有两种方法，分为层关联传播(LRP,layer-wise relevance)和不确定性评估。Lu等[27]提出分层相关性传播方法，利用反向传播将相关性分值传输到输入层，计算反向传播相关性。Hu等[28]首次将评估不确定性引入深度知识追踪，通过为每个预测提供不确定分数，首次实验表明，仅使用蒙特卡罗效果不明显，接着引入正则化损失函数，将敏感的不确定性纳入深度知识跟踪，以此来缓解预测学生知识状态过程中的不透明性。

2.2.2 缺少学习特征的改进

虽然DKT及其变体模型是目前应用于知识追踪领域最具成效的方法，但由于DKT模型的输入仅是one-hot编码，忽略了学习过程中其余重要的特征信息，如：学生作答题目的次数、思考时间、习题内容等，因此DKT模型未能大范围进行个性化教学。

1)嵌入学习过程特征。Yang等[29]提出了一种人工对特征进行预处理的方法，即根据学生的内部特征将其离散化，使用基于树的分类器(CART)将学生的额外特征信息(学习者的响应时间、提示请求和尝试作答次数)进行预处理，通过最小化交叉熵学习分类规则，学习特征经过CART融合处理后作为长短期记忆网络(LSTM,long short-term memory)的输入，输出为学生在异构特征下正确回答习题的预测结果。

Zhang等[30]利用特征工程的方法将学习特征离散化，把离散后的特征(学生作答的时间、提示请求和尝试作答次数)，通过自动编码网络层，将输入信息转化成低维特征向量,减少模型训练的时间和资源。Minn等[31]提出基于动态学生分类的深度知识跟踪模型(DKT-DSC,deep knowledge tracing dynamic student classification)，融合k-means聚类，在每个时刻估计学生的学习能力，并根据学生学习能力的相似性将学生分配小组，学习能力相似，则为同一组，根据学生所分组追踪认知状态。

DKT模型仅将作答习题的结果作为模型的输入，忽略了提问环节能反映学生的思维过程，Chan等[32]提出基于点击流的(CKT,clickstream knowledge tracing)模型，通过对学生作答习题时的点击流活动建模来扩充一个基本的KT模型，并将与不使用点击流数据的基准KT模型进行比较，实验数据表明，合并点击流数据可以提高模型的性能。

由于学习过程包含着许多不能直接观察到的潜在事件，如片面理解、犯错等，Ruan等[33]首先提出序列深度知识跟踪(SDKT,sequence-to-sequence deep knowledge tracing)模型，通过编码器-解码器结构将学生的历史学习记录和未来的作答表现区分开。编码器用于对学习历史记录进行编码，解码器用于预测学生的未来表现。接着Ruan等人提出变分深度知识追踪(VDKT,variational deep knowledge tracing)模型，称为潜变量DKT模型，通过潜变量将随机性融入DKT模型中。Hooshyar等[34]提出GameDKT模型，模拟学生在游戏过程中的知识状态，利用交叉验证预测学生在未来时刻的表现。

2)融入遗忘因素。Wang等[35]提出个人基础与遗忘融合的时间卷积知识追踪模型(TCN-KT,temporal convolutional network knowledge tracing)融合了学生遗忘行为，利用RNN计算得出学生先验基础，接着利用TCN时间卷积网络预测作答下一习题的正确率。Nagatani等[36]基于学习过程中的遗忘信息，提出融合遗忘信息的知识追踪模型，考虑了学生的整个学习互动过程，并纳入了多种类型的信息来表示复杂的遗忘行为。例如，学生回答相同习题的时间间隔、相邻习题的时间间隔、历史作答习题的次数。添加遗忘特征的模型如图4所示。

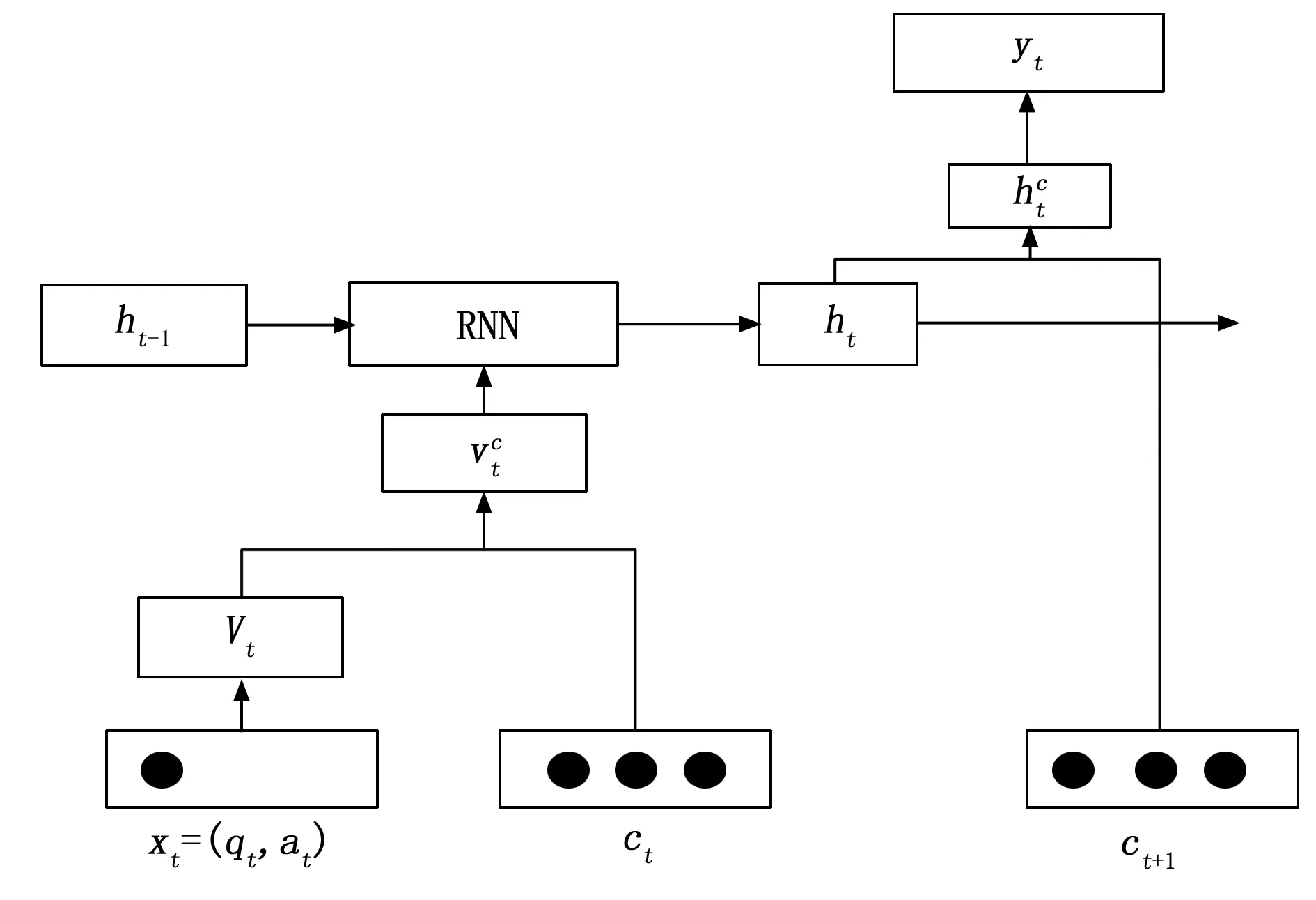
图4 添加遗忘特征模型图

Gan等[37]基于学生的知识状态是随着时间不断变化的，提出领域感知的知识跟踪机(FA-KTM,field-aware knowledge tracing machine)，融合了学生的学习行为，即(遗忘和学习的动态过程)和适应性项目难度，相较于DKT模型性能表现良好。Yang等[38]基于遗忘曲线理论提出了一种更新门来适应融合特征的卷积知识跟踪模型(CKT,convloutional knowledge tracing)，利用三维卷积增强了近期作答习题的短期效应，利用LSTM对融合后的特征进行处理，通过实验数据证明优于最先进的模型，模型图如图5所示。

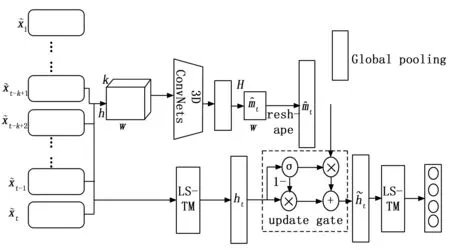
图5 卷积知识跟踪模型

3)其它特征。由于传统DKT模型存在两大主要问题，其一是模型预测时无法输入重构信息，即使学生作答习题表现较好，但预测的结果准确度降低；其二是时间间隔对于预测结果的影响，存在突然的波动和下降。为了解决这些问题，Yeung等[39]在损失函数中添加了重构和波性对应的正则化项。

Chen等[40]考虑到学生练习数据的稀疏性是影响知识跟踪预测精度的重要因素，提出了名为先决条件驱动的带约束建模的深度知识跟踪(PDKT-C,prerequisite-dreven deep knowledge tracing)，模型融合了前提条件约束，将教学概念之间的关系与知识结构信息同时融入了知识跟踪模型中。

Wang等[41]为了更好区分习题和概念的关系，提出了一种深度层次知识跟踪(DHKT,deep hierarchical knowledge tracing)模型，通过计算嵌入内积的铰链损失(hinge loss)以及利用习题和知识成分之间的层次信息，将得到的结果作为神经网络的输入，评估学生的学习作答表现，模型预测的结果取决于当前时刻作答习题和知识状态。

Xu等[42]提出了一种新的知识追踪方法DynEmb框架，该方法结合了矩阵分解技术和最新进展的递归神经网络(rnn)，该方法无需手工标记知识标签信息，通过矩阵分解和技能标签构造问题的嵌入，将题目和知识信息融合，通过实验评估表明具备较好的鲁棒性。

Wang等[43]利用侧关系改进知识跟踪，设计了一个新的框架(DKTS,deep knowledge tracing side)，将问题的边关系纳入知识追踪，捕获习题的顺序依赖和内在关系，以跟踪学生的知识状态，在真实教育数据上的实验结果验证了所提框架的有效性。

Tong等[44]提出一种基于结构的知识追踪(SKT,structure knowledge tracing)框架，基于知识结构中的多重关系对概念间的影响传播进行建模，对于无向关系(相似关系)，采用同步传播方法，影响在相邻概念之间双向传播；对于有向关系(前提关系)，采用局部传播方法，其影响只能单向地从前任传播到后续，同时，利用门控函数更新概念在时间和空间上的状态。Pu等[45]将作答时间信息和习题的结构信息作为输入信息加入到Transformer结构中，增加时间特性来增强预测学生知识状态的准确度。

2.2.3 动态键值记忆网络模型

虽然DKT模型及其变体在追踪学生的知识状态取得了一定成效，但也存在一定的缺陷，例如，LSTM[46]通过输入门获取短期记忆(即学生的近期历史学习记录)，遗忘门保留部分长期记忆，但是学习过程中的其它影响因素保留在隐藏单元中，当学习记录数量足够多时，模型则很难准确预测学生的知识状态，因此记忆增强神经网络(MANN,memory augmented neural network)[47]是解决上述局限的创新型方法。记忆增强神经网络在循环神经网络基础上添加了记忆矩阵，能够将学习过程中隐藏的状态作为输入，提高了知识追踪模型的性能。

香港中文大学施行建教授受到MANN模型的启发，提出动态关键值记忆网络(DKVMN,dynamic key-value memory networks)[48]，此模型在内存中使用键值对，对不可变的关键组件进行输入，通过读取和写入值矩阵追踪学生的知识状态，直接输出学生对每个概念的掌握程度。

DKVMN模型如图6所示，由三部分组成，左下部分表示相应权重计算的过程，即通过注意力机制计算习题和知识成分之间的权重，上部分代表读取过程，即依据学生当前作答习题的难易程度和掌握知识状态的水平预测学习表现，右部分表示写入过程，即作答习题记录利用擦除加法更新知识状态，DKVMN模型的步骤如下所示。

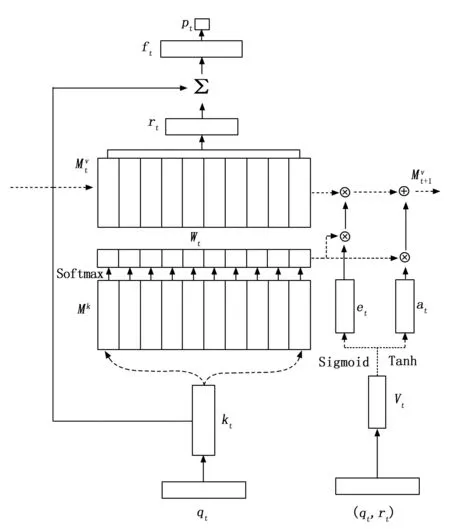
图6 DKVMN模型图

1)输入向量qt与嵌入矩阵A得到连续向量kt，Mk矩阵中每一列存储着一个知识成分，矩阵Mv中存储着知识状态，在t时刻，将kt与知识成分(即Mk的每一列)做内积，通过Softmax函数激活，进一步计算相关权重，即注意力权重Wt，公式如式(4)所示:

Wt=Softmax(ktMk(i))

(4)

2)根据注意力权重Wt与矩阵Mv进行求和得到rt，即学生对qt的掌握程度，公式如式(5)所示:

(5)

3)由于每个习题难易程度不同，将习题的嵌入向量kt与对习题的掌握程度rt连接起来，通过全连接层和Tanh激活函数，得到学生掌握知识的程度和之前练习的难度即ft，计算公式如式(6)所示:

(6)

4)通过Sigmoid激活全连接层预测学生的作答表现yt，公式如式(7)所示:

(7)

由于DKVMN模型忽略了习题信息和学生的行为特征，Ai等[49]提出了概念感知的深层知识追踪模型(DKVMN-CA,dynamic key-value memory networks concept-aware)，首次将深度强化学习应用于个性化数学练习推荐系统，在DKVMN模型的基础上，明确考虑了练习——概念映射关系，当学生作答习题结束后，作答结果和练习时间将用于更新知识状态。

Sun等[50]在DKVMN模型基础上，提出一种结合行为特征与学习能力的知识跟踪算法(DKVMN-LA,dynamic key-value memory networks learning ability)，DKVMN-LA算法将学生的历史学习记录分段，定义和计算在每个分段中的学习能力，并动态地将学生分为三个不同的组，结合学习能力特征改进了DKVMN，在学习过程中利用学生行为特征获取信息，提高了模型的预测。

Abdelrahman等[51]提出了(SKVMN,sequential key-value memory networks)模型，通过增加键值存储器来增强每个时刻知识状态的表示能力，并且能获取序列中不同时刻的知识状态之间的依赖关系，其次在模型中增加了带有跳数的LSTM，利用三角隶属度函数探索习题之间的顺序依赖关系；最后通过摘要向量作为练习过程的输入改进了DKVMN的写入过程，以便更好地表示存储在键值内存中的知识状态。

Chaudhry等[52]提出一个多任务记忆增强深度学习模型(MTEM,multi-task memory enhances deep learning)来联合预测线索获取和知识跟踪任务，通过实验证明，此模型优于基线线索获取预测模型。Minn等[53]提出一种新的基于记忆网络的动态学生分类(DSCMN,dynamic student classification on memory networks,)模型，通过捕捉学生每个时间间隔以及长期学习过程中的学习能力来提高模型的预测精度。

2.2.4 图神经网络模型

从知识追踪领域的数据结构特点来看，可以将课程结构化一个图，但DKT模型未考虑这种潜在的图结构，Nakagawa等[54]将图神经网络(GNN,graph neural network)首次应用于知识追踪领域，提出了基于GNN的图知识追踪模型(GKT,graph-based knowledge tracing)，如图7所示，将知识结构转化为一个图，节点对应概念，边对应之间的关系为E，将知识追踪任务看作时间序列节点级分类问题，GKT模型的具体计算步骤如下。

1)聚合；模型聚合作答的概念i及其相邻概念j∈Ni的隐藏状态和嵌入。

(8)

其中:xt∈{0,1}2N是一个输入向量，表示在t时间步时作答习题的正确性，Ex∈R2N*e是嵌入概念索引和答案响应的矩阵，Ec∈RN*e是嵌入概念索引的矩阵，Ec(k)代表Ec的第k行，e为嵌入大小。

1)更新；依据聚合特征和知识图结构更新隐藏状态。

(9)

(10)

(11)

由式(9)～(11)所示，fself表示多层感知器(MLP)，gea表示擦加门，ggru是门选循环单元(GRU)门，fneighbor是一个向相邻节点传播的函数。

2)预测；输出学生在下一时刻作答习题表现为正确的预测概率。

(12)

其中:Wout是所有节点通用的权重矩阵，bk是节点k的偏差项，σ是Sigmoid函数，训练该模型以使观测值的负对数似然(NLL)最小化。

由于知识追踪模型未能全面挖掘历史学习过程中其余丰富的信息，Tong等[55]提出了一种层级图知识追踪框架(HGKT,hierarchical exercise graph for knowledge tracing)来探索练习记录之间潜在的层级关系，引入问题图式的概念来构建一个分层的练习图，该框架充分利用了分层习题图和注意序列模型的优势，增强了知识追踪能力。

Yang等[56]提出了一种基于图的知识跟踪交互模型(GIKT,graph interaction knowledge tracing)，利用图卷积网络通过嵌入传播实质上合并了问题-技能相关性，此外，GIKT将学生对习题的掌握程度概括为当前掌握习题的状态、历史作答记录、目标问题、以及相关技能。Song等[57]基于“练习-概念”关系和多热点嵌入缺乏可解释性提出联合图卷积网络的深度知识追踪(joint knowledge tracing，JKT)，通过对原始数据和“练习-概念”的原始关系进行深度重构，分别构建了“练习-练习”和“概念-概念”的多维关系，并构建了影响子图。

由于将图引入知识追踪模型中，会过分关注节点细节，却不关注最高层信息，Song等[58]提出了一种基于双图对比学习的知识追踪(Bi-CLKT,bi-contrastive learning knowledge tracing)，设计了“练习到练习”(E2E)关系子图两层对比学习方案，涉及到子图的节点级别对比学习以获得练习的区别表示以及图级对比学习以获得概念的区别表示，实验表明，优于其他基线模型。

2.2.5 基于注意力机制

Su等[59]基于注意力机制[60]首次提出了新的训练增强递归神经网络框架(EERNNA,exercise-enhanced recurrent netural network)，模型图如图7所示，利用学生的历史训练纪录和习题预测成绩，设计了双向LSTM，从习题中提取练习语义表示，在大规模真实数据上的大量实验证明了EERNNA框架的有效性，且能很好地解决冷启动问题。

图7 EERNNA 模型图

为解决数据稀疏的问题，Pandey等[61]提出自我注意知识追踪(SAKT,self -attention knowledge tracing)，从学生历史学习记录提取出知识成分，并进行追踪预测学生的作答表现。Ghosh等[62]提出一种专注知识追踪(AKT,attentive knowledge tracing)框架，利用一种新颖的单调注意力机制，将历史作答记录、评估问题的未来反应与可解释性模型结合，注意力权重用指数衰减和上下文感知的相对距离度量进行计算。对概念和问题嵌入进行正则化，捕捉相同概念习题之间的学习者个体差异。

尽管应用于知识追踪的注意机制有优势，但同样存在局限性，以往模型的注意层太浅，无法捕捉到不同习题和认知状态存在的复杂关系。因此Choi等[63]提出一个基于变压器的分离自注意知识跟踪模型(SAINT,self-attentive neural knowledge tracing)，SAINT由一个编码器和一个解码器组成，它们是由几个相同层组成的堆栈，由多头自我注意和点式前馈网络组成，特别的是，解码器层由两个多头注意力层组成，模型图如图8所示。

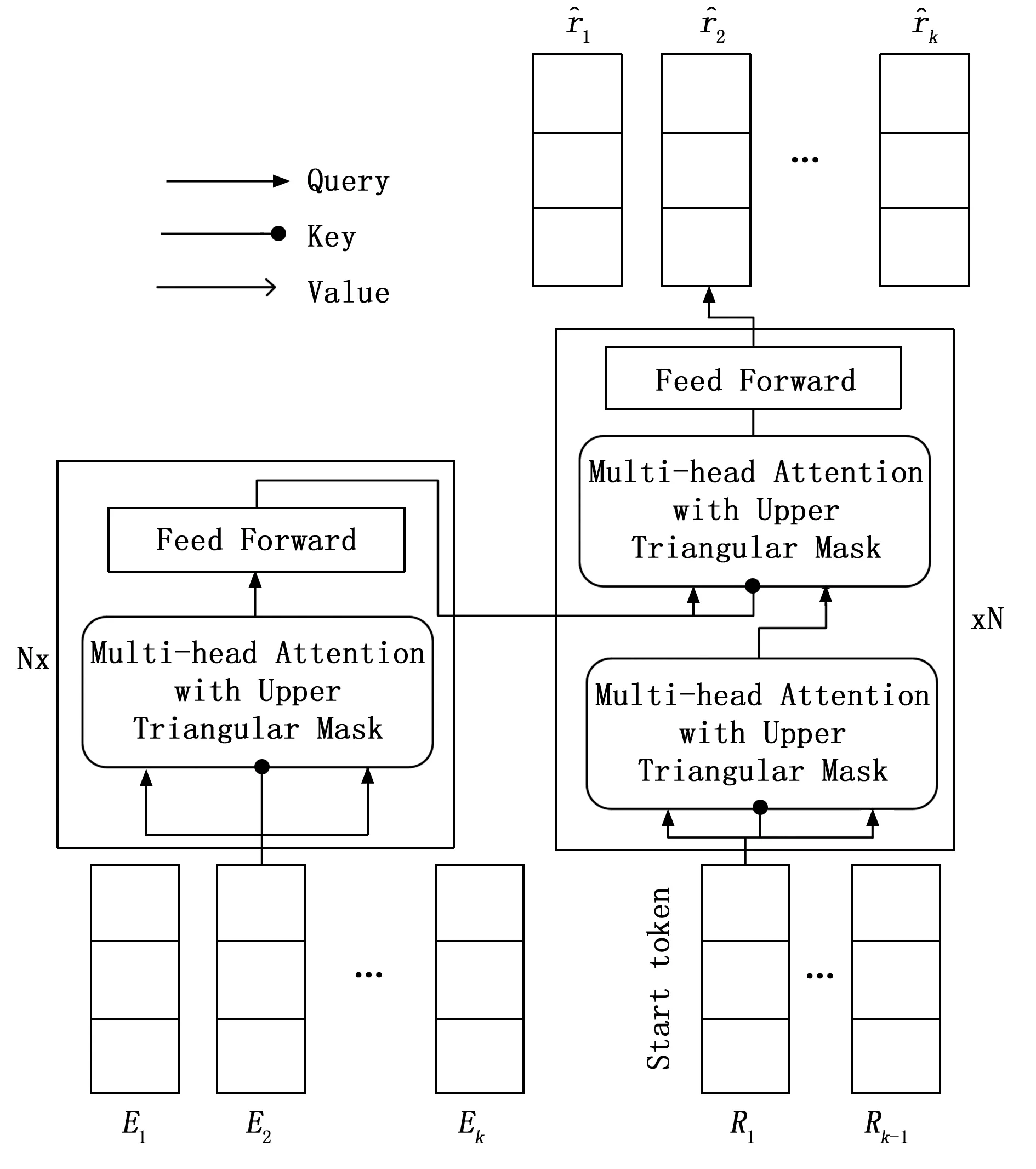
图8 SAINT 模型图

Pandy等[64]提出了一种新的感知知识追踪自注意模型(RKT,relation knowledge tracing)，添加了一个含有上下文信息的关系感知的自我注意力层，整合了习题关系信息和学生的成绩数据，并通过建立指数衰减的核函数集成了遗忘行为信息。Guo等[65]提出了一种基于对抗训练AT的KT方法(ATKT,adversarial training knowledge tracing)，首先构造了对抗摄动，并添加至原始的交互嵌入上作为对抗示例。紧接着为了更好地实现AT，Guo等提出高效的注意力-lstm模型作为KT的骨干，自适应地结合历史学习状态隐藏的信息。

综上所述，基于深度学习的知识追踪模型稳固了知识追踪在智慧教学领域的基础，结合深度学习的优势与智慧教学的现状，采用RNN模拟学生的认知状态以及预测学习表现。但传统的基于深度学习的知识追踪模型具有局限性，诸多研究学者从可解释性、缺少学习特征、动态键值记忆网络、图神经网络、引入注意力机制等方面进行模型改进。

3 模型对比分析

3.1 数据集介绍

本小节介绍在知识追踪领域中公开的10类数据集，经过整理与统计其数据集的详细信息和下载链接如表1所示，供研究者可根据所研究内容自行选择合适的数据集。

表1 数据集介绍及其下载链接

3.2 评估指标

知识追踪领域一般从分类和回归两个方面评估模型的性能，主要分为以下几种：均方根误差(RMSE,root mean square error)、代表真实值与预测值之间的差值，均方根值越低，则模型准确度越高，预测能力越好；平均绝对误差(MAE,mean absolute error)、预测准测度(ACC)，其值越高则准确率越高；ROC曲线下的面积(AUC,arer under the roc curve)，其值越高，模型的性能越好。

具体的计算公式如表2所示，其中，right代表习题预测正确的个数，N，n表示作答习题个数，h(x(i))代表第i个习题的预测分值，y(i)表示真实分值。在知识追踪领域中，诸多研究者选取AUC作为模型的评价指标，模型提供了一个评价标准，AUC的得分为0.5表示预测值和猜测值相同，AUC的值越高，则模型性能越好。

表2 评估指标及其公式

3.3 模型性能对比

表3整理了在知识追踪领域测试的模型性能表现(以最常用的AUC指标为基准)，表中数据选取原则为至少在4个数据集上做过实验，数据均来源于模型最初提出的论文，取AUC的最大值，BKT为最基础模型作为参考，根据实际意义得知，在不同的数据集上模型性能均不同，往往受到超参数的影响，因此，表中数据的参考价值大于实际意义。

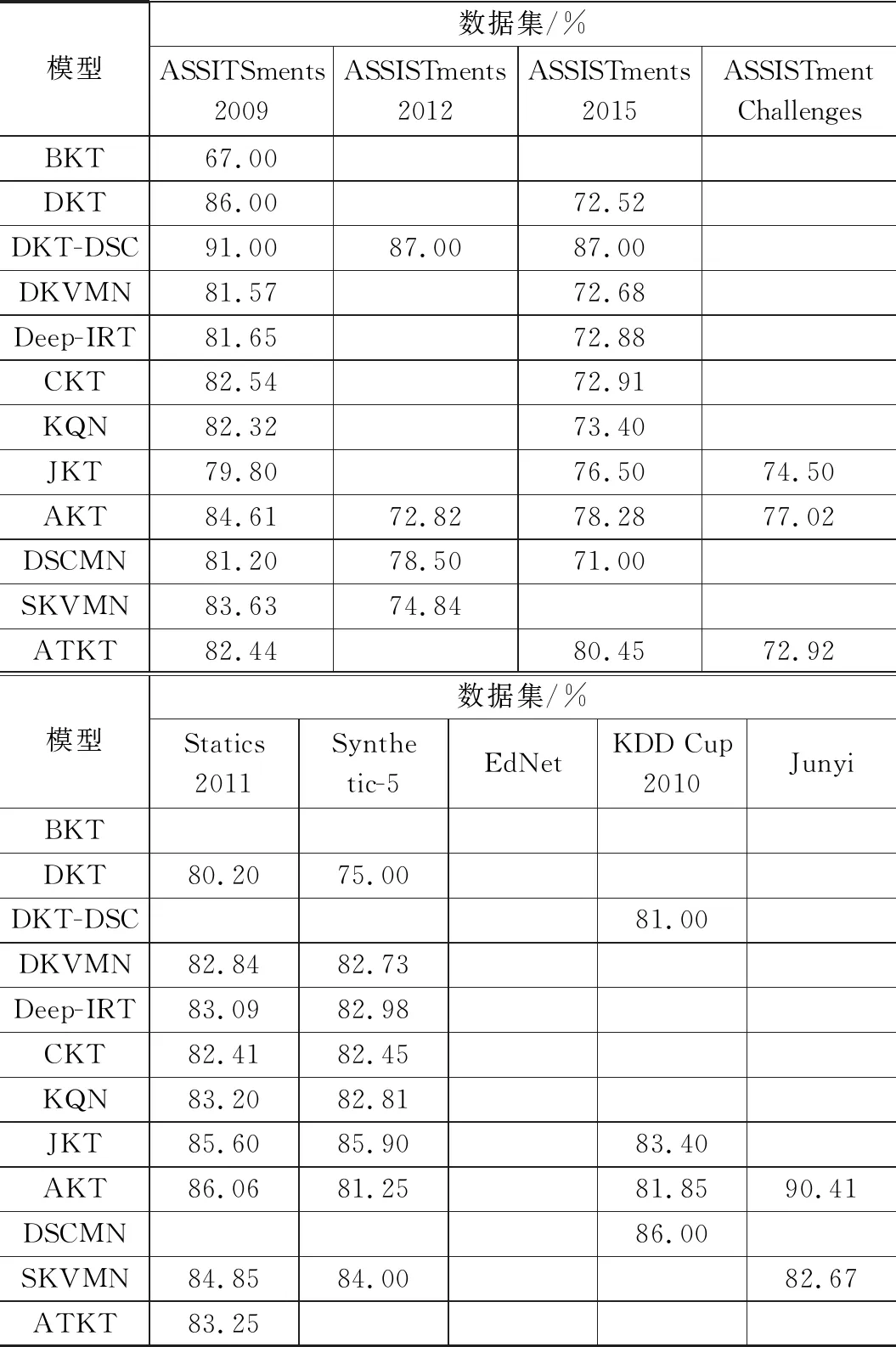
表3 模型性能(AUC)一览表

4 未来的研究方向

随着知识追踪在教育领域的应用与研究，其发展方向不断深入，主要包括调整学生知识结构、程序题的自动评测、学生个性化指导、预测学生掌握知识状态等，但目前知识追踪在起步阶段，同样也存在许多问题亟待解决，接下来总结了几个研究方向供研究者参考。

1)建模单一化问题：知识追踪领域的建模形式大多采用二元变量来描述学生的作答情况，知识追踪领域的数据主要来源在线学习平台，而学生的情绪未能记录在在线学习平台，而在实际教学过程中，想法多变的学生和种类多变的习题让知识追踪的准确率难以提升，研究学者提出关注学习过程中学生的情绪(无聊、困惑、遗忘等)，但由于学生在不同年龄段想法不同，因此，未来知识追踪会更加关注学生年龄问题对于建模问题的影响，根据不同年龄段的学生，及时进行教学计划的调整，实现个性化教学。如何将学生年龄信息并与其它信息进行融合等都是未来的重要研究方向。

2)主观题自动测评：随着人工智能与教育的不断发展，大部分研究工作者致力于客观题自动评测，已经有较好的成果，而主观题的测评由于“学习者随意发挥”，无准确评价标准，因此很多KT模型无法针对主观题进行建模，特别是针对程序自动测评，很多测评系统仅仅能评判程序正确与否，却无法给出程序的步骤分，而教育十三五规划要求培养信息化人才，因此程序的自动测评，将成为未来重要的一个研究方向。

3)针对不同领域建模：起初，知识追踪针对数学问题建模，由于每个学科都有其本身的特点，应用于数学问题的建模方式无法直接应用于其他学科，Cheng等人提出了自适应知识追踪(AKT)模型，但是由于AKT模型针对超参数较为敏感，因此，未来一个重要方向为如何解决不同学科的超参数问题，进一步提升知识追踪模型的准确性。

5 结束语

综上所述，在人工智能与教育相结合的大背景下，知识追踪作为智慧教学领域的主要研究方向之一，主要目的是获取学生的历史学习记录，追踪其随时间变化的知识状态，预测学生未来时刻的学习表现，从而实现个性化教学。本文主要集中近五年教育领域中的知识追踪模型，对该领域进行了全面的梳理与回顾，首先介绍了知识追踪领域经典的贝叶斯知识追踪(BKT)，并针对BKT介绍了其扩展模型,基于此模型，介绍了基于深度学习的DKT模型，并针对此模型的可解释性问题、缺少学习特征、缺少教育数据特征等问题进行扩展进行详细阐述；然后整理了知识追踪领域的公开数据集，对比了模型的性能；最后探讨了知识追踪领域现存的问题与未来的发展方向。