远海无人船编队系统AD HOC网络组播路由算法设计

李红卫，陈业程

(1.广东交通职业技术学院,广东 广州 510800；2.广东省船舶自动化工程技术研究中心,广东 广州 510800)

0 引 言

无人驾驶船最早出现于上世纪五六十年代，主要在遥控平台的近程海域作业。随着信息技术、通信导航、卫星定位以及智能控制技术的进步，其作业范围逐步拓展至远程海域。近年来，自主无人船是水面航行器研究的一个热点，特别在军事领域，目前世界上多个海洋强国开发了多种远程无人船平台以满足其军事和国家安全的需要。国内对远程智能无人船的研究起步较晚，虽然与欧美国家还有一定差距，但也取得了一定的成果。

虽然无人船的应用案例很多，优势明显，但是单无人船作业，其作业范围、作业时间、作业方式有限，且难以完成复杂任务。为了适应未来挑战，能够顺利、高效地完成复杂任务，除了提高单无人船功能和效用外，还需要实现及时、准确的多无人船编队调度，利用多艘无人船同时工作，更高效地完成任务，具有更强大的海上执行任务功能。

本文所述远海无人船编队系统包括船载控制系统和岸基控制系统。船载控制系统设置在无人船船体上，各无人船通过AD HOC网络节点设备实现相互之间信息交互，包括作业控制信息、自动定点作业、多无人船自主交互、多无人船组合导航、自主巡航、安全避障、自主循迹等信息。同时定义其中一AD HOC网络节点设备作为网络汇节点，由汇节点通过船载卫星通信终端实现无人船编队与岸基控制系统的信息交互。所述远海无人船编队系统如图1所示。

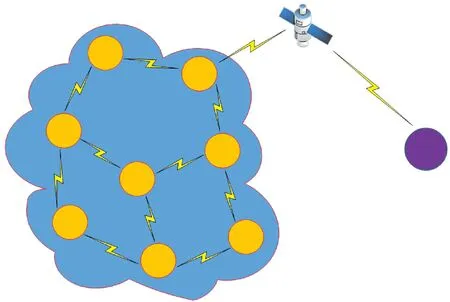
图1 无人船编队系统结构图

1 移动AD HOC网络主要特点

移动AD HOC网络是一种无中心自组织、没有预设基础设施的多跳无线网络，是由一组带有无线收发装置的移动节点组成的临时性自治系统，依靠网络内部具有移动性的节点之间的协作，完成节点间通信。与其它类型的无线网络(如蜂窝网、无线局域网WLAN、卫星系统)相比，具有以下主要特性[1]：

(1) 自组织性。AD HOC网络完全由无线节点组成，没有任何固定基础设施。所有节点地位平等，节点可随时加入和离开，具有较强的抗毁性。

(2) 动态拓扑。AD HOC网络具有动态特性，拓扑结构可以高度变化，所有节点可以任意移动(包括高速移动)。

(3) 多跳拓扑。无限节点通信距离有限，节点具有转发报文的能力，节点间的通信可能要经过多个中继节点的转发，这也是AD HOC网络与其他移动网络的最本质区别。

(4) 带宽有限且易变。无线信道本身的物理特性决定了它所能提供的网络带宽要比有线信道低得多。尤其野外情况下，由于复杂地形引起的多径、衰落、噪声及信道干扰、竞争共享无线信道所产生的碰撞等影响，带宽利用率低且无线链路容量容易发生变化。

(5) AD HOC网络的每个节点兼备主机和路由器功能，是无线通信技术与计算机网络技术相结合的产物。

总之，AD HOC网络是一种移动、无线、多跳的分布式网络。为了进行有效通信，必须在移动主机间建立合适的路由，所以设计快速、高效、健壮的路由算法极为必要[2]。

2 选路算法

当源节点S需要在本地路由表中寻找一条到目的节点D的最优路由时，可以采用多种算法，如果考虑链路的权值(如传输速率、误码率等)，则最优路由是从S到D的所有链路的权值或者代价总和最小的一条路由。

本系统AD HOC网络节点间的数据传输采用源路由方式，即每一个节点都需要维护一张到达全网其它节点的系统路由表，数据以源路由选项夹带发送，中间节点不参与选路过程。系统路由表基于全网链路质量矩阵(动态、静态、混合3种)，采用最短路径算法(Dijkstra)计算而得，链路质量为由接收信噪比与物理层数据传输误码率及阻塞率计算得出的0～7的数值[3]。

Dijkstra最短路径算法是典型的最短路径算法，用于计算一个节点到其他节点的最短路径。即以本节点为起点，不断加入最短边，最终得到目的节点的最短路径。

该算法的具体描述如下：

集合S：存放已求出最短路径的顶点，初始时，S中只包含起点即源节点v0。计算过程中求得的每一条最短路径(v0, …vk)都放入集合S中，直到求出全部顶点算法即结束。

设置辅助数组d，其每一分量d[i]表示当前找到的从源节点v0到终点vi的最短路径的长度。若从源节点v0到终点vi有路径可达，则将该路径即该边权值放入d[i]；若从源点到终点没有路径可达，即认为距离为+∞，并将+∞放入d[i]。

(1) 假设第1条最短路径为(v0,vk),并且k满足：d[k]=min{d[i] ∣vi∈V-v0}，V为所有顶点集合。

(2) 求下一条最短路径：假设下次最短路径的终点是vj，则它要么是(v0,vj)，要么是(v0,vk,vj)。其长度要么是从v0到vj边上的权值，要么是d[k]与从vk到vj边上的权值之和。

可知下一条次短的最短路径的长度必是：d[k]=min{d[i] ∣vi∈V-S}。

(3) 集合S存放每一次已经求出最短路径的终点，然后对所有的vi∈V-S，修改其d[i]:d[i]=min{d[i],d[k]+e[k][i]}，e[k][i]为边(vk,vi)上的权值。

算法的核心是综合链路权重，表示为：W(i,j)=αQ(i,j)+βD(i,j)+c。其中，Q(i,j)表示链路i→j的链路质量；D(i,j)表示链路i→j的延迟参数；α和β为权值；c为恒定参数；参数的不同选择，决定了算法的适用环境：

(1) 当α=0时，算法为延迟最小路由算法；

(2) 当β=0时，算法为链路质量最大路由算法；

(3) 当α=0，β=0时，算法为传统的最小跳数路由算法；

(4) 当α>0，β>0时，算法为综合最优路由算法。

在本系统中，取α=1，β=1，c=0，综合链路权重W(i,j)主要依据全网链路质量矩阵(动态路由方式下为全网动态链路质量矩阵；静态路由方式下为全网静态链路质量矩阵)和节点负载，每一条链路Q(i,j)均考虑了正反向的链路状况，为正反链路质量之和(即系统路由决定于节点间的双向链路)。此处的链路质量并非节点间真实的链路质量，而是由链路质量矩阵经转换而得，转换规则如下：

(1) 链路质量为0，则转换后的值为240；

(2) 链路质量为1，则转换后的值为60；

(3) 链路质量为2，则转换后的值为10；

(4) 链路质量为3，则转换后的值为9；

(5) 链路质量为4，则转换后的值为8；

(6) 链路质量为5，则转换后的值为7；

(7) 链路质量为6，则转换后的值为6；

(8) 链路质量为7，则转换后的值为5。

另外，对于链路的2个顶点，还考虑了该节点数据发送缓冲的当前拥塞系数(即可能造成的传输延时)。

3 组播路由算法

3.1 算法思想

求出满足约束条件下的基于最少中继节点的最小代价组播树，算法分为以下两步：

(1) 求出满足约束条件下代价最小的组播树；

(2) 合并中继节点，使得到的组播树中的中继节点最少。

3.2 代价函数及约束条件

在组播路由中，链路代价函数cost主要由链路质量及节点负载构成。

约束条件主要包括最大跳数约束、最小代价约束和最小性资源消耗约束。最大跳数约束：从源节点到目的节点的路径长度，必须低于给定的门限值(这里限定为6跳网络)；最小代价约束：生成的满足最大跳数约束的组播树的总体代价最小；最小性资源消耗约束：根据无线网络的特点，某节点发送一次数据，其邻居节点都能收到，如果组播树的中继节点越少，分配给中继进行数据转发的时隙越少，资源消耗越少。

同时在选择路由时需要合理考虑流量平衡问题，一个基本原则就是到不同目的节点尽量使用不同的中继节点。如果到同一目的节点存在多条长度相等但经过不同中继节点的路由，则每次发送数据时也尽量使用不同的路由，这样有利于实现转发节点的流量平衡，避免出现转发数据大量堆积在某个中继节点而无法及时得到转发的情况。

3.3 算法描述

为描述算法，给出几个定义：T表示生成树，T′用来存储节点跳数按升序排序后的生成树。R指生成树中的源节点s和目的节点集合D以外的节点。Dk表示D中满足跳数要求的目的节点集合。

最小路径：2个节点之间的最小路径是指这2个节点之间代价最小的路径；某节点到最小生成树的路径是指该节点到树的各节点最短路径中代价最小的那条。节点到树的最短路径也被称为树到节点的最短路径，节点到树最短路径的代价称为节点到树的最短距离[4]。

算法具体步骤如下：

(1) 求满足跳数约束的最低代价组播树，如图2所示。

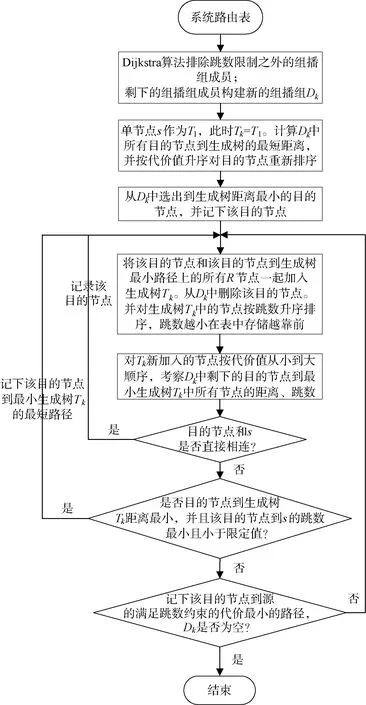
图2 求满足跳数约束的最低代价组播树算法流程图

(2) 合并中继，流程图如图3所示。

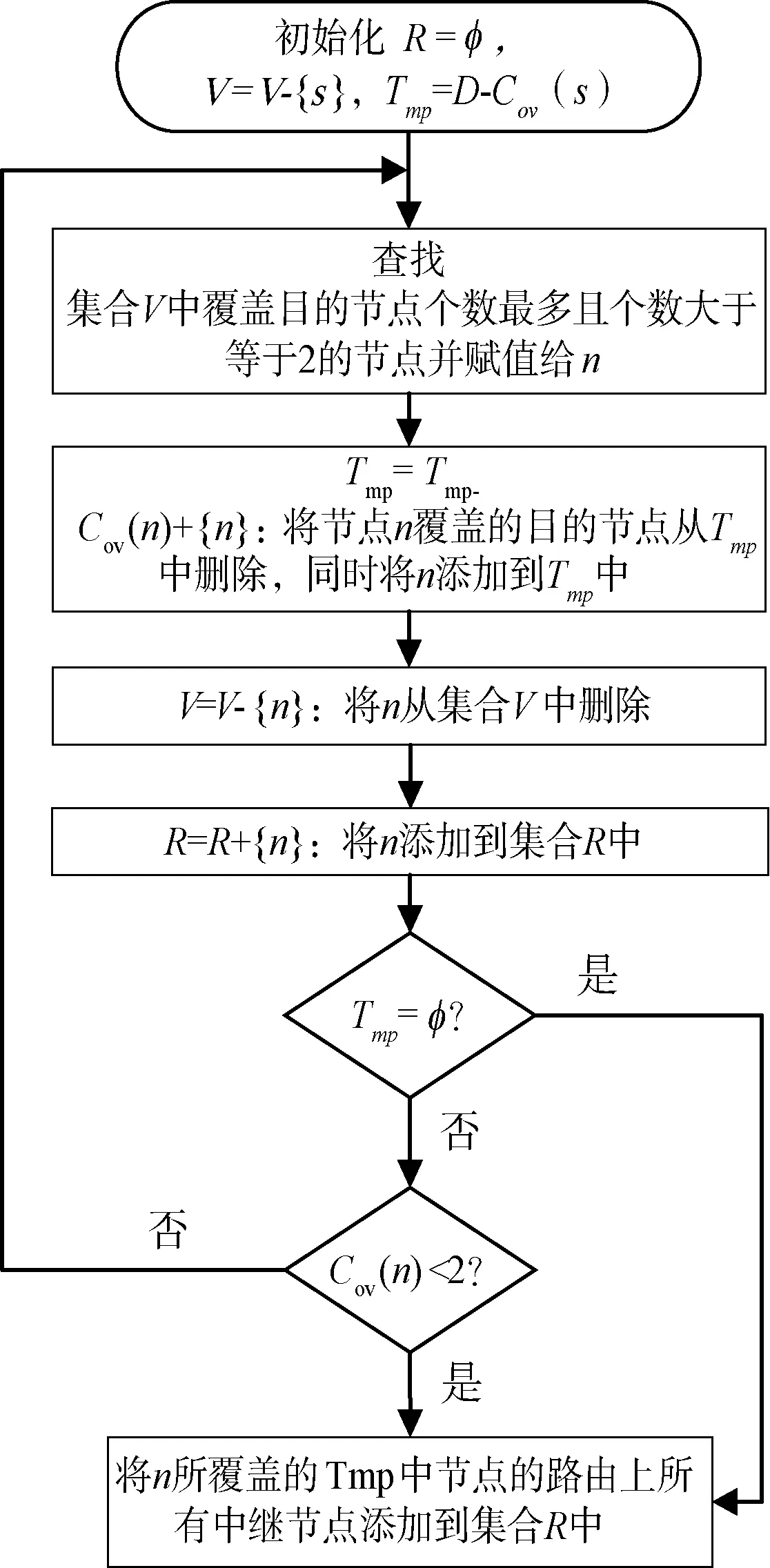
图3 合并中继算法流程图

定义：V为最小生成树中所有节点集合，R为中继节点集合，Tmp为临时节点集合，n为临时节点。Cov(v)为节点v所覆盖的目的节点集合。

最终所求组播树的构成如下:

(a) 首先,包括所有的目的节点,即D内的所有节点,设置节点类型为目的节点；

(b) 其次,包括R内所有节点,节点类型为中继节点,如果,该节点同时为目的节点,则设置节点类型为中继或目的节点。

3.4 应用实例

网络拓扑：源节点S，目的节点C、D、E、F、G。网络拓扑结构图如图4所示。

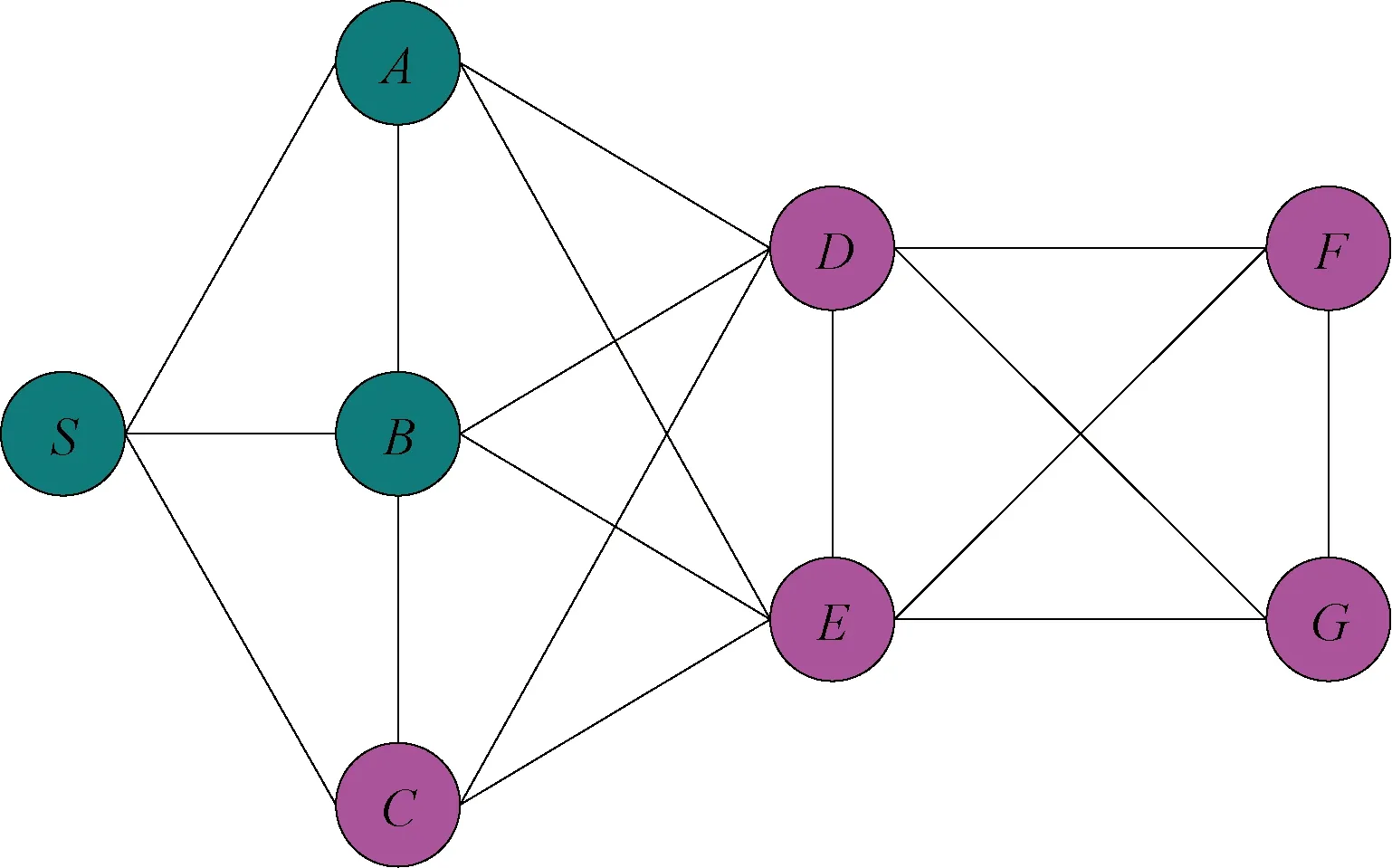
图4 网络拓扑结构图

通过Dijkstra最短路径算法求得的最短路由树如图5所示。

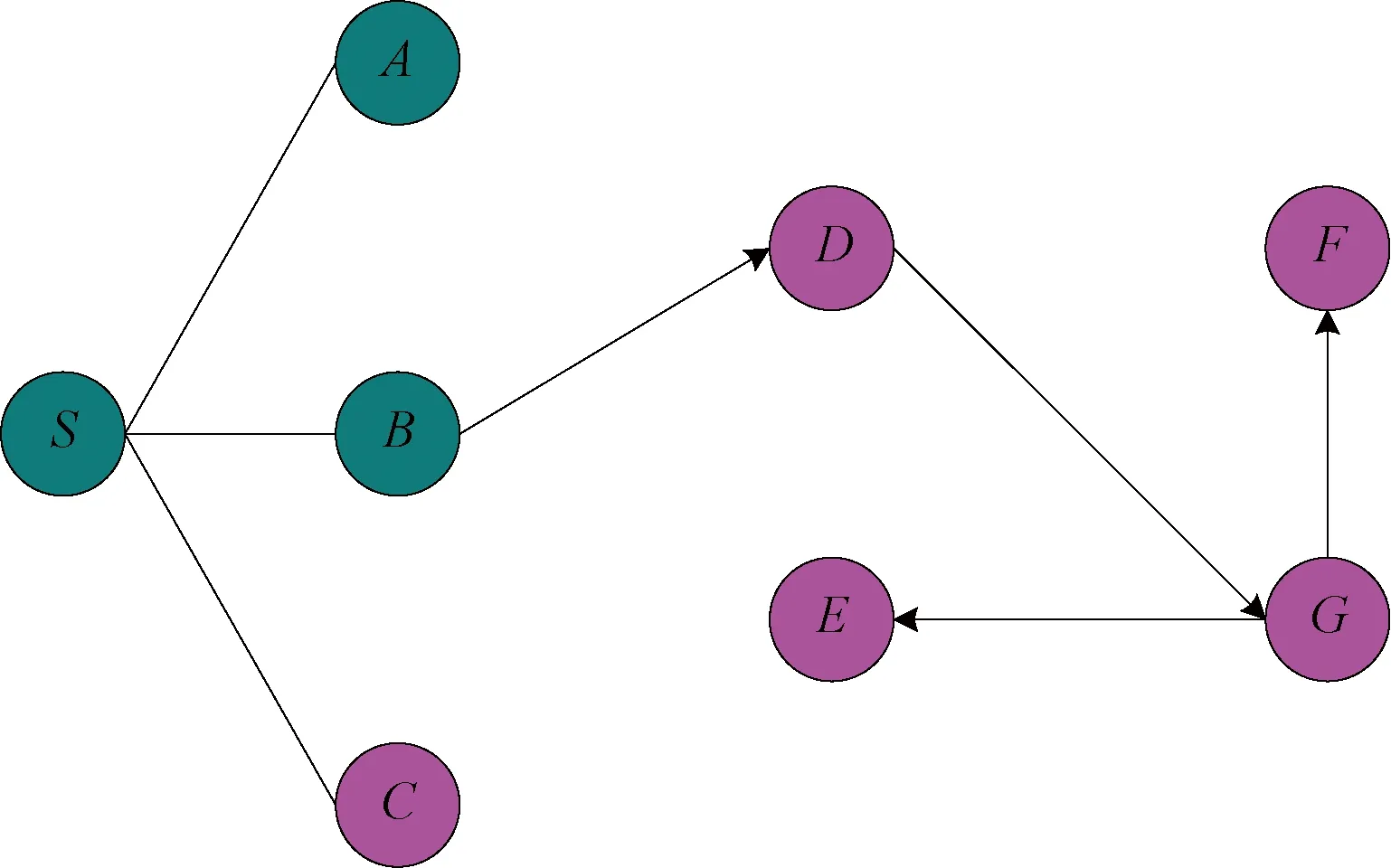
图5 最短路由树结构图

算法详细步骤：

(1)MF=φ，V= {B，C，D，E，F，G}，Aux={C，D，E，F，G}；

(2) 源节点S覆盖的目的节点C，将C从Aux中删除：Aux={D，E，F，G}；

(3)n=G，因为Cov(G)={E，F}，覆盖目的节点个数最大，Aux={D，G}；V={B，C，D，E}；MF={G}；

(4)Aux中所有节点覆盖目的节点个数均小于2，n=null，停止；

(5)Aux！=φ，所以查找路由表，发现路由{S，B，D}和{S，B，D，G}，将这2条路由的所有中继添加到MF中，则MF={B，D，G}；

(6) 所以源路由为：{S，B，C，D，E，F，G}，其中S为源节点，B为中继节点，D，G为中继或目的节点，C，E，F为目的节点。

最终得到的最小组播路由树如图6所示。

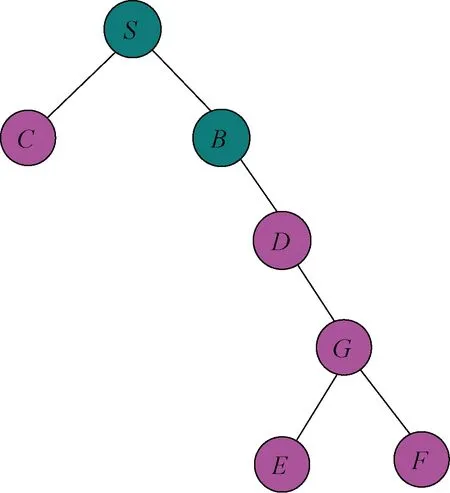
图6 最小组播路由树结构图

在综合平衡最大跳数约束、最小代价约束和最小性资源消耗约束等约束条件情况下，获得基于最少中继节点的最小代价组播树。该最小代价组播树包含所有源节点、目的节点、最短路由边的拓扑矩阵，使得发送数据时，将数据沿着尽可能多的覆盖目的节点的路径传输，可以减少路由请求次数，减少网络开销，在最短的时间内将数据传送到各个目的节点。

4 仿真测试

本方案中采用OPNET Technologies Inc公司的OPNET网络仿真工具对组播协议进行仿真。在AD HOC网络中，每个节点都是对等节点，即每个节点都可以作为服务器，也可以作为客户端，且所有节点可以产生的业务也是相同的。因此，所设计的组播路由算法的仿真采用wlan_server_adv通用平台，其节点模型如图7所示。

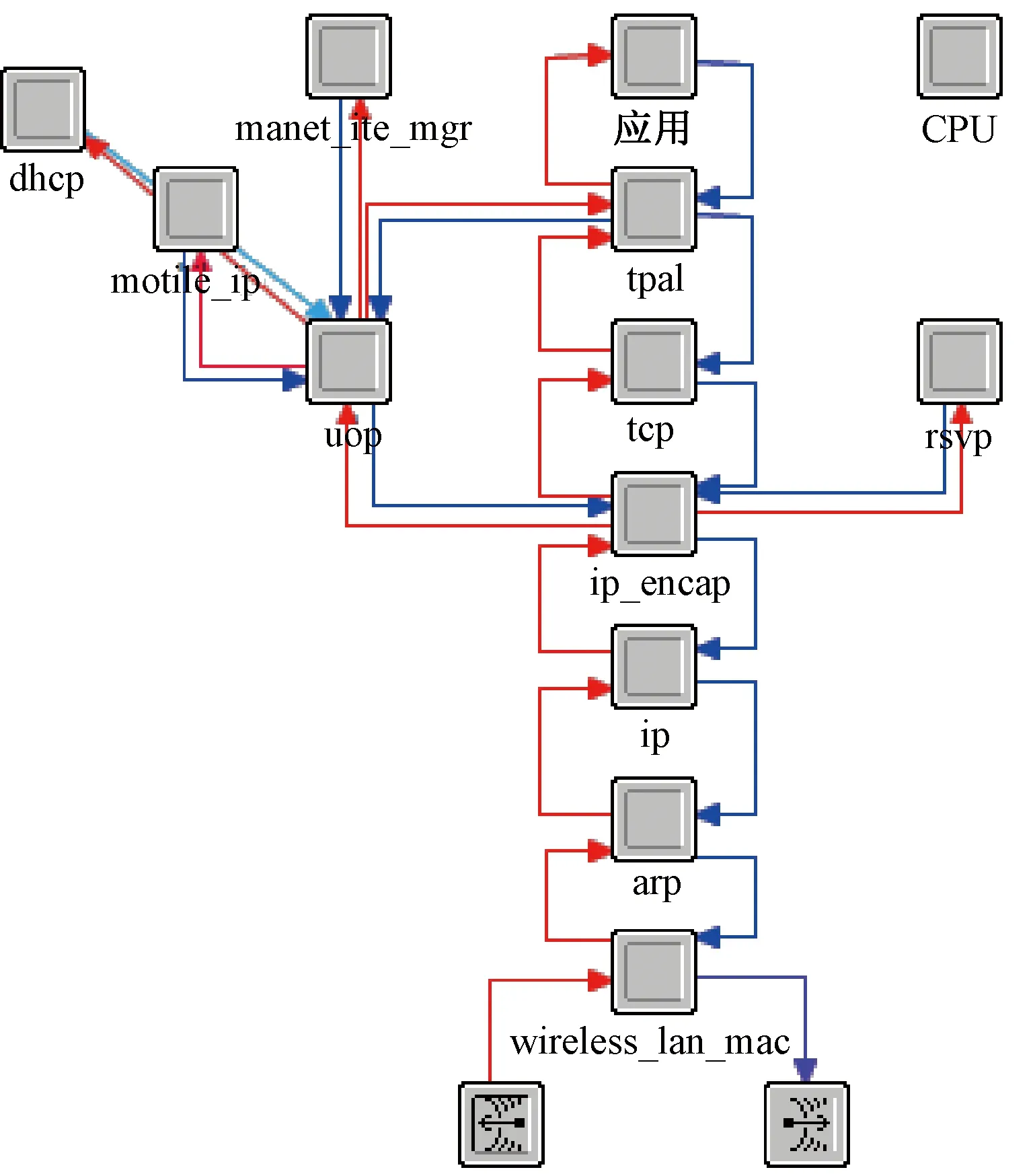
图7 仿真节点模型

对于所设计的组播算法的性能优劣主要通过与Internet网络比较指标得到，在此比较丢包率和时延参数。在该仿真试验中，若某个节点发送数据包之后，如收到目的节点回复ACK即认为发送成功，否则认为发送数据包丢失。

丢包率的计算公式可以写为：丢包率=(发送数据包数-收到ACK数)/发送数据包数。时延为一次完整通信过程所持续的时间，即数据包从源节点到目的节点所占用的时间。

本仿真中定义丢包率为同网络规模下的平均数据传输丢包率，时延为不同网络规模下的平均传输时延。图8为移动AD HOC网络与Internet网络在不同网络规模下的平均数据传输丢包率，图9为移动AD HOC网络与Internet网络在不同网络规模下的平均传输时延。

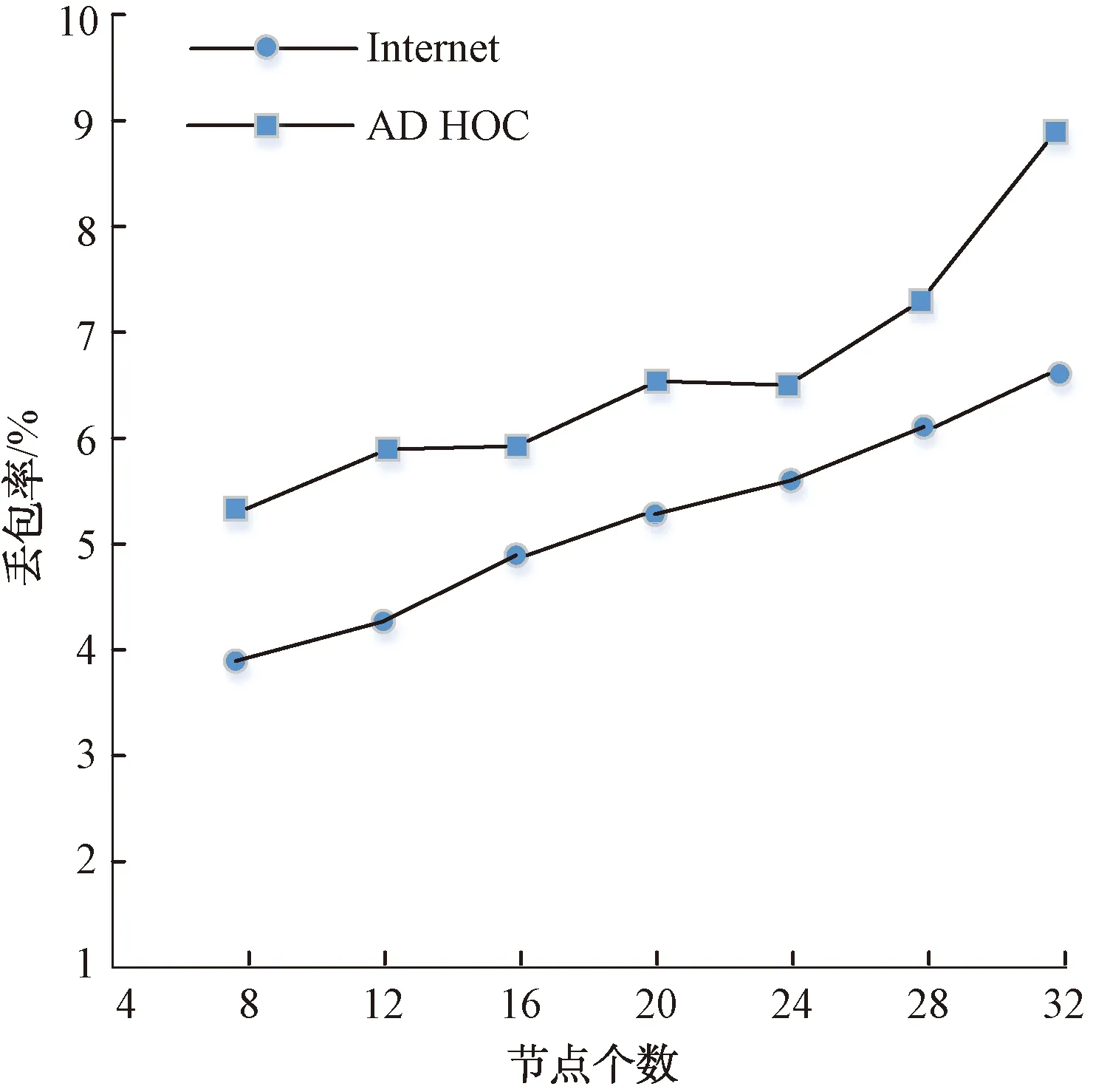
图8 AD HOC网络与Internet网络数据传输丢包率仿真曲线

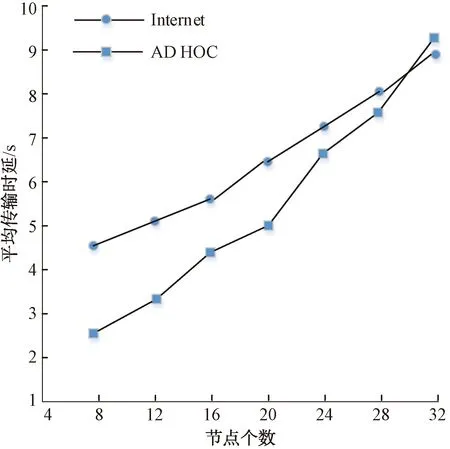
图9 AD HOC网络与Internet网络数据传输时延仿真曲线

从以上仿真结果可知当节点数在32个以内时，移动AD HOC网络移动Internet网络的数据传输丢包率性能相当，而AD HOC网络的时延，明显小于Internet网络的时延，说明设计的组播路由算法在AD HOC网络规模较小时具有较高的信号传输效率，且信号失真率低[5]。随着节点数量的增加，2种网络的信号传输时延逐渐相同。

5 结束语

自主无人船是无人船编队水面航行器研究的一个热点，在未来将得到大力发展。为满足无人船编队自组织网络的数据传输需求，本文基于移动 AD HOC网络设计组播路由算法，以便网络节点按组工作完成给定任务。本文设计了改进的Dijkstra最短路径选路算法，通过选路算法求出节点到节点之间的最短路径，通过合并中继可求出最小组播路由树。仿真比较不同网络规模下AD HOC网络与Internet网络的传输性能，验证了该算法具有良好的数据传输效率。不同网络的节点数据传输仿真试验表明，该组播路由算法具有良好的数据传输效率。