基于北斗与超宽带组合定位的改进算法设计

岳 鹏，刘怀远，党 方，张泽仑

(中国电子科技集团公司第二十研究所，陕西 西安 710068)

0 引 言

近年来，国内外学者针对传统北斗与超宽带组合定位算法的不足，从各个领域对高精度定位算法进行了研究，典型的包括基于GPS和UWB之间信息数据组合问题提出的一种自适应变分贝叶斯容积卡尔曼滤波算法、GPS/UWB/INS(Inertial Navigation System)组合定位自适应鲁棒卡尔曼滤波算法、GPS/UWB/MARG(Microprocessor Magnetic Angular Gravity)组合加权融合定位算法等等。通过对前学者们的研究结果进行分析总结，发现单一的牛顿迭代最小二乘定位算法是对单一历元进行定位解算，没有考虑位置在时间上的连续性，因为在时间上没有进行相关处理所以导致牛顿迭代-最小二乘的定位结果是粗糙且杂乱无章的，而单一的滤波算法需要较为精准的初始位置估计。将二者进行级联，通过滤波器对牛顿迭代最小二乘的输出结果进行再次处理，可以得到较为精准的定位结果，所以将核心算法部分基于上述级联算法进行开展，得到定位精度更高以及抗干扰能力更强的定位算法。

本文以满足高精度的位置服务需求为出发点，以北斗超宽带组合定位的伪距融合模型为基础，主要研究LS-α-β滤波级联定位算法和LS-KF级联定位算法，并在LS-KF定位算法的基础上提出了改进型自适应加权WLS-KF级联定位算法。

1 融合模型

北斗超宽带组合定位的伪距融合模型如图1所示。在每个需要定位的目的点上放置一个处理器，该处理器不同于一般的北斗接收机，是一个综合多功能处理器。它可以接收北斗的信号，并将接收到的北斗信号所携带的卫星坐标、伪距、钟差校正等信息解析出来，然后将这些信息传递给数据处理中心。同时定位目的点上的综合多功能处理器也可以发射UWB信号，各个UWB接收基站会接收来自定位目的点的UWB信号并根据测距算法从中解析出测距信息，然后将该距离信息以及相对应的UWB基站坐标转发到数据处理中心，这样数据处理中心就同时接收到了来自于北斗和UWB两个定位子系统的信息数据。本文主要涉及特定的智能优化定位算法将BDS/UWB综合观测方程进行解算，从而得到目的定位点的三维坐标信息。

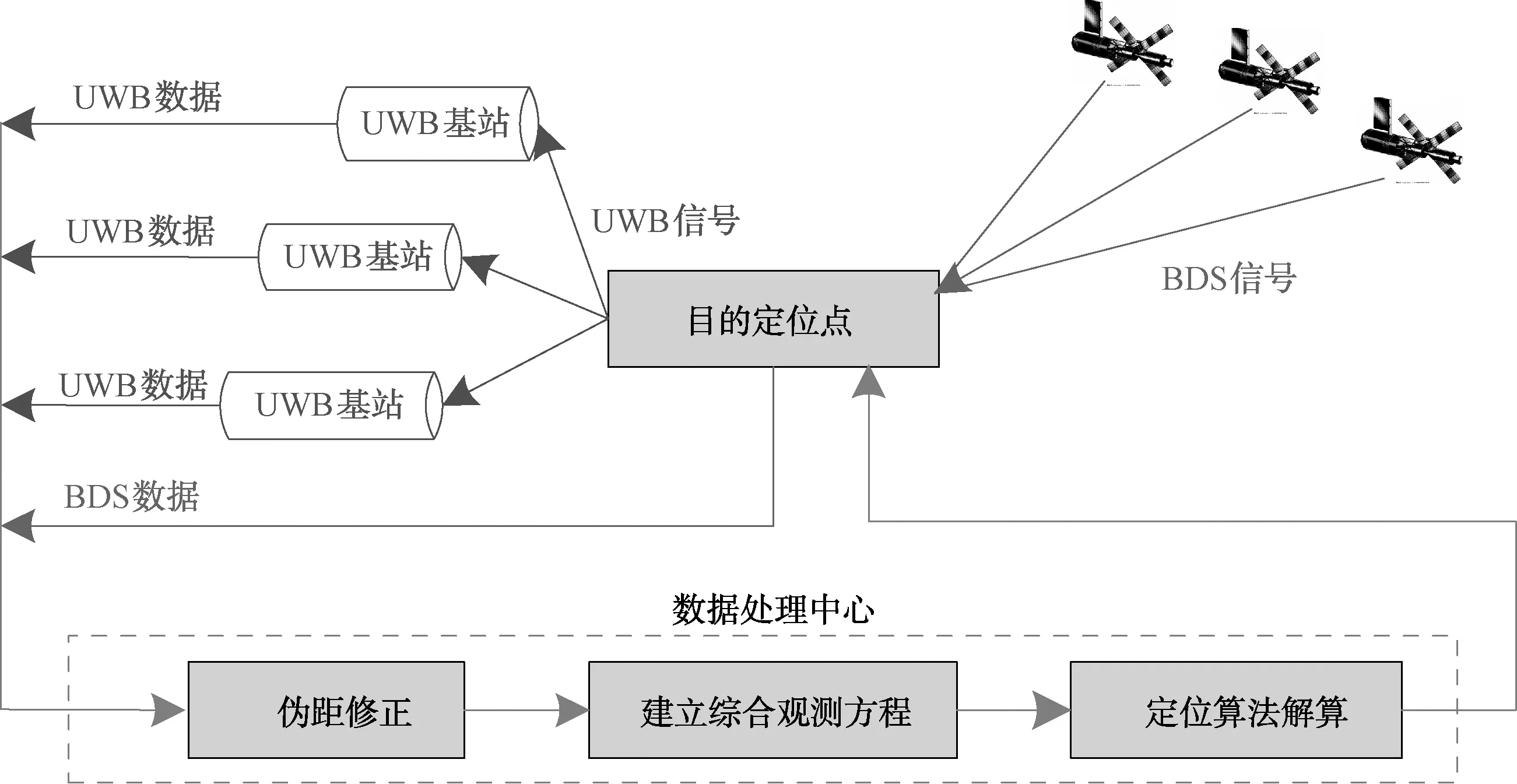
图1 BDS/UWB组合定位的伪距融合模型

2 综合观测方程

将BDS的数据和UWB伪卫星的数据进行融合，建立BDS/UWB综合观测方程，才算是将BDS和UWB进行了紧耦合处理。可以将2个子系统的方程进行联立来求解，以获得高精度的定位结果，将各自子定位系统的方程进行组合能够得到如下所示的BDS/UWB综合观测方程：

(1)

将式中的对流程误差、电离层误差以及钟差等建立相应的补偿校正模型进行补偿，校正后的BDS/UWB综合观测方程为：

(2)

3 LS-KF级联定位算法

在LS-α-β滤波级联算法中，主要通过α-β滤波技术对最小二乘的解算结果进行滤波，使得最终的定位结果更加平滑、准确。但是α-β滤波技术的缺点之一就是它采用固定滤波系数对系统状态向量的先验估计以及测量进行加权处理来获得系统状态的最优估计，未考虑在不同观测时刻测量值可能会存在不同的误差。采用LS-KF级联定位算法对BDS/UWB综合观测方程进行解算处理时，对于每一观测历元下的定位解算首先采用牛顿迭代-最小二乘定位算法对非线性的综合观测方程进行解算，得到时间上不相关的粗糙解；然后用卡尔曼滤波器，对最小二乘的解算结果进行滤波处理以得到更高精度的用户三维定位坐标。

图2为在BDS3+UWB组合定位系统中LS-α-β滤波级联定位算法和LS-KF滤波级联算法定位误差对比分析曲线。从图中可以看出，在最开始的10个观测历元之内，LS-α-β滤波级联定位算法的性能要优于LS-KF滤波级联算法，而LS-KF滤波算法需要一定的时间才可以收敛到高精度的定位。但是随着观测历元数量的增加，LS-KF逐渐表现出了更优秀的定位性能。从仿真结果中可以看出，LS-α-β滤波级联定位算法在300个观测历元下的平均定位误差为0.58 m，而LS-KF滤波级联算法在300个观测历元下的平均定位误差可以下降到0.29 m，相比于LS-α-β算法LS-KF算法有着约50%的定位性能提升。

图2 LS-KF定位算法与LS-α-β滤波级联定位算法性能对比

图3为BDS/UWB组合定位系统中的LS-α-β滤波级联定位算法和LS-KF滤波级联算法处于站心坐标中的定位散点图，球心代表着待定位点，周围的散点代表着每一观测历元下得到的解算定位点，解算结果越靠近球心证明定位性能越好。从图3所示的仿真结果中可以看出，LS-KF算法的定位结果虽然有几个点偏离球心但整体上相比于LS-α-β算法更趋向于球心。

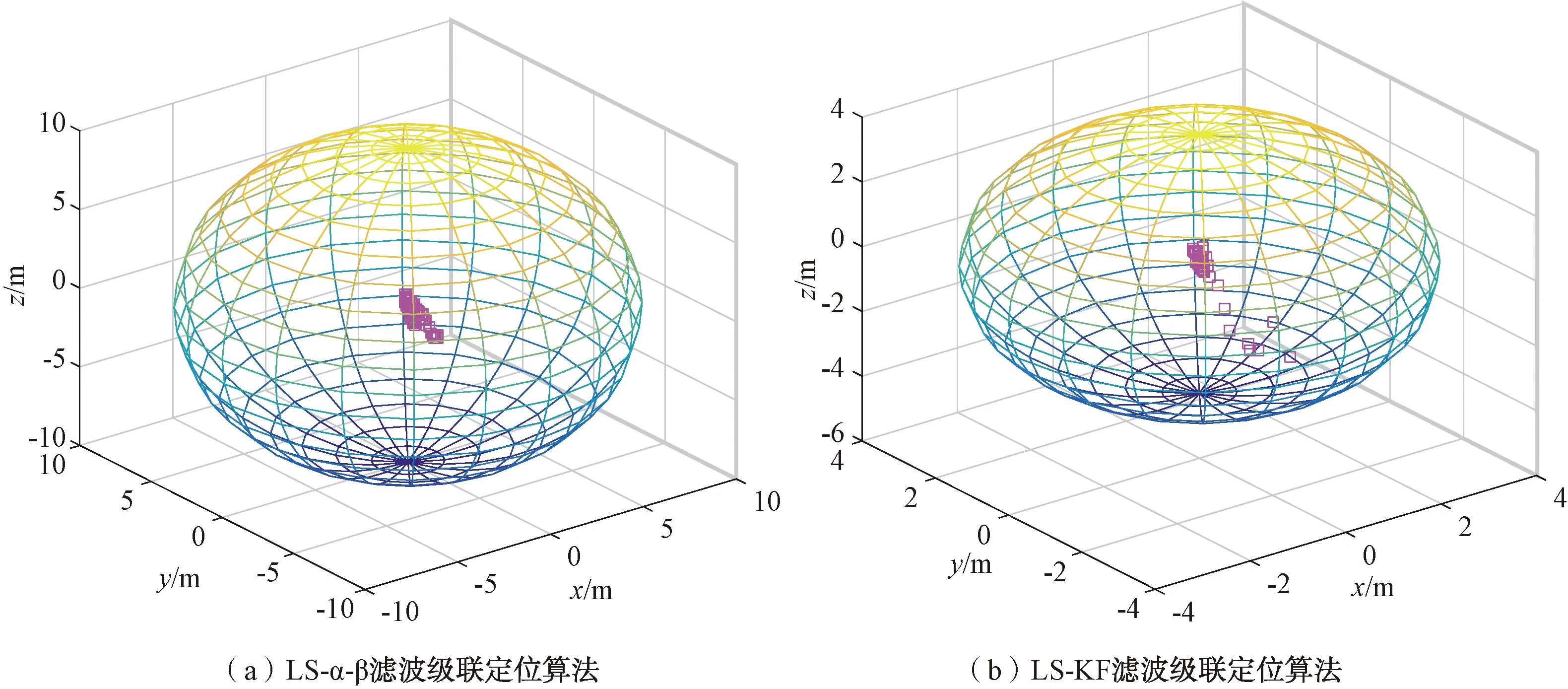
图3 定位结果三维散点图

4 自适应加权WLS-KF级联定位算法

在BDS/UWB组合定位系统中，由于应用环境较复杂，所以信号会经常受到遮蔽、多径等影响而造成某些观测量误差较大的现象。也就是说即使在同一个BDS/UWB综合观测方程组中，不同的观测方程之间的测量误差是会有着较大差异的，此时如果继续采用等权的方式就会使定位结果出现偏差。在这种情况下，就应该对BDS/UWB综合观测方程组中不同的观测方程赋予不同的权重，对测量误差较小的观测方程赋予较大的权重，对测量误差较大的观测方程赋予较小的权重。针对这个问题，提出了一种基于伪距残余检测的自适应加权最小二乘法和卡尔曼滤波级联的定位算法，即自适应加权WLS-KF定位算法，数据处理过程如图4所示。

图4 自适应加权WLS-KF算法数据处理过程示意图

对于BDS/UWB组合定位系统的定位算法来说，应该充分考虑到不同观测卫星和UWB之间的权重问题，信息数据越可靠应该赋予越大的权重；反之，赋予较低的权重。提出基于伪距残余检测的自适应加权方式计算步骤如下：

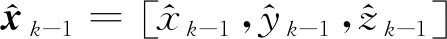
(3)

然后求得先验预测伪距和接收到伪距之间的残差：

3.1.1 精心选编案例，提高学生学习效果 学生尚未接触临床，没有实际经验的积累，因此，案例一定要来源于临床实际，既贴近临床岗位又贴近生活，具有代表性；要紧紧围绕教学大纲和教学内容要求，考虑学生现有知识和技能水平下的接受理解能力，创设与教材内容相辅相成的具体、真实的场景问题，使学生有身临其境的感觉，实现理论与实践相结合。

(4)

(2) 根据先验估计的伪距残差进行定权，伪距残差较大的应在最小二乘中赋予较小的权重因子，伪距残差较小的应在最小二乘中赋予较大的权重因子。因此可以将权重设置为相应残差的倒数，得到的权重矩阵为：

(5)

(3) 求加权最小二乘解，需要将各个方程式乘以相应的权重，则线性化后的矩阵方程经过加权处理变为：

(6)

现在通过最小二乘法来求解矩阵方程，在这里对最小二乘的中间过程就不再赘述。直接套用最小二乘的求解公式求得：

Δx=(GTWTWG)-1GTWTWb

(7)

这种基于伪距残余检测的加权方式，在每一个观测历元下的权重都是不同的，每一次都可以根据最新先验伪距残余检测结果自适应地调整权重矩阵。

5 性能分析

本节仿真采用4颗北斗卫星和1个超宽带辅助基站，也就是BDS4+UWB的组合定位方式。对于BDS系统的伪距设置的噪声依旧是均值为0、方差为1的噪声序列；UWB的测距误差设置的仍然是均值为0、方差为0.2的噪声序列，但是此次仿真研究了持续性干扰和突发性干扰对所提算法的影响。对于持续性干扰的研究，仿真中在第100～200个观测历元下的第1颗卫星伪距中加入了10 m的伪距干扰，在第200～300个观测历元下的第2颗卫星伪距中加入了10 m的伪距干扰。对于突发性干扰的研究，仿真中分别在第80、120、160、200以及240个历元下的第1颗卫星伪距中加入了20 m的突发性干扰。

图5为在无干扰或无其他突发情况时LS和WLS定位性能对比分析，从仿真结果中能够看出原来的最小二乘定位算法的平均定位误差为2.51 m，而采用提出的基于伪距残余检测的自适应加权最小二乘算法的平均定位误差为2.32 m，定位性能有约8%的提升。

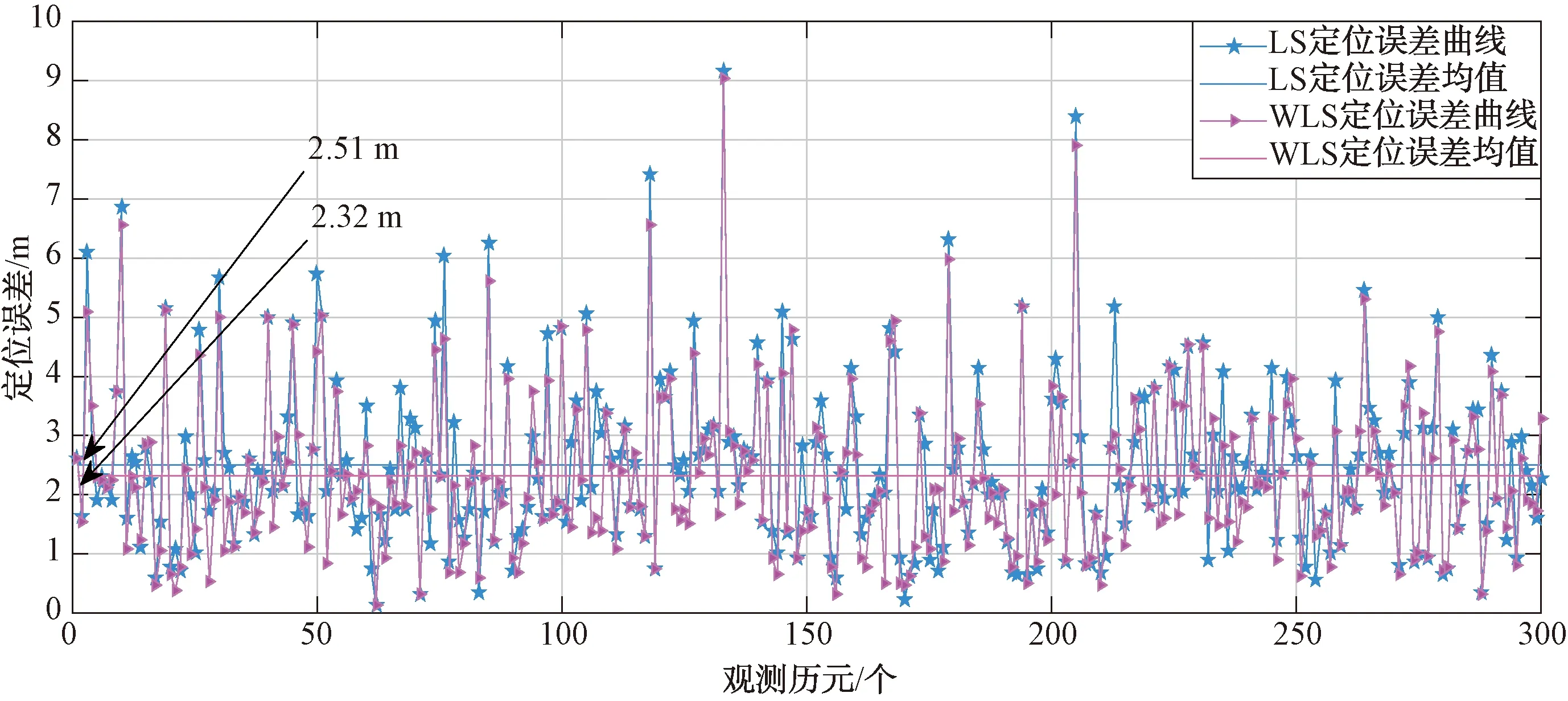
图5 无干扰时LS和WLS定位性能对比分析

图6为在无干扰或无其他突发情况时LS-KF和WLS-KF定位性能对比分析，从仿真结果中能够看出在大多数观测历元下WLS-KF的定位误差都是小于LS-KF算法的。在300个观测历元下LS-KF算法的平均定位误差为0.20 m，而采用提出的基于伪距残余检测的自适应加权WLS-KF算法的平均定位误差为0.18 m，定位性能有约10%的提升。

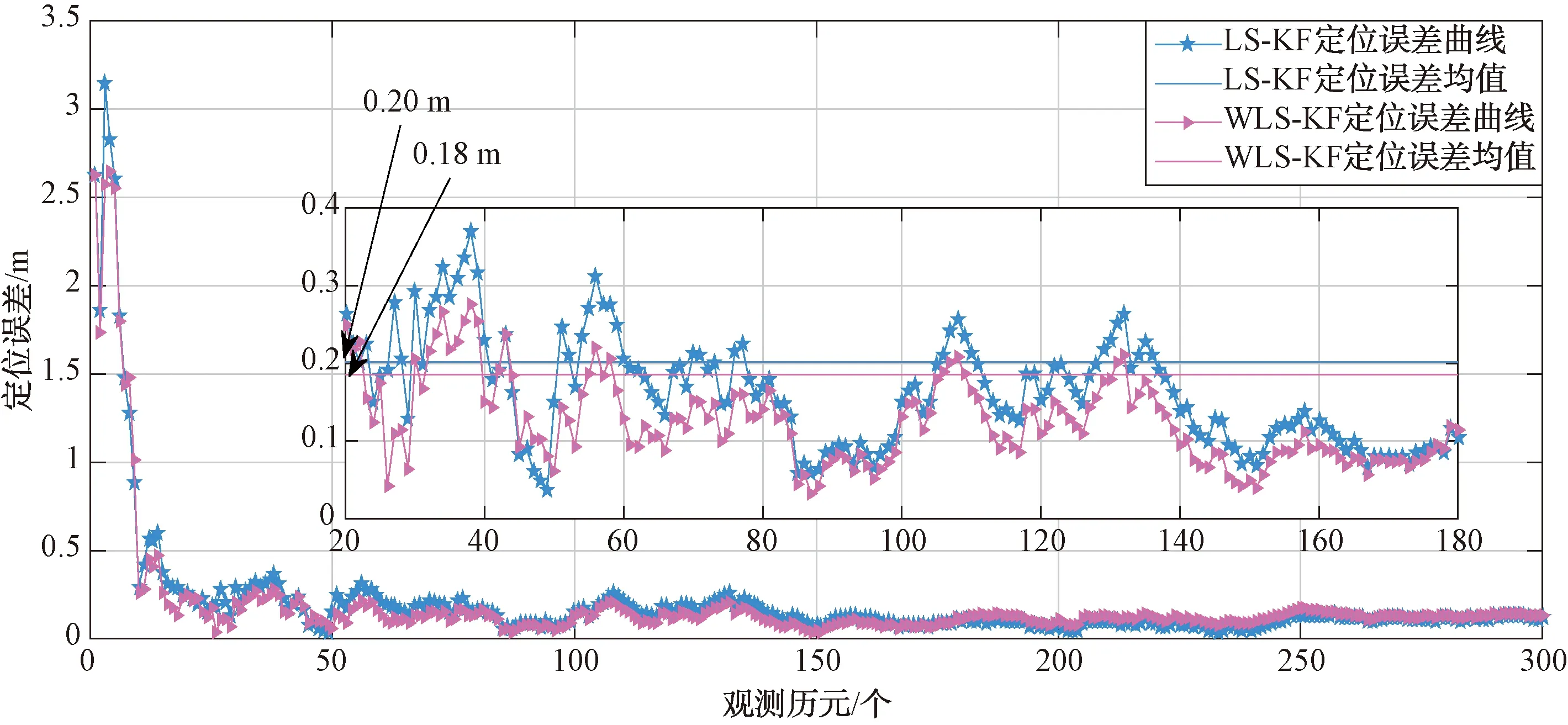
图6 无干扰时LS-KF和WLS-KF定位性能对比分析

图7为当存在一些突发性干扰时LS和WLS定位性能对比分析。图中用椭圆形圈出的地方为存在干扰时2种算法各自的定位性能，能够看出WLS算法在干扰存在时也会受到干扰的影响而使定位误差增加，但是它的抗干扰能力明显优于LS算法。从仿真结果中能够看出，原来的LS算法的平均定位误差为2.77 m，而采用提出的基于伪距残余检测的自适应加权WLS算法的平均定位误差为2.43 m，定位性能有约12.3%的提升。

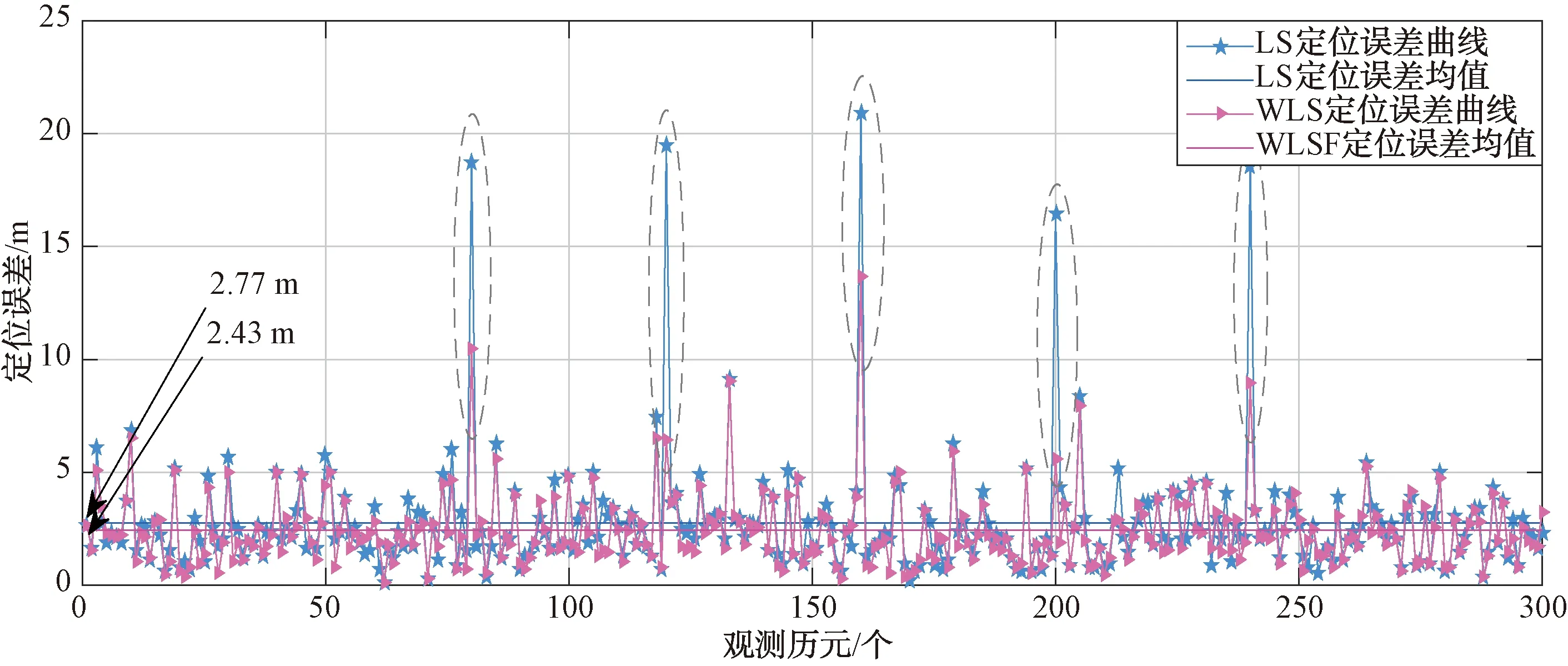
图7 突发性扰时LS和WLS定位性能对比分析

图8为当存在一些突发性干扰时LS-KF和WLS-KF定位性能对比分析。观察图8中基于伪距残余检测的自适应加权WLS-KF定位算法，能够明显看出它的定位误差是低于LS-KF算法的，在300个观测历元下它的平均定位误差为0.22 m，原LS-KF的平均定位误差是0.35 m，所提出的算法相比于原来的算法在定位精度上能够提升约37%。图中椭圆形圈出的地方为存在干扰时的定位误差，能够看出当存在干扰时LS-KF算法的定位误差会明显上升，这说明该算法的抗干扰能力较差，而WLS-KF在面临干扰时定位误差也会有所增加但是不会很明显，这也就意味着所提出的这种算法具有很强的抗突发性干扰的能力。

图8 突发性扰时LS-KF和WLS-KF定位性能对比分析

图9为当存在持续性干扰时所提出的基于伪距残余检测的加权方式对LS以及LS-KF算法的改进作用。从仿真结果能够看出，采用所提的方式进行加权处理能够提高LS和LS-KF算法的定位精度以及它们抗持续性干扰的能力。从图9(b)中能够看出在第100～200个观测历元期间，卡尔曼滤波器出现了持续发散现象，这是因为在这期间，持续存在干扰导致最小二乘的误差较大，就会间接影响到卡尔曼的滤波性能。而在第200～300个观测历元期间，LS-KF算法持续发散，这是因为在这期间LS误差较大，所以导致级联着的滤波器发散，而WLS-KF算法逐渐收敛，这是因为在这期间WLS的误差逐渐减小，使级联着的滤波器也随之收敛。

图9 持续性干扰时定位性能对比分析

综合以上仿真结果能够看出，对LS算法和LS-KF算法采用基于伪距残余检测的加权方式形成新的WLS算法和WLS-KF算法能够提高定位精度，增强定位的稳定性，使它们在面临一些突发性干扰或者持续性干扰时都尽量能保持较好的定位性能。

6 结束语

本文主要研究了BDS/UWB组合定位改进算法。首先针对不同观测量间的定权问题提出了基于伪距残余检测的自适应加权WLS-KF定位算法，充分考虑到不同的观测卫星和UWB之间的权重问题，信息数据越可靠赋予越大的权重，反之赋予较低的权重。仿真结果显示该算法相比于LS-KF算法在定位精度以及抗干扰能力上都有较大的提升，对于我军民用及军事领域均有一定的借鉴意义。