海上运动平台多站时差定位算法性能分析

张 亮，姚 力

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

无源时差定位技术(TDOA)是定位站本身不发射电磁波，通过处理多个定位站接收到的目标辐射源信号到达时间对目标进行定位。对目标的二维定位至少需要2个时间差即3个定位站，同理对目标的三维定位至少需要4个定位站，目标辐射源信号到达2个定位站的时间差乘以光速即为辐射源到2个定位站的距离差。在几何上，由“到两固定点的距离差等于定长的点轨迹为双曲线”的原理可知，目标位于以这2个定位站为焦点的双曲线其中一支上[1]。在二维平面内，3个定位站形成的2个单边双曲线的交点就是目标辐射源的位置；同样道理，在三维空间中，4个定位站可形成3对单边双曲面，3对单边双曲面的交点即为目标位置。

在获得TDOA测量值的基础上，由多个TDOA测量值组成1组双曲线方程，求解该方程组就可以得到目标的位置；但是因为该定位方程不是线性的，所以求解存在一定难度。很多文献对时差定位算法进行了研究，已经探究出多种不同的算法，这些算法大多是在目标二维定位的基础上进行推导的，可以很容易推广到目标三维定位的情况。本文将在目标二维定位情况下对一些经典定位算法逐一进行分析。

1 理论分析

三站时差定位示意图如图1所示。

图1 三站时差定位示意图

1.1 时差定位原理

图1中，E(x,y)为目标辐射源的位置坐标，主接收站为O(x0,y0)，辅助观测站为A(x1,y1)和B(x2,y2),则定位方程为：

(1)

式中：辐射源与各定位站间的距离用ri表示；电磁波传播速度用c表示；辐射源信号到达主站与各辅站的时间差为Δt0i；目标辐射源到主站与各辅站的距离差用Δri表示。

由式(1)可解得如下方程组：

(2)

利用时差定位系统测得辐射源信号到达主站和各辅站的时间差，在定位站坐标已知的情况下，2个方程2个未知数，求解该非线性方程组即可得目标位置[2]。

1.2 双曲线直接求解法

双曲线直接求解法可以用来对目标直接定位，也可以用作其他迭代算法的初始值，该算法的特点是计算量小、工程上易实现[3]。

如图2所示，设tO,tA,tB分别为辐射源E(x,y)的同一脉冲前沿到达站O(x0，y0)、站A(x1,y1)、站B(x2,y2)的时间，c为电磁波的传播速度。

图2 辐射源与各站位置关系示意图

令tOA,tOB分别表示同一辐射源脉冲到达主站与辅站A、B的时间差，则有：

(3)

由式(2)可得双曲线方程组：

(4)

将式(4)化成极坐标形式，可得到：

(5)

(6)

解出ρ和θ，得到时差定位解：

(7)

1.3 Chan算法[4]

Chan算法即Chan氏算法，是一种基于TDOA技术、具有解析表达式解的定位算法，是求解定位方程组的一种非迭代算法。它具有计算量小、定位精度高、工程易实现等优点。

对于式(1)所示方程组，整理化简可得到：

(x0-xi)x+(y0-yi)y=ki-r0·Δri，i=1,2

(8)

(9)

为了求解式(8)，将r0看作已知量，由此可得矩阵表达式如下：

AX=F

(10)

对于二维三站定位系统，只要3个定位站不在同一直线上，即：

(11)

满足式(11)时，可对式(10)用伪逆法求得X的最小二乘解为：

(12)

定义矩阵B，使得：

(13)

则方程组(8)的解为：

(14)

(15)

(16)

(17)

当3个观测站坐标满足条件：

y=ax+b

(18)

即当直线布站时，则式(10)中矩阵A为：

(19)

由式(19)可见，A为奇异矩阵，因此上述方法不适用。此时式(8)可化为：

2x0i(x+ay)+2r0ir0=r0i2-ki+k0，i=1,2

(20)

(21)

通常将时差测量误差近似为正态分布的高斯噪声，则测量误差协方差矩阵可表示为：

(22)

为了解方程组(20)，定义：

(23)

(24)

将式(20)看作是关于未知数ω=x+ay和r0的二元一次方程组，解得：

(25)

(26)

由上述推导可知，直线布站时Chan算法的缺点是以噪声近似为零均值正态分布的高斯噪声为前提。在实际测量环境中，该算法的性能将会受到噪声复杂性的影响。

1.4 最大似然定位算法(AML)

时差定位方程是非线性的，最大似然法首先将定位方程变为关于未知数(x,y)的线性方程，该方程的系数也依赖于(x,y)值。在获得定位初始值的基础上，AML算法解方程获取新的定位值，更新方程系数[5]。进行多次迭代，利用最大似然法检验每次获取(x,y)的代价函数，选出代价函数最小时对应的(x,y)作为最终定位值。

1.5 其他定位算法

除了上面推导的3种解法外，时差定位方程的求解算法还有泰勒级数展开法、搜索法、Fang法等。泰勒级数展开法中，为了提高算法的收敛概率，需要找到一个与实际目标位置接近的初始估计位置，然而事实上精确的初始估计位置很难得到。此外，该算法还需要利用时差测量值误差的先验信息来求解加权矩阵，因此泰勒级数展开法计算量非常大、解算效率低、不易实现。搜索算法包括粒子群算法、差分进化算法、遗传算法等，它们的推导简单，但是也费时，不适合实时定位系统。Fang算法计算简单明了，但是该算法只适用于未知量个数(辐射源坐标)与时差测量值相同的情况，当有多余的时差测量值时，即存在多个定位站时，Fang算法不能利用多余的测量值来提高定位精度。

2 算法性能分析

利用均方根定位误差(RMSE)对算法性能进行评价：

(27)

式中：(x,y)表示定位测量结果；(xe,ye)表示目标真实位置。

多站时差定位系统定位误差主要由系统测量脉冲信号到达时间误差、站址误差以及目标所处区域决定，在目标相对各站位置变化的条件下，定位误差主要取决于系统测时差误差以及系统测站址误差，因此接下来对于3种定位算法在系统授时误差和测站址误差影响下的定位性能进行仿真分析。

(1) 三角布站

图3 定位误差随站址误差变化图

从图3中可以看出：站址误差在100 m以内时，Chan算法和AML算法的均方根定位误差都比较小，算法性能较好，而双曲线直接求解法误差大，算法性能较差。

在本文所研究的定位系统中，军用北斗定位精度约2～3 m，考虑舰船纵横摇摆等因素，取站址误差典型值10 m。图4为站址误差为10 m时，3种算法对应的均方根定位误差随时差误差的变化曲线。

图4 定位误差随时差误差变化图

从图4可以看出，随着时差误差的增大，AML定位性能的优势十分明显。然而AML算法是迭代算法，运算量极其大，计算速度慢、效率低，而无源定位必须在有限时间内对来自不同平台的辐射源进行快速精确测量、定位，因而AML算法不适合本文所研究系统。同样道理，其他的迭代算法，如最小二乘法等均不能满足要求。另外，随着时间同步技术以及脉冲配对、时差分选技术的发展，时间测量误差可以达到几ns，可以通过仿真观察时差误差在100 ns以内时3种算法的定位性能，如图5所示。

图5 定位误差随时差误差变化曲线

由图5可见，100 ns以内时，Chan算法具有与AML算法相当的定位性能。另外，随着时间同步技术以及脉冲配对、时差分选技术的发展，时间测量误差可以达到几ns，具备AML算法的优势。更重要的是Chan算法不具有迭代运算，几乎不需要存储数据，定位解算速度快、效率高，因此可以满足无源时差定位系统实时性定位的需求。

(2) 直线布站

设主站坐标(0,0)，辅站1坐标(-10e3,0)，辅站2坐标(10e3,0)。目标真实运动轨迹为xe=-20e3∶5 000∶20e3，ye=xe+40e3。

对直线布站时的Chan算法和双曲线直接求解法进行仿真分析，图6为时差测量误差为20 ns、站址误差为0 m∶10 m∶100 m变化时2种算法对应的均方根定位误差的变化。图7为站址误差为10 m时，2种算法对应的均方根定位误差随时差误差的变化曲线。

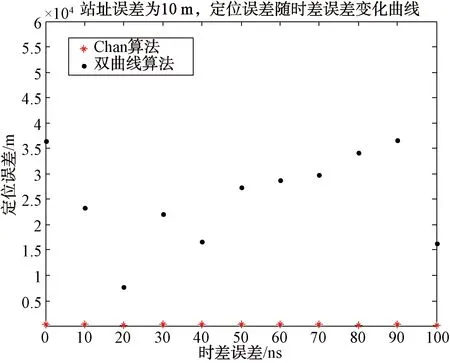
图7 定位误差随时差误差变化曲线

由图6和7可以看出，直线布站时Chan算法同样满足定位精度要求。

图6 定位误差随站址误差变化曲线

3 结束语

综上所述，最大似然法(AML算法)等一系列迭代算法运算量大，耗时较长，效率低，不能满足无源定位在有限时间内对来自不同平台的辐射源进行快速精确测量、定位的要求。在海面上，当海浪很大时，船身摆动幅度较大，存在较大的站址误差，也要考虑不可避免的时差测量误差，在这样的情况下，双曲线直接求解法定位误差大，无法满足高精度的需求，而Chan算法定位精度可以满足需求。另外当存在多余定位站、有多余的TDOA测量值时，Chan算法具有相应的利用这些多余测量值来改善定位精度的解算方法。综合考虑这些因素，海上运动平台多站时差定位系统中选择Chan算法进行定位解算。