基于子结构的宏微结构协同优化方法
2022-12-25吴紫俊肖人彬
吴紫俊 肖人彬
1.武汉纺织大学数字化纺织装备湖北省重点实验室,武汉,430020
2.华中科技大学人工智能与自动化学院,武汉,430074
0 引言
基于子结构方法的宏微结构一体化优化方法中,利用子结构自由度缩减实现了结构宏微观的一体化设计,但需要预先建立不同子结构构型的样本[1],宏观结构优化时只能在预定的微观构型中进行插值,即限制了结构宏微观的优化空间[2]。
宏微结构的协同优化设计是从宏微多个尺度寻找材料的最佳分布位置,组合成不同构型的微观构型和宏观结构,使得材料潜力充分发挥[3]。由于结构设计引入了微观尺度,因而扩大了结构设计空间[4],赋予了结构更多的功能,如最小频率响应的结构[5-6]、具有良好可制造性的宏观结构等[7]。
目前,周期性子结构的优化方法主要有两类[8-9]:基于均匀化方法的周期性结构设计[10-11]与基于宏观结构周期性约束条件的设计方法。在基于均匀化方法[12-13]的周期性结构设计方法中,周期性位移边界条件施加在单胞上[14],并假设结构的应力和应变在宏观结构上是周期性变化的[15-16]。而基于周期性约束的方法中,假设宏观结构中任意两个周期性结构中的单胞具有相同的单元密度和相等的灵敏度值。这两类方法相比,尽管都能获得相近的优化构型,但基于周期性约束条件的设计方法的计算效率要低于均匀化方法。
作为结构拓扑优化的热点分支之一,周期性结构设计得到了许多关注。LI等[17-18]提出基于维度缩减的代理模型来设计周期性结构,降低了结构频率带隙计算的计算资源消耗。ZHENG等[19]基于不确定性负载的高斯分布提出了周期结构鲁棒拓扑优化框架,研究了周期结构设计空间小的结构对不确定性载荷的敏感度。HE等[20]针对不规则有限元网格提出了一种周期性结构优化方法,用非结构设计点来清晰地描述周期结构的拓扑。RIVA等[21]提出了一种基于波在细胞界面反射和传输的纯解析方法,可判断所提出的解决方案的最优性。CHEN等[22]提出了一种用于结构和蜂窝材料拓扑并行设计的移动等值面阈值(moving iso-surface threshold,MIST)方法,利用均匀化理论推导出了宏观结构和微观周期性单元两个维度的物理响应函数。CHENG等[23]研究了周期性均质多孔材料板和均匀加筋实心板的最大面外屈曲载荷设计,并基于渐进均匀化方法和CAI方法建立了结构宏观和微观设计变量与灵敏度分析的关系。DAHLBERG等[24]引入周期性结构单元以获得具有更高对称性的结构,提出利用高对称性设计导频结构,大大减小了低频电波传输时的漏波现象。
赵清海等[25]基于周期性约束提出了多材料结构稳态热传导拓扑优化设计方法,并结合Ordered-RAMP材料插值方法获得了周期性热传导拓扑构型。焦洪宇等[26]利用固体各向同性材料惩罚(solid isotropic material with penalization,SIMP)方法,通过增加周期性约束条件,提出了各向同性微结构材料的周期性拓扑优化方法,并在其随后的研究中[27],对循环对称结构、梯形结构等进行了周期性布局优化研究。杜义贤等[28]利用能量均匀化方法建立了基于宏观力学性能的微观点阵结构的优化模型,以周期性单胞为研究对象,将材料用量和力学方程等作为约束条件,获得了边界清晰的周期性点阵结构;并在其后的研究中[10],结合负泊松比表征吸能特性,提出了兼具吸能和承载特性的周期性宏细观结构多尺度优化方法。
在周期性结构的多尺度设计中,为在设计域中设计微结构构型的同时兼顾微结构在宏观结构中的最优分布[9,29],本文提出了基于子结构法的周期性结构的宏微观设计方法,并利用子结构法中的自由度凝聚来实现周期性单胞的矩阵规模缩减,提高其计算效率的同时,也可利用子结构的反求来完成周期性单胞结构与宏观构型的协同设计。
与此同时,文献[1]和文献[2]中提出的基于自定义微结构构型的宏微结构一体化设计方法ARSP(approximation of reduced substructure with penalization),由于限定了微结构构型的设计范围,其宏观结构与自定义微结构构型之间存在兼容匹配问题。本文为突破预定义微结构构型的设计限制,利用子结构的自由度缩减与反求来实现两个尺度上结构的协同设计,有助于实现大规模个性化设计[30]。
1 子结构与优化插值模型
1.1 子结构凝聚与反求
在优化子结构中,单个子结构的本构方程可表示为[31]
(1)

由式(1)的第二式可得子结构内部节点位移向量:
(2)
将式(2)代入式(1)的第一式,可得方程:
(3)
式(3)可简单表示为
(4)
(5)
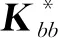
本文中,将利用式(5)进行子结构凝聚组建宏观本构方程的过程称为子结构凝聚,通过凝聚后的本构方程进行结构设计称为宏观结构设计;利用式(2)计算子结构内部自由度的位移的过程称为子结构反求,通过子结构反求获得对应的周期性单胞的过程称为微观结构设计[32]。
1.2 优化插值模型的构建
在周期性宏观结构设计中,假设宏观结构由若干个子结构组成,如图1所示。

图1 周期性子结构与宏观结构
根据子结构可知,宏观结构设计域Ω的计算可直接利用凝聚后的刚度矩阵表示:
KsUs=Fs
(6)
其中,Ks为子结构凝聚后所形成的整体刚度矩阵;Us、Fs为凝聚后子结构交界面上节点的位移向量及载荷列阵。
针对宏观结构设计,设计变量设置为子结构所含的材料体积,由于宏观结构由周期性结构组成,故只需要判断子结构材料的含量。此时宏观子结构材料含量设计变量的取值为(0,1],对应的刚度矩阵可表示为
(7)
其中,ρ为设计变量;p为ρ的惩罚因子。
子结构密度决定了周期性子结构构型的材料含量。微观子结构构型设计中,设计密度为子结构中各个单元的材料含量,利用式(2)可获得子结构的内部节点值,通过优化变量更新即可获得微观结构的构型。假设子结构内部单元的刚度矩阵为K0,它与子结构优化密度变量之间的关系可表示为
Kb=(ρb)qK0
(8)
其中,ρb为该子结构内部单元的材料相对含量;q为ρb的惩罚因子。
2 基于周期性微观单胞的宏微观结构优化
2.1 宏微观优化模型定义
以结构柔度最小为优化目标,实现宏微观结构的协同优化:
(9)
式中,X为宏观结构中所有子结构的密度集合;c为宏观结构柔度设计目标函数;V为宏观结构的材料含量总量;K、U、F分别为整体刚度矩阵、位移场和边界约束;υ为体积约束;ρi为各子结构设计变量;ρmin是为避免奇异问题设定的最小密度,ρmin=0.001。
基于有限元子结构方法,优化问题(式(9))在宏观层面的优化可表示为
(10)

微观结构是构型相同的周期性结构,优化模型可表示为
(11)
式中,cb为子结构柔度优化目标;K0、Uj,i分别为第i个子结构中单元的单元刚度矩阵和位移场;Fbb,i为当前子结构凝聚后的边界自由度对应的位移场;m为当前子结构中单元总数;ρb为微结构构型的设计变量;Vb为当前子结构的体积约束,此时该约束是变动的,与子结构在宏观结构的分布数量相关。
通过上述宏微观的优化模型可知,结合SIMP方法计算,宏观结构的拓扑构型由宏观子结构的材料含量确定。而在微观结构设计中,微观周期性结构设计的材料约束不是固定值,而是根据宏观结构的子结构的材料密度分布进行更新。当宏观结构中周期性子结构分布在整个设计域时,微观结构的材料含量约束与宏观材料约束相同;当周期性结构分布在宏观设计域的子域时,微观结构的材料含量约束将增大。
2.2 宏微观两尺度的灵敏度分析
宏观结构由构型相同的周期性结构组成,假设对式(10)的目标函数计算密度导数:
(12)
微观结构的灵敏度可表示为
(13)
微观上灵敏度与宏观子结构相关,结构优化过程中,在微观结构设计变量增加宏观的惩罚因子项可加快其收敛速度。
在基于子结构的优化方法中,两个维度上的变量更新策略均采用传统的优化准则法(optimality criteria method,OC)[33]:
(14)
在上述更新策略中,ε是变量迭代步长。η=0.5,而优化条件Di可由子结构的目标函数和体积导数定义:
(15)
式中,κ为拉格朗日因子;∂V/∂ρi=vi为每个子结构的体积约束。
2.3 周期性结构的宏微观拓扑优化算法
在该宏微观结构协同优化中,通过子结构自由度凝聚和反求计算,可以获得设计域上所有子结构边界节点和内部节点的位移场。通过式(12)和式(13)计算对应的宏观结构和微观结构的灵敏度。由于微观周期性结构的构型会影响宏观子结构凝聚的刚度矩阵,因此在进行变量更新时,应先更新周期性结构的设计变量,然后更新宏观结构设计变量。对应的优化设计流程如图2所示,关键算法如下所示。

DeginMacroStructure()∥宏观结构设计 while(判断是否收敛) { substrcutureMacro(网格划分参数);∥根据优化参数获得凝聚的子结构有限元模型 calcMacroModel(边界条件);∥计算宏观设计域的有限元模型 for 1:N iSensitivityMacro();∥计算宏观结构每个子结构的设计变量灵敏度 updatingMacro();∥根据灵敏度值更新设计变量 DeginMicroStructure();∥微观结构设计 }DeginMicroStructure()∥微观结构设计

while(判断是否收敛) { for 1:N { calcsubstrcutureMicro(子结构节点编号);∥反求子结构内部节点位移场 iSensitivityMicro();∥计算宏观结构每个子结构的设计变量灵敏度 } updatingMicro();∥根据灵敏度值更新微结构设计变量 }

图2 结构设计流程
该协同优化计算框架中,每一步迭代均会判断宏微观结构是否收敛,而微观结构优化过程中,其材料约束受宏观子结构分布限制,因此,微观结构优化中需要从宏观结构中更新微观材料约束。
3 周期性结构优化实例
3.1 悬臂梁结构的设计(实例1)
以悬臂梁的计算为例,如图3所示,设计域大小为L1×L2=2×1,其左侧固定,右上角承受F=1 N的垂直向下压力。所选用材料的弹性模量为E0=1,泊松比υ0=0.3,体积约束为0.4。Nx与Ny分别是水平与垂直方向上的子结构数目。
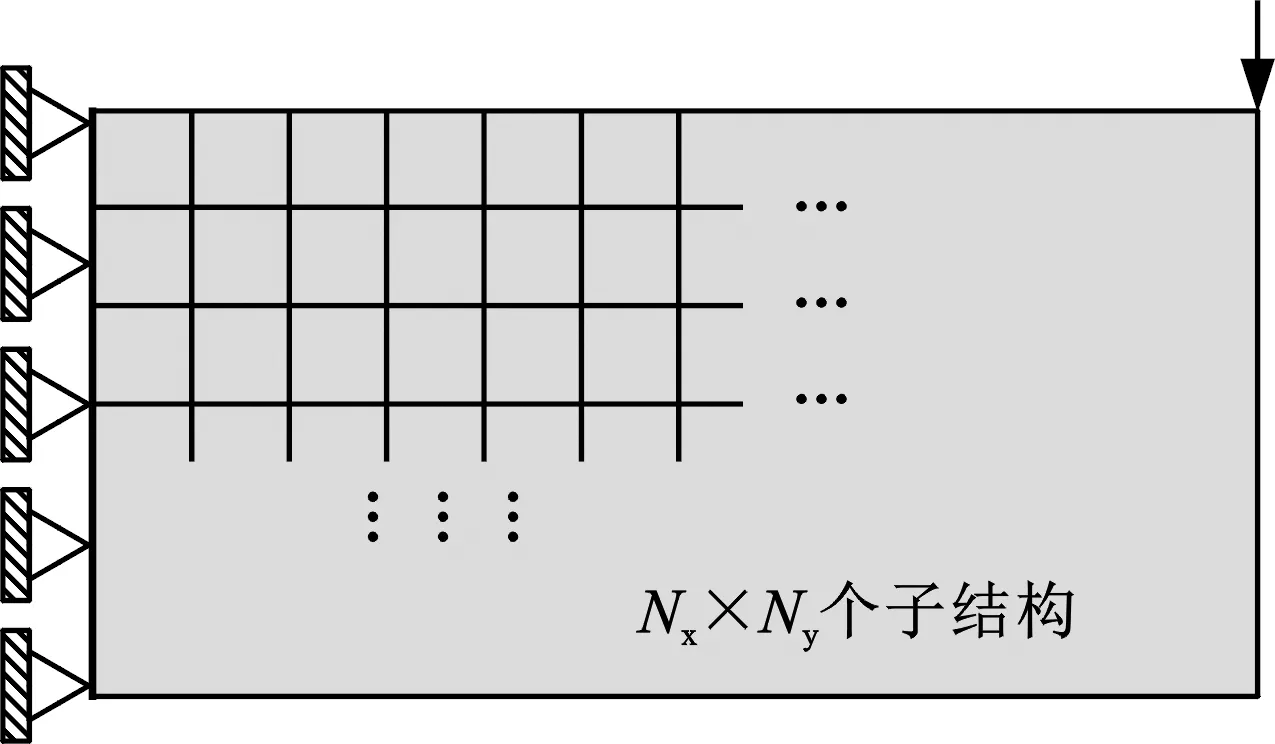
图3 优化模型(实例1)
设计域划分为320×160个四边形平面单元,并选择不同大小的子结构进行宏观结构凝聚。宏观结构设计中,惩罚因子p设置为2,过滤半径设置为与单元边长相等;微观结构设计中,惩罚因子q设置为3,过滤半径设置为1.1。具体参数设置如表2所示。基于SIMP方法,不考虑宏微观协同设计时,该模型的优化构型和柔度值c如图4所示。

表2 宏微观优化设计参数

图4 基于传统SIMP方法的优化设计结构
在不同子结构大小下的优化结果如图5所示。从优化结果可看出,设计域划分的子结构越多则结构杆系特征越明显,随着子结构数量的增多,其宏观结构的柔度值先增大后减小。

(a)Nx×Ny=2×1, (b)Nx×Ny=8×4,c=79.72 c=90.03
微观结构优化过程中,随着宏观结构的杆系特征越来越明显,材料逐渐向微结构中集中,使得微观结构周期性子结构中的材料增多,微结构的杆系特征越来越不明显。
随着设计域中的子结构数量增多,通过式(11)可得出宏观结构的材料会逐渐集中到各个子结构中,使得周期子结构单胞中的材料逐步增多。对比图5c与图5d,宏观结构的杆系特征越明显,材料在子结构单胞中的集中程度越大。由此可以推导出,在利用所提出的周期性子结构设计方法进行结构设计时,需要平衡宏观结构划分和周期子结构单胞大小。
3.2 固端梁的结构优化设计(实例2)
如图6所示的固端梁结构优化问题中,设计域大小为L1×L2=2×1,其左右两侧固定,设计域中心受F=1 N的载荷。宏观结构划分为Nx×Ny=8×4个子结构,子结构大小m×m分别设置为10×10、20×20、30×30、40×40,体积约束为0.3。宏微观优化参数同上一实例。
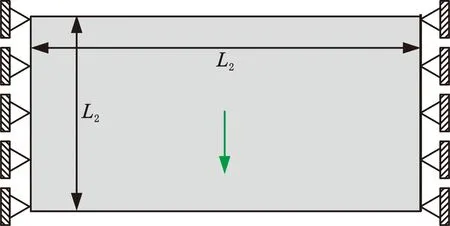
图6 优化模型(实例2)
在不同子结构大小下,该优化模型的设计结果如图7所示。从优化构型来看,宏观结构基本相似,其结构柔度值随着子结构的增大先增大后减小。从微观构型来看,无论子结构尺寸的大小,均可得到相似的微观构型,随着子结构尺寸的增大,构型越来越清晰,其周期性子结构如图8所示。

(a)m×m=10×10, (b)m×m=20×20,c=12.97 c=13.55

(a)m×m=10×10 (b)m×m=20×20
从优化目标函数分析,本文所提的周期性结构设计方法所得结构柔度值均小于ARSP方法[1]所得结构柔度值。相比于ARSP方法,本文方法由于扩展了子结构内部的设计空间,可以得到柔度更小的优化构型。
在宏微观协同优化过程中,由于微观结构优化嵌入到了宏观结构优化中,为了得到清晰的微观构型,微观优化变量迭代步长应小于宏观优化步长,避免迭代步长太大使得微观构型变化剧烈,从而引起宏观优化时的收敛速度缓慢的问题。图7d的优化收敛过程如图9所示。在迭代计算中,最后一步的柔度值有较大程度的减小,这是由于在该迭代步的前一步已经得到了最优构型,即该迭代步不属于优化过程的迭代步,而是为了获得优化构型的实际柔度值,通过有限元方法进行结构的直接计算,即惩罚因子设置为1时获得的结构柔度值。通过SIMP方法,在整个优化过程中宏观材料含量不变,其材料在微观周期性单胞构型和宏观周期性结构分布之间进行匹配,以同时获得宏微观构型。

图9 图7d的收敛过程
对比上述两个实例,为了避免由于宏观子结构数增多而导致的周期性子结构大小减小,进而导致材料在周期性子结构中过度集中,难以获得具有明显几何特征的周期性子结构,在利用所提方法进行周期性宏微观结构设计时,尽量采用固定周期性子结构单胞大小的形式进行优化计算,既可获得清晰的宏观构型,又可避免由于材料集中引起的周期子结构单胞结构特征不清晰的问题。
4 结论
本文提出了基于子结构法的周期性微观构型的宏微观协同设计方法,根据子结构凝聚和反求构建对应的宏微观优化模型。基于SIMP方法的优化框架,利用子结构的自由度凝聚实现结构的宏观构型设计,利用子结构内部自由度反求来实现周期性微观构型设计,同时给出了该优化方法的灵敏度计算和变量更新迭代方法。通过两个实例验证了所提方法的合理性。
相比于传统基于均匀化的宏微观协同优化方法,基于子结构的宏微观协同优化方法可利用子结构及其对应超单元实现宏观结构的快速迭代和微观结构的再设计。由于子结构是宏观设计域的一部分,网格、节点等是一一对应的,故解决了均匀化方法的尺度分离问题。同时通过子结构自由度凝聚提高了宏观结构的设计效率。
尽管本文基于子结构实现了周期性结构的宏微观协同设计,但仍然存在以下几个问题,需要进一步研究。一是优化效率需要进一步研究。通过构建子优化问题实现微观周期性结构的设计,子结构划分的网格数越多,则微结构构型越精细,但也制约着整个优化问题的计算效率。二是宏微观设计参数的匹配仍需要进一步研究。较大的迭代步长会加快结构设计的收敛速度,本文中宏观结构与微结构通过两个关联的优化问题分别设计,较小的子结构设计变量迭代步长将影响宏观结构的收敛,较大的宏观设计变量迭代步长可能会让子结构得不到合适的微观构型。
