初中数学教学中纠错原则、时机与方法的探究
2022-12-25杨小璐
杨小璐
江苏省南通西藏民族中学 226001
心理学家R.Bainbridge认为:差错每个学生都有,教师若不加以利用是不可原谅的.错误是学习者攀上正确结论宝座的台阶,利用错误引导学生步入正轨是每个教师的基本职责[1].实践证明,数学纠错教学需要遵循一定的原则与方法,学生在纠错过程中能不断优化思维,形成系统的认知结构,为培养自身的辩证思维能力奠定坚实的基础.
纠错教学应遵循的原则
(一)目的性原则
错误产生的原因有多种,分别有教师、学生方面的问题,还有教学环境对学习产生的影响等.其中,最主要的错误原因集中在学生层面,有智力与非智力两大因素.从错误的认知结构角度来区分,存在知识性、策略性、心理性与逻辑性等错误;从错误的表现形式来看,错误发生的原因有审题、运算、方法、运算或表述欠规范等.
人们常说的纠错,主要是针对学生认知结构方面的错误而言.作为教师,首先要明确学生错误发生的原因,并在此基础上明确教学目标,此目标包括认知目标、情感目标以及智能目标等,且目标不宜过高或过多.
(二)针对性原则
每个学生受认知经验的影响,所产生的错误类型各不一样.纠错之前,教师应根据错误类型,有针对性地对普遍性错误、抽象晦涩的错误以及解题方法错误等进行纠错教学.同时还要搜集、整理学生的典型错误,重点明确地、有针对性地进行讲解,以突出问题的本质.切不可尝试面面俱到地讲解,那只会浪费课堂宝贵的时间,降低学习效率.
(三)主体性原则
学生是课堂的主人,纠错课亦如此.教师在纠错教学时,应突出学生的主体地位,创设丰富的教学情境,运用学生感兴趣的教学手段,引导全体学生积极地参与到纠错中来.而教师应充当引导者的角色,在学生自主探究过程中,教师可在学生知识的生长点处加以启发、引导与点拨,鼓励学生自主发现错误的根源,从而找出解决问题的关键.或者鼓励学生采用分组讨论的方式,在取长补短中发现学生思维的偏差点,及时纠正错误,实现思维的突破.
(四)巩固性原则
实践证明,缺乏练习的纠错效果很差,往往隔几天学生同样的错误又会死灰复燃.反馈练习是克服这个问题的主要手段,这里所说的反馈练习不仅仅是巩固练习,还包括变式拓展,学生只有从根本上掌握数学思想方法与解题技巧,才能实现真正意义上的纠错.
纠错教学应遵循的时机
(一)及时
纠错讲究时效性.学生新知建构时所发生的错误,如概念、定理等的理解偏差或方法理解错误等问题,及时进行纠正,往往能起到良好的效果;学生的一些无意识错误,表现比较隐匿,常常不会自主发现,如运算过程中的格式不规范等问题,若教师能给予及时引导与纠正,往往能起到良好的效果[2].
例1一部分学生,总是搞不清楚以下几种说法所表达的真实意义:①x,y的平方差;②x,y的差的平方;③x,y的平方的差.
从字面来看,这三种表达方式非常接近,难怪学生会混淆不清.为了清除学生学习道路上的障碍,教师应及时引导学生对这几种表达方式进行辨别,只有从根本上弄清其所表达的意思,才能保证解题时不出现差错.
如平方差公式的应用,一些学生对这个知识点模糊不清,看到问题就生搬硬套,从而导致(-x+y)(x+y)=x2-y2错误的发生;还有学生将完全平方公式理解成(a+b)2=a2+b2.面对这些错误,教师应及时矫正学生的认知结构,避免学生将错误的内容建构到认知中,形成不良记忆,为后续解题带来隐患.
(二)延后
面对下面两类问题,教师可采取延后纠错的方式:一是对学生整体数学思维与解题思路影响较小,对主体教学过程不会引起重大冲突的错误.若即时纠正,则会打断学生的解题思路,影响学生对问题的全局性理解;二是典型错误,具有显著的代表性,需要重点强调、系统讲解的错误.
例2解方程(x+2)(x-1)=2+x.
错误:学生将方程的两边同时除以“2+x”,解得x=2的结论.
这是一个典型的错误类型,很多学生在初次接触此类运算时,都会犯这样的错.同时,本题对接下来的课堂讲解不会造成不良影响.为此,笔者采取延后的方式,带领学生针对此类问题进行启发式的纠错,以帮助学生形成正确的解题方式.
师:解本题时一些学生想到了用“约公因式”的解题方法,就在方程的两边同时除以“2+x”这个式子,并获得了x=2的结论,你们觉得这种解题方法对吗?
生1(语气不够肯定):好像不对.
师:你们觉得哪里不对?大胆地说出你们的看法,错了也没有关系,让我们一起来探讨这个问题.
(学生沉思)
生2:“2+x”中含有未知数,我们还不知道它的取值,直接用来运算,好像不合理.
师:没错!在方程的两边同时除以一个包含未知数的代数式,运算后所得的方程和原方程不一定是同解.因此这样的变形方式存在失根的情况.
(学生有所感悟)
生3:我是不是可以将本题的错误理解为:解题中因除掉了“x=-2”这个因子,致使失根的情况?
生4:对的.因此我们遇到解此类方程的问题,不能将一个代数式作为除的对象,还是要先移项,再进行因式分解,在降低方程次数的情况下解方程,才能避免出现失根的现象.
师:总结得非常好.本题出现错误的关键在于除以了代数式“2+x”,以后我们遇到此类问题要避免出现这样的错误.本题除了以上解题方法之外,还存在其他的解题方法吗?
(学生思考)
生5:如果我想坚持在等式的两边同时除以“2+x”,有没有办法解题?
学生们都觉得不可思议,这不是刚刚被否定掉的解题方法吗?教室里传来了窃窃私语.
生6:如果要从这条思路去解题的话,首先要确保“2+x”的值不为零.
生7:问题是题设条件中并没有明确表示“2+x”不为零呀,而且当“2+x”的值为零时,该方程也是成立的.
在这两位学生的交流中,不少学生恍然大悟,提出用分类讨论的方式来解决.
师:应该怎么分类呢?
生8:自然是以2+x=0与2+x≠0两种方式来分类.
……
通过教师的点拨与学生的自主探究,本题获得了不同的解决方法.回过头来看,延后纠错从本质上来看,就是让学生围绕某个特定的错误,给予学生充足的探讨与反思空间,让学生在一定的范围内进行探索研究的过程.延后纠错的方式更符合学生的认知发展规律,可以让学生的思维在探索中得到有效提升.同时,学生的思维之门被打开,常会得到意想不到的收获.因此,延后纠错法是初中数学纠错教学的重要手段之一.
纠错教学应遵循的方式
(一)自纠
学习过程中,有些错误是学生常会犯的.作为教师,要做到心中有数,对于学生常犯的一些典型错误,可鼓励学生与同伴多交流,及时发现错误,从而自主纠正.如何培养学生的自主纠错能力是笔者经常思考的问题.实践证明,教学过程中将正确的检查方法渗透给学生,对学生自主发现错误具有重要作用.不论遇到什么问题,教师要引导学生认真读题、审题,及时发现问题中的关键信息,这样能避免错误的发生.
例3已知关于x的方程(m2-4)x2+2(1+m)x+1=0有实根,求m的取值范围.
本题是一道常规题,难度系数并不大,但学生在解题中总会出现错误.为此,笔者特邀请两位成绩中等的学生到黑板上演示解题过程,以供大家讨论.
生1:题设条件明确提出此方程有实根,那么可确定Δ=[2(1+m)]2-4(m2-4)=20+8m≥0,可得m≥-,由此可知本一元二次方程中m的取值范围为≥-
师:请同学们重新审题,看看本题有没有什么隐含条件,或者被我们忽略的东西呢?
(学生重新审题)
生2:本题并未明确表示该方程是一个一元二次方程.
师:哦?遇到这种情况,我们该怎么处理呢?
生3:需要分类讨论,才能回答完整.
师:本题该从什么角度进行分类讨论呢?
生4:可分为m2-4=0与m2-4≠0两种情况进行讨论.
……
随着教师的引导,学生在解题过程中不仅发现了错误的原因,还自主找到了解决问题的具体办法.这种教学模式,不仅能有效地提升学生的纠错能力,还能有效地发展学生的思维,为学生的辩证思维能力的形成奠定基础.
(二)他纠
学生因年龄特征与生活经验的相似性,对问题的看法常存在一定的共性.当学生对概念、定理或公式的理解出现偏差时,教师可引导学生观察同伴的解题过程,并针对同伴所呈现的方法与结论谈谈自己的看法,这样能让学生从其他学生身上看到自己的影子,不仅能纠正别人的错误,还能有效地提高自己的洞察力[3].同时,学生可取长补短、查漏补缺,避免别人的错误在自己身上发生.
例4如图1,已知正方形ABCD的边长是4,点P为BC边上的一个动点,且QP与AP为垂直的关系,交CD于点Q,假设PB=x,△DQA的面积是y.
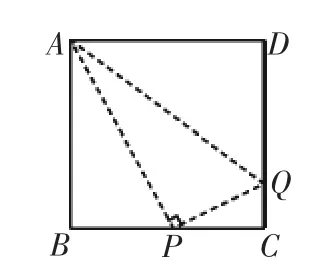
图1
(1)求x,y之间存在怎样的函数关系,列式表达;
(2)求点P位于何位置,△DQA的面积值最大?
在学生解完题后,教师并没有马上呈现正确答案,也没有进行讲评,而是要求同桌之间互相查看对方的答案与自己的答案是否有差异.在同学的交流过程中,不少学生发现同伴出现了以下的错误解题方式:
错解:(1)y=x2-2x+8;(2)根据y=x2-2x+8,解得(x-2)2+6,因此在x=2时,△DQA的面积最大为6.
观察发现,班上有好几名学生都发生了类似的错误.为了让学生记住正确的解题方法,教师鼓励学生以小组合作的方式来讨论本题,由小组长与同学一起分析错因,小组成员一起探寻正确的解题方法.
巡视过程中,教师听到如下交流:观察图1,如果点P的位置恰巧在点B处,点Q 的位置就位于点C 处,那么此时△DQA的面积与△ABC的面积则相等,为8.显然大于以上所求得的6,因此这种解题方法肯定是不对的.
通过交流,学生得到以下结论:本题在解第二问时,特别容易出现两个错误,分别是:①将最小值理解为最大值;②认为所求面积只存在最小值,没有最大值.而出现这些问题的根本原因就在于解题过程中,点P的限制条件被忽略了.
随着互相纠错法的应用,学生对此知识点产生了深刻的认识,这比教师拼尽全力地讲解效果来得直接、明显.他纠的方式,一般适用于错误比较单一,学生容易理解的错误中.学生在互相纠错的过程中,不仅体验到学习带来的乐趣,还有效地培养了学生的观察能力与思维能力.
(三)师纠
有些错误的发生呈群体性,且错误的成因特别混乱、复杂,自纠与他纠无法达到良好的效果.遇到这种情况,就要发挥教师的作用了.教师首先要分析错误发生的原因、学生的认知水平以及预期的教学效果等,做到知此知彼,才能百战不殆.有时,反例法的点拨,能开阔学生的视野,让学生彻底告别混乱不清的思绪.
例5如图2,已知∠ABD=∠BCA,∠ABC=∠D.不少学生根据这两个条件,就确定△ABD≌△ACB.面对这个错误,教师首先应分析学生形成这个错误的原因,并根据学生的认知结构,在归因后采取一定的教学手段进行纠错.
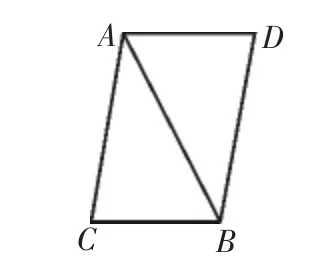
图2
学生所提到的这两个三角形并非是全等的关系,因为△ABC中所涉及的AB边与△ABD中的AB边并非为对应的两条边.
与之类似的还有一些学生,将两个三角形中两条边和一对角对应相等的情况,判断为这两个三角形为全等关系.以上错误都是学生对概念的理解不够清晰引起的,在遇到解决实际问题时,就会出现知识的混乱,觉得差不多就给予判断,从而导致错误的发生.遇到此类情况,教师应带领学生回过头来将基础的概念、定理等重新分析、解读,帮助学生实现知识的重构.
总之,错误并不可怕,只要教师用正确的态度去面对错误,充分挖掘与利用错误资源,那么错误就是宝贵的、有价值的教学资源.教师从心理学角度出发,利用错误在学生心中形成的落差效应,抓住契机,用适当的方式给学生带来认知上的震撼与冲击,往往能起到良好的纠错效果.
