重组知识结构，联系生活实际——以“等腰三角形”的教学为例

盛茂岳

甘肃省武威市凉州区皇台九年制学校 733000

等腰三角形是轴对称图形的直观展示，是几何图形学习中的关键知识点，研究等腰三角形的教学对于几何中的边角关系的教学能起到非常重要的作用.在学习等腰三角形的基础上，学生会对几何图形的性质和判定有比较深刻的理解，为接下来学习等边三角形、线段相等、角相等等几何问题的证明奠定了基础.笔者从联系生活实际、整合知识结构和深度学习的角度，谈一谈“等腰三角形”的教学，供大家参考！

重组教材知识，探究本质规律

等腰三角形作为三角形的一种特殊表现形式，与一般三角形既有联系，又有区别.它具有一般三角形的边和角的特征，同时还有其特殊的轴对称的性质.因此在研究等腰三角形时，除了可以通过三角形的全等知识进行探究以外，还需要从轴对称的角度进行研究.这就要求在教学中教师要进行教材知识点的整合，将几何图形的相关知识点综合运用，从中分析等腰三角形的本质特征.利用轴对称图形的特点可以探究等腰三角形的相关性质，同时也能在以后的几何证明中利用三角形全等的相关特性进行几何证明.

探究活动1：

活动准备：学生分组、直尺、剪刀、长方形纸片.

活动过程：学生利用准备的工具剪出一个等腰三角形.

活动结果：学生展示自己实践的结果，并说明其原理.

设计意图通过学生的动手实践，引导学生理解通过对折三角形的方式进行剪裁，剪出了等腰三角形，这是利用了等腰三角形区别于一般三角形的性质，而折出的这条线就构成了三角形的左右对称（如图1）.

图1

探究活动2：等腰三角形的性质和定理

师：请同学们在刚才剪出来的等腰三角形上标出A，B，C，D，如图2，然后再将这个三角形进行对折，同学们发现了什么？

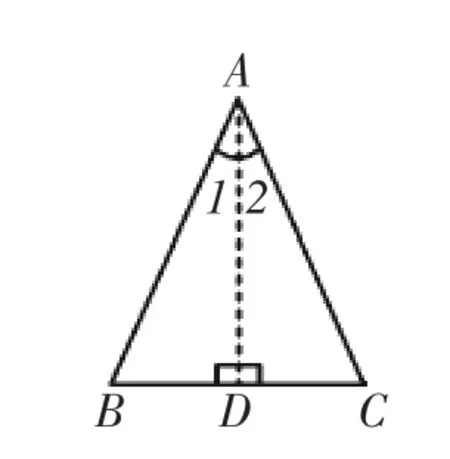
图2

生1：通过对折发现等腰三角形不仅轴对称，而且它的两个底角还相等.

师：很好，这就告诉我们一个定理“等边对等角”.我们如图作一条辅助线AD，同学们仔细观察图2，还能发现哪些相等的边和角呢？

生2：我发现图上的∠1和∠2相等.

生3：BD和CD相等.

生4：线段AD不仅是等腰三角形的对称轴，还是三角形的高.

师：通过刚才同学们的观察，我们发现AD既是∠A的角平分线，还是三角形的高，也是三角形底边的中线，所以也就是“三线合一”.

本例教学时教师设计了学生的动手实践活动，在动手操作和观察分析中，进行问题引导，利用轴对称图形的特性研究等腰三角形的性质，通过折叠、作辅助线等形式，进一步研究等腰三角形的“三线合一”的特点，在过程中渗透几何证明的方法.这样的教学活动相比于教师直接讲授来得更加直观，学生不仅锻炼了动手实践能力，还能在观察分析中提升思维能力，初步掌握几何图形的学习方法.

贴近生活实际，灵活解决问题

数学来源于生活，最终又应用于生活，数学中的几何知识在生活中的应用则更加普遍，因此几何图形的学习可以和生活紧密结合，用来解决实际问题，提高学生运用知识的技能.几何图形在生活中出现的场景很多，教师可以利用多媒体展示图片和场景，可以展示一些特色的建筑，比如北京鸟巢、上海世博会场馆图片.这立刻点燃了学生的学习热情，让学生感觉到生活中到处都有数学知识的运用.在展示过程中，教师可以结合图片引导学生认识等腰三角形的底边、腰、顶角及底角等，认识等腰三角形的各个要素，为进一步的研究打下基础.

案例等腰三角形的应用

如图3，在民族特色民居中，许多房子的顶都是一个等腰三角形，在搭建房子顶时，AB和AC相等，柱子AD与BC垂直，已知BC等于6，∠BAC是120°，求∠B是多少度，BD的长度是多少？

图3

本例从实际问题出发，考查学生对于等腰三角形“三线合一”定理的认识，符合学生的认知特点，既激发了学生的学习兴趣，也渗透了数学的建模思想，培养了学生运用知识解决实际问题的能力.在此基础上引导学生进一步思考等腰三角形“三线合一”的定理在实际生活中的运用，如在修建等腰三角形的屋顶时，通常会从屋顶的顶点系一个重物，往下挂，系重物的绳索要恰好经过一个关键点，那就是三角形的底边中点.请学生思考这么做的理由，讨论利用等腰三角形的定理解释这么做可以保证房屋屋顶的水平.

从现实生活的图形中抽象出基本的几何图形，进而利用图形的性质解决问题，将所学知识应用到生活实际中去，体现了由具体到抽象再到具体的思维过程，有利于培养学生应用知识的能力，帮助学生体会生活，理解数学.

在实际问题的运用过程中，体现了学生对于知识的调动和运用技能，既能达到巩固知识点的作用，又能在解题中利用数学建模思想解决实际问题，培养学生运用知识的技能，感受数学的实用性，体会数学的魅力.

精心组织训练，渗透解题思想

等腰三角形的教学除了基础的性质和定理以外，更重要的是要渗透数学的思想和方法，让学生由感性认识上升到理性认识，能对具体内容进行概括和归纳.教师要通过具体的习题进行巩固和检测，在例题训练中逐渐渗透思想方法.在习题训练的设计中，教师应精心挑选能反映等腰三角形典型性质的习题，通过典型例题的训练，使学生能加深对解题思路的理解.

习题训练1如图4，三角形ABC中，AB 和AC 相等，点D 是底边BC 上的一点，已知AD和BD相等，求证∠ADB和∠BAC相等.

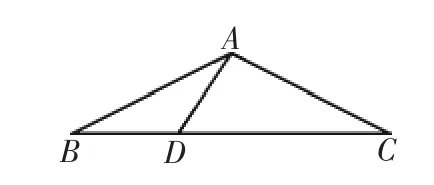
图4

本题在引导学生解题时要渗透数形结合的思想，利用等腰三角形的边和角的性质，通过数形结合的思想将数学的语言转化为文字关系，将知识点进行联系，充分联想构建等量关系，利用数量转化进行求解.在问题探究中，通过数形结合方法的使用，大大提升了思维的深度，使学生将数学知识内化为对数学思想的认知，训练了学生的思维.

在习题训练中，还可以通过“一题多解”的试题，训练学生思维的发散性，让学生能充分理解等腰三角形的性质.

习题训练2“一题多解”

如图5，已知三角形ABC中，AB和AC相等，点D和点E在线段BC上，并且AD和AE相等，求证BD和CE相等.

图5

本例是一道一题多解的试题，着重训练学生对等腰三角形性质的灵活运用，在引导学生小组讨论、自主思考的基础上，教师要引导学生采用多个角度进行解答，如可以通过等量转换、构造的思想，可以通过作辅助线的方法（如作顶角的角平分线、作底边上的高等）进行解答.在探究多种解法的过程中，让学生进行深度思考，不仅加深了学生对等腰三角形性质的印象，而且可以让学生寻找最佳解题途径，培养了学生的创造性思维.

数学课堂中数学思维的培养至关重要，它是学生能够提升综合素质的关键.在数学思维的培养中，教师要注重引导学生体会数学活动的过程，在数学知识发生发展的过程中逐步掌握数学思想和数学方法，真正形成自己对数学的认识.教师要通过对教材知识点的理解、整合，利用生活中数学问题的转化和优秀的习题训练，加强学生对知识的理解，在问题引导和设问启发中发展学生的思维，培养学生的创新意识.

总之，教师对课标、教材的理解，对数学方法和思想的把握，都会在一举一动中潜移默化地传授给学生.因此教师要提升学生的核心素养，就要不断提升自己的专业知识水平和教学能力，做一个终身学习者，才能长久地影响学生，促进学生的全面和可持续发展.