数学猜想：拓展学生思维的有效方法

薛丽雅

江苏省江阴市华西实验学校 214421

数学猜想是数学学习过程中的一种重要方法，许多重要的数学理论的诞生都来自于数学的猜想.在数学课堂上，教师引导学生进行数学猜想能让学生调动思维进行思考和参与学习活动，既是学生对知识掌握情况的反映，也是学生积极学习的情感体现，因此有效利用猜想的教学方法，可以提高课堂教学效率.然而猜想不是空想，是学生在教师创设的情境下有方向地推测和判断，是基于学生已有知识作出的合理猜测，有效的数学猜想可以推动数学问题的解决，促进课堂的有效生成.

几何学习的过程中数学猜想的教学方法尤为重要，因为几何证明需要经历直观几何到实验几何再到论证几何的过程，数学猜想可以在已知条件和结论之间建立联系，促进学生直观思维的形成，更快地找到问题的突破点，增强学生学习的信心.笔者以“直角三角形的性质”一课为例，尝试采用“数学猜想”的教学方法，引导学生根据直观经验进行猜想，进而采用数学理论加以证明的方法，来学习直角三角形的性质定理.

教学案例

（一）导入教学

1.课前准备

操作①：准备一张纸片，将其剪成直角三角形的形状.

师：请同学们谈一谈采用什么方法准备这个直角三角形纸片的？

（学生畅所欲言）

师：想一想可以从哪些方面认识一个几何图形，如边、角、线段等？

操作②：在教师的指导下，学生跟随几何画板的演示进行操作，如图1，将直角三角形纸片进行翻折.

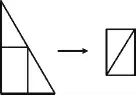
图1

师：通过刚才的实验操作，你发现直角三角形具备其他图形所没有的特点了吗？

2.探索直角三角形的性质1

（1）从“角”上观察直角三角形的两个锐角翻折后与直角相重合，探讨直角三角形“角”的特性.

（2）进行猜想并证明：直角三角形中两个锐角的关系.

（3）定理1的简单运用：如图2，在已知直角△ABC中，∠ACB是直角，若斜边AB上的高是CD，图中有几对相等的锐角和几对互余的角？

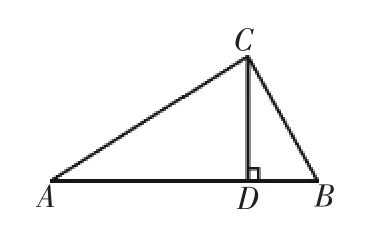
图2

3.探索直角三角形性质2

（1）根据操作②，请你猜想一下直角三角形的线段有什么特殊性？

（2）猜想：在直角三角形中，斜边与斜边上的中线具有倍数的数量关系.

（3）学生思考讨论之后，小组交流证明方法.

（4）如图3，学生展示出两种证明方法，教师进行点评.

图3

教学反思

通过实验操作引导学生关注“直角三角形纸片”，起到温故知新的作用，既能复习直角三角形的概念，又为进一步学习直角三角形的特征奠定基础，激发学生对新知探究的好奇心.接下来通过实践操作，师生共同研究直角三角形的性质，了解直角三角形的角、边的特殊性，为启发学生猜想指明正确的方向.在教学环节的设计中，通过实践操作引导学生进行直观地观察，进而引入下一环节的猜想和证明.

教学设计 “探索直角三角形性质1”时，学生已经通过观察得到直角三角形的“角的特性”，理解了直角三角形两个锐角具有互余的关系，结合导入环节中直角三角形的定义为论证明确了方向.定理1的运用已经关注到直角三角形的特殊线段，让学生认识到直角三角形斜边上的高可以将一个直角三角形分为两个直角三角形，为后续探究直角三角形斜边上的中线特殊性打下了基础.

“探索直角三角形性质2”时，通过再次观察操作实验，经历联系、类比到证明的过程，让学生学会研究问题的思维方法，体会数学之美，感受成功的喜悦.

通过这个翻折实验，既复习了直角三角形的概念，又使学生通过观察判断出直角三角形中角的特性，并渗透了类比联想的数学方法，可谓一举多得.

猜想教学的策略

在几何问题的教学中，教师让学生以问题为导向进行猜想，可以使学生学好直观几何和实验几何的基础上，为论证几何问题打好基础.但是学习目标达成的基础是让学习真正发生，因此猜想不能流于形式，不能无目的地随意猜想.猜想并不是为了活跃课堂气氛的随意操作，更不是为了“猜想”而“猜想”.

（一）让猜想为新知的学习助力

在新知学习的起步阶段，猜想可以活跃课堂气氛，激发学生的学习动机.猜想能在学生已有知识经验的基础上，架起与未知的桥梁，让学生更快地进入新知的学习状态.在讲授 “勾股定理”的知识时，笔者尝试了如下的设计：

1.教师利用多媒体展示动态虚拟模型：以直角三角形的三条边为边长向外作三个小正方形，向正方形中注满液体，其中两个小正方形中的液体正好可以注满一个大正方形.这样的动态演示可以激发学生的好奇心和对直角三角形特殊性的探究欲望.

2.设计实验操作的动手题，学生自己动手画出一个直角三角形，通过测量斜边的长度检验自己的猜想是否正确.经过测量，学生发现自己的猜想是正确的，更加激发了用理论进行证明的积极性，教师适时地渗透数学方法进行引导，能帮助学生朝着正确的方向进行论证.为了激发学生的兴趣，教师还可以进行数学史的讲解，利用《周髀算经》中关于勾股定理的知识进行渗透，调动学生的学习热情.

3.教师引导学生在研究特殊例子的基础上，进一步总结一般规律，并利用统计数据验证猜想，用几何理论进行证明.

（二）让猜想在学习的过程中提升思维品质

猜想是学习过程中的“催化剂”，可以为学习助力，促进学生多角度思维的生成，使学生能够透过现象抓住事物的本质，加速大脑中表象形成的速度.笔者在教学“直角三角形的性质定理2”时，让学生进行了如下的探索实践：

1.如图4，在直角△ABC 和直角△ACE中，∠ABC和∠AEC都是直角，AC的中点是点M，连接BM，EM和BE，BE的中点是点N，你能猜想MN和BE的位置关系吗？

图4

2.如图5，若直角△ABC 和直角△ACE在直线AC的同侧，MN和BE的位置关系有变化吗？

3.如图6，在△ABC中，BD是AC边上的高，CE是AB边上的高，点M是BC的中点，点N是DE的中点，在上述图形中哪两条线段有特殊的位置关系呢？

图6

通过一组猜想活动，在图形变化的变式训练中，学生可以通过不同的图形认识到这一组题的解题思路都是一样的，从而体会数学的化归思想.一组连续的猜想和设问可以激发学生学习的动力，调动学生的积极情绪，使学生处于兴奋状态，提高学习效率.经过不断的猜想、论证，再次猜想、再次论证的循环反复过程，使学生对这一知识的认识由模糊到清晰，逐渐深入理解，最终掌握学习的方法.

（三）让猜想在知识建构之后保持学习的热情

在完成了新知的学习之后，教师可以让学生继续猜想，猜一猜接下来会继续学习什么内容，今天所学的内容可以应用到哪些问题当中，让课堂上学习的热情延续到课后，继续扩大学习的成果.笔者在“直角三角形性质”这节课的最后，进行了如下的总结：

师：同学们，今天我们研究直角三角形的性质，主要是从哪些角度进行研究的？

生：我们通过两次探索，第一次是探索直角三角形的角，第二次是探索直角三角形的特殊线段.

师：非常好！那么我们还能从哪些角度进行研究呢？

生：还可以从直角三角形的边进行研究.

师：是的，三角形的构成要素中还有一项重要内容是三角形的边，直角三角形边的特殊性正是我们下一节课需要探究的内容，同学们可以提前思考……

综上所述，数学猜想是研究数学问题的重要方法，学生在经历实验观察到猜想论证的过程中，培养了自己的观察分析能力和思考探究能力，调动了多重思维的综合运用，从“学会”走向了“会学”.在日常的教学中，教师要搭建学生猜想的平台，给学生足够的思考空间和时间，激励学生参与到数学的学习活动中来，能逐步学会运用观察、实验、猜想、论证的学习方法，提升几何学习的有效性.在探究的过程中，不仅让学生学习知识，而且进行情感的体验，真正成为善于学习、乐于学习的人.