“点线式”教学法的实践与反思
——以“中心对称”的教学为例
2022-12-25李婧
李 婧
福建省厦门市禾山中学 361000
同一教学内容,教学设计不同,教学方法不同,产生的教育价值也会迥然不 同[1].基于此,数学教师要勇于开拓创新,以提升学生的核心素养为出发点,打造主旨鲜明的课堂教学新思路.笔者在执教“中心对称”一课时,使用了“点线式”教学法,取得了良好的效果,现将探索与感悟与大家分享.
关于“点线式”教学法的概述
“点线式”教学法的“点”指基本的概念公式、法则定理、基本模型等,“线”指知识点之间、基本问题之间的相互联系、相互作用.其中“点”是问题的根本所在,“线” 是贯穿问题的思想脉络.“点线式”教学法有两种形式:第一种是将问题横向联系与变式,寻求同类问题之间的互相联系,以发展学生思维的广阔性;第二种是将问题纵向联系与剖析,再将问题拆分为几个小问题,或分解为几个步骤加以解决,以促进学生思维的深入发展[2].
对“中心对称”的教学,立足于新课程标准,笔者以“点线式”教学法为指导,以“问题情境—数学抽象—模型应用”为路径尝试进行教学实践,在活动探究中引导学生经历观察、举例、探索交流、画图展示、总结反思的过程,实现了高效课堂的构建.
关于“中心对称”的教材解读
(一)不同版本教材的比较分析
人教版教材把“中心对称”放在九年级上册最后一章讲解,因为“中心对称”属于图形的旋转,而相对于图形的平移、图形翻折,图形的旋转比较难,所以放在三角形与四边形都学完后才学习.华师版教材把“中心对称”放在七年级下册最后一章,认为图形的平移、图形的翻折、图形的旋转都是全等变换,应放在一起学习.
(二)教学目标
1.认识并欣赏自然界和现实生活中的中心对称图形.
2.了解中心对称、中心对称图形的概念,通过观察等方法探索中心对称的基本性质:中心对称的图形中,对应点的连线经过对称中心,且被对称中心平分.
3.已知图形与对称中心,能画出它的中心对称图形.
4.通过一系列数学活动,积累探索图形性质的经验,感受图形变换的思想.
(三)教学重点与难点
1.了解中心对称、中心对称图形的概念,通过观察等方法探索中心对称的基本性质.
2.已知图形与对称中心,能画出它的中心对称图形.
“中心对称”点线式教学节选
(一)看中心对称——欣赏生活中的中心对称图形
多媒体展示:工商银行的标志、英国国旗、大风车、太极图、中国结、东风车标.
师:请同学们欣赏每张图片,发现它们的共同特征是什么?

图1
生(猜想):这些图形的共同特征是绕中心旋转180°后都能与自身重合.
师(多媒体演示):让这些图形绕中心旋转180°.
生:旋转后的图形与原图形互相重合.
学习材料源于生活,教学过程实现了由静到动,由动到静,学生用心观察,细心体会,发现了生活中的对称美.
(二)说中心对称——中心对称的概念与特征
师:仿照轴对称图形、轴对称、对称轴的概念,请尝试给中心对称图形、中心对称、对称中心下定义.
生:如果一个图形绕中心旋转180°后能与自身重合,那么这样的图形就叫作中心对称图形.两个图形关于这一点成中心对称,这一点叫作对称中心.
师:举出不是中心对称图形的反例?
生:轴对称图形中,等腰三角形、等腰梯形不是中心对称图形.
师:观察图2,△ABC与△DEF关于点O成中心对称,连接AD,BE,CF,你能发现什么吗?并说说你的理由.
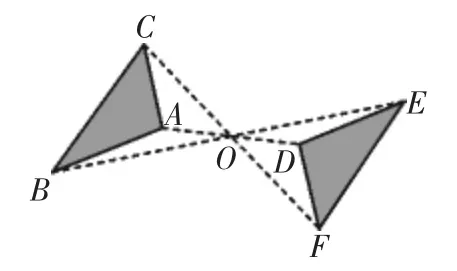
图2
生:对应点的连线AD,BE,CF都经过对称中心O,并且被对称中心平分,即OA=OD,OB=OE,OC=OF,因为其中一条线段绕点O旋转180度后能与另一条线段重合.
生:还可以得到AB=DE,AC=DF,BC=EF.根据边角边公理,得△AOB≌△DOE,△AOC≌△DOF,△BOC≌△EOF,所以AB=DE,AC=DF,BC=EF.
生:还可以得到AB∥DE,AC∥DF,BC∥EF,因为△AOB≌△DOE,△AOC≌△DOF,△BOC≌△EOF,所以∠ABO=∠DEO,∠ACO=∠DFO,∠CBO=∠FEO,所以AB∥DE,AC∥DF,BC∥EF.
师:很好,也就是说,成中心对称的两个图形中,对应线段平行且相等(有时会在同一直线上),对应角相等,两个图形是全等形.
新课标指出,问题情境有利于激发学生的学习兴趣.教学中,笔者立足于学生的最近发展区,选取生活中的图片,让学生感知中心对称图形,概括它们的共同特征,为学生搭建了“脚手架”,能使学生从不同视角思考问题,认识事物的本质.
(三)找中心对称——图形识别
1.如图3所示,哪些图形是中心对称图形?

图3
2.如图4所示,哪些图形成中心对称?
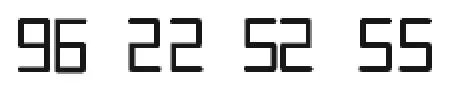
图4
3.如图5所示,由5个全等的小正方形组成的图案,请用两种方法分别在图中添加1个正方形,使整个图案成为中心对称图形?

图5
教学中,笔者让学生辨别中心对称图形、中心对称,加强学生对这两个概念的理解,使学生进一步体验中心对称的美学价值.
(四)画中心对称图形——全等变换
师:(1)已知两个图形成中心对称,如何找到对称中心呢?(2)如何画一个点关于另一个点对称的图形呢?如何画一条线段关于一个点对称的图形呢?如何画一个三角形关于某一个点对称的图形呢?(3)画一个图形的中心对称图形,基本步骤是什么?
生:……
(五)等分中心对称图形——拓展延伸
1.如图6所示,在平行四边形中挖去一个矩形,请用无刻度的直尺作出一条直线,将剩下图形的面积平分.

图6
2.如图7所示,有一块方角形钢板,请用三种不同的方法,用一条直线将其分为面积相等的两部分.
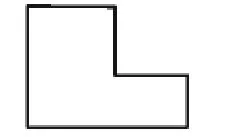
图7
从横向联系看,通过看中心对称、说中心对称、找中心对称、画中心对称、等分中心对称等活动,活动推进顺畅,学生立足于观察与实验、猜测与计算、验证与推理,形成了知识的系列结构.
从纵向联系看,画中心对称图形时,由一个点到一条线段,再到一个三角形;等分中心对称图形时,由外显的两个图形组合,到内隐的两个图形组合,图形逐渐复杂,学生的动手能力逐级攀升,在动手操作中慢慢领悟了数学知识,同时也构建了数学与生活的有机联系.
“点线式”教学法反思
(一)以生为本,创设问题
好的数学课堂对学生的影响深远,教师教学要回归教学本质,即回到学生与教材中,立足于学生的生活与最近发展区设置问题,以问题导引教学的推进.关于问题的设置,既要尊重教材又要敢于突破,做到活用、善用.教学中,笔者以生为本,以教材为依托,从横向、纵向两个角度延展,以看、说、找、画、等分的层次线呈现教学流程,抓住问题的关键与本质.
(二)模型建立,积累经验
教学中,笔者以“问题情境—数学抽象—模型应用”为路径:首先,让学生理解掌握最基本的知识与技能;其次,建立起中心对称与中心对称图形的模型;最后,运用数学模型解决问题,帮助学生积累了数学活动经验,实现了高效课堂的构建.
(三)活动设计,发展思维
教学中,教师应重视数学活动的设计,虽然本课的内容较多,但笔者进行了合理有序的安排.通过观察中心对称图案,画中心对称图形等,学生学会了思考的方法,培养了动手操作能力和思维能力.
(四)建立联系,整体建构
笔者关注知识间的联系和图形之间的相互关系,要求学生类比轴对称图形、轴对称、对称轴得出中心对称图形、中心对称、对称中心等概念,这种由点及线的构成,打通了知识学习的壁垒,实现了知识的整体建构.
