“六环节”高效复习课堂的构建与思考
——以八年级上学期的期中几何复习课为例
2022-12-25廖莉丽
廖莉丽
南京师范大学盐城实验学校 224700
八年级上学期的期中几何复习课时安排一般为三个课时,“六环节”高效复习课堂的构建旨在引导学生查漏补缺,形成知识结构,在探究解题策略与领悟思想方法的同时,提高解决问题的能力.
复习内容与素材
(一)复习内容
本次复习课的内容包括“全等三角形”“轴对称图形”“勾股定理” 三个章节.其中的知识要点有:全等三角形的性质、全等三角形的判定方法、线段垂直平分线的性质、角平分线性质、尺规作图、等腰三角形的性质与判、等边三角形的性质与判定、勾股定理及其逆定理、勾股定的应用.
(二)复习素材
如图1所示,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF,BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,且∠EAC=∠FAB.图中有几对全等的直角三角形?为什么?
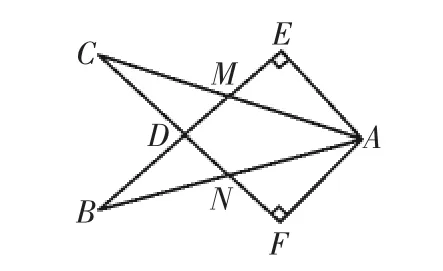
图1
预设答案因为∠EAC=∠FAB,所以∠EAB=∠FAC,因为∠E=∠F=90°,BE=CF,根据角角边定理,得△AEB≌△AFC,所以AE=AF.因为∠EAC=∠FAB,∠E=∠F=90°.根据角边角公理,得△AEM≌△AFN,所以图中有两对全等直角三角形.
问题改编(1)图中有几对全等三角形?为什么?(2)除上述全等三角形的结论外,还有其他结论吗?(3)若连接BC,AD,那么直线AD与直线BC有何位置关系?(4)当∠CAD=30°时,△ABC是什么形状的三角形?为什么?(5)当∠CAD=45°时,线段AG与BC有何数量关系?为什么?(6)已知AC=13,CF=12,∠C=∠NAC,如何求ME的长呢?
教学过程
(一)原发式质疑
师:图1中有几对全等三角形呢?为什么?
生:图1中有4对全等三角形,分别是△AEB≌△AFC(已证),△AEM≌△AFN(已 证),△ABM ≌△ACN,△BDN≌△CDM.因为△AEB≌△AFC(已证),△AEM≌△AFN(已证),所以AC=AB,AM=AN,因为∠MAN公用,根据边角边公理,得△ABM≌△ACN,因为△AEB≌△AFC(已证),△AEM ≌△AFN(已证),所以∠C=∠B,AC=AB,AM=AN,所以MC=BN,因为∠CDM=∠BDN,根据角角边定理,得△BDN≌△CDM.
设计意图笔者把“图1中有几对全等的直角三角形?为什么?”换成“图1中有几对全等的三角形?为什么?”,由此得到了原发性问题,课堂上再由原发性问题出发,通过笔者的启发引导,学生的思考探究与交流,巩固了全等三角形判定方法的知识.
(二)关联性追问
师:观察图1显示的图形,你还能得到什么结论呢?
生:相等的线段包括:AE=AF,AM=AN,AC=AB,MC=BN,BE=FC,EM=FN,DM=DN,BD=CD,BM=CN,DE=DF;相等的角包括:∠EAM=∠FAN,∠EAN=∠FAM,∠E=∠F,∠EMA=∠FNA =∠CMD=∠BND,∠CME=∠BNF=∠DMA=∠DNA,∠CDM=∠BDN,∠CDB=∠MDN,∠C=∠B.因为DE=DF,AE=AF,所以AD是线段EF的垂直平分线,所以AD平分∠EDF,平分∠MAN,平分∠EAF.
笔者重点引导学生关注为什么AD平分∠EDF,为什么到角两边距离相等的点在角平分线上,要限制在角的内部?学生通过小组讨论发现,如图2所示,在角的外部也存在到角两边相等的点,但这个点不在这个角的平分线上.由此,笔者帮学生梳理了角平分线性质定理及逆定理,明确了这两个定理的内涵与外延.

图2
师:如图3 所示,连接BC,观察图形,直线AD与线段BC有何位置关系?试证明你的猜想,并说明证明依据.

图3
生:直线AD垂直平分线段BC,因为AC=AB,所以△ABC是等腰三角形,因为AD平分∠CAB,根据等腰三角形三线合一,得AD垂直平分线段BC.
生:直线AD垂直平分线段BC,也可以这样证明,因为CD=BD,AC=AB,根据线段垂直平分线定理的逆定理,得点A,D在线段BC的垂直平分线上,根据两点确定一条直线,得直线AD是线段BC的垂直平分线.
两名学生从两个不同的角度证明了同一个结论,笔者借此复习了等腰三角形三线合一的性质、等边对等角的性质、线段垂直平分线的性定理及逆定理.
设计意图本环节通过解决两个关联性问题,发展了学生的观察联想能力、合情推理能力.在学生说明证明依据的过程中,复习了基本定理,通过一道试题两种证明方法,开阔了学生的思路.在定理的辨析过程中,学生明晰了定理的外延与内涵,经历了问题的分析与解决的过程,感受到解决问题的基本路径是归本溯源.
(三)拓展式延伸
师:(1)当∠CAD=30°时,△ABC是什么形状的三角形?为什么?(2)当∠CAD=45°时,线段AG与BC有何数量关系?为什么?
生:……
设计意图本环节的两个问题通过强化条件“∠CAD=30°”,得到了△ABC是等边三角形,复习回顾等边三角形的性质与判定;通过强化条件 “∠CAD=45°”,得到了等腰直角三角形,复习回顾直角三角形斜边中线的性质,体现了从一般到特殊的数学思想.
(四)深耕式拓展
师:如图1所示,已知AC=13,CF=12,∠C=∠NAC,如何求ME的长呢?
生:在Rt△ACF中,因为AC=13,CF=12,由勾股定理,得AF==5,因为∠C=∠NAC,由等角对等边,得CN=AN,设NF=x,则CN=AN=12-x,在Rt△ANF中,由勾股定理,得AN2=NF2+AF2,即(12-x)2=x2+25,解得:x=因为△AEM≌△AFN,所以ME=NF=
设计意图本环节一方面复习了勾股定理,另一方面重点关注解题策略与数学思想.在解题思路方面,求线段的长,常用方法就是利用勾股定理.在数学思想方面,渗透了方程思想与转化的思想.
(五)开放式拓展
师:欲有结论AD平分∠CAB,原题中的∠E=∠F=90°还可以换成其他条件吗?
学生在充分考虑与小组讨论的基础上,提出以下结论,如:∠E=∠F,或∠C=∠B,或者AC=AB,或者ME=NF等.
(六)结构式归纳
通过本节课的学习,我们复习了哪些知识?结合你的学习体验,请分享其中的思想方法.
学生归纳后,教师板书,这一环节进一步帮助学生完善知识结构,领悟数学思想方法,提炼解题策略.
阶段性几何复习的思考
(一)如何设计复习的问题
设计的原发性问题要具有基础性、典型性、生成性[1].原发性问题要源于教材,难度小,能在5分钟之内完成.设计的问题要能覆盖复习章节的相关知识,把学生的疑点、易错点都暴露出来.所谓生成性是指以原发性问题为基础,拓展延伸出新的问题.新问题可以是质疑原问题、追问原问题,也可以是变式、延伸与拓展类问题.本节课以一道典型题为题根,复习了全等三角形的判定方法,梳理了角平分线性质定理、线段垂直平分线性质定理、特殊三角形的性质等基础知识,一连串的问题,关联了教材内容,联系了思想方法,把原发性问题添加条件生成新问题,体现了问题设计的基础性、典型性与生成性.
(二)如何选择复习路径
几何的阶段性复习可分为六个环节,分别是原发式质疑、关联性追问、拓展式延伸、深耕式拓展、开放式拓展、结构式归纳[2].环节一是复习的源头,通过原发式问题的解决,学生弄清了问题的解决方法、解决问题的依据以及用到的知识.环节二侧重于知识的重构,进一步明确知识间的联系,引导学生提出自己的疑问,解决关联性问题.环节三与环节四通过强化题根或弱化题根,解决深层性问题,让学生在一题多解与一题多变中体验证法的多样性.环节五以强化学习为重点,突破难点,提升学生的思维品质.环节六是复习课的点睛之笔,学生回顾本节的知识、方法与策略,将这三个方面的收获结构化,从而培养自身的归纳概括能力.
(三)如何让复习课堂有生成
要想让复习课堂有生成需要从四个变化着手:一是问题的设置从追问到质疑,从教师提出问题到学生质疑,引发学生讨论,解决学生的疑惑;二是思维从封闭到开放,所谓开放包含三个方面:条件开放、结论开放和方法开放;三是方式从单向到双向;四是学习路径从固化到灵活.
