我国数学教育博士学位论文研究方法的使用现状与反思
——基于2002—2021年博士学位论文的考察
2022-12-24周菊玲李湘艺
周菊玲,李湘艺,刘 芹
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
教育研究中的定量研究方法,自引入中国教育科学领域,虽逐渐被重视,但比起已经将定量研究作为教育研究和期刊论文的基本范式,在进行项目研究、学术交流时普遍应用的国家[1],在我国,定量研究方法还没有得到足够重视,未被广泛使用。数学教育博士学位论文是我国数学教育领域的优秀研究成果,其学术代表性能够引领我国数学教育的研究方向,研究方法的科学性代表了我国数学教育研究的水平,从中可以分析我国数学教育研究中定量研究方法的使用情况。近年来,一些学者对我国数学教育博士学位论文进行了分析,徐文彬、喻平就2002—2005年期间的23篇数学教育博士学位论文的选题与韩国数学教育博士学位论文进行了比较研究[2];李涵、傅海伦对64篇2002—2009年数学教育博士学位论文的数量情况、院校分布、选题、主题等进行了统计分析[3];李卓、于波、张勇对1993—2016年255篇数学教育博士学位论文从院校分布、研究主题、研究方法等三个维度进行了统计分析,并在数学教育研究主题和研究方法等方面提出了建议[4];康玥瑗对34篇2002—2006年公开发表的数学教育博士学位论文,从论文数量、研究主题进行了统计分析,对采取的研究方法进行分析,发现其中使用的研究方法比较单一,水平不高,并提出应将现代数学中一些适合教育研究的方法引进来的建议[5];吕世虎、刘瑞娟除了对92篇2002—2011年公开发表的数学教育博士学位论文的数量分布等情况进行了统计分析以外,也对其中的研究方法进行了统计分析,发现在这些博士论文中所使用研究方法的平均种类呈逐年递增的趋势[6]。以上这些对中国数学教育博士学位论文中所使用研究方法的分析,只是做了简单的统计描述和概括分析,对数学教育博士学位论文中定量研究方法使用情况的详细分析以及对定量研究方法的误用及纠正建议进行的研究还鲜有见到。因此,文章以234篇2002—2021年公开发表的中国数学教育博士学位论文为研究对象,详细梳理其中所使用的研究方法,统计分析各种定量研究方法,整理出定量研究方法的误用情况,并尝试给出相应的纠正建议,总结定量研究方法在我国数学教育研究学界的应用现状。
1 研究对象与方法
1.1 研究对象
首先在中国知识资源总库(CNKI)中,以“数学教育”为主题进行检索,选取2002—2021年公开发表的我国数学教育博士学位论文(以下简称学位论文)234篇,并下载。接着,粗略查看以上全部学位论文的题目、关键词、摘要、目录、正文等,保留其中使用了定量研究方法的文章,共141篇(包括仅仅使用描述性统计分析的学位论文)。最后,再一次浏览141篇学位论文的全文,记录各种定量研究方法、使用频次和软件工具的使用情况等。
1.2 研究工具
采用Excel人工记录学位论文中各种定量研究方法的使用情况,包括样本抽取的方式、样本容量及推断情况以及软件工具的使用情况,并进行了相应的统计分析。
2 我国数学教育博士学位论文使用定量研究方法的现状分析
2.1 总体情况
从图1趋势线可以看出,2002—2021年学位论文总体数量呈上升趋势,说明我国数学教育博士的培养总体上呈现了良好发展和稳步上升的态势,期间也有个别年份学位论文数量有向下的波动,波动周期大约为3~4年,这刚好与数学教育博士培养周期吻合。
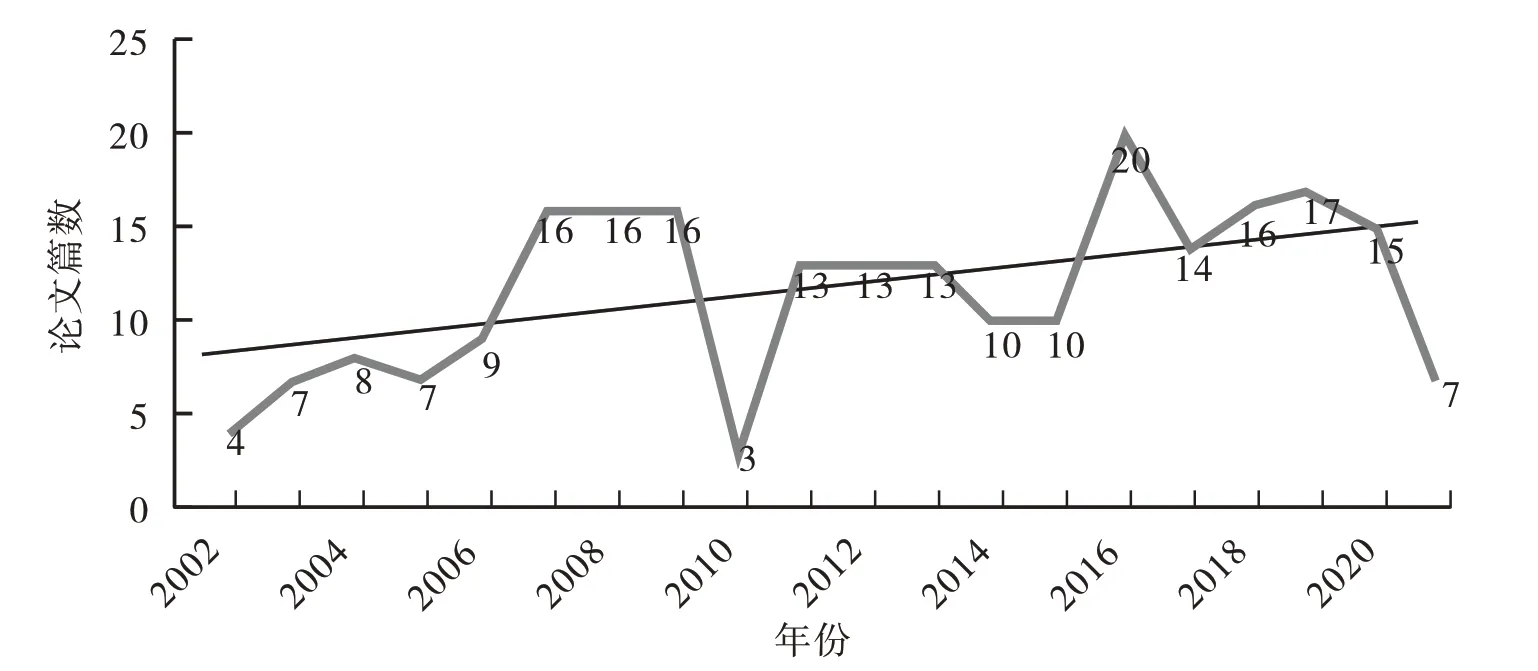
图1 2002—2021年数学教育博士学位论文总体数量统计
2002—2021年期间,自2002年起前5年每年论文产出数量较少,以后每年论文产出数量都在10篇以上(除了2010年和2021年以外),2016年达到了峰值20篇。2021年的论文数量出现了较大回落,大概与2020年突发的新冠肺炎疫情使研究有所延缓或停滞。学位授予单位也从2002年的南京师范大学、中国社会科学院研究生院、西南师范大学(作为最早2002年有论文产出的学校,2005年经合并后称西南大学)3家发展到目前的24家(表1)。
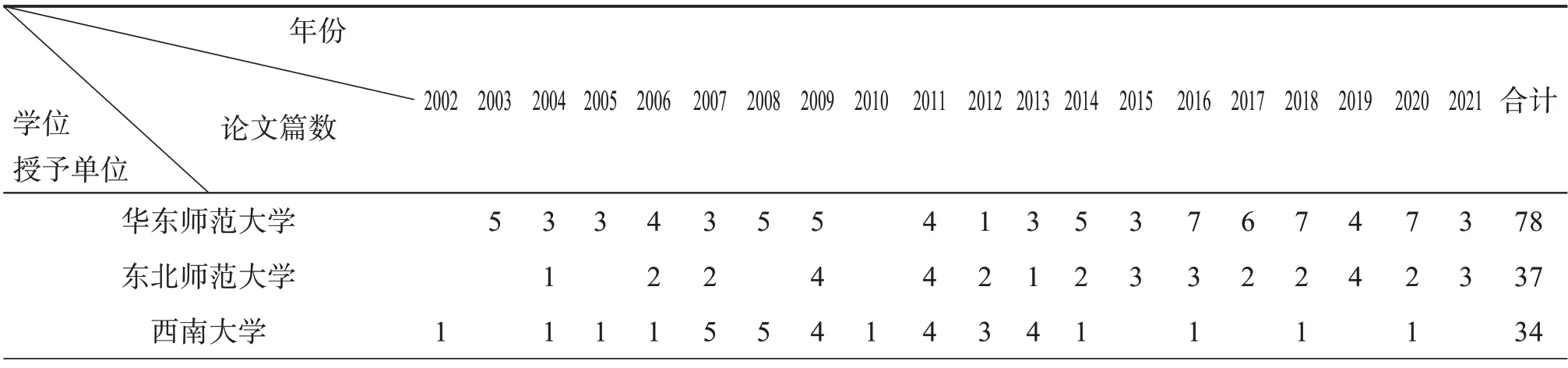
表1 2002—2021年学位授予单位及学位论文数量统计

年份学位授予单位论文篇数2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 2021合计南京师范大学内蒙古师范大学华中师范大学西北大学陕西师范大学广州大学西北师范大学哈尔滨师范大学吉林大学华中科技大学曲阜师范大学厦门大学山东师范大学山西大学上海师范大学天津师范大学贵州师范大学福建师范大学浙江师范大学中国科技大学中国社会科学院研究生院合计2 1 3 1 2 4 1 1 2 1 1 1 1 2 1 2 26 12 1 3 2 2 2 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 2 1 1 1 1 2 2 1 2 2 1 1 2 1 1 1 1 1 1 1 1 4 8 6 6 5 3 3 3 2 1 1 1 1 1 1 1 1 1 1 1 7 8 7 9 161616 3 1313131010201416 1 1 1 1715 7
其中,华东师范大学产出论文数量最多,共78篇,占论文总数的33.33%;其次是东北师范大学,共37篇,占15.81%;紧随其后的是西南师范大学论文数量为34篇,占14.53%;前四家单位合计产出的论文数量占总数量的74.79%,为我国数学教育领域培养了大量的人才。
2.2 使用定量研究方法的学位论文数量分布情况
从图2的曲线走势可以看出,使用定量研究方法的论文数量总体呈现上升趋势。从柱状图可以看出,使用定量研究方法的论文数量呈现波浪形走势,前6年使用定量研究方法的论文数量增幅较大,但从2007年到2015年使用定量研究方法的论文数量又呈现较大回落,2015年以后定量研究方法数量虽有增长,但增加的幅度并不大,且于2019年又出现回落。一方面说明在我国数学教育研究学界,定量研究方法还没有得到足够的重视,另一方面可能是学位论文作者大多没有系统地学习过定量研究方法,对数学教育研究中使用定量研究方法的认识还不到位。2015年“全国首届教育实证研究论坛”的召开对数学教育研究学界定量研究方法的使用也没有起到很好的推动作用,这应该引起各博士培养单位的重视。“工欲善其事,必先利其器”,要提高教育科研水平,就必须掌握合适的研究方法[1],定量研究方法、手段和技术是促进教育科学取得突破性进展的关键[7]。
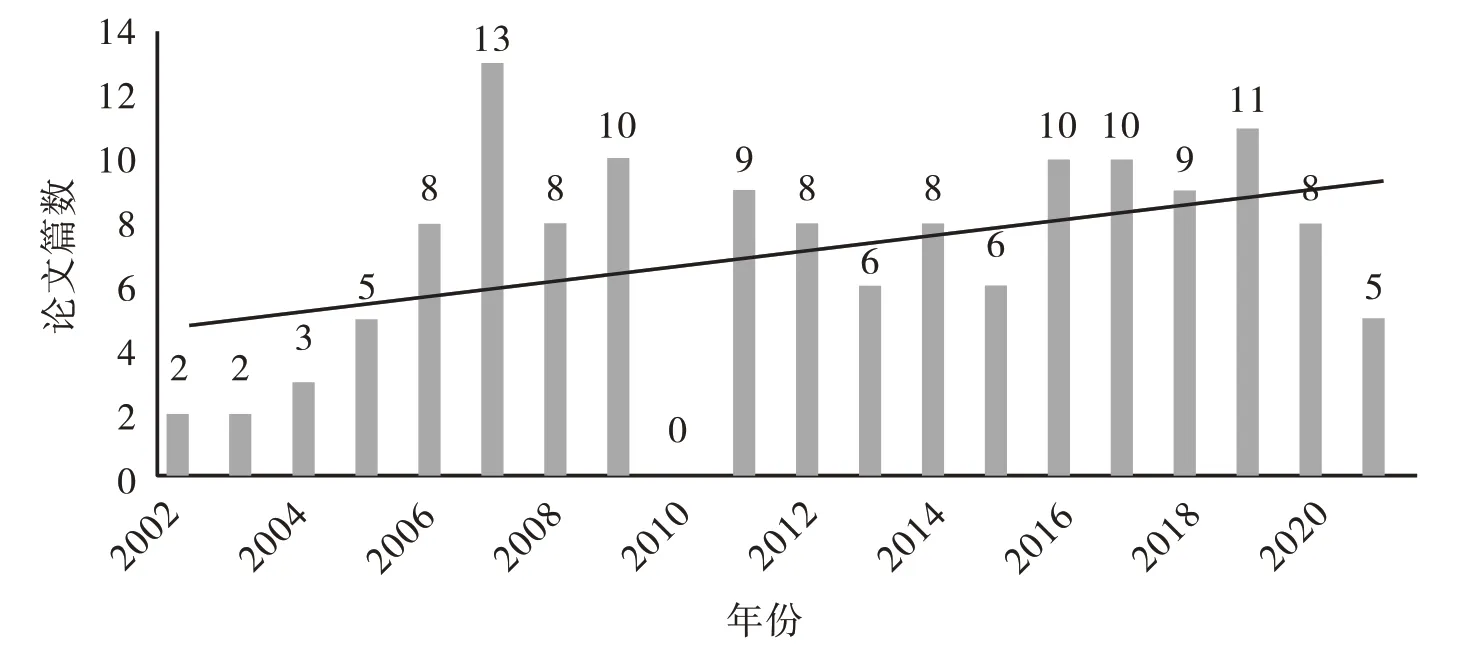
图2 2002—2021年使用定量研究方法的论文数量统计
2.3 各种定量研究方法及软件工具的使用情况
从表2中可以看出,定量研究方法的使用较为广泛,除了描述性统计,方差分析(25.21%)、T检验(21.8%)、相关分析(11.97%)、回归分析(8.12%)等这些传统的数据分析方法以外,还有个别论文中应用了结构方程模型(SEM)、因子分析(FA)、层次分析法、模糊综合评判等定量研究方法。此外,一些在国际上已经推广的适合教育领域研究使用的行动研究方法,还没有得到应用。使用最多的分析软件是SPSS软件,其次是Excel和AMOS软件。
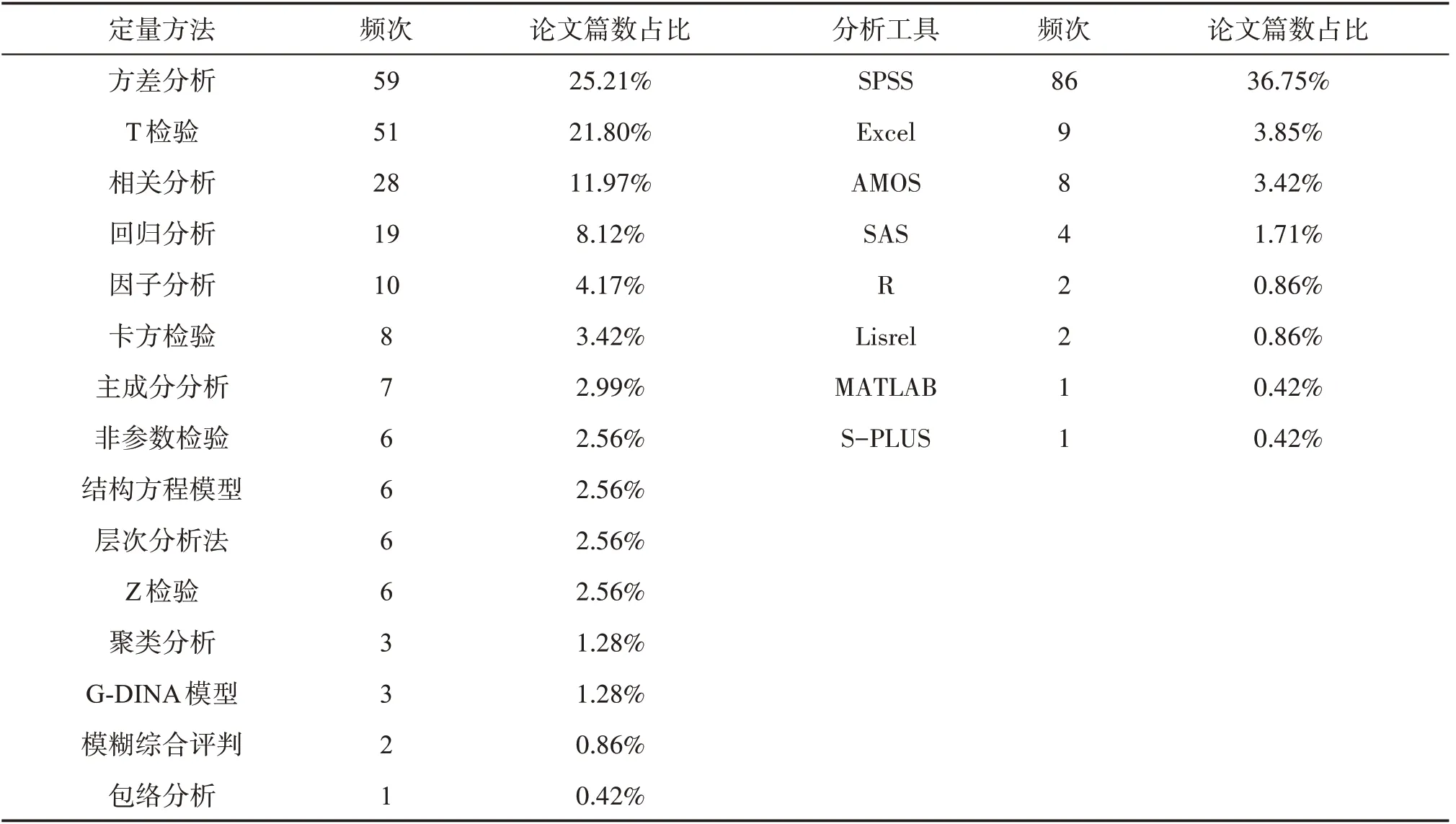
表2 定量研究方法和软件工具的使用频次和占比统计
3 存在的问题及纠正的建议
正确使用定量研究方法对数学教育研究的重要性不言而喻。在分析中发现,使用定量研究方法时存在一些问题,例如,对定量研究存在误解、忽略定量研究方法的适用条件、不恰当地使用统计分析方法等使研究结果的正确性大打折扣。为此,文章将梳理以上学位论文中出现频率较高的方法误用情况,并给出纠正建议。
3.1 定量研究与实证研究
对定量研究存在误解。实证研究的思维方法和基本特征之一是量化方法,但不能将实证研究与定量研究混为一谈。定量研究是指确定事物某方面量的规定性的科学研究,就是将问题与现象用数量来表示,进而去分析、考验、解释,从而获得意义的研究方法和过程。实证研究即用实证证据进行研究。不论是以确定数量的程度为目的,还是以量化的程度支持对性质的判断,只要是基于事实和证据的研究,就是实证研究,而不在于其是定量分析还是定性分析。实证研究方法有狭义和广义之分,狭义的实证研究方法是指利用数量分析技术,分析和确定有关因素间相互作用方式和数量关系的研究方法。广义实证研究方法泛指所有经验型研究方法,如:调查研究法、实地研究法、统计分析法等。建议使用定量研究方法时,应将其区别于实证研究。
3.2 样本容量、取样方式和统计推断
绝大多数统计推断方法建立在简单随机样本的前提条件下,但是很多学位论文没有考量统计推断适用的条件,样本的抽取或采取方便取样,或对样本的选取方式不加任何说明和解释,直接将采集到的数据进行估计、检验等统计推断;对样本的抽取没有进行设计和选择;对样本容量不加考虑、对缺失数据没有进行预处理;将描述统计分析的研究结果做任意的推广。鉴于以上这些不规范使用定量方法的情况,给出如下建议:
关于样本的容量:一方面,根据统计推断理论,一般情况下样本容量足够大时统计推断的误差会减小,精度会提高。另一方面,样本容量足够大(n>30),也可以一定程度上保证分布的正态性。
关于取样方式:简单随机取样在理论上是严格的,对于取样总体也更具代表性,并且也可以将研究结果推广到样本所属的总体中去。但是实际应用中无法完全按照理论进行操作,在实际的教育研究中,可以将各种简单的取样程序混合使用,例如,在取样的第一阶段采用聚类取样,再进行分层取样,最后进行简单随机取样。采用复杂取样的实质就是通过各种不同的方法,得到富有变化的概率样本,尽可能在效率和效益上满足取样需求[8]。
关于统计推断:要根据样本的情况决定采用的方法和做推广,如果样本是非概率抽样,无法知道对取样总体的代表性程度,即不能保证真正代表取样总体,故不能将建立在概率抽样基础上的统计推断理论用于此,而将研究结果推广到样本所属的总体中去[8]。所以研究者应选择方法上精确、理论上严密的概率取样或随机取样的方法。
3.3 关于T检验的正态性
在研究均值的差异性时,常常使用独立样本T检验或配对样本T检验,而T检验只适用于数据资料服从正态分布或近似服从正态分布的情形。虽然大多数学位论文能够根据样本具体情况,选择使用独立样本T检验或配对样本T检验,但在进行检验时忽略了对样本数据正态性的要求。
建议:在使用T检验进行分析前,需先检查数据是否服从正态分布或近似服从正态分布,当样本容量较小时,可以通过图示法(Q-Q图、P-P图)、移动差法、W检验、D检验、Kolmogorov D检验和卡方检验[9],进行正态性检验;如果结果符合正态分布则使用参数检验的方法[10],如果不服从正态分布或近似服从正态分布时,或者使用非参数检验中的独立样本检验—曼.惠特尼U检验等[11],或者先对数据进行对数变换等,变为正态或近似正态后,再进行T检验。否则可能使分析结果出现偏差进而影响推断结果的可靠性。
3.4 关于方差分析
两组以上样本的差异性检验需使用方差分析,方差分析之前没有进行方差齐性检验。如果数据不满足正态性,则进行方差分析就不合适。所以,当数据资料为偏态分布时,应先进行对数变换、平方根变换、倒数变换、平方根反正弦变换等,变为正态或接近正态性后,再进行方差分析;用Bartlett法检验等方差性,如果相应的卡方检验量判断方差齐性不满足,则不适合进行方差分析。
4 反思
4.1 重视定量研究方法的使用
数学教育博士是数学教育研究领域先进思想和科学方法的引领者,其研究成果的学术性、前沿性树立了其在该领域的威望,所使用的研究方法一定程度上代表了该领域的研究水平、引领着研究趋势。随着我国数学教育研究的深入发展,以及“教育实证研究论坛”的召开,定量方法被越来越多地应用在数学教育研究中,正如文献中所强调的:定量研究方法、手段和技术是促进教育科学取得突破性进展的关键[1,7]。但是目前,在新方法和新技术的引进和使用上还处于落后地位。从前文的统计中可以看到,定量研究方法虽然在不少学位论文中被使用,但频率还不够高,使用还不够得心应手。因此提出以下建议。
一方面,定量研究方法是薄弱项,各培养单位应重视定量研究方法,加强对定量研究方法使用的引导,例如,可以在博士研究生培养中开设相关课程;多关注国际数学教育研究中的新方法和新技术,如元分析结构方程模型、多层结构方程模型(MSEM)、大数据挖掘技术等[1],以尽快提高研究生应用定量研究方法的水平。
另一方面,各培养单位也可以通过举办定量研究方法的研讨会或学术交流会等形式,由相关专家介绍经验,这样既可以促进研究者自身通过应用定量研究方法进行训练,又能提高定量研究方法普及度,进而推动其发展。
除此之外,还可以举办一些中国数学史教育的讲座,用数学家研究数学、运用数学的励志故事,激发学生的爱国情感,培养学生热爱科学、崇尚科学的精神,进而激励青年学子为振兴中国科技而努力奋斗[12]。
4.2 规范定量研究方法的使用
在浏览学位论文时,还发现其中普遍存在统计方法的简单模仿,甚至误用和错用,鉴于这些具体问题,提出以下建议:
首先,要明确数据资料的收集,并对抽样的程序、取样的方法进行说明,以保证研究的有效性。
其次,要重视方法的条件。几乎所有的定量研究方法都有其适用的条件,不同方法的适用条件也有差别。故对资料进行定量分析之前,必须充分分析资料的类型、分布特征等因素;使用某种定量方法时,须先考虑其适用条件,如果进行概率抽样,而样本容量偏小且非正态,就应慎重选择统计推断方法;如果样本容量较大时,使用差异性检验、回归分析、方差分析等方法时,应先进行正态性检验、方差齐性检验和独立性检验,避免因误用方法而得出错误的结论,以提升结果的可信度。
4.3 加强定量研究方法使用的管理
提高数学教育研究者运用定量研究方法的学术素养,这种素养的训练和养成一方面依赖于教育学术(者)共同体的制度性规范,另一方面也有赖于学术研究者的自觉意识[13-14]。所以,一方面,研究生应加强自身学术能力,规范写作,提高使用定量分析方法的素养和水平;另一方面,培养单位不仅要加大研究生使用定量研究方法的训练,关键要加强学位论文的评审环节,争取使研究生在定量研究方法的使用上不出漏洞、减少偏差。
综上,这二十年来中国数学教育博士论文的产出数量总体呈增长的情况下,培养单位以我国东南部的高校居多,西北地区除了陕西西安有两所高校,甘肃兰州一所高校外,整体很少。这种产出分布不均衡的状态,随着国家对西北地区特别是新疆加大教育投入和对口支援帮扶,在未来的几年中将会有所好转。新疆的高校也应该从自身做起,增强发展的主动性和创新性[15],主动作为,不仅要重视与基础教育课程改革密切相关的数学课程研究、数学教学研究、数学学习研究、数学教师专业发展等各方面的研究,同时应该发挥在数学教育上的后发优势,在研究方法上重视学习国际数学教育研究领域先进的定量研究方法,不断更新定量研究的方法,使我国数学教育研究走上规范、科学、多元、平衡发展之路,促进我国数学教育研究的整体发展。
