基于手写识别的K-means聚类分析

蔡鲲鹏

（阜阳师范大学 计算机与信息工程学院，安徽阜阳 236041）

社会分工的计算机化和功能强大的数据收集、存储能力让可用数据得到了爆炸性的增长。用户可以通过用户界面对于事务进行查询、处理，并能方便、灵活地访问数据。但是串行处理件对于大型数据集往往有心无力，因为这些工具建立在某些操作平台或是在虚拟机上，本身有其内存限制，有可能会造成内存溢出现象。在当今许多社会领域中，都需要用到手写数字识别等相关知识。因此，基于加州大学的开放数据集，利用聚类算法对手写数字进行聚类研究，并在此基础上区分出每个人的手写数字笔迹。以往相关研究主要集中在神经网络领域中，例如，沈荣和黄晨介绍了基于深度学习的目标检测算法，提出了一种利用深度学习技术进行手写识别的设计方案［1］。闫伟提出了一种基于深度学习的笔迹识别方法。Beta Elliptic模型首次应用于汉字笔迹识别，对汉字笔画进行切割和分类［2］。但是，近年来也出现了一些其他应用与手写数字识别的算法，例如，陈健、周平等人提出了一种基于胶囊网络的汉字笔迹识别算法，并构建了跟踪采集数据集来模拟在复杂背景下生成的汉字［3］。李大娟、李楠、李琰延等人提出了一种基于Mat PCA和PNN融合的笔迹识别方法［4］。在此基础上，也出现了一些通过聚类算法应用于识别方法的应用研究，例如，张飞提出了一种通过图像的特征提取、模式相似性测量的一种基于试探的聚类识别算法［5］。沈秀娟、薛烁等人提出了一种加权K-means聚类算法［6］。郭西风提出了一种基于深度网络的图像聚类算法［7］。以上算法都很好地应用于图像或文本识别，本研究则尝试通过K-means算法进行手写数字的识别，并将聚类结果与现实情况进行验证，如果成功率能达到理想阈值，那就表明聚类算法也可以对手写数字进行识别。

1 算法描述

1.1 算法概述

聚类算法是一种无监督数据挖掘方法，它基于观测之间的距离度量将观测值分组。一个好的聚类方法会产生高质量的聚类效果，使同一类别的观测值比较相似，而使不同类别的观测值差异比较大［8］。聚类分析应用广泛，例如，用它可以对客户进行细分，并且也可以针对一些特殊数据集进行处理，使得相似的数据值归为一类。K-means算法的显著优点是原理简单，容易实现，收敛速度快，因此K-means算法更适合用于处理大数据。

1.2 算法原理

在介绍K-means算法之前，需要先阐述密度估计的概念。密度估计是依据众多的可以观察并能测定到的数据集去评估不能观察并测定到的数据集的概率密度函数［9］。在拥有相同密度聚类的前提下，不能够观察并测定出的概率密度函数是等待去研究的一切可能数据整体的确切分布。可以观察并能测定到的数据集可以被看作是取自于该整体的一个随机样本。基于此，提出了一种对于半径值不敏感的K-means算法。

该算法使用一个噪声阈值ξ，具体应用中，可能需要设定不同的阈值来满足不同的密度分布。每个点上的概率密度都有赖于从该点到观测对象的间隔。

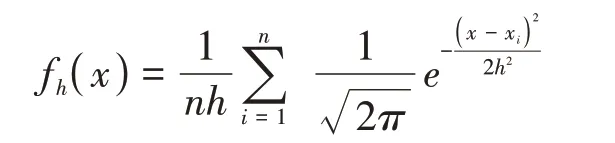
其中，h是用作光滑参数的带宽，K-means运用高斯核估计函数给定待聚类的对象密集度。

将待分析的数据点逐渐关联到每一个x*，并分发到各自的簇中。

K-means的一个个簇就是一个个密度吸引点的小簇X和一个个输入对象的小簇C的集合，使得C中的每个对象都被分发到X中的一个密度吸引点，且每对密度吸引点之间都存在着一条密度大于ξ的路径，通过使用相连的多个密度吸引子，该算法可以发现任何形状的聚类。在聚类前，通常需要对各连续变量进行标准化，使得每个连续变量的均值为0、标准差为1.这是因为方差大的变量比方差小的变量对距离的影响更大，从而对聚类结果的影响更大［10］。在聚类算法中，常用的距离度量有欧氏距离、切比雪夫距离、曼哈顿距离和闵可夫斯基距离等等，本实验的K-means算法采用欧氏距离，公式如下：

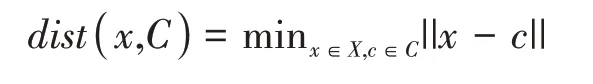
令N表示观测数，Xi表示第i个观测。令K表示类簇数目Ci(i=1,2,…,K)表示属于第i个类簇的观测序号的集合，C(i)(i=1,2,…,N)表示观测i所属类簇的序号。可以看出，C(i)(i=1,2,…,N)和Ci(i=1,2,…,K)代表了描述观测所属类簇的两种不同方式。令vi,…,vk表示各个类簇的中心。K-means的具体步骤如下。

步骤1随机初始化各个类簇的中心（或者随机初始化各个观测所属的类簇）。

步骤2在每次循环中，重复执行（1）和（2）.

（1）将每个观测中心分配到类簇中心与它距离最小的类：

其中，arg min表示寻找参数i的值，使得函数d(xi,vi)达到最小。

（2）令每个类簇的中心为与该类簇内所有观测距离之和最小的向量：

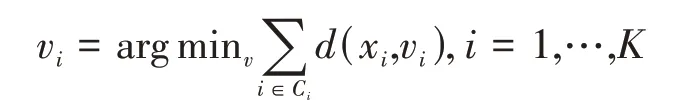
持续循环直到观测聚类不变或者到达收敛条件，收敛条件如下：

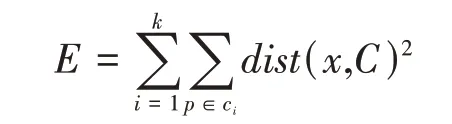
其中，p是给定的数据对象，ci是Ci的形心。在应用K-Means算法时有必要事先制定k个簇数。针对如何制定k值，一般常规的思绪是运用分析的技术，通过比较不同k值得到的结果来确定k值的大概范围，再进行反复迭代，进一步确定k值［11］。基于此，K-Means算法不太适合非凸外形的簇，或者是形状差异很大的簇。

1.3 聚类评估分析

聚类是通过观察学习，并且没有事先给定类标号信息，所以其是无监督学习。处理不同层次类别的能力，其需要能处理诸如图、序列、图像和文档等复杂类型的聚类技术。

聚类分析的方法有以下几种：根据簇之间不同层次结构所进行的划分准则、互斥的簇之间所形成的簇的分离性、通过对象之间的距离来确定两个对象之间的相似性、在整个数据空间进行簇搜索（依据不同的属性）等，其中最常用的是相似性距离度量。

不论是运用何种聚类办法，最重要的问题是如何衡量两个簇之间的有效距离，其中每一个簇即为一个对象集。最为普遍使用的簇之间距离衡量办法有四种，其中|p-p′|是两个对象或是点p到点p′之间的距离，簇ci的均值是mi，ni是簇ci中对象的数目。四种距离如下：

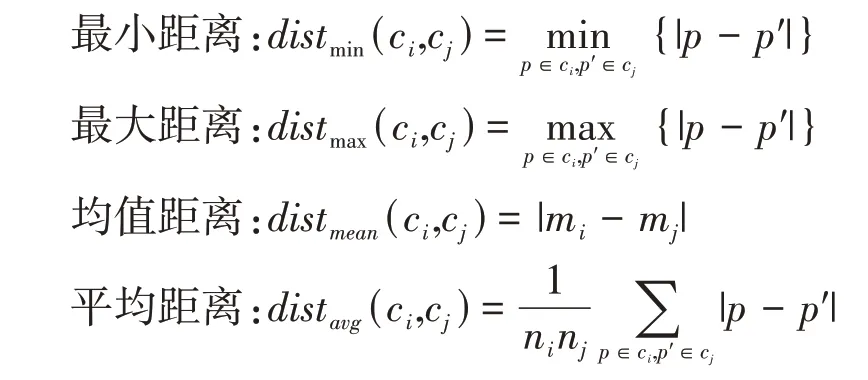
如果把图的结点看作是数据点，图的边构成簇内结点之间的路径，即两个簇ci和cj的合并就对应在ci和cj的最近的一对结点之间添加一条边。最远邻聚类算法采用最大距离distmax(ci,cj)来度量簇之间的距离，当最近的两个簇之间的最小距离超过事先规定的小阈值时聚类过程便会开始，此为另一种连接方式［12］。在簇中，把每个数据点看作是结点，并将其用边线连接，规定两个簇之间的距离是由两个簇之间距离最远的结点间的距离来确定［13］。对于紧凑而且大小近似于相等的簇，最近邻算法会产生比较高质量的簇，如若簇内数据较为稀疏，则重新聚类的簇则毫无意义。

当簇内离群点或是噪声点较多时，使用均值距离或是平均距离来计算簇内对象之间的距离，作为一种折中方法，可以很好地克服离群点过分敏感问题。

聚类评估主要包括估计聚类趋势、确定数据集的簇数、测定聚类质量等。

已知数据集D，将其看成随机变量o的样本，此时需要确定o不同于空间中的平均散布［14］。

（1）在D中均匀抽取n个点p1，p2，…，pn.D中每个数据点都以一样的概率包罗在这个数据集中，对于每个点pi，找到pi在D中的最近邻，设xi为pi与其自身在D中的最近邻的距离，即

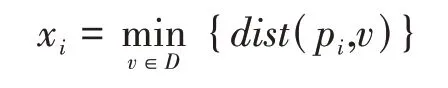
（2）从D中均匀抽取n个点q1,q2,…,qn：

（3）计算霍普金斯统计量H

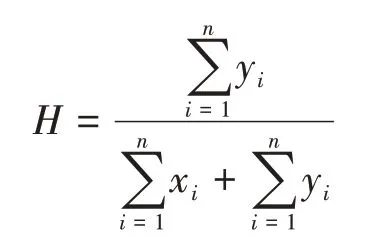
一般而言，对于评价Q是否有效，需要满足4项基本准则：簇的同质性、簇的完全性、碎布袋（rag bag）、小簇保持性（Small Cluster Preservation）。

2 实验目标

总体目标是识别阿拉伯数字的类别，并进一步扩展通过阿拉伯数字提取一些特征点，从而可以使用K-means算法对手写数字进行聚类。

（1）通过数据预处理得到一些干净的数据；

（2）将不同笔迹中的数字准确分组，使其尽可能接近正确值；

（3）采用两种权威的聚类评价标准，可以在处理结果上突出K-means算法的优势，取得比较满意的结果。

3 实验方法

首先，从加州大学的开放数据集中获取数据，然后通过读取数据集的属性来学习数据集的一些特征和维度［15］。其次，引入pandas包对数据集进行清理和预处理。一些空值和索引将被清理掉，清理后的数据保存为本地CSV文件。数据处理完成后，引入K-means算法，并将数据集分为两部分，一是用于训练，二是用于测试，将测试结果绘制成图，引入两个权威指标分别评价聚类结果并绘制图形［16］。结果表明，聚类算法可以有效地对手写数字进行分类。

4 实验评判标准

研究采用两个聚类指标对实验结果进行聚类评价，这两个聚类指标分别是ARI和轮廓系数。

兰德系数（RI）被定义为：

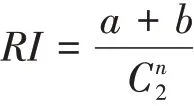
其中，a表示在实际类别信息与聚类结果中都是同类别的元素对数；b表示在实际类别信息与聚类结果中都是不同类别的元素对数。分母表示数据集中可以组成的总元素对数。兰德系数的值在［0，1］区间，当聚类结果完美匹配时，兰德系数为1。对于随机结果，RI并不能保证分数接近于零。为了实现在聚类结果中随机产生的情况下指标应该接近于零，提出了调整兰德系数（ARI），它具有更高的区分度。ARI被定义为：

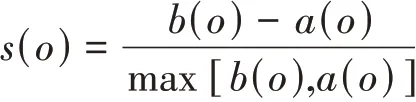
ARI取值范围在［-1，1］，负数代表结果不好，值越大意味着聚类结果与真实情况越吻合。此外，ARI还可以用于聚类算法之间的比较。

轮廓系数是一种内在评估方法，对于n个对象的数据集D，假设D被划分成k个簇，对于每个对象o∈D，计算o到所有它所属簇中其他点的距离a(o)和o到与它相邻最近的一簇内的所有点的平均距离b(o)，则o的轮廓系数定义为：

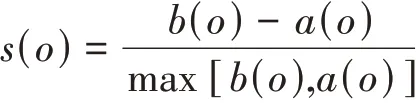
轮廓系数的值为［-1，1］。a(o)反应对象o所属的簇的紧凑型，值越小，簇越紧凑；b(o)反映对象o与其他簇的分离程度，值越大，说明o与其他簇越分离。当o的轮廓系数接近1时，包含o的簇是紧凑的，并且o远离其他簇。当轮廓系数为负值时，说明o距离其他簇的对象比距离与自己同在簇的对象更近。在很多情况下，这是需要避免的。为了度量聚类中簇的拟合性，可以计算簇中所有对象的轮廓系数的平均值。为了度量聚类的质量，可以使用数据集中所有对象的轮廓系数的平均值。通过启发式的导出数据集的簇数取代簇内方差之和，轮廓系数和其他内在的度量也可以用在肘方法中。

5 实验数据集

数据集来源于加州大学机器学习公开数据集，标题为“Optical Recognition of Handwritten Digits”，数据集的官方描述为：使用NIST提供的预处理程序进行提取，来自预打印表单的规范化手写数字位图。参与人员有43人，其中30人贡献了训练集，另外13人贡献了测试集。其中32×32位图被划分为不重叠的每一个小块，在每个小块中统计4×4的块和像素的数量。这将生成一个8x8的输入矩阵，其中每个元素都是一个整数，取值范围0~16。这有利于减小维度，并给出对小变形的不变性。由以上描述可知，完整的手写体数字图像分为两个数据的集合。其中训练数据样本为3823条，测试数据样本为1797条；1个目标维度用来标记每个图像样本代表的数字类别。该数据没有缺失的特征值，并且不论是训练还是测试样本，在数字类别方面都采样得非常平均。

6 实验与结果分析

实验系统为Win10，Python环境，使用Juypter软件。该数据中有3823个训练数据样本和1797个测试数据，并且该数据中没有缺失特征值。文章使用数据集的方式是将一半的训练用于实际训练，四分之一用于验证，四分之一用于依赖作者的测试。

首先，需要检查数据是否为空，如果是，则移除空，所以使用方法notnull（）：

图1 非空判断

其次，需要检查数据中是否存在重复项。如果有重复，则需要删除。使用drop（）后，需要使用reset_index（）将索引恢复为默认整数索引，并删除包含该索引的列。

图2 删除冗余数据

最后，分别保存清洗后的训练集和测试集。下一步，使用聚类评判标准对聚类结果进行评价。首先，需要导入相关的包并读取训练集和测试集。并且分开维度，将训练集和测试集分为64维和1维，因为下面的聚类评价标准需要分别使用1维和多维数据。在这里，可以将k作为一个随机对象并取值为14，然后可以观察ARI和轮廓系数的变化。ARI是调整后的兰德系数，具有很高的区分度，较大的值表示聚类效果更符合实际情况。轮廓系数也可以用来评估聚类质量，较高的轮廓系数意味着更紧凑的聚类和更好的聚类效果。通过不断的实验得出，当k=11时，ARI值和轮廓系数值都比较大。初步得出k=11时聚类效果最好。接下来，需要实验来验证这个结论。

研究需要构建k值模型并从测试集中生成预测值。首先，将k值设置为14，看看聚类效果。得出ARI指标为：

图3 ARI指标

得出轮廓系数为：

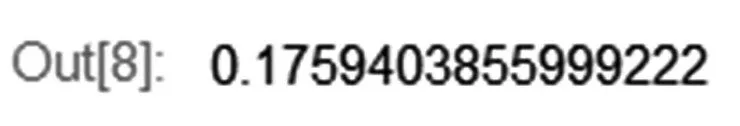
图4 轮廓系数

由以上评判标准可知，ARI的取值范围是-1到1，负数代表不好的结果。值越大，聚类结果与真实结果越一致。同理，轮廓系数的取值是-1到1。值越小，簇越紧凑。值越大，簇越稀疏。从图中的数据可以看出，当k值等于13时，聚类效果一般，说明最好的聚类效果的k值应该小于13，k值可能会出现拐点等于某个值。因此，接下来，研究需要获取一系列的ARI值和轮廓系数值。

ARI的一系列值（k值从1到13）：

图5 ARI的一系列值

轮廓系数一系列值（k值从1到13）：

图6 轮廓系数的一系列值

接下来，分别绘制ARI和轮廓系数曲线：

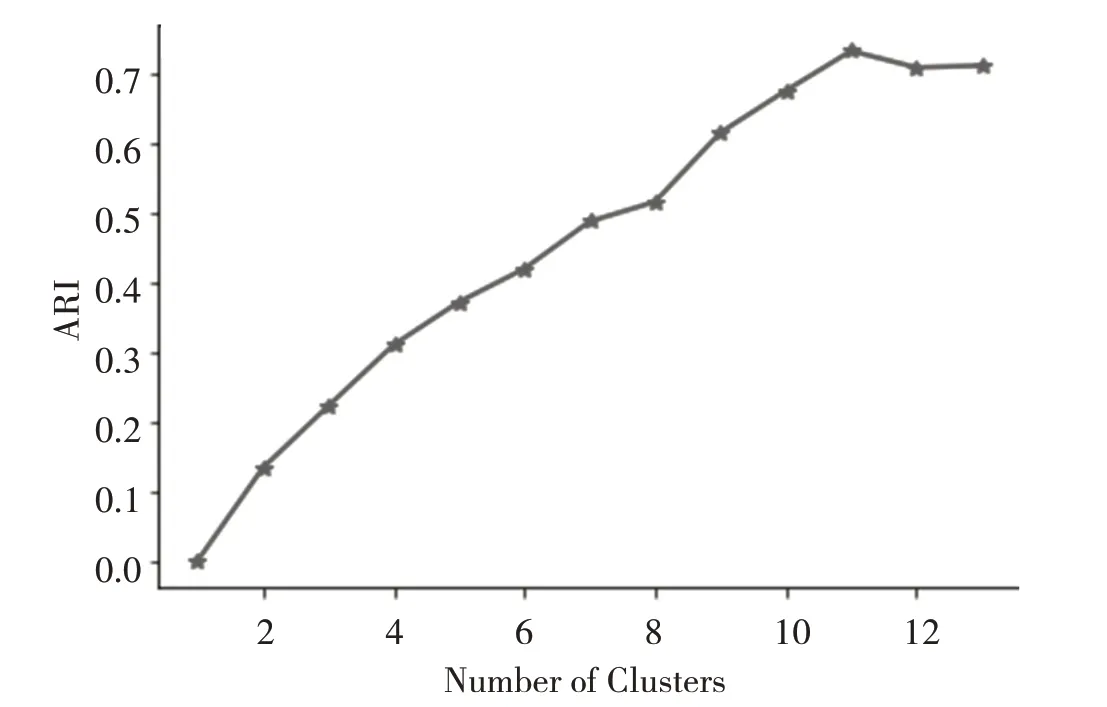
图7 ARI指数关系曲线

图8 轮廓系数关系曲线

关于两条曲线之间的差异：比较两张图的差异，ARI指数在k=11时呈现拐点，而轮廓系数指数在k=9时呈现拐点。ARI是一种外部方法，主要用于评估分类模型的性能，而轮廓系数是一种内部方法，主要用于通过检查簇的分离度和簇的紧密度来评估聚类。因此，两种方法在评估聚类效果时可能存在一些差异。在本实验中，显然主要目的是通过聚类算法可以分类出不同的人，在两种指标有冲突的时候，对于本实验，更看重ARI指标。由图中可以看出，ARI在当簇等于11时出现拐点，所以，聚类评判标准验证的结果是，当聚类数目为11时，聚类效果是最佳的。由测试集得知，共有13个人参与到贡献测试集，也就是说，实验结果和真实值相比较，差距较小，实验结果达到理想状态。

最后，为了生成可视化的聚类效果图，分别将上述聚类后的数据进行归一化，并降维，在处理数据的过程中，簇类数目设置范围从8到13，分别以不同的样式进行绘图，结果如下图所示。

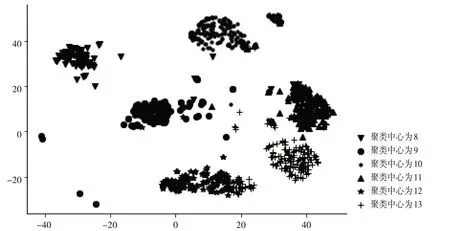
图9 聚类效果图

在图片上，“*”状散点图的离群点和噪声值较少，紧凑度一般；“o”状散点图紧凑度虽然很好，但是离群点太多；“.”状散点图离群点虽然少，但是紧凑性差。综合来看，“*”状散点图和“^”状散点图的聚类效果都很好，其中“^”状散点图对应的聚类中心是11，而“*”状散点图对应的聚类中心是12.由此可见，通过可视化分析后，得出的结论和之前通过评价标准得出的结论是差不多的，精准度依然很高。在实验设计上，如果可以根据数据密度或者是提前已经明确的数据密度分布，或许可以先给出数据的初始质心，这样后续得出的聚类效果会更好。另一方面，如果训练集的数据量尽可能大，还可以让聚类模型更详细地获取数据点的整体特征、一些异常值和噪声信息，最后得出的聚类中心数也会更加逼近真实值。

尽管手写数字识别算法的研究往往集中在一些以前的分类和神经网络算法，如CNN、SVM等，但现在聚类算法也可以用于手写数字识别。虽然准确率还有待进一步提高，但笔者相信随着大数据的普及应用，通过对大量数据的训练，对于手写数字识别，聚类算法的准确率也会有很大的提高，这也是未来研究的重点。

7 结语

文章首先通过K-means聚类算法对手写数字进行聚类分析，同时探讨聚类算法在手写数字识别的可行性，并进一步探讨其准确率。在通过一些聚类指标进行评价时，可能会出现结果异常的情况，这个时候，需要将聚类结果进行降维并可视化分析，再将可视化分析后的聚类结果与评价指标得出的结果进行验证，最后得出比较可靠的结论。比如，在本实验中，通过ARI和轮廓系数得出的聚类中心数目大致是11和9，后续通过降维并可视化得出的结论是11或12，这样可以相互验证两边的结论。当数据量出现大幅度增长时，串行K-means聚类算法是否还能达到这样的精准率，尚未可知，如若不能达到本实验的精准率，则可以利用大数据处理平台Hadoop或spark平台对K-means聚类算法实施并行化。并行化相对于串行化可以大大增加算法的算力，在增加算力的基础上，通过多节点的设置，可以大大缩短处理图像或文本的时间，从而可以提高算法的精准率。

手写数字识别的研究意义重大，这一领域有望拓展到笔迹识别问题的研究，特别是一些没有明显特征点的笔迹识别问题，可以在笔迹上提取一些少量的特征点，并编码，形成多维矩阵，通过这些多维矩阵识别手写签名；同样，中文签名需要从笔画来识别。汉字有五种典型笔画：横、竖、撇、笔、勾。鉴于手写数字和五笔相似的特征点，未来通过大规模的机器学习，在建立聚类算法模型之后也应该能识别出一些简单的中文。