含参数偏微分方程的Greedy-KPOD模型降阶
2022-12-24邢秩源蒋耀林
邢秩源,王 丽,蒋耀林,2
(1.新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046;2.西安交通大学数学与统计学院,陕西 西安 710049)
1 引言
在众多诸如控制、力学、流体机械等工程领域,都涉及复杂系统的计算机仿真、优化与控制,而这类系统的模型大多通过偏微分方程来建立。通过对相应的偏微分问题进行相当精细的模拟求解,可以为实际工程提供安全、高效的数据。随着高性能计算机的快速发展,偏微分方程的数值求解方法,如有限差分法,有限元法、有限体积法、谱方法等得到了普遍应用。实际工程模型的复杂性决定了这些偏微分方程的数值离散系统的规模十分庞大,这使得单纯采取数值方法求解复杂和长时间尺度的偏微分方程具有较大局限性,在有限计算资源条件下往往得不到理想的数值模拟效果。模型降阶方法[1]能够利用低维模型去逼近原高维模型,获得较低计算代价下的可接受降阶模型,极大地节约计算资源和提高模拟效率。因此偏微分方程的模型降阶方法是很重要的研究课题。
模型降阶方法在很好地近似高维系统解的同时还能保持原高维系统的一些重要特征,如稳定性、结构特性等。随着模型降阶方法理论的成熟,其在许多工程领域中发挥着越来越重要的作用,也因其具有高效快速的计算性能被逐渐应用到偏微分方程的求解中,如本征正交分解模型降阶方法[2,3](POD, Proper Orthogonal Decomposition)、Krylov子空间模型降阶方法[4]、平衡截断模型降阶方法[5,6]和黎曼优化模型降阶方法[7,8]等。POD方法是用低维数据信息来近似高维数据信息的一类常用的降阶基方法,该方法已广泛应用于各类非线性系统。对于含参数偏微分方程,由于方程系数及相应的解随着参数的变化而不断改变,直接用传统模型降阶方法(如POD)求解并不能达到期望的求解效果,故对参数进行预处理是很有必要的。Peter Binev等人通过Greedy算法及Kolmogorov宽度对含参数偏微分方程进行降阶求解,并验证了该方法的收敛速率[9]。Haasdonk等人提出了含参数偏微分方程的Greedy-POD降阶基方法,分析了该算法的收敛性[10]。文献[11]进一步阐述了降阶基空间的构造,分析了先验和后验误差,并验证了该方法对含参数偏微分方程求解的有效性。
本文进一步提出含参数偏微分方程的Greedy-KPOD模型降阶方法。该方法建立在Krylov enhanced POD (KPOD)方法[12]和Greedy 参数优化算法取样的基础上,结合Galerkin变分理论及参数分离方法而提出。同时,给出单边及双边Greedy-KPOD方法的具体算法格式。所提出方法具有原始问题参数结构和较高的计算精度,且相比传统Greedy-POD方法具有更少的计算复杂度。
2 含参数的Galerkin变分离散系统
设T>0,Ω∈Rd(d=1,2,3)为连通区域,边界∂Ω为分段光滑的,μ∈P,其中P⊂R是参数空间。考虑如下含参数偏微分方程
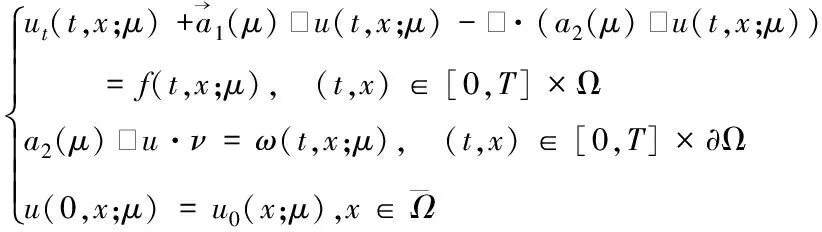
(1)

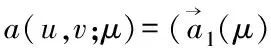
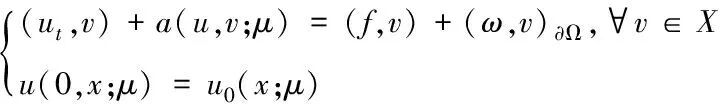
(2)
成立。选取标准连续有限元空间Xh:= span{φ1(x),φ2(x),…,φN(x)},则方程(2)的空间有限元离散的Galerkin逼近为:对∀t∈[0,T],求uh∈Xh⊂X有

(3)
成立,其中uh0表示初始条件u0(x;μ)在离散空间Xh中的插值。对于任意μ∈,t∈[0,T],方程(3)的解uh(t,x;μ)可以用有限元基函数φi(x), (i=1,2,…,N)来逼近,从而得到方程(3)的N个含参数微分方程,其简化的矩阵形式为
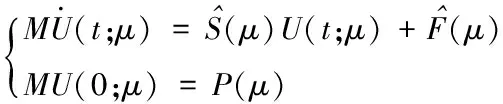
(4)
3 参数系统的Greedy-KPOD模型降阶方法
对于参数微分方程,执行Greedy-POD方法时需要生成大量快照点并进行矩阵分解,其计算规模是很大的。为此,提出单边及双边Greedy-KPOD模型降阶方法来降低大规模矩阵分解的代价。
3.1 Greedy 参数优化算法
Greedy算法于70年代早期被引入以来,已被广泛地应用于优化等问题[13]。该算法是一种通过迭代来选择最优样本点的参数优化算法,即在满足一定条件的情况下,逐步迭代选出最优参数。具体地,在迭代过程中假设给定参数集
H={μ1,μ2,…,μJ},H⊂P
在H中,近似误差‖u-Vuh‖Xh与后验误差Δn(μ)满足如下关系
‖u-Vuh‖Xh≤Δn(μ),∀μ∈H
其中u为原始系统的解,uh为有限元离散解,V为离散函数空间到连续函数空间的投影。每次迭代都在剩余参数集中选择使后验误差最大时对应的参数,故对∀μ∈H,迭代过程中每步都需要计算后验误差。
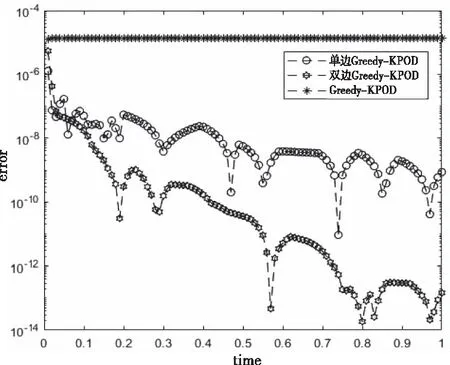
假设已选出n个参数μi,i=1,2,…,n,其中n 且 其中0<εg≤1为给定的正定充分小的临界值。 随着模型降阶方法的应用越来越广泛,其理论因实际问题的需求而不断完善。其中KPOD模型降阶方法的核心是基于系统传递函数的矩匹配特性构造Krylov子空间,进而通过与POD方法结合构造降阶所需的变换矩阵。该方法比单纯POD方法有更低的计算复杂度。 为便于讨论,仅考虑零初始状态及齐次的情况,即u0(x;μ)=0及F(μ)=0。定义系统(4)的输出Y(t;μ)∈Rp及输出矩阵C∈Rp×N。则有如下输入输出参数系统 (5) 对于参数系统(5),根据Greedy算法选定的参数μi,i=1,2,…,n,得到对应的原始系统的传递函数 H(s;μi)=C(sM-(μi))-1R(μi) 设S(μi)非奇异,将H(s;μi)在s=0处Taylor展开为 故原始系统的传递函数H(s;μi)在s=0处的第j阶矩为 ml(μi)=-C((μi)-1M)l(μi)-1R(μi) (6) 类似地,投影系统的传递函数在s=0处的第l阶矩为 (7) 下面针对参数系统(5),提出如下单边及双边KPOD模型降阶方法。 3.2.1 单边KPOD模型降阶方法 对于单边KPOD模型降阶方法,首先利用系统的输入信息,构造输入Krylov子空间Kk((μi)-1M,(μi)-1R(μi))。其次,通过块 Arnoldi过程得到一组正交基矩阵=[(μ1),(μ2),…,(μn)]∈RN×(pkn),利用可得如下投影系统 (8) 证明:因为矩阵 (μi)-1M∈Kk((μi)-1M,(μi)-1R(μi)) 根据式(7)和式(8)可以得到 m0(μi)=-CT(T(μi))-1TR(μi) =-CTξ0=-CT(μi)-1R(μi)=M0(μi) ((μi)-1M)l(μi)-1R(μi)=ξl 成立。为证明此结论,用归纳法可证明下式成立 ((T(μi))-1TM)l(T(μi))-1TR(μi)=ξl (9) 类似于文献[3]中的证明,有 ml(μi)=-CT((T(μi))-1TM)l(T(μi))-1TR(μi) =-CTξl=-CT((μi)-1M)l(μi)-1R(μi)=Ml(μi)故ml(μi)=Ml(μi),l=0,1,…,k-1。证毕。 3.2.2 双边KPOD模型降阶方法 双边KPOD模型降阶方法是利用系统的输入及输出信息分别构造输入Krylov子空间Kk((μi)-1M,(μi)-1R(μi))及输出Krylov子空间Kk((μi)-TMT,(μi)-TCT)。进而分别得到输入、输出Krylov子空间的正交基矩阵=[(μ1),(μ2),…,(μn)]及=[(μ1),(μ2) …,(μn)],令V=[,]∈RN×2pkn。 证明:由于矩阵 因此存在一个矩阵ζl∈2kn×p满足((μi)-TMT)l(μi)-TC=Vζl,l=0,1,…,2k-1等价于进而,可以得到 CTV((VT(μi)V)-1VTMV)l =(CT(μi)-1)(μi)V((VT(μi)V)-1VTMV)l =CT((μi)-1M)l-1(μi)-1MV =CT((μi)-1M)lV 此外,根据定理1可得 V((VT(μi)V)-1VTMV)k-1(VT(μi)V)-1VTR(μi) 因此,当l=k,k+1,…,2k-1时,由定理1的证明过程可得ml(μi)=Ml(μi),l=0,1,…,2k-1,即匹配原始系统的前2k阶矩。证毕。 在Greedy算法的迭代过程中,每次都要计算剩余参数集中参数所对应的后验误差Δn(μ),因此降低后验误差的计算复杂度是很有必要的。 在参数系统(5)中,由于该系统的系数矩阵S(μ)、L(μ)及R(μ)与参数μ相关,随着参数的变化每次降阶都要在原始大规模系数矩阵上进行,这无疑增加了降阶过程的计算复杂度。故在降阶前,首先对参数进行分离,将含参系数矩阵通过近似的方式分离为参数部分与非参数部分,即 其中Sq∈RQ×Q、Lq∈RQ×Q及Rq∈RQ×Q,q=1,2,…,Q,分别表示S(μ)、L(μ)、R(μ)在点μ0处的近似Taylor展开系数矩阵。然后将上式代入原参数系统(5)中,得到近似参数系统为 (10) (11) 算法1:单边Greedy-KPOD模型降阶方法 输入变量:系数矩阵M,q,Rq,C;参数样本集H⊂;迭代临界值Nm;误差临界值εg;降阶阶数r;初始参数μ1∈。 输出变量:变换矩阵Ψr和降阶系统的系数矩阵Mr,qr,Rqr,Cr。 1)n=0,δ0=1 2)Dowhilen≤Nm且δn>εg 3) 令n=n+1 B(μn)=-1(μn)R(μn) 5) 对输入Krylov子空间Kk(A(μn),B(μn))实施块Arnoldi算法得基底矩阵∈RN×pkn,对奇异值分解得到正交阵Φ 7)Ψr=[ΨrΦ],并对Ψr进行QR分解得到Γ 8) 截断Γ的前r列得到Γr,并令Ψr=Γr 9) 令H=H∪{μn} 10)fori=1:length(H) 11) 利用Ψr得到降阶解 12) 计算后验误差Δn(μi) 13)endfor 16) end while 为了进一步利用输出矩阵信息,在单边Greedy-KPOD算法基础上给出下列双边算法。 算法2:双边Greedy-KPOD模型降阶方法 输入变量:系数矩阵M,q,Rq,C;参数样本集H⊂P;迭代临界值Nm;误差临界值εg;降阶阶数r;初始参数μ1∈P。 1) 执行算法1得到单边Greedy-KPOD方法的变换矩阵Ψr 2) 类似算法1第5步构造输出Krylov子空间Kk((μi)-TMT,(μi)-TCT),得到基底矩阵,并对其奇异值分解得到 注意到,双边Greedy-KPOD降阶系数矩阵的构造将依赖当前计算的参数点,即对不同参数点降阶时需要进行上述几步预处理,因此计算复杂度相比单边算法略大一些。 下面验证Greedy-KPOD模型降阶方法对含参数偏微分方程的可行性及优势。 设T∈[0,1],Ω=(0,1),P⊂[0.8,1],给定40个参数。考虑如下零初始状态的含参数偏微分方程 (12) 设a1(μ)=2μ+1,a2(μ)=5μ+1,边界条件为[ω1,ω2]=[100,0.1]。 对空间Ω等距剖分,离散自由度为N。通过Galerkin有限元离散,得到方程(12)的含参数微分方程组,根据输出矩阵C,进一步得到形如系统(5)的矩阵形式。 在参数集合P内随机选取参数μ=0.897,基于算法1和算法2,分别得到N=100,N=500,N=1000阶降至r=13阶的降阶系数矩阵。进而得到降阶解与有限元解的相对误差。同时采用Greedy-POD方法作为对比,在迭代中计算前1/5时间区间的解构成快照集合。图1、图2、图3分别为N=100,500,1000时,单边Greedy-KPOD,双边Greedy-KPOD与Greedy-POD方法所对应的降阶解与有限元解的相对误差。由图1-3可以看出,当N较大时,单边及双边Greedy-KPOD方法相比传统Greedy-POD方法的降阶效果优势更明显。此外,结合多次计算结果的精度比较,双边Greedy-KPOD方法在一些参数点处比单边Greedy-KPOD方法更具精度优势,但单边Greedy-KPOD方法相比双边Greedy-KPOD方法的降阶效果更稳定。 图1 N=100时的相对误差 为了说明降阶矩阵生成过程的优势,表1给出了上述情况下三种模型降阶方法生成变换矩阵所需的时间。从表1可以看出,随着原始系统规模增大,在具备精度优势的前提下,两种Greedy-KPOD方法相比传统Greedy-POD方法生成变换矩阵所需时间少很多,且双边Greedy-KPOD比单边Greedy-KPOD方法耗时略多一些。所以本文所提方法在降低计算复杂度方面更有优势。 图2 N=500时的相对误差 图3 N=1000时的相对误差 表1 生成变换矩阵所用时间 本文研究了含参数偏微分方程的Greedy-KPOD模型降阶方法,提出了基于块 Arnoldi 过程的单边及双边 Greedy-KPOD 模型降阶算法,主要结论有: 1)所提方法使得降阶系统能够保持原始系统的参数结构; 2)数值算例给出了所提方法对应的降阶解与有限元解的相对误差,与传统 Greedy-POD 方法相比具有更好的降阶效果; 3)实际应用单边和双边 Greedy-POD 方法时,如果在计算时间和稳定性上有更高要求,则应用单边 Greedy-KPOD 方法;如果问题的输出矩阵相对复杂和重要,可以应用双边 Greedy-KPOD 方法,从而获得更好的近似精度; 4)相比传统 Greedy-POD 方法需要生成大规模快照矩阵并进行分解方式,基于 KPOD 方法进行最优参数迭代,生成变换矩阵的用时更少,因此有望通过改善后应用于实际的大规模对含参数偏微分方程求解问题。
3.2 参数系统的KPOD方法

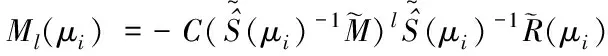
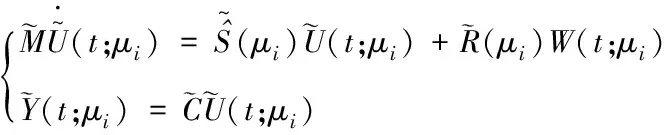

3.3 Greedy-KPOD模型降阶方法



4 数值实验
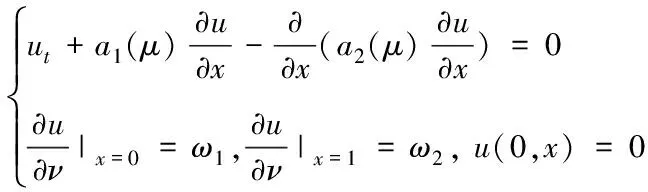



5 结论
