基于信息熵及专家群决策的失效模式风险评估

张家贤，余 洪，涂继亮

(1.南昌航空大学信息工程学院，江西 南昌330063；2.江西洪都航空工业集团有限公司，江西 南昌330024)

1 引言

风险优先数(Risk Priority Number，RPN)作为一种有效的失效模式风险评估方法目前仍被广泛地使用，比如文献[1]中利用风险优先数结合Dempster-shafer理论对主机曲轴箱爆炸事故进行风险优先评估。这种方法需要专家组针对各种失效模式的严酷度(S)、发生度(O)、难检度(D)三个风险因子进行评估，将该种失效模式下三种风险因子的评估结果融合后即可得到该失效模式的RPN值，然后依据每种失效模式的RPN值进行排序即完成了对所有失效模式的风险评估。这种方法的优点是高效易行，但是相对应的缺点也很明显[2]：评分制严重依赖于专家组成员的经验与个人观点，会造成评估结果的不客观性；专家对于某一个问题的看法受到环境的影响很大，对待同一个问题专家每次给出的结果也许会不一样，这会造成评估结果的不稳定性。在不同失效模式下存在三个风险因子的分值不同，但是经过乘积以后的RPN值却相同的情况，这样就无法区分故障模式的风险优先顺序。

为了解决上述问题，国内外的许多专家都对这种失效模式评估方法做出了改进。Wang[3]等利用风险优先数结合层次分析法获得各风险因子的相关权重，利用物元拓展模型计算各失效模式的接近系数，从而确定各失效模式的风险排序。陶秋香[4]等筛选出专家的重要性量化指标，计算出各专家权重，然后组织专家对风险因子进行重要度评价及信度分析，根据未确知集理论计算各风险因子的权重，提出了基于未确知集和模糊TOPSIS决策的故障模式风险评估方法。但是该方法通过外在的量化指标确定专家权重，并不是基于数据本身来确定的，而且专家组仅仅对风险因子进行了群决策，而忽略了对故障模式的群决策。李丽颖[5]等以某指标的评价值与其它方案中同一指标的评价值的偏差为度量，结合区间三角模糊数(集)的海明距离计算各属性的权重，最后依据各方案与最优解的相对贴近度来进行排序。该方法是根据各属性的变异程度来确定该属性的权重，如果变异程度小相应的属性权重也小，但是这对于某些小概率但是影响却非常大的模式不能进行客观的排序。聂文滨[6]等根据模糊区间的数据分布，结合广义豪斯多夫距离来评价各专家评估意见之间的相似度，进而确定各专家的权重与故障模式的风险排序。该方法需要计算置信区间的均值、方差和概率密度函数，过程非常繁琐。Mohammad Yazdi[7]针对模糊综合评价过程中存在的不确定性，分别利用层次分析法和熵权法处理主观与客观不确定性权重，减轻了模糊性与不确定性对常规的失效模式与风险评估的影响。

上述方法均引入模糊理论来改进传统的失效模式风险评估方法，这很好的契合了失效模式间的相似性与专家评价的经验性和模糊性的特征。本文在上述文献的基础和不足上提出了一种基于信息熵和专家群决策的失效模式风险评估方法。首先将专家组成员对失效模式及风险因子的评价转换为模糊评价矩阵，根据每种风险因子评价矩阵的信息量和专家意见的贴近度来确定各专家的权重，然后将各专家评价意见经过信息融合以后得到专家群决策模糊矩阵，进而得到各失效模式的风险优先数，从而实现了对失效模式的风险排序。应用实例说明了该方法的具体实现过程，验证了其有效性和可行性，并进行了敏感性分析。

2 基于模糊数的专家评价信息处理

2.1 专家评价信息的处理

在经过专家组的讨论确定失效模式的种类与数量之后，采用问卷调查的方式对每位专家组的成员进行调查，每位专家组的成员依据自己的评价体系对每种失效模式的严酷度、发生度和难检度进行评价。评价结果采用[0 10]的区间数结合专家个人的乐观系数η(0<η<1)来决定，其中区间数[xy]代表该种失效模式下的相应风险因子的重要(严重)程度，区间数越大表示该种失效模式越重要(严重)。乐观系数η体现了专家评价语言变量的模糊性，η越小表明该专家对当前失效模式的重要(严重)程度越乐观。根据专家的评价语言结合乐观系数，可以将每位专家的语言评价转换为三角模糊区间数。具体的转换公式为

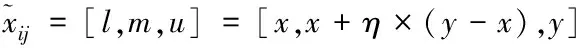
(1)

例如当某种失效模式在严酷度下的专家评价语言变量为[4 5](η=0.1)，则该语言变量转化为三角模糊数为[4，4.1，5]。组织k位专家组成专家组对m种失效模式进行风险评估，按照上述方法将每位专家的语言评价变量转换为三角模糊数，最终得到3个m×k的三角模糊评价矩阵。

文献[8]根据三角模糊数[l，m，u]的隶属函数将三角模糊数划分为均匀分布型和比例分布型两种。当η=0.5或l=u时该语言变量所对应的三角模糊数为均匀分布型，反之为比例分布型。均匀分布型的三角模糊数的均值为

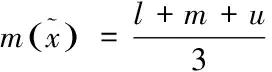
(2)

比例分布型的三角模糊数的均值为

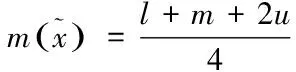
(3)

三角模糊数[l，m，u]的信息量反映了专家在自己的评价体系下对未来可能发生的失效模式的评估，信息量的计算公式定义为[9]

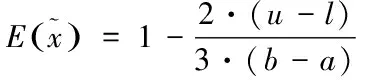
(4)

式中：a和b在本文中分别为0和10。

评价语言的信息量越大，则代表该专家在未来能够补充的信息量越多。如果一位专家提出了不同的意见，则代表该专家的评价信息所包含的信息量非常多。如果专家的意见太过超前又会导致得不到其他专家的认同。

定义：为了体现在决策过程中“既有民主又有集中”的思想。本文提出基于传统信息量结合专家意见贴近度的信息熵计算公式

那天，下着小雨，父亲用独轮车推着床、席子、被子、脸盆，用塑料布盖好，走了二十多里，在学校的路上等了两节课。父亲身上的旧雨衣也不挡雨，头发衣服都湿了，满脸满身的雨水。我赶紧把东西拿到宿舍，让父亲吃午饭再走，可父亲说回去还有事，又推着独轮车回去了。

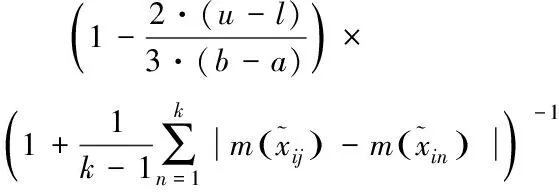
(5)

式中：i为第i种失效模式，j为第j种风险因子，p为第p个专家，k为专家的总数。

2.2 专家权重的确定

每位专家的权重依赖数据本身的信息熵来确定，而不是依赖专家本身的职称和其它的外部条件。信息公理指出评价语言的信息熵越大，则该评价目前所包含的信息量越小但是在未来能够补充的信息量却越大，相应的该方案就更加的重要[10]，但是如果这位专家的评价信息又得不到其他专家组成员的认可，则该专家的权重又相应的需要减小，本文所述方法能够同时考虑到上面两种情况，这样既能够保留专家组成员的主流意见又能够听取那些有独特见解的专家的意见，符合对待重大问题的“集中讨论，个别酝酿，集体决定”的原则。本文根据信息熵来衡量每位专家的权重，对每位专家的评价信息熵进行归一化后，可得每位专家在不同风险因子下的权重为

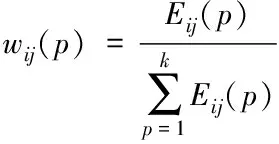
(6)

2.3 专家评价信息的融合

将每位专家在当前失效模式下的权重乘以对应的失效模式评价矩阵，即可得到每位专家对所有失效模式的三角模糊评价矩阵，将每位专家的评价矩阵按照模糊信息融合理论进行融合，即可得到最终的专家群决策矩阵

(7)

3 工艺失效模式的RPN评估实施程序

总结上述研究过程，现给出基于信息熵及专家群决策的失效模式风险评估方法的主要步骤：

1)组建专家组，确定待评估的失效模式FMi(i=1，2，…，m)，收集专家组对三种风险因子的评价信息。

2)按照式(1)的转换方法，将每位专家的语言评价变量转换为三角模糊数。将所有专家对同一个风险因子评价信息转换为三角模糊评价矩阵。

3)将风险因子的三角模糊评价矩阵按照式(5)的方法计算每位专家评价语言的信息熵，按照式(6)将同一种失效模式的信息熵归一化后即可得到每位专家的权重。

4)根据专家的权重对风险因子的三角模糊评价矩阵进行加权平均。对加权三角模糊评价矩阵中每一种失效模式的评价信息进行加法融合，即可得到该风险因子的专家群决策矩阵。

5)按照模糊信息融合理论将三个风险因子的评价矩阵融合即可得到基于专家群决策的失效模式模糊风险优先数矩阵，融合方式如下

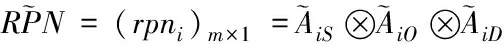
(8)

6)考虑三种风险因子的权重，将失效模式模糊风险优先数矩阵按照均值方法去模糊化后进行排序。排序越靠前，表明该失效模式越重要。

该方法的流程图如图1所示。

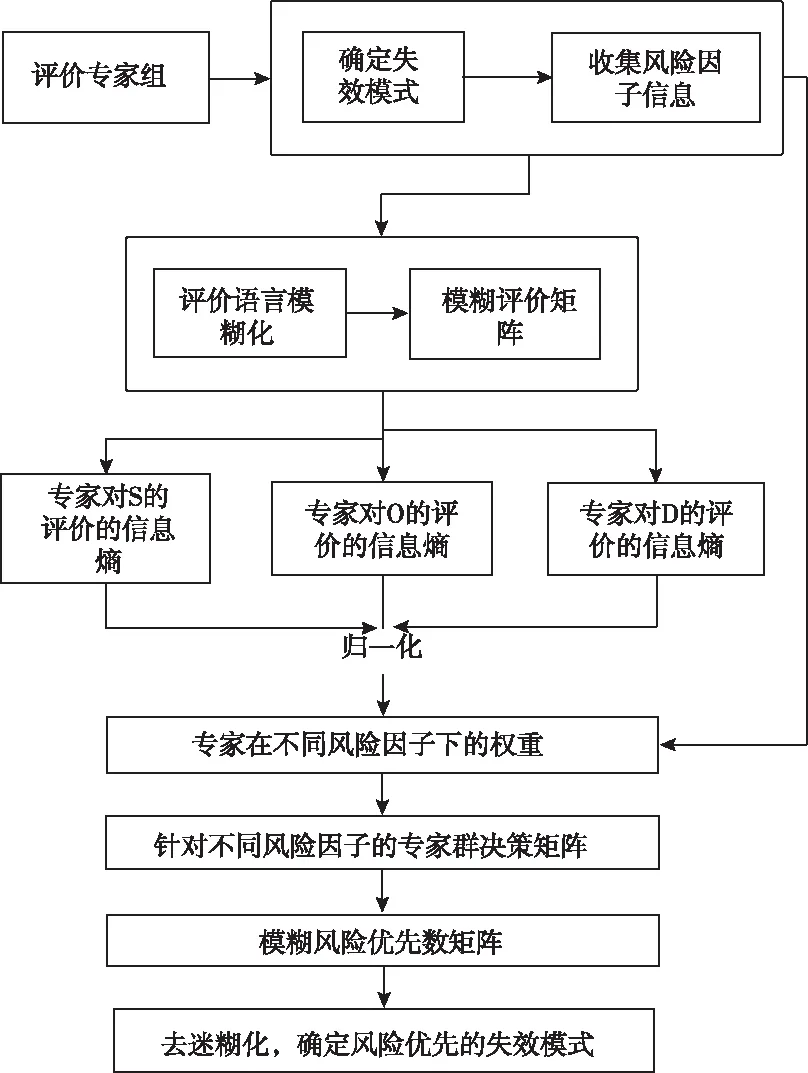
图1 算法流程图

4 应用实例验证

为了验证本文提出的基于信息熵及专家群决策的失效模式风险评估方法的有效性与可行性，本文以文献[6]中飞机方向舵舵机安装工艺失效模式风险评估作为应用实例，按照上述方法进行失效模式风险排序。由文献[6]中表3和表4数据及本文式(1)得到5位专家对严酷度、发生度、难检度的模糊评估矩阵如表1所示。

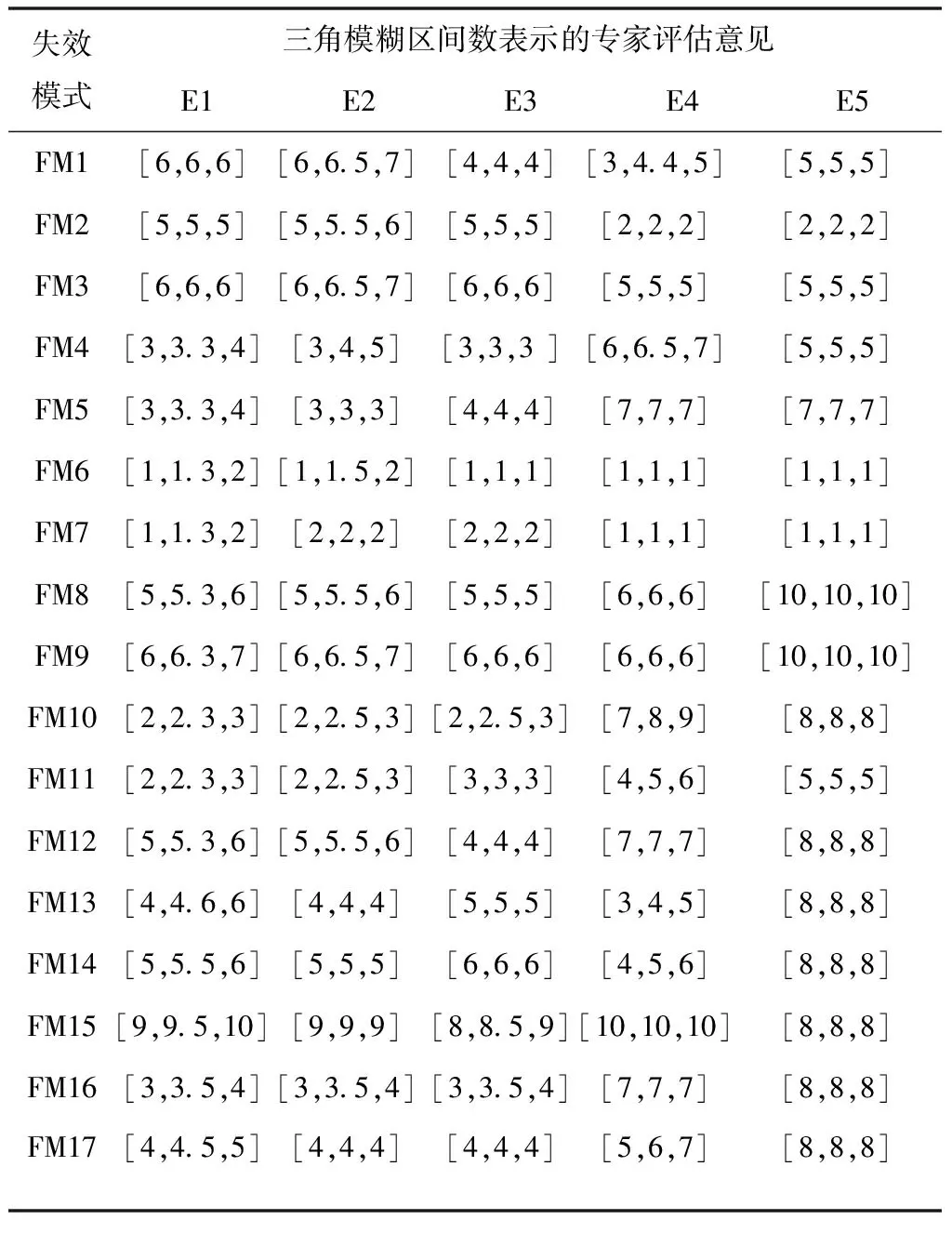
表1 五位专家对严酷度S的模糊评价矩阵

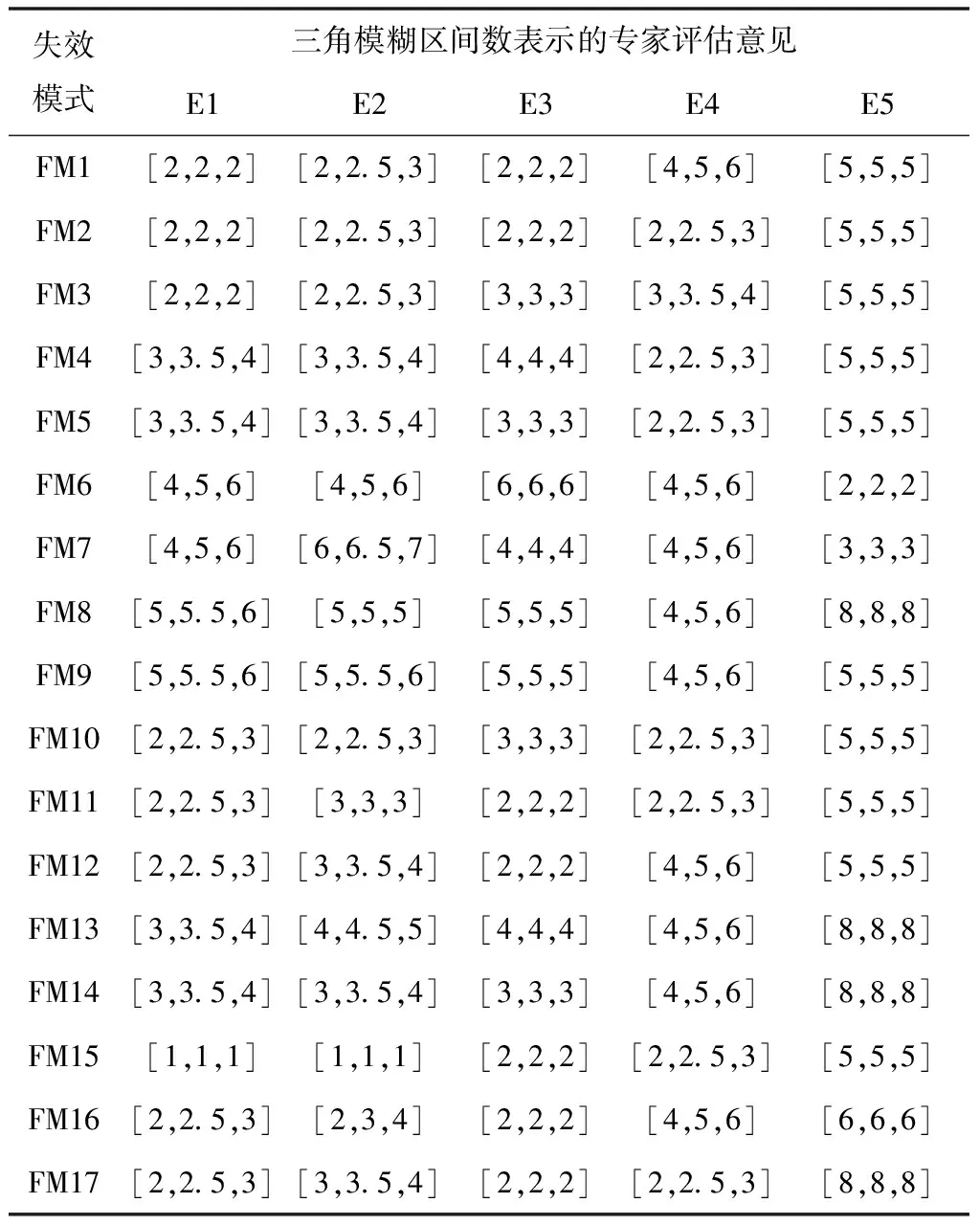
表2 五位专家对发生度O的模糊评价矩阵

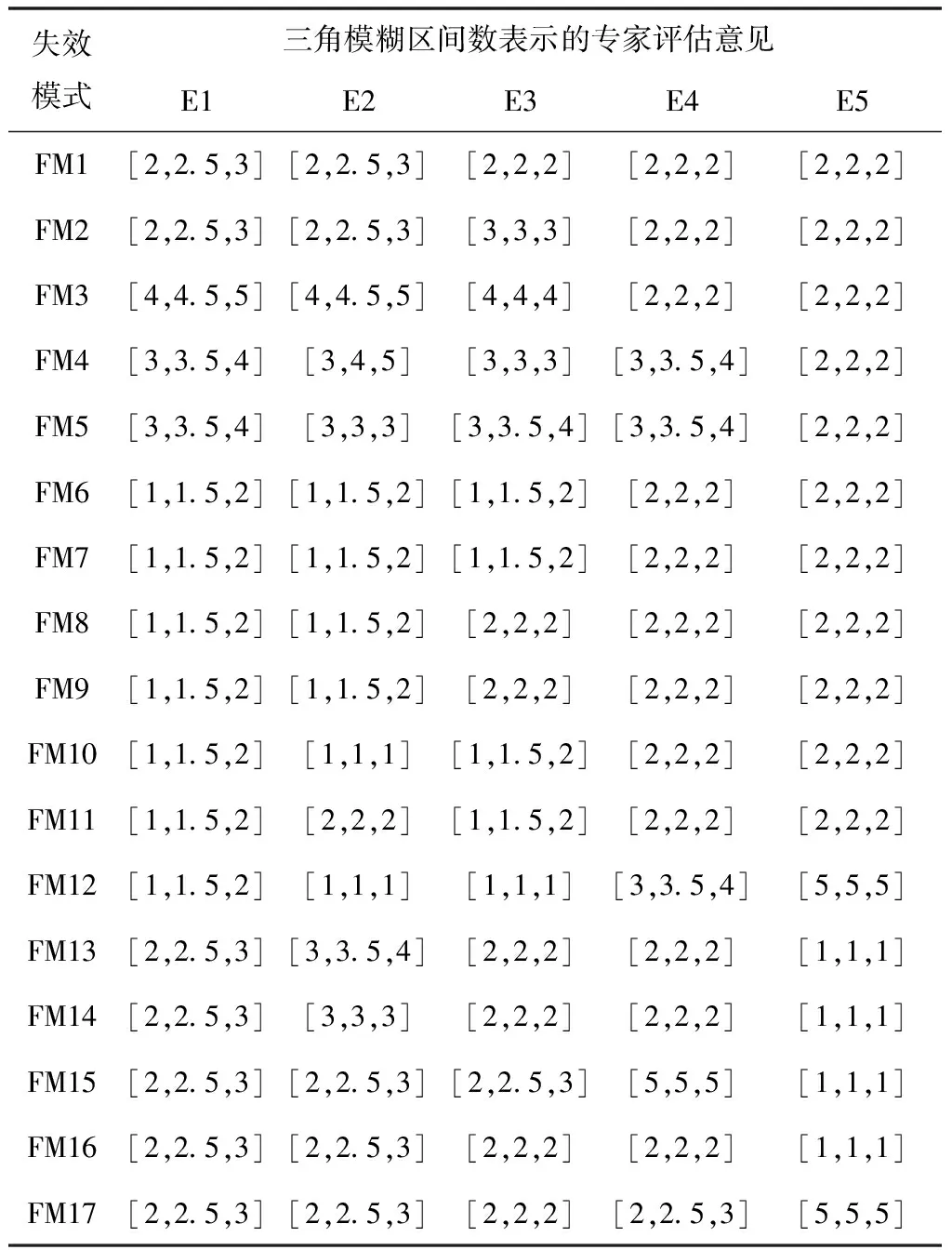
表3 五位专家对难检度D的模糊评价矩阵

运用式(2)、式(3)、式(5)、式(6)计算出每位专家在不同风险因子下对各种失效模式的权重，运用式(7)对三角模糊评价矩阵进行加权平均，对同一种失效模式进行加法信息融合即可得到专家群决策矩阵，运用式(8)即可得到模糊风险优先数矩阵。考虑到在实际运用过程中，严酷度、发生度、难检度的权重可能会不一样，本文分别将它们取为0.3、0.25、0.45。依据式(3)、式(4)求出精确的RPN值，然后对各失效模式进行风险排序，结果如表4所示。

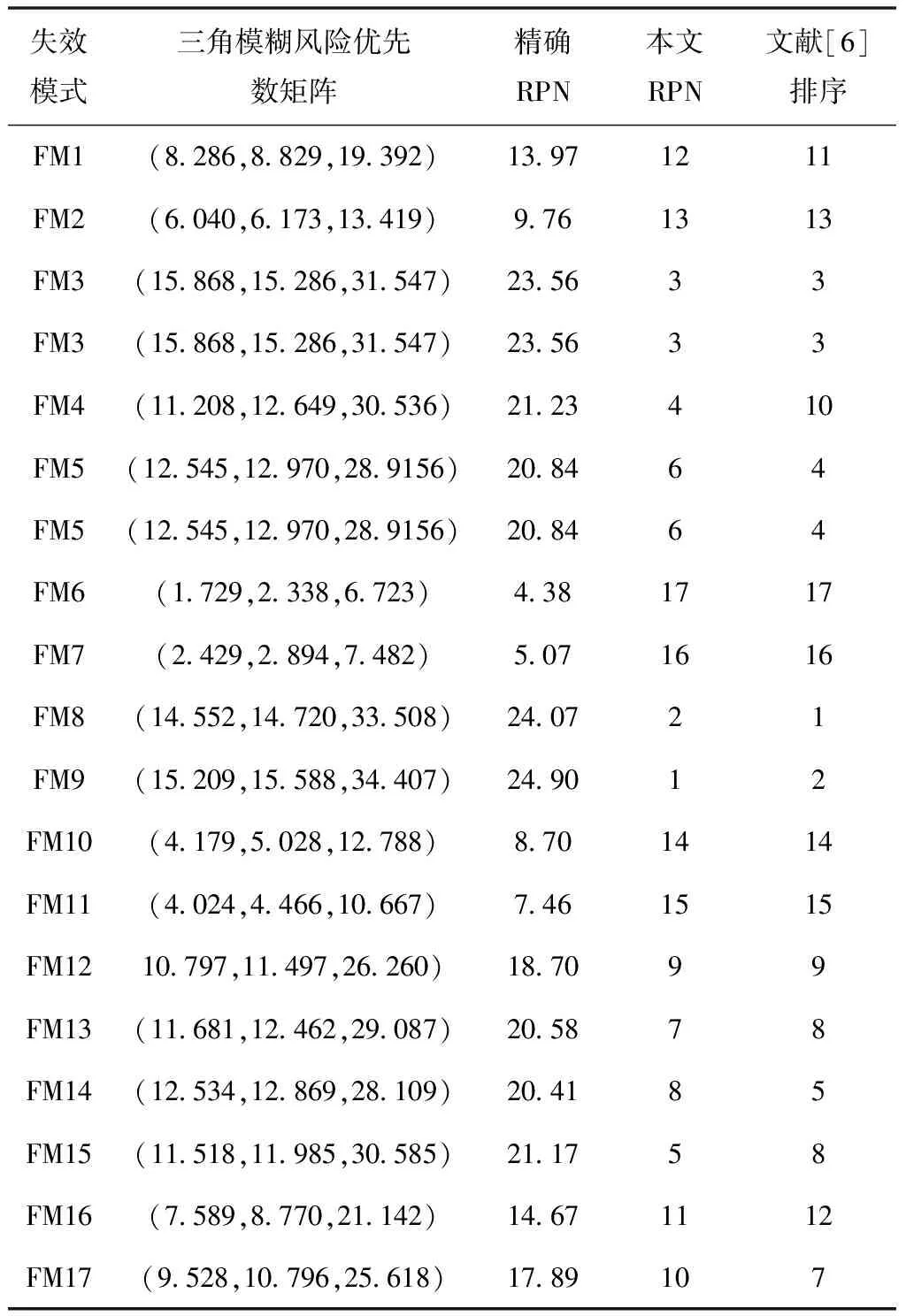
表4 各失效模式的风险排序

从表4可知本文所述方法得到的结果较文献[6]所得到的结果有较大调整，结果差异率为58.8%。主要原因是本文利用评价语言的信息熵对专家的权重进行了修正，并且考虑到了风险因子的权重，但是文献[6]中并未考虑。此外，文献[6]得到的优劣区间贴近度的数值都很接近，而本文得到的RPN值的辨识度很高，能够帮助决策人员显著区分各种失效模式。

为了验证基于信息熵及专家群决策的失效模式风险评估方法的稳定性，依据表5的风险因子权重信息对该方法进行敏感性分析，得到的结果如图2所示。由结果可知在5次实验中，排在前3级的失效模式并未发生改变，只有第4次实验的FM5、FM13、FM14、FM15的风险等级各调整了1级，不稳定性仅有5.88%。由此可知，该方法对风险评估过程中的变化较不敏感，具有良好的可靠性与适用性。

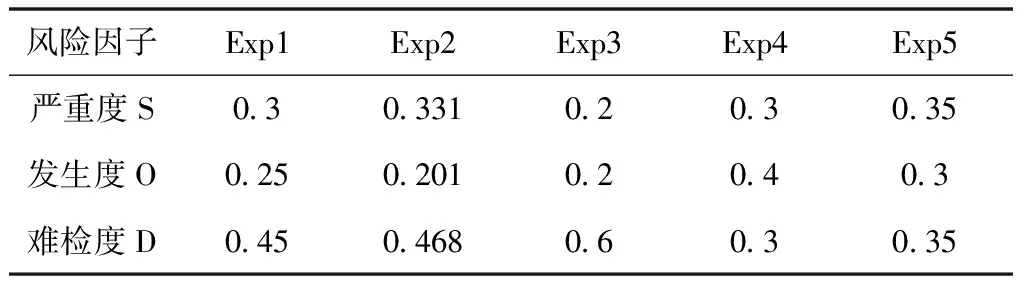
表5 敏感性分析中风险因子的权重

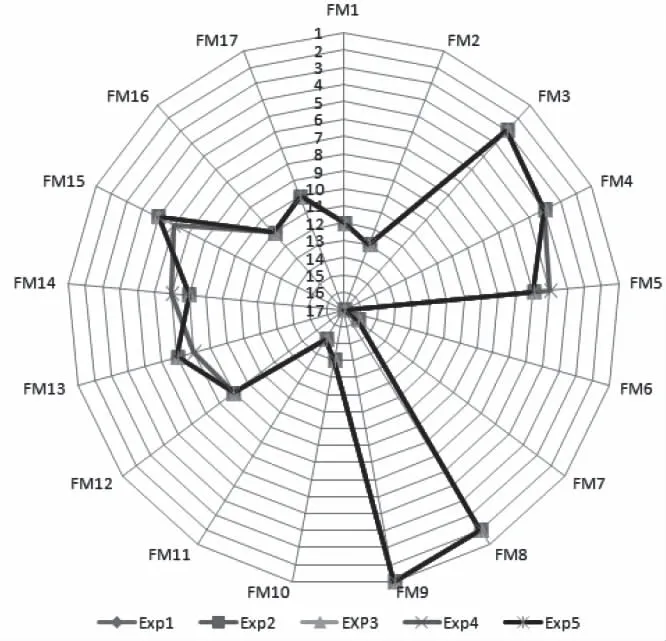
图2 敏感性分析结果

5 结束语

本文根据信息理论和模糊理论提出了基于信息熵及专家群决策的失效模式风险评估方法。根据专家评价语言变量所包含的信息量的大小来判断该专家在专家组相应权重的高低，结合专家评价语言的贴近度综合考虑每位专家评价语言的信息熵，客观合理地计算每位专家的权重。在进行去模糊化时考虑到不同三角模糊数的类型，选择不同的去模糊化方法，这样能够得到更加精确的风险排序结果。综合来看本文所述方法具有如下优势：

1)由乐观系数体现专家在进行风险评估时的模糊性，能够最大程度的保留专家的个人意见，符合人类思维的多样性与发散性的特点。

2)综合考虑专家评价语言的信息量与相对于其他专家的贴近度，充分保留每位专家的专业背景、知识结构与实践经验。即避免评价信息的缺失又保证了评估过程的可靠性。

3)本文所述方法实现过程简单，结果稳定，并且可以根据实际的需求改变风险因子的权重，能够应对现实环境中各种复杂的情况。

本文所诉方法虽然弥补了风险优先数法的一些缺陷，但仍具有一定局限性：

1)通过模糊理论中的方法得到精确值会丢失一些模糊数据的评价信息，因此在未来的研究中可考虑采用二元语义的方法避免去模糊化过程中评价信息的丢失。

2)虽然由专家的学历职称等因素确定专家的权重太过主观，但是这些因素在评价过程中仍然可以被考虑进去，在未来的研究中可以同时考虑主观权重与客观权重，并对两种权重进行融合得到最终的权重。