基于经验模态条件生成对抗网络的短期负荷预测

黄海荣，吴 君，郁 丹，苏本庆

(1.浙江华云电力工程设计咨询有限公司，浙江 杭州 310000；2.上海电力大学电气工程学院，上海 200090)

0 引言

电力系统短期负荷预测可以根据历史负荷变化情况，结合气象、经济等因素，估算未来某天的负荷需求[1]。准确的电力负荷预测是保证新型电力系统安全、经济运行的基础。因此，有必要研究电力负荷预测的新方法，以提高负荷预测的准确度。

目前，短期电力负荷预测模型一般分为时间序列模型和深度学习模型两类。其中，时间序列模型的代表主要有回归分析法、傅里叶展开法、卡尔曼滤波及自回归积分滑动平均模型等[2]。以上模型大多以线性模型为基础，考虑了数据间的时序性关系，但对非线性数据的预测能力较弱。随着近年来深度学习技术的兴起，基于深度学习模型进行短期负荷预测已成为相关领域的研究热点之一。如循环神经网络、卷积神经网络(convolutional neural network,CNN)、生成对抗网络(generative adversarial network,GAN)已应用于负荷预测并取得一定成果[3]。文献[4]建立了基于长短期记忆(long short-term memory,LSTM)网络神经和轻梯度提升机的组合预测模型，进一步提升了负荷预测的精度。文献[5]分别研究了LSTM神经网络、门循环单元神经网络和栈式自编码器应用于电力负荷预测时的效果。

为了进一步提高短期负荷预测的精度，研究人员常将原始信号进行分解，期望能够学习到原始信号在某些域中存在的特征。这些域包括时域、频域和其他变换域等[6]。基于此共识，研究人员多采用小波包、变分模态分解、经验模态分解(empirical mode decomposition,EMD)等算法，将历史负荷分解为不同的分量，再结合机器学习方法等进行预测，将各分量的预测值进行组合以得到预测结果。文献[7]提出了1种基于EMD和LSTM的短期电力负荷预测模型，提升了模型的非线性拟合能力和时间记忆能力。文献[8]提出了1种结合变分模态分解、注意力机制和改进的深度双向门控循环单元的短期负荷预测模型，提升了负荷预测的速度和精度。

条件生成对抗网络(conditional generative adversarial network，CGAN)能够捕捉非线性时间序列数据间隐含的深层关系，并且能考虑到气候、日期等因素的影响[9]。本文将EMD与CGAN相结合，建立了基于经验模态分解-条件生成对抗网络(empirical mode decomposition to conditional generative adversarial network,EMD-CGAN)的负荷预测模型。以实际算例对其进行验证，并与其他基于深度学习的负荷预测模型进行对比。对比结果表明，本文所提模型具有更小的预测误差。

1 基于EMD-CGAN的短期负荷预测原理

1.1 CGAN原理

GAN是1种通过对抗过程来估计生成模型的深度学习方法，包括生成器和判别器2个部分。其中，生成器可以学习真实数据的分布，将输入的随机噪声转化为判别器无法分辨的假样本数据；判别器可以区分输入数据是否为生成样本。两者通过相互博弈使GAN模型充分学习数据间隐含的深层关系并达到平衡。平衡后，理论上模型所生成的数据与真实数据相差无几。CGAN是对原始GAN的改进。CGAN保留了GAN生成器和判别器的博弈结构，并在此基础上增加了条件值y作为输入。随机噪声z与条件值y一起作为生成器的输入，通过生成器生成样本G(z|y)。判别器D则要判断对应条件下的生成样本是否与真实样本x相似，并将判别结果D(x|y)通过损失函数反馈给生成器和判别器。生成器和判别器根据反馈的损失函数更新自身参数并进行优化，从而达到纳什均衡。

CGAN结构如图1所示。

CGAN模型中判别器和生成器的损失函数如式(1)、式(2)所示。

LG=-Ez～Pz{D[G(z|y)|y]}

(1)

式中：D(·)为判别器输出的数据；G(·)为生成器输出的数据；E(·)为对应分布的期望值；z～Pz为噪声数据z的分布。

LD=-Ex～Px[D(x|y)]+Ez～Pz{D[G(z|y)|y]}

(2)

式中：x～Px为真实样本x的分布。

将LG、LD的损失函数进行组合，可以得到CGAN的目标函数，如式(3)所示。其训练目标为带有条件的2人极小极大值博弈。

Ez-Pz{log{1-D[G(z|y)|y]}}

(3)

当生成器完全学习到真实数据中隐含的深层关系时，LG、LD的损失函数可以得到最优解。

1.2 EMD原理

EMD是1种处理非线性非平稳信号的时频分析方法[10]。该方法可以根据负荷数据本身的时间尺度特性按频率由高到低将其分解为多个本征模态函数(intrinsic mode function，IMF)分量和1个残差(residual，RES)分量。每个IMF代表不同时间尺度下的负荷特征分量如式(4)所示。

(4)

式中：Pi(t)为多个IMF分量；Rn(t)为RES分量。

所有IMF必须满足以下2个条件：函数极值点的个数必须等于零点的个数或者相差个数等于1；对于任意采样点，由局部最大值点和局部最小值点组成的上下包络线的平均值为零[11]。

运用EMD对负荷进行分解的具体步骤如下。

①找出原始负荷数据的所有极大值点和极小值点。

②采用三次样条插值法，分别求得极大值点形成的上包络线e+(t)和极小值点形成的下包络线e-(t)。

③计算均值包络线e(t)。

(5)

④采用原始负荷数据P(t)减去均值包络线e(t)，得到新的负荷时间序列F1(t)。

F1(t)=P(t)-e(t)

(6)

⑤判断F1(t)是否满足IMF分量的2个条件。若不满足，则返回步骤①继续循环；若满足，则得到输入负荷数据的一阶IMF分量P1(t)。

⑥将原始负荷时间序列减去一阶IMF分量得到一阶残差分量R1(t)，并以其作为输入信号求得二阶IMF分量。

⑦重复上述过程，直至n阶残差分量Rn(t)的幅值小于预设阈值， EMD结束。

EMD分解可以将原始负荷时间序列分解为多个时间尺度下的负荷特征分量和一个残差分量，从而提高负荷预测的精度。

2 基于EMD-CGAN的负荷预测模型

2.1 EMD-CGAN结构

EMD-CGAN结构如图2所示。

为了解决原始GAN对负荷进行短期预测时存在的预测精度不高、模型不稳定等问题，本文结合EMD与CGAN，提出了基于EMD-CGAN的负荷预测模型。

EMD-CGAN主要包括EMD、生成器和判别器3部分。由图2可知，EMD-CGAN的生成器由n个LSTM组成。LSTM 具有较好的记忆性能，并且在短期负荷预测中表现良好，所以在生成器中采用n个LSTM网络分别对n个负荷特征分量进行预测，再对其输出进行求和即可得到负荷预测值。

EMD-CGAN在CGAN的基础上将生成器的输入由随机噪声改为历史负荷数据，并增加了1个EMD模块将历史负荷数据分解为多个经验模态分量和1个残差分量，使得生成器可以学习到多个时间尺度下的负荷特征。这不仅降低了生成模型的复杂度，还可以提高负荷预测的精度。

模型的网络参数及意义如表1所示。

表1 网络参数及意义

判别器的作用是判别输入数据是生成数据还是真实数据，相当于1个二分类器。由于CNN具有较好的特征提取能力，且在分类任务中表现良好，所以判别器采用CNN。判别器结构如图3所示。

判别器由多个卷积层和1个全连接层组成。负荷预测值和实际负荷值分别与条件值拼接成1个矩阵作为判别器的输入，经过多层卷积后提取到高维数据的低维特征，并通过全连接层得到判别信息。

2.2 基于EMD-CGAN的负荷预测流程

EMD-CGAN构建后，首先将历史数据分为训练集和测试集(训练集数据和测试集数据不重叠)，然后采用训练集数据对模型进行训练，最后运用测试集数据对已训练负荷预测模型进行验证。

EMD-CGAN模型的预测过程如下。

①数据预处理。考虑到历史负荷数据和负荷影响因素具有不同的量纲和量纲单位，且试验数据分布区间跨度较大，会影响深度学习模型在进行梯度下降求解时的下降速度，因此对试验数据采用归一化操作。归一化表达式为:

(7)

式中：X为要归一化的数据；Xt为归一化后的数据；Xmin为原始数据的最小值；Xmax为原始数据的最大值。

②EMD-CGAN模型的优化训练。首先，对经过预处理的历史负荷数据x进行EMD，得到(n-1)个本征模态函数和1个余波。然后，将这n组数据分别与条件值y进行拼接输入到生成器的n个LSTM神经网络中，并对n个LSTM的输出求和得到负荷预测数据。最后，将负荷预测数据、真实数据分别和条件值一起输入判别器，将真实数据的判别结果和预测数据的判别结果组成交叉熵反馈给判别器和生成器，从而对模型进行优化训练。

③负荷预测。首先，将历史负荷数据和条件值输入已训练的EMD-GAN网络后，生成器输出负荷预测值。然后，对负荷预测值进行反归一化，即可得到负荷预测结果。

2.3 评价指标

目前，负荷预测结果的评价指标主要有均方根误差(root mean square error，RMSE)和平均绝对百分误差(mean absolute percentage error，MAPE)。其中：RMSE反映了负荷预测的准确度；MAPE反映了预测模型的拟合度[12]。两种指标的表达式如式(8)和式(9)所示。

(8)

式中：x′i为预测负荷值；xi为实际负荷值；m为样本数量；R为RMSE。

(9)

式中：M为MAPE。

3 算例分析

为验证预测模型的准确性，本文选取中国浙江某地配电网2016—2017年的电力负荷数据以及气象数据(温度、湿度、风速)作为试验数据集，对所提短期负荷预测方法进行验证。其中，负荷数据和气象数据的时间分辨率均为15 min，即每日各类数据均有96个采样点。选取前70%历史数据作为训练集、其余历史数据作为测试集，并以前1周的历史负荷数据和气象数据作为输入预测未来24 h的负荷。

3.1 EMD负荷序列

本文对历史负荷数据进行EMD。对于不同的历史负荷数据，分解得到的IMF项数可能是不同的。为保证生成器输入的IMF项数相同，本文对不同负荷数据进行多次EMD。经过试验发现，IMF的前6项已经能很好地描述历史负荷周期性趋势。因此，本文将所有试验的IMF都设为6项，将余项纳入RES项进行处理。浙江某地区1周负荷数据EMD结果如图4所示。

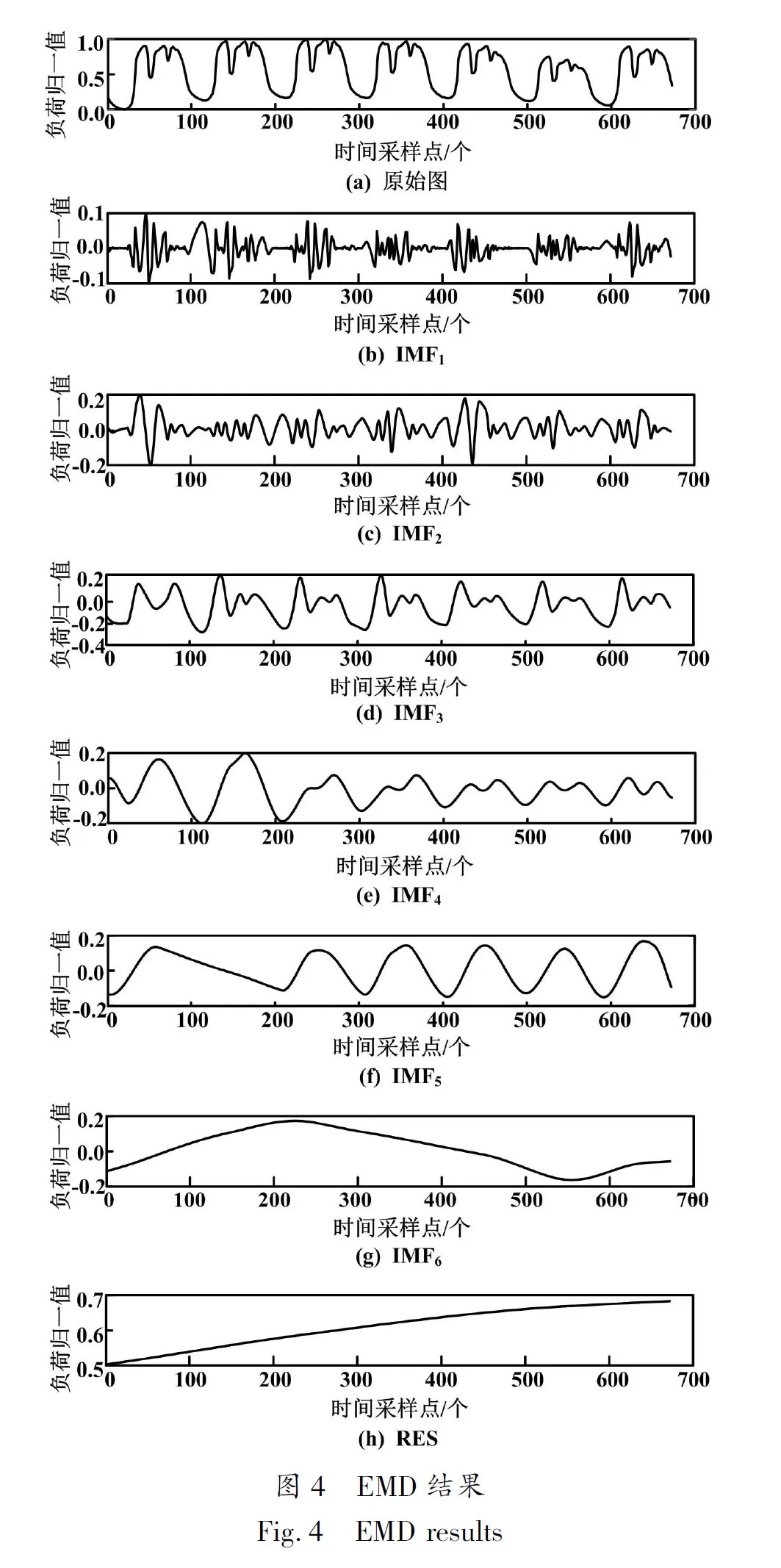
由图4可知，经过 EMD 算法分解后的各IMF分量的规律性强于原始负荷，更有利于LSTM神经网络对电力负荷数据特征的学习。

3.2 EMD-CGAN预测结果与对比分析

本文建立的EMD-CGAN的生成器由7个 LSTM 神经网络构成。每个LSTM神经网络由2个隐藏层和1个输出层组成。隐藏层的神经元个数为20。激活函数为tanh，学习率为0.001。判别器则由3层CNN和1个全连接层构成。其中：3层CNN的卷积核大小均为5×5；卷积核个数分别为32、64、128；滑动步长均为2；激活函数为LReLU；学习率为0.001；池化方法为最大池化。

本文采用训练集数据对EMD-CGAN模型进行训练。模型训练完成后，运用测试集数据验证模型的有效性。EMD-CGAN预测结果如图5所示。

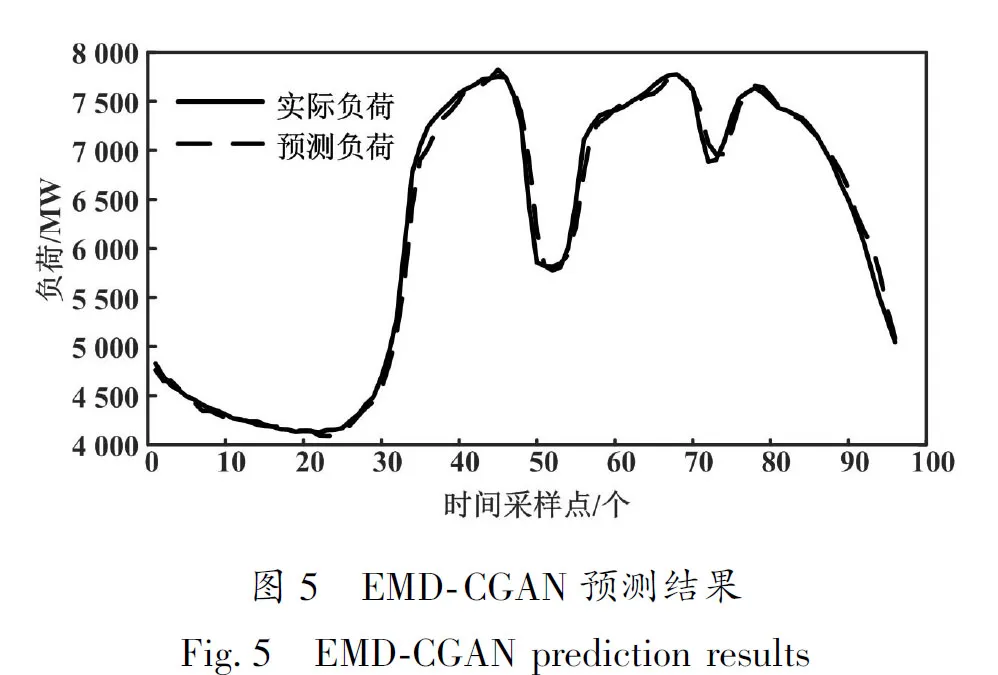
由图5可知，预测负荷和实际负荷基本吻合。

为了进一步验证本文模型的有效性，在同等条件下，将本文所提方法预测结果与LSTM、EMD-LSTM以及CGAN的预测结果进行对比。不同算法负荷预测结果如图6所示。

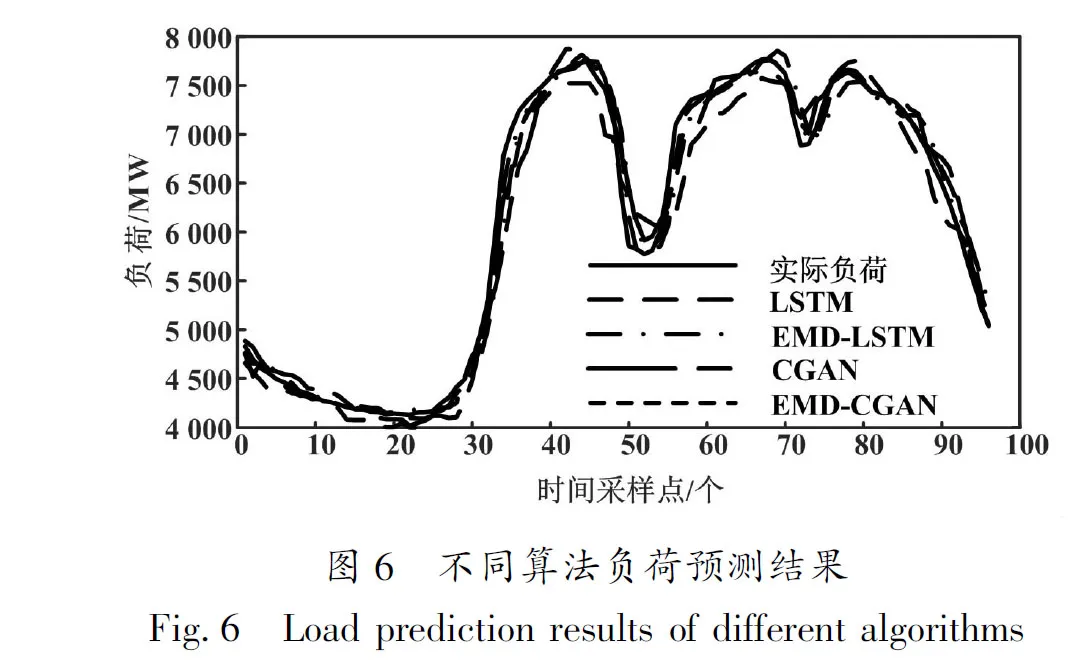
对4种负荷预测方法预测结果的RMSE 值和MAPE值进行计算。各方法预测误差对比如表2 所示。从RMSE角度来看，本文所提方法与 LSTM、EMD-LSTM、CGAN相比，RMSE分别下降了120.893 MW、80.287 MW、99.253 MW。从MAPE角度来看，本文所提方法相对于其他算法的MAPE分别下降了1.646%、0.876%、1.189%。综上所述，本文所提出的基于EMD-CGAN的短期负荷预测方法相对于其他方法具有更小的预测误差。

表2 各方法预测误差对比

4 结论

针对复杂环境下历史负荷数据呈现随机性、非线性的特点，本文提出1种基于EMD-CGAN 的短期负荷预测模型。该模型充分考虑了负荷数据本身的时间尺度特征以及外部环境因素的影响，提高了基于深度学习短期负荷预测模型的效率和精度。然而，本文所建模型在实际预测中并未分析各负荷影响因素与不同IMF分量之间的关联关系，而是直接将所有条件值与IMF分量进行组合。后续研究可以考虑不同负荷影响因素对各IMF分量预测精度的影响程度，针对不同的IMF分量选择不同的条件值进行拼接，从而进一步提升负荷预测效率和精度。