基于随机流网络模型的转向架系统可靠性评估
2022-12-23高昆仑李洪辉张胜涛
高昆仑 李洪辉 张胜涛
中车青岛四方机车车辆股份有限公司 山东 青岛 266111
引言
随着铁路系统结构和功能的不断完善,铁路系统的安全性和可靠性也愈加重要。轨道车辆转向架的可靠性直接影响着列车运行的安全性和稳定性。转向架作为轨道列车的一种典型、复杂的重要子部件,轻微的部件故障可能直接导致系统损坏。因此,转向架系统的可靠性分析是当前铁路客车设计、制造领域的一个重要课题。
现有的文献主要以转向架系统的二元性研究为主,但在实际情况下,转向架的所有部件都会随着时间的推移发生机能退化,直至完全丧失功能。因此,本文将转向架系统描述为一个作用于不同能力水平,以满足起止点间给定需求的随机流网络模型[1]。最后,提出了一种基于最小割集的组合可靠性评估方法。
1 基础理论
1.1 转向架系统
转向架系统组成根据转向架的类型和功能不同而相异,但其基本包括轮对、构架组成、一系悬挂、二系悬挂、缓冲挡、抗蛇行减振器、垂向减振器、横向减振器、制动系统等,如图1所示。
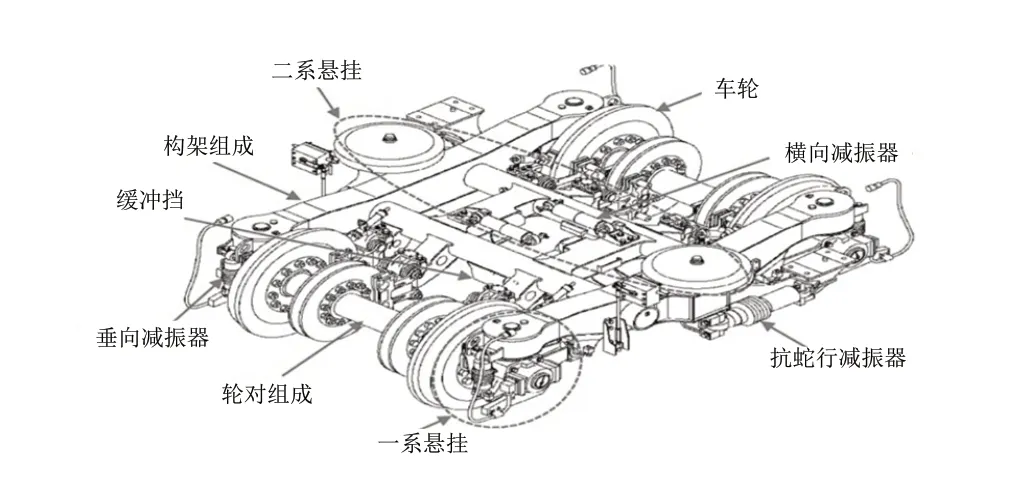
图1 某型转向架组成示意图
本文主要研究上述转向架机械部件之间的力传递问题,将施加在这些组件上的具有方向和大小的作用力看作一种网络流,且随着时间的推移而变化,因此网络流被看作为随机变量。本文将转向架部件之间的力传递视为一个随机网络流,并对给定需求的起止点间的可靠性进行评估。
1.2 随机流网络模型
随机流网络可定义为有向图G(V,E,C),其中V为顶点集,E为边的集合,C为能力状态的集合,如图2所示。
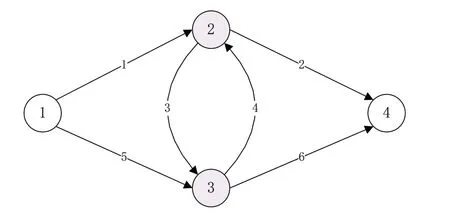
图2 一个4N6L的随机流网络
在随机网络中,每条链路都有多个独立的能力状态,范围从0到n,且具有不同的概率分布。如果链路a1处于能力状态0,则认为该零部件处于完全故障状态;如果链路a1处于能力状态n,则认为该零部件正常运作。随机网络的节点对可靠性可以用该起止节点对能够传递的最大流量不小于给定需求d的概率来计算,即随机网络能够将需求d从源节点传输到目的节点的概率。
2 求解方法
2.1 随机流网络建模
转向架除了支撑车体作用外,还具有传递牵引力、吸收曲线轨道振动、控制制动力等功能[2]。施加在转向架各部件上的作用力的方向和大小,代表转向架系统中的网络流。根据文献[3],转向架部件传递的作用力可以分为三种类型:①垂向力,车体对二系橡胶弹簧施加的垂直力作用于转向架构架,转向架构架从而对轴箱弹簧产生压力,并传递至轴箱组成,表现为车轮的垂直振动。②纵向力,与垂向力的方向相反。③横向力,由离心力和列车在弯曲的轨道上高速运行时产生的力引起。
利用作用力的传递路径和方向,将转向架系统的网络结构形象化,如图3和图4所示。

图3 转向架系统的受力情况
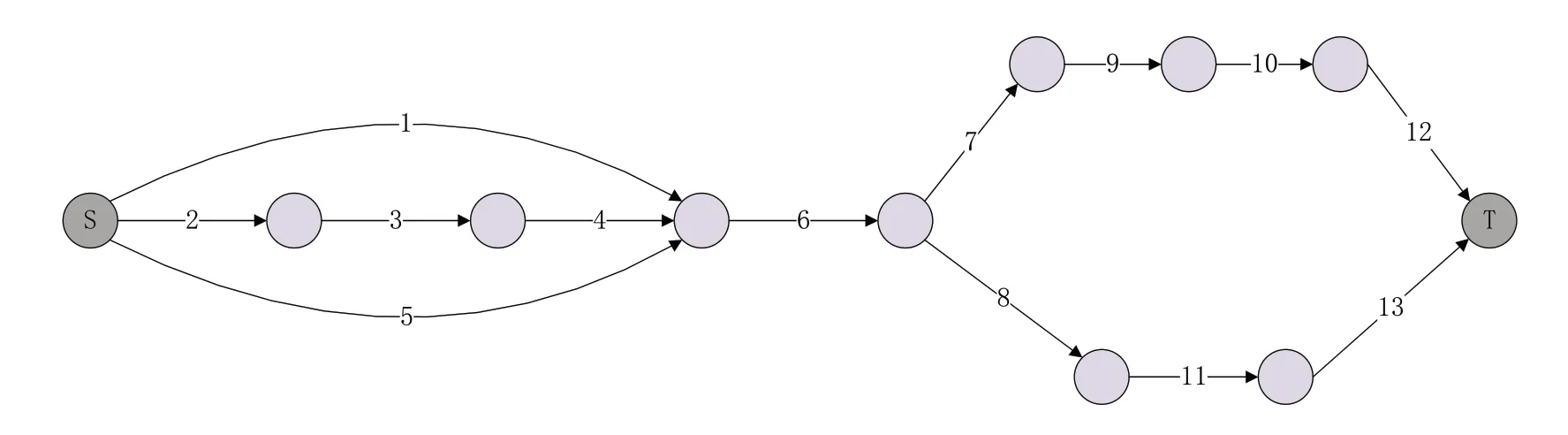
图4 转向架系统网络模型
在图4中,网络的边表示转向架的机械组件,顶点表示组件之间的力传递路径。虚线表示在垂直力方向上支撑车轮的轨道车辆。本文考虑零部件机械功能的劣化水平,表1为转向架各部件的劣化能力状态及其概率分布。
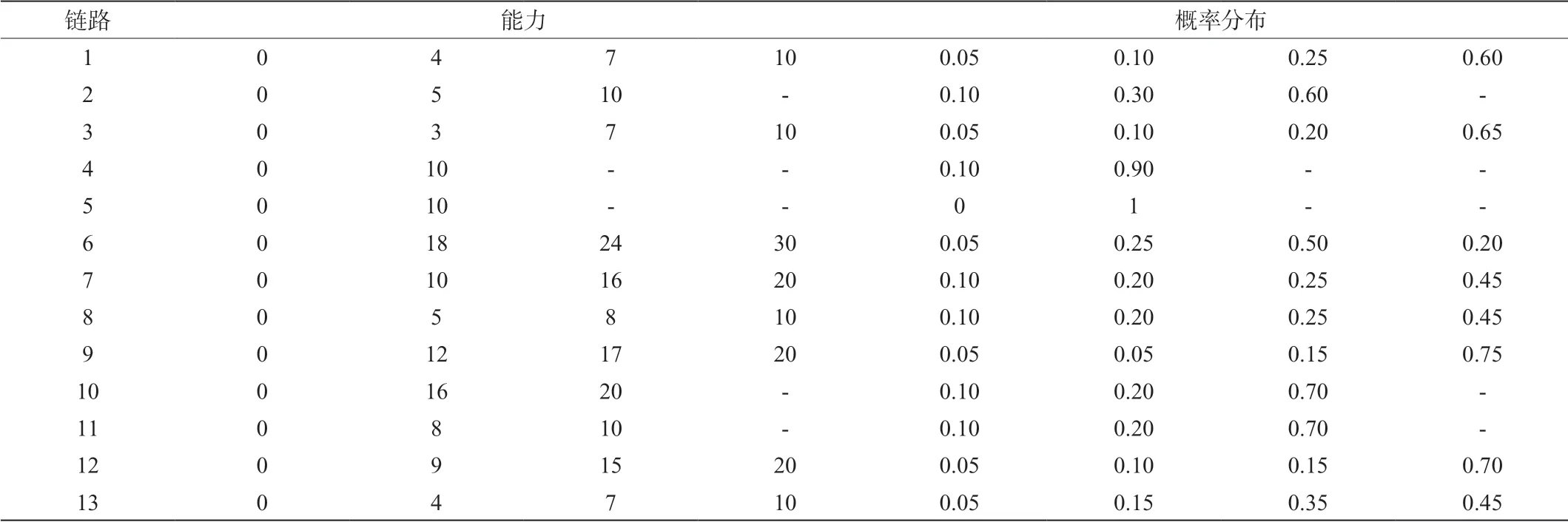
表1 转向架各部件能力概率分布数据
为了评估转向架系统的随机流网络可靠性,提出以下假设条件:①节点是静态独立和完全可靠的,即转向架各组件之间的连接总处于运作状态。②网络中的流量满足流量守恒定律。③由于转向架各部件间的作用力具有特定的方向,随机流网络视为有向网络。④每个部件的机械能力是一个非负整数,且服从一定的概率分布。
2.2 求解步骤
2.2.1 获取最小割集。第一步,采用文献[3]提出的方法生成最小割集。首先确定节点割集,节点割集是相互直接连接的节点集,移除节点后,剩余的随机网络将分为两部分。由于实际网络中节点数量比链路数量少,因此,通过计算节点割集的方式比寻找链路割集的效率更高。每个节点集都有两个特定的参数,分别用nHigh和nMax两个符号表示。其中,nHigh表示该节点集的最大节点数,nMax表示与该节点集的节点连接的最大节点数。例如,图2中的随机流网络,对于节点集{2},nHigh为2,nMax为3;对于节点集{3},nHigh为3,nMax为3。
对于高阶生成的节点集,包括从nHigh+1到nMax的其余节点号,继续该过程直至(n-1)生成。例如,图2中的随机流网络,对于一阶节点集{1},下一阶可能的节点集是{1,2},{1,3}。对于二阶节点集{1,2},下一阶节点集是{1,2,3}。
然后,通过对链路集进行集合论X上二元关系R的传递运算,将得到的节点割集转换为链路割集。因此,图4的网络结构通过应用上述方法获得的转向架系统最小割集如表2所示。

表2 图4所示网络的最小割集
2.2.2 获取无冗余最小割集。搜索割集中存在的每个链路,并与新增的链路进行组合。如果网络中存在的所有链路都包含在内,剩余的最小割就无法生成新的组合。因此,剩余的割集被视为冗余割集。例如,表2中的割集11中没有之前未考虑过的链路,不能从这个割集中生成新的组合。因此,割集11是一个冗余割集。消除冗余最小割集将有助于减少算法运行时间以快速评估转向架系统的可靠性。表3给出了获得的无冗余最小割集。

表3 图4所示网络的无冗余最小割集
2.2.3 可靠性计算。使用获得的最小割集对转向架系统进行可靠性评估,将逐个搜索每个割集,以评估该割集的不可靠性。此过程将从形成第一个割集中存在的所有可能的能力组合开始,将每个组合的能力相加,并计算每个组合的概率值。选择总能力小于给定需求d的组合,将这些组合的概率相加。由此产生的概率将表示该特定割集的不可靠性。将剩余的组合存储在数组残余组合中,这些组合是能够传递需求d的链路。
例如,表3中第5个割集{7,8},假设通过网络传递的需求量为30个单位,则可能的割集组合为[(0,0),(0,5),(0,8),(0,10),(10,0),(10,5),(10,8),(10,10),(16,0),(16,5),(16,8),(16,10),(20,0),(20,5),(20,8),(20,10)]。每种组合的概率分别为[0.01,0.02,0.025,0.045,…,0.09,0.1125]。筛选总能力小于给定需求量为30个单位的组合,分别为[(0,0),(0,5),(0,8),(0,10),(10,0),(10,5),(10,8),(10,10),(16,0),(16,5),(16,8),(1610),(16,10),(16,10),(16,10),(16,10),(16,10),(16,10),(16,10),(16,10),(16,10),(16,10),(16,10),(1610),(16,10),(1610),(20,0),(20,5),(20,8)]。其中,组合(20,10)的传递能力等于需求量,因此不包含该组合,将其存储在数组残余组合中。将所有被选择组合的概率相加,得到第5个割集{7,8}的不可靠性,即{7,8}割集失效而导致网络失效的概率。
重复该过程,直到所有割集的不可靠性计算完成。最后,对于给定的需求d,通过公式“网络可靠性=1-网络不可靠性”,将不可靠性值转换为可靠性表达式。
在各种需求量情况下,图4所示的转向架系统的可靠性如表4所示,其中R是转向架在给定需求量d下保持稳定运行的可靠性。

表4 不同需求量d情况下转向架系统可靠性
3 结果分析
通过第2节描述的求解算法,得到如表5所示的不同需求量情况下转向架系统随机流网络可靠性结果,它代表了转向架在特定环境下处于正常运行状态的概率。例如,当需求量d=20,R=0.27929399时,这意味着如果我们在以表1中给出的条件为前提,且起止点间最小适用力是20个单位,那么转向架处于正常运行状态的概率是0.27929399。
4 结束语
本文提出了一种考虑转向架系统各机械部件劣化能力的轨道列车转向架系统随机流网络可靠性评估方法。首先,在分析转向架各部位受力情况的基础上,根据受力方向和大小建立了网络模型。考虑转向架各部件的机能劣化,本文将各部件的运行状态描述为随机流网络。然后,提出了一种基于最小割集的转向架系统可靠性评估方法,该方法可用于轨道车辆转向架系统可靠性分析和运行维护分析,后续可从转向架系统的实际应用角度出发进行研究,以提高和改进研究方法的实用性。
