多自由度机器人位姿稳定性控制方法研究

刘媛

多自由度机器人位姿稳定性控制方法研究

刘媛

（安徽电子信息职业技术学院 机电工程学院，安徽 蚌埠 233000）

对于多自由度机器人位姿控制方法来说，机器人位姿稳定性受到各种因素的干扰，容易发生位姿失稳现象，为此，提出一种新的方法来解决此问题。采用扩展卡尔曼滤波算法实现多自由度机器人各个传感器数据的有效融合，获取多方位机器人位姿数据；通过传感器信号处理去除机器人位姿测量噪声，使用自适应扩展技术实现机器人参量与姿态角校正信息融合，通过反演积分项自适应调节姿态参量并弥补稳态误差，实现机器人的位姿稳定控制。仿真实验结果表明，该控制方法能够准确实现多自由度机器人位姿稳定性控制，即使引入扰动机制仍然不会出现控制失衡，具有较好的稳态控制效果。

多自由度；机器人；位姿稳定性；扩展卡尔曼；滤波算法；反演积分项

从机器人第一次诞生以来，人类对于机器人的设计热情一直有增无减，目前机器人技术广泛应用于医疗领域、娱乐领域以及服务领域，为人类生活提供便利的同时也为科学研究提供新的方向[1]。目前最常使用的工业机器人主要为多自由度机器人或者多关节机器手臂，机构包括底座、臂部、腕部以及手部等，由于结构之间常常使用串联，因此也被称作是串联机器人[2]。多自由度机器人并不是只能作为一种代替劳动力的设备，而是一种多感知的智能体。多自由度机器人可以像人类一样对周围环境开展分析判断并作出对应的反应，同时还能够具有较高的精密性和超强续航能力，即使在恶劣的工作环境中仍然能够高效完成工作任务。经过近60年的技术变革，多自由度机器人的发展过程涵盖三个阶段：①学习型机器人：这类机器人需要人类操作或者通过模仿学习才能按照既定程序完成工作内容，机器人通过模仿学习将工作任务写入程序之中，这类机器人适应周围环境的能力较差[3]；②感知机器人：这类机器人由于添加传感装置，具有视觉或者听觉能力，根据周围环境对自身的工作状态做出调整，工作效率较高[4]；③智能机器人：这类机器人是近年重大科学研究成果，机器人不但能够感知周围环境，还能具有自己的判断能力，决策能力与推理能力都较高，面对复杂工作也能完美解决，因此近年来在高精尖科学领域以及军事领域广泛使用[5]。

机器人的研制与发展不断进步，因此对于多自由度机器人的位姿控制相关研究的要求也逐渐提高，比如使用多角度机器人实行喷涂或者焊接这类控制要求较高的工作时，对于多自由度机器人的位姿控制要求较高，才能符合工作环境的要求[6-8]。以喷涂机器人为例，开展喷涂工作时要求多角度机器人末端具有高度稳定姿态，这就要求多自由度机器人至少具备6个关节结构才能满足喷枪空间姿态与位置姿态的合理要求。国外在机器人研究领域起步较早，早在上世纪美国众多公司已经将多种类型的机器人应用在机器建造行业以及服务行业[9]；日本也在餐饮、娱乐、家庭中广泛使用多自由度机器人[10]。除了工业、服务业领域以外，国外许多公司都致力于研究多自由度机器人在军事领域的可行性，并且美国及欧洲诸国都已经将几十种不同功能及形态的机器人装备在军队武装之中。我国机器人控制相关研究起步较晚，但是近年已经取得可观成绩。马芳武等提出一种轮腿式全地形移动机器人位姿闭环控制方法[11]，针对轮腿机器人的位姿问题分别建立俯仰和侧倾模型，并对轮腿机器人的位姿进行解耦运算，通过解耦计算得到机器人的质心位置，进一步实现机器人位姿控制实现其姿态的闭环控制。利用Simulink与Adams联合仿真验证轮腿机器人在立体坡面上的位姿控制效果，此方法能够提升位姿控制效果，但是任然存在位姿失稳现象。王杰鹏等提出力觉交互控制的机械臂精密位姿控制方法[12]，在机器人末端安装力矩传感器，获取机器人末端负载重力和末端所受外部作用力，通过传感器获得机器人的状态，计算外部作用力，实现外部作用力对机械臂末端位姿的精密控制。此方法计算量小，计算速度快，但是机器人位姿稳定性控制效果不佳。

针对以上问题，本文研究多自由度机器人位姿稳定性控制方法，探索更加高效可控的机器人位姿控制方法。

1 多自由度机器人位姿获取

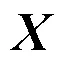
式(3)为机器人姿态的状态预测方程：

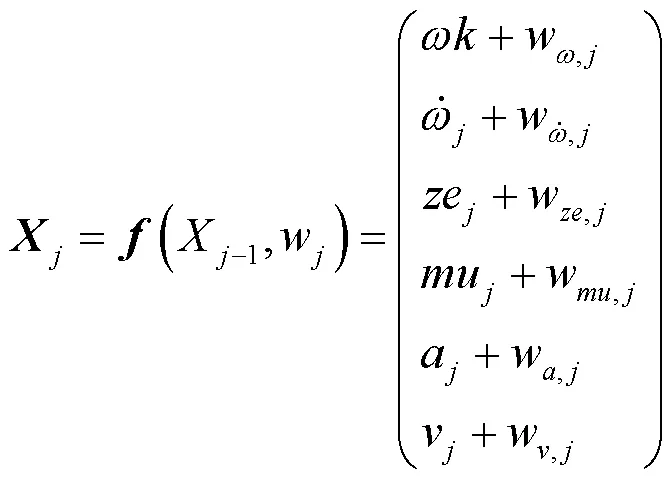
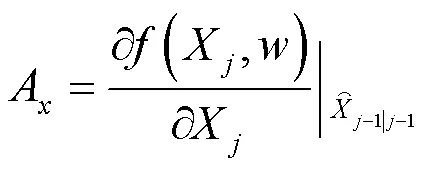
式(6)为用于测量机器人姿态的方程：

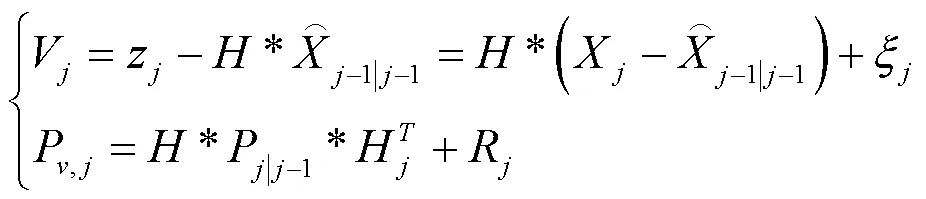
由此得到自适应扩展科尔曼滤波算法的全部形式：

根据以上算法完成机器人传感器信号处理，同时获得机器人的当前位姿：

2 位姿稳定性控制方法

经过上文研究获得多自由度机器人位姿数据，以此为基础开展多角度机器人稳定性控制律设计，实现机器人位姿稳定性控制。使用反演稳态误差补偿稳定性位姿控制律，仍旧使用扩展卡尔曼滤波算法校正机器人姿态角并融合参量[14]，扩展卡尔曼滤波算法传递函数如式(12)所示：

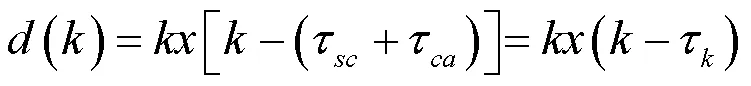
假设原始状态使用0表示机器人位姿向量，此时稳态误差出现。通过反演积分项弥补稳态误差，依据可能出现的结果修正姿态参量，把反演积分导入自由度运动规划空间中，获得控制机器人姿态稳定性的Lyapunov函数：

依据Lyapunov稳定性原理，获知控制机器人的方法实际上是一个反演闭环控制方法。Lyapunov泛函数矩阵需要大于0，证明对于多自由度机器人的控制实现稳态渐近收敛。

3 仿真实验结果

为验证本文方法的实际应用性能，在模拟实验平台中开展多自由度机器人模拟实验，参与实验的多自由度机器人型号为LBR iiwa7轴自由度机器人（7个机器关节），实验过程主要测试机器人行进过程以及物体抓取过程中的位姿稳定控制效果[15]。

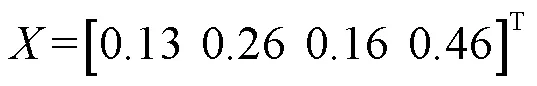
统计机器人在抓取物体时姿态角产生的误差，统计结果见图1。

图1 角度偏差实验数据曲线图

通常情况下，控制结果与真值之间的误差越小，说明控制效果越好。从图1中能够看出，使用本文方法对研究七轴多自由度机器人的位姿实行定位控制时，控制结果与真值之间的误差较小，说明使用本文方法控制多自由度机器人能够获得更加平滑的控制效果，且控制过程中没有产生明显的零点漂移，也就是说使用本文方法控制多自由度机器人时能够获得良好的控制效果。

为实现控制效果对比，分别使用以多连杆悬挂方法作为基础的机器人位姿控制方法以及力学交互作为基础的机器人位姿控制方法开展对比实验，对于各关节的控制性能见表1。

从表1中能够看出多连杆悬挂法控制多自由度机器人时需要较长时间才能到达目标位置，同时控制到达目标位置的速度由初始与目标位置之间的差值决定，差值越大，到达目标位置越慢，只有低速运行才能得到高稳态精度与低超调量，如果把每个关节的目标位置做出适当更改，需要重新计算恰当参数并将运动区间重新划分，所以使用该方法控制机器人位姿时，过程更加复杂。力学交互法控制多自由度机器人各个关节时，能够在一定程度上改善机器人每个关节到达目标位置的时间，提高控制机器人的精度，但是使用这种控制方法在一定程度上增加了各个关节在工作过程中的超调量。由此能够看出，使用该方法控制多自由度机器人需要先将机器人自身的动态特性忽略，以此提高控制机器人的稳态精度同时缩短控制时间，但是这样却是舍本逐末，在实际工作时不被允许使用。从表中可以直观地看出本文方法控制多自由度机器人时，实现关节运动所花费的时间最少，而且使用本文方法没有出现超调控制，这一结果与图1中的结果接近。对比3种方法对于多自由度机器人的控制结果，从稳态精度的角度分析控制效果，使用本文方法控制多自由度机器人稳态精度较高，由此可以证明，使用本文方法控制多自由度机器人经过具有较高的精度的协调控制结果。

表1 多自由机器人关节控制性能对比

对多自由度机器人添加扰动条件，分析存在干扰的情况下，分别使用3种方法再次对多自由度机器人实行控制。仿真实验时，不能记录机器人程序中的时间变量，所以加入扰动时需要分析机器人程序的循环次数，加入扰动之前先要保证机器人程序处于稳定状态之下。在控制输出过程中加入扰动，扰动幅值为6，每600个程序循环周期内持续扰动。以处于中间位置的关节编号4为该部分仿真实验的主要数值统计对象，在实验开始的第30s加入扰动，数据统计内容为抓取偏转角，3种方法的控制情况见图2。

图2 扰动状态下多角度机器人位姿控制曲线

从图2中能够看出，使用多连杆悬挂法控制多自由度机器人时，受到扰动，机器人关节出现短暂变化，这种扰动造成机器人关节在一定程度上从原有的平衡状态中偏离，最大变化幅度约为9º，但是使用该方法控制多自由度机器人，能够使关节在10s内重新恢复到原来位置，由此可以看出多连杆悬挂法存在一定鲁棒性。发生扰动时使用力学交互法控制多自由度机器人出现控制输出饱和情况，这种饱和情况能够帮助机器人尽快恢复到原有的平衡状态，但是使用该方法控制机器人时出现对扰动极高敏感情况，机器人关节位置出现极大变化，尽管该控制方法已经尽量快速做出速率调节，但是位置偏移仍旧较大，不能快速调节机器人关节恢复平衡状态，此时需要机器人自身牺牲较大能量才能实现速率快速调节，但是这种情况不被实际工作允许。在图2中能够看出，使用力学交互控制法大概需要30s才能使机器人关节回到原有位置，这也看出该方法不具备较高的鲁棒性。从图2中能够明显看出，使用本文方法控制多自由度机器人时只出现极为微小的位置偏移，这种偏移几乎没有被察觉出来，说明使用本文控制方法，在受到扰动干扰后使用本文方法继续控制多角度机器人，位姿并不会出现失衡状态，由此说明本文方法控制效果较好且具有较高鲁棒性。

4 结论

多自由度机器人正常、高效工作的前提是先保证具有准确且稳定的位姿情况，因此，本文研究多自由度机器人位姿稳定性控制方法，探索该机器人的位姿稳定控制。通过自适应卡尔曼滤波算法与反演积分项，融合机器人参量并补偿位姿误差，实现机器人的有效稳定控制。通过模拟环境的仿真实验发现，本文的控制方法与真实控制效果具有较高拟合度，即使引入扰动机制，仍然比同类方法的控制效果更稳定。尽管本文研究只针对多自由度机器人，但是未来经过反复仿真实验与调整必然具有广阔的应用前景。

[1] 甄冒发，徐振峰，谢宇. 多自由度机器人惯性误差反馈融合闭环控制[J]. 微电子学与计算机，2020, 37(12): 77-80.

[2] 王琳玮，邵星灵，杨卫. 基于惯性传感器的球形机器人位姿控制系统及实验研究[J]. 中国测试，2020, 46(03): 123-127.

[3] 唐翠微. 基于多目标优化克隆算法的机器人模糊控制研究[J]. 机床与液压，2020, 48(21): 51-56.

[4] 李小彭，尚东阳，李凡杰，等. 输电线巡检机器人位姿变化的柔性关节控制策略[J]. 东北大学学报（自然科学版），2020, 41(11): 1577-1583.

[5] 张千，高国琴. 并联机器人串类水果抓取模型及抓取位姿计算[J]. 农业工程学报，2019, 35(23): 37-47

[6] 王君，徐晓凤，董明利，等. 单目移动机器人相对位姿估计方法[J]. 应用光学，2019, 40(04): 535-541.

[7] 刘飞飞，朱杨林，彭辉辉，等. 基于高增益观测器的单球移动机器人控制[J]. 控制工程，2020, 27(05): 799-806.

[8] 胥芳，丁信斌，占红武. 高精度移动目标位姿测量方法[J]. 高技术通讯，2019, 29(02): 119-133.

[9] 冯钧，孔建寿，王刚. 一种柔性空间双臂机器人的协同控制和避障方法[J]. 空间控制技术与应用，2020, 46(05): 10-17.

[10] 张蔚然，鲁守银，吴林彦，等. 基于模糊补偿的主从式上肢外骨骼康复机器人训练控制方法[J]. 机器人，2019, 41(01): 104-111.

[11] 马芳武，倪利伟，吴量，等. 轮腿式全地形移动机器人位姿闭环控制[J]. 吉林大学学报（工学版），2019, 49(06): 1745-1755.

[12] 王杰鹏，谢永权，宋涛，等. 力觉交互控制的机械臂精密位姿控制技术[J]. 机械设计与研究，2019, 35(04): 47-52.

[13] 樊绍巍，吴军，金明河，等. 同步三指式末端执行器的目标位姿估计方法[J]. 哈尔滨工程大学学报，2019, 40(02): 359-364.

[14] 赵德超，彭力，王皓. 非完整机器人目标跟踪控制器的设计与实现[J]. 计算机工程，2019, 45(01): 297-302.

[15] 唐宇存，李锦忠，林安迪，等. 基于三坐标测量机的机器人位姿精度检测方法[J]. 计算机工程与应用，2020, 56(05):257-262.

Research on pose and pose stability control of multi-dof robot

LIU Yuan

(School of Mechatronic Engineering, Anhui Vocational College of Electronics Information Technology, Anhui Bengbu 233000, China)

For the pose control method of multi degree of freedom robot, the pose stability of the robot is disturbed by various factors and prone to pose instability. Therefore, this paper proposes a new method to solve this problem. The extended Kalman filter algorithm is used to achieve the effective fusion of the sensor data of the multi DOF robot, and the pose data of the multi-directional robot is obtained. The sensor signal processing is used to remove the pose measurement noise of the robot. The adaptive extension technology is used to realize the information fusion of the robot parameters and the attitude angle correction. The inverse integral term is used to adaptively adjust the attitude parameters and compensate for the steady-state error, so as to realize the pose stability control of the robot. The experimental results show that the control method can accurately realize the pose stability control of the multi DOF robot, even if the disturbance mechanism is introduced, the control imbalance will not appear, and the control effect is good.

multi-dof；robot；pose stability；extended Kalman；filtering algorithm；inverse integral term

2021-09-02

安徽省教育厅质量工程项目——安徽电子信息职业技术学院蚌埠凯盛工程技术有限公司机电一体化示范实训中心（2019xqsxzx55）

刘媛（1982-），女，安徽蚌埠人，讲师，硕士，主要从事工业机器人、自动化应用研究，mnb998877@126.com。

TP242;TP273

A

1007-984X(2022)02-0032-06