齐齐哈尔地区不同人群对COVID-19疫情防控了解情况分析

张权，郑鹏晖，宇世航，关宝玲

齐齐哈尔地区不同人群对COVID-19疫情防控了解情况分析

张权，郑鹏晖，宇世航，关宝玲

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）

为了解新冠疫情流行期间齐齐哈尔地区不同人群获取新冠疫情防控知识的渠道，采用整群抽样的方法，对齐齐哈尔地区不同人群进行抽样调查，结果显示不同人群有着较大差异，为今后开展突发公共卫生以及新发传染病防控教育提供理论依据。

新冠疫情；防控；调查问卷

多元统计分析是一种综合分析方法，它能够在多个对象和多个指标互相关联的情况下分析它们的统计规律，其主要包括聚类分析、判别分析、主成分分析、因子分析、对应分析以及典型相关分析等方法[1]。本文选取对应分析的方法对齐齐哈尔市不同人群了解疫情防控知识的渠道展开研究，探索疫情冲击下不同群体了解疫情防控知识的渠道是否有差异，为今后开展突发公共卫生以及新发传染病防控教育提供针对性的理论依据[2-3]。

1 研究对象

对齐齐哈尔建华区、昂昂溪区、铁锋区三地居住的817名用户发放问卷，其中建华区287人（35.13%）、昂昂溪区246人（30.11%），铁锋区284人（34.76%)[4-5]。按性别分类，男性483人（59.11%），女性334人（40.89%）；按年龄分类，各年龄段具体问卷数如图1所示。

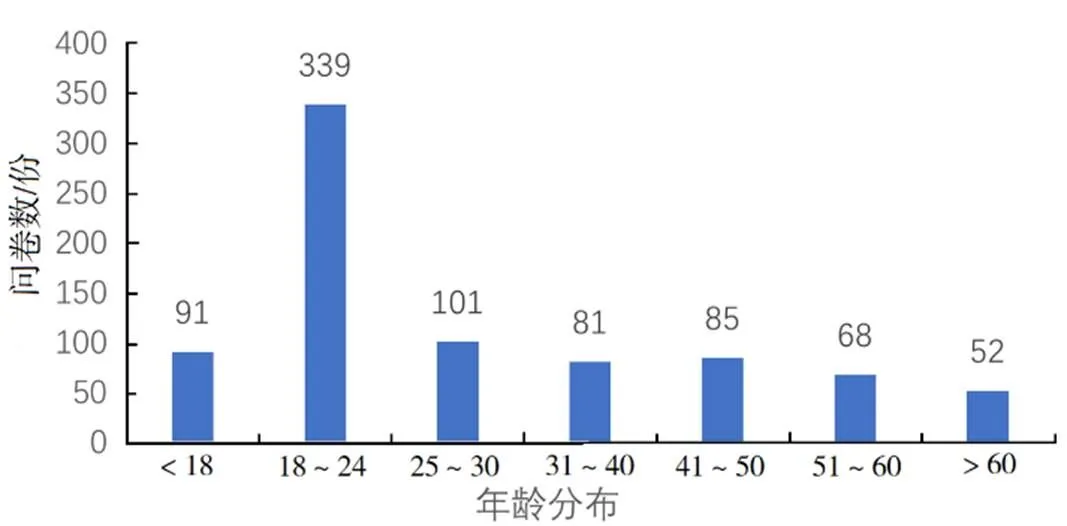
图1 年龄分布

2 对应分析

2.1 对应分析概念

对应分析的基本思想是将一个联列表的行和列中各元素的比例结构以点的形式在较低维的空间中表示出来。它最大特点是能把众多的变量同时作到同一张图解上，将其大类及其属性在图上直观而又明了地表示出来，具有直观性。另外，它还可以进行直观的分类，而且能够指示分类的主要参数（主因子）以及分类的依据，是一种直观、简单、方便的多元统计方法。本文选取了3个类别（区域、性别、年龄）与疫情防控渠道之间进行对应分析，能够很好地展现出不同类别对获取疫情防控知识渠道的影响以及联系。

2.2 不同人群获取疫情防控知识的渠道的对应分析

2.2.1 不同区域人群获取疫情防控知识的渠道的对应分析

（1）首先对频数进行个案加权，然后按照步骤操作进行对应分析[6-9]，过程不再展示。

（2）结果分析。对应表分别展示每个特征和每个渠道的频数分布，如表1所示。

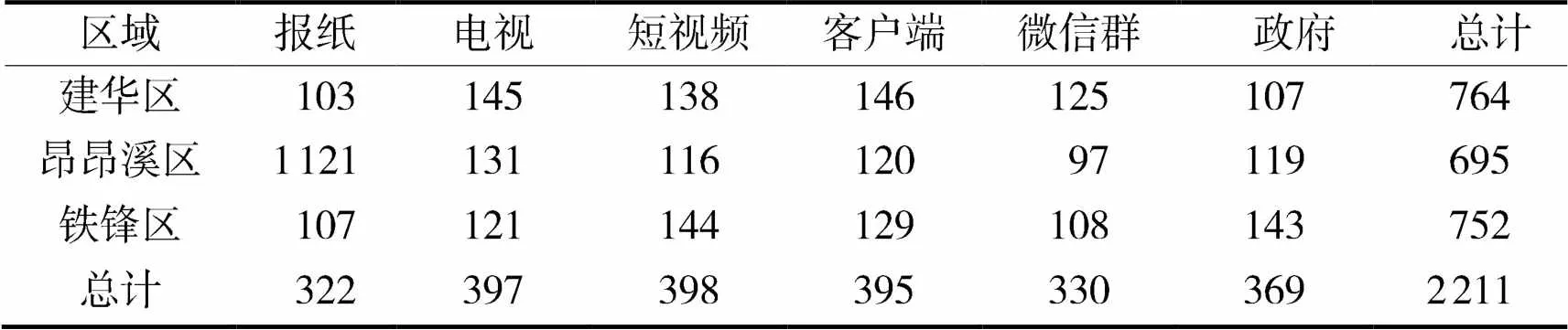
表1 对应表

模型摘要表自由度为10。首先观察卡方检验的结果。如表2所示，卡方值为13.730，= 0.186，卡方检验结果不显著，表明此次分析的两个名义变量（特征和渠道）是完全独立的，不能够进行对应分析，说明不同区域在获取疫情信息的渠道上并没有显著的区别[10-11]。

表2 总结

2.2.2 不同性别人群获取疫情防控知识的渠道的对应分析

由于性别群体仅有两个维度，无法进行对应分析，采用卡方分析的方法进行检验。

（1） 交叉表。交叉表统计了各个维度的频数分布，如表所示。

表3 渠道交叉制表

（2）卡方检验。有效回答数量为2091，卡方值为23.263，<0.001，卡方检验结果显著，表明男女性别的不同确实会影响获取疫情信息的渠道，如表4所示。

（3）频数分布图。男性更多从电视、短视频、新闻客户端3个渠道获取疫情信息，女性则在各种渠道上相对平均，没有显著差异，如图2所示。

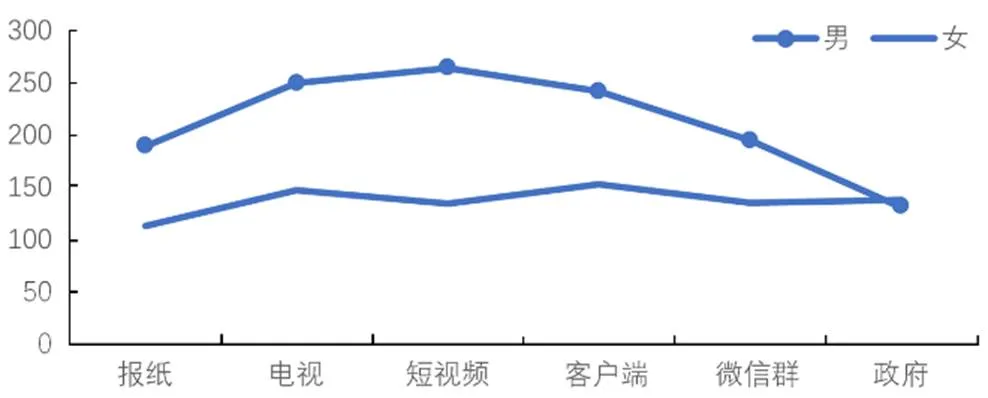
图2 频数分布图

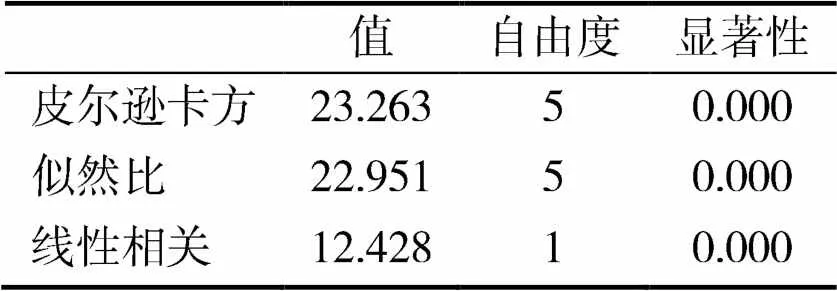
表4 卡方检验

2.2.3 不同年龄群体获取疫情防控知识的渠道的对应分析

首先对频数进行个案加权，然后按照步骤操作进行对应分析，过程不再展示。

（1）对应表。交叉统计表，分别展示每个特征和每个渠道的频数分布，如表5所示。

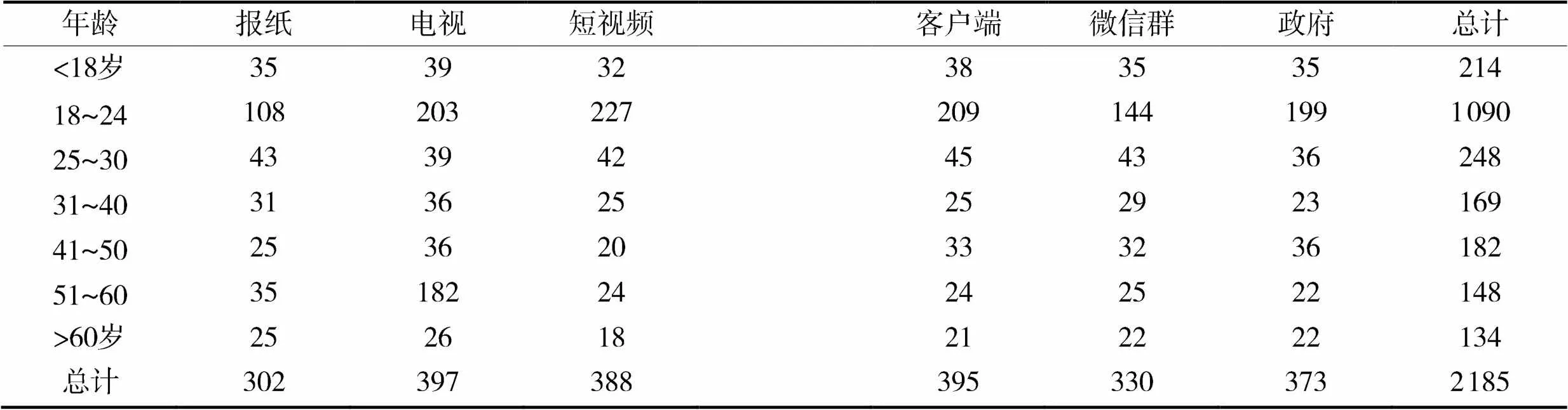
表5 对应表

（2）模型摘要表，自由度为30。首先观察卡方检验的结果，卡方值为61.626，= 0.001卡方检验结果显著，表明此次分析的两个名义变量—特征和渠道是不完全独立的，存在一定关系，能够进行对应分析，这和前面交叉表卡方检验结果一致，如表6所示。

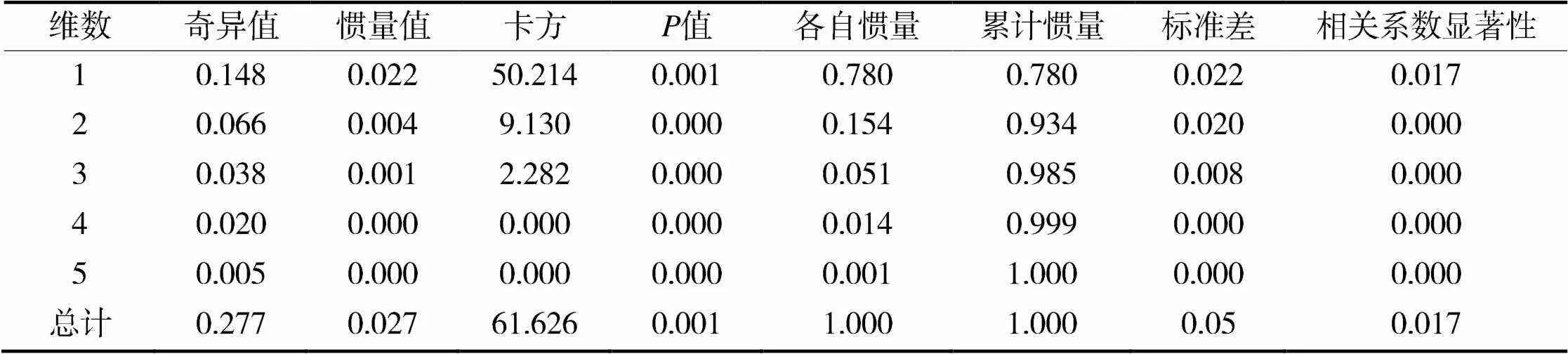
表6 总结

卡方检验通过之后，再来解读对应分析的其他结果更有意义。

摘要表数据表明，前两个维度累积惯量可解释93.4%的信息，效果非常不错，此次分析较成功。

图3 对应图

（3）行列点总览。依据行列点总览表在不同维度的得分，如表7, 8所示，可以绘制出对应图。

根据渠道和特征的距离远近来判断相关程度。显然，18岁以下、31～40以及60岁以上距离微信群较近，说明这3个年龄段的人群大多通过微信群获取疫情信息；18～24岁距离新闻客户端、政府新闻发布以及短视频平台较近，说明他们主要通过新闻客户端和政府新闻发布来获取疫情信息[12-13]。其余距离均较远，不存在高度的相关影响，如图3所示。

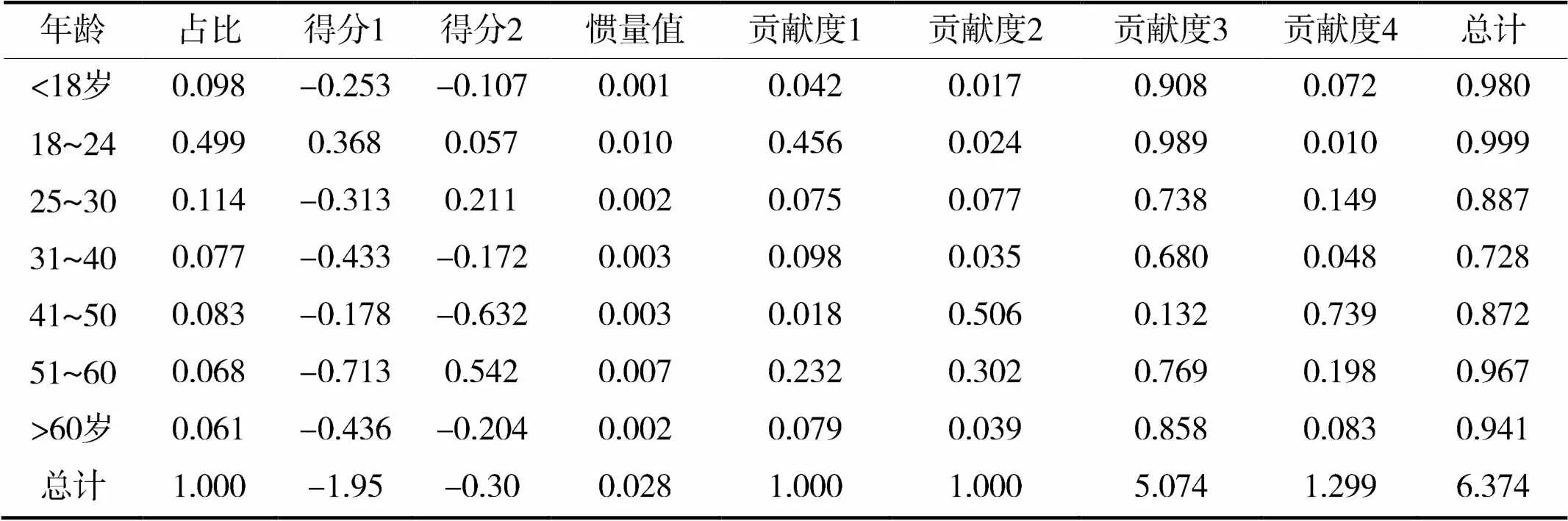
表7 行总览表

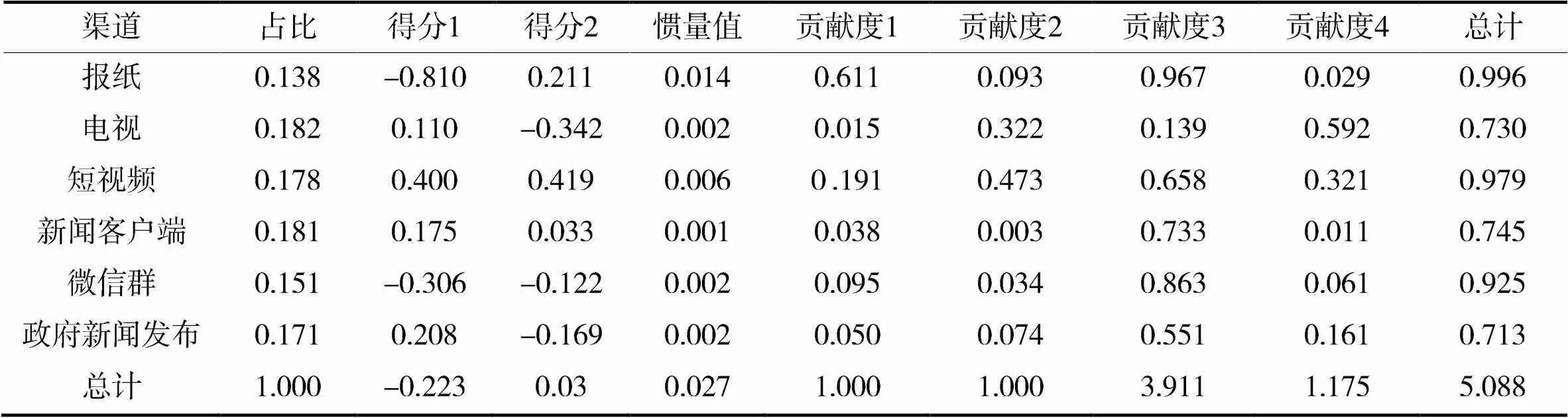
表8 列总览表

3 结论

COVID-19疫情在齐齐哈尔市发生后，引发的公共卫生以及社会问题已经引起人们的关注，但它对齐齐哈尔市不同人群的影响却尚未报道。本次调查对于在COVID-19疫情期间齐齐哈尔市不同群体获取疫情防控知识的渠道有了较为详细的了解。齐齐哈尔市被调查对象都积极通过各种渠道去了解疫情防控知识，这些渠道都不同程度上给被调查对象提供了他们想要了解的疫情防控知识，但由于区域、性别、年龄等因素的影响，不同群体了解疫情防控知识的渠道也不完全一致，所以说这些因素对人群了解疫情防控知识的渠道有着重要的影响。

[1] 陈重远，张大双，张习春，等. 基于主成分分析和聚类分析对籼稻资源品质性状的综合评价[J/OL]. 分子植物育种，(2021-09-16)[2021-09-17]. http://kns.cnki.net/kcms/detail/46.1068.S.20210916.1053.018.html.

[2] 巩红禹，张士琦，王春枝. 基于分层平衡抽样的多目标代表性样本设计——以住户调查为例[J]. 统计与信息论坛，2021, 36(02): 36-44.

[3] 马少勇，陈燕，王方方，等. 新冠肺炎流行期间医学生焦虑情绪及其影响因素[J]. 中国学校卫生，2021, 42(09): 1351-1355.

[4] 武汉发展战略研究院课题组，杜涛. 江岸区花桥街聚才社区疫情防控治理问卷调查分析[J]. 武汉学刊，2020(02): 4-5.

[5] 王小宁. 小域估计在问卷分割中的应用研究[J]. 统计与信息论坛，2021, 36(09): 3-10.

[6] 田美娜，牛蓓，张翠，等. 河北省某贫困县6～23月龄婴幼儿辅食喂养及其相关影响因素的多重对应分析[J]. 卫生研究，2021, 50(04): 665-668, 680.

[7] 宋俐，茅群霞，张雪峰，等. 对应分析在传染病疫情资料分析中的应用[J]. 江苏预防医学，2007(03): 4-8.

[8] 陈峰，杨树勤. 相应分析及其在多种疾病聚集性分析中的应用[J]. 中国卫生统计，1999, 16(02): 114-117.

[9] 罗珍胄，袁军，田丽闪，等. 性传播疾病疫情报告与临床科室的对应分析[J]. 实用预防医学，2013, 20(04): 429-431.

[10] 于飞，赵岩红. 基于卡方检验法的河北省农村电商发展影响因素分析[J]. 河北软件职业技术学院学报，2021, 23(02): 17-20.

[11] 魏雨晨，武斌，宋怡昕，等. 基于卡方分析的大学生疫情后心理健康问题[J]. 中阿科技论坛（中英文），2021(04): 191-193.

[12] 张持晨，吴一波，郑晓，等. 新冠肺炎疫情下公众的认知与行为——疫情常态化防控中的自我健康管理[J]. 科学决策，2020(10): 44-59.

[13] 熊腾琼，郭声敏，陈佩云，等. 公众对新型冠状病毒肺炎知信行现状调查及影响因素分析[J]. 现代医学，2020, 48(08): 1040-1045.

Analysis on the situation of prevention and control of COVID-19 among different populations in Qiqihar

ZHANG Quan，ZHENG Peng-hui，YU Shi-hang，GUAN Bao-ling

(College of Science, Qiqihar University, Heilongjiang Qiqihar 161006, China)

In order to understand the channels through which different groups of people in Qiqihar area can obtain knowledge about the prevention and control of the new crown epidemic during the epidemic period of the new crown epidemic, this paper adopts a cluster sampling method to conduct a sample survey of different populations in the Qiqihar area. Public health and education on the prevention and control of emerging infectious diseases provide theoretical basis.

COVID-19 epidemic；prevention and control；questionnaire

2021-04-01

黑龙江省教育厅项目（135509127）

张权（1978-），男，黑龙江齐齐哈尔人，副教授，博士，主要从事应用统计研究，zhangquan122400@163.com。

O213.9

A

1007-984X(2022)02-0091-04