工业区块链中基于CUDA的数据并行处理方法*

陈 强,谭 林,王云丽,肖 靖

(1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.湖南天河国云科技有限公司，湖南 长沙 410100)

1 引言

随着传感器、嵌入式芯片和人工智能等技术的发展，工业生产过程时刻在产生海量的数据，比如生产设备的运行环境、机械设备的运转状态、生产过程中的能源消耗、物料损耗等。使如此大规模的工业数据发挥其价值的关键环节在于数据的流通[1]。然而，如何使工业数据在不同企业间或同一企业的不同部门间安全、高效地流通是目前面临的首要问题。数据交易是数据流通的具体表现形式之一。在传统的数据交易系统中，一般存在数据拥有者、数据需求者及中间商3种角色。中间商的存在能给数据拥有者和数据需求者提供一个可信的交易环境，从而使双方能有效地进行数据交易[2,3]。然而，中间商的存在也给数据交易带来了复杂的交易流程、较高的交易费用以及信用依赖。因此，利用区块链技术去中心化、不可篡改和可溯源的优势，可以通过工业区块链交易系统提供可信的交易环境，使数据拥有者和数据需求者在没有可信中间商的情况下依然能够安全、有效地完成交易[4,5]。但是，由于区块链本身的局限性，区块容量较小不足以将大数据文件直接存储到区块。比如，在比特币中一个区块的最大容量只有6 MB左右，在Fabric中一个区块的最大容量也只有100 MB左右。因此，一般的解决方法是将源数据的哈希值或者源数据的存储地址等作为元数据存储到区块中，源数据本身则存储在云端或本地，从而形成链上存元数据、链下存源数据的存储方式[6-10]。但是，这样的做法在工业区块链中也存在以下2点不足：一是由于串行计算哈希值所需的时间随着数据量的增大而线性增长，因此，串行计算这种方式在工业区块链中难以满足大规模数据高效上链的需求；二是由于源数据本身没有存储到区块链，在交易时数据需求者无法确认源数据是否被篡改。所以，本文将重点研究基于CUDA的数据并行处理方法来提高大规模工业数据上链的效率，并在数据交易双方之间构建有效的数据完整性验证模型，使数据需求者在交易时就能够确认源数据本身的完整性。

在区块链系统中，将源数据存储到区块链时，其处理过程可以分为2个阶段：第1阶段包括业务数据处理和数据序列化等，第2阶段包括广播、打包和共识等。在业务数据处理步骤中，针对大数据文件一般是在CPU平台上利用OpenSSL等标准库计算其哈希值[11,12]。这些计算方法都是将大规模工业数据当作一个整体串行计算其哈希值，计算速度相对较慢。在区块链中，不论是将大数据文件当作一个整体来获得其哈希值，还是将大数据文件分块来获得其哈希值，只需计算所得的哈希值与大数据文件一一对应，上述2种方式获得的哈希值都可作为元数据存储到区块链。因此，本文针对工业数据规模大的特点，利用GPU在单指令多数据方面的计算优势[13-16]，设计了基于CUDA的数据哈希值并行计算方法，对工业数据实施了分块、哈希值并行计算等处理，以提高大规模工业数据哈希值的计算效率。

在传统的数据完整性验证方案和基于区块链的数据完整性验证方案中，都是持有签名私钥的数据拥有者或可信第三方向云服务商验证源数据的完整性[17-22]。然而，在工业区块链数据交易系统中构建的数据完整性验证模型中，持有签名私钥的数据拥有者是作为证明者出现的。因此，当数据需求者向数据拥有者验证源数据的完整性时，数据拥有者可能利用签名私钥向数据需求者提供伪造的证明信息，因为链上存元数据、链下存源数据的方式只能确保元数据不被篡改，而无法使数据需求者在交易时确认源数据本身的完整性。数据需求者只有在交易得到源数据本身后，才能验证源数据的完整性[23-25]。对于大数据文件的交易，如果数据拥有者不小心或故意篡改了源数据，那么数据需求者付出较大的通信代价得到的却是无用的数据。因此，如果在传输大规模工业数据前就能够确认其完整性，可以减小上述无意义交易带来的通信代价。所以，本文在现有的数据完整性验证方案上，将签名信息构建成默克尔哈希树并把默克尔根存储到区块链。在验证源数据完整性前，首先验证签名信息，避免用伪造的签名信息去验证源数据完整性，从而使数据需求者能够有效地验证源数据的完整性。

综上所述，通过基于CUDA的数据并行处理方法和两方完整性验证模型可以实现：

(1)通过合理的数据分块、线程布局等手段，使大规模工业数据哈希值的计算效率可以得到较明显的改善，提高了大规模工业数据上链的效率。

(2)在数据拥有者持有签名私钥的特殊情形下，通过区块链不可篡改、可溯源等特性，数据需求者仍可对数据拥有者提供的源数据进行有效的完整性验证。

2 基于CUDA的数据并行处理方法

基于SHA256哈希函数的原理，本文设计了基于CUDA的数据并行处理方法。SHA256函数的实现主要由以下4个算法构成[26]：

(1)PaddingChars(·)：首先对源数据进行分块，然后分别对数据块进行填充，使填充后的数据块长度为512的倍数，数据块长度用二进制位表示。

(2)Convert(·)：将填充后的每个数据块划分成M组长度为512位的数据，然后将每组数据转换成16个32位的无符号整数。

(3)Expand(·)：将16个32位无符号整数扩展成64个32位的无符号整数。

(4)Compress(·)：对每个数据块循环M次，每次基于64个32位的无符号整数计算中间哈希值，循环结束后得到的中间哈希值即为最终的哈希值。

本文设计的基于CUDA的数据并行处理方法如算法1所示，主要设计思路如下所示：

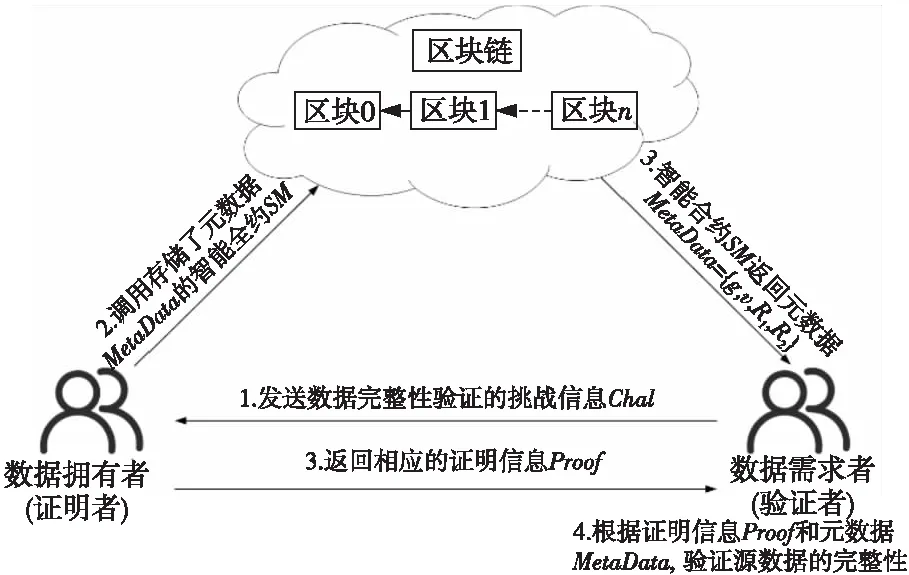
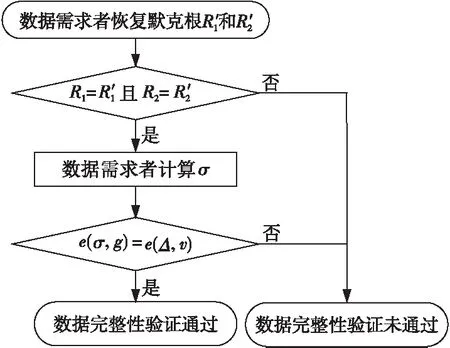
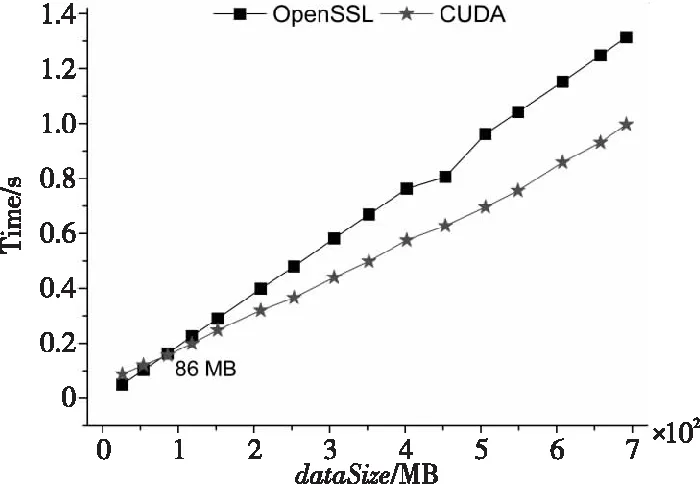
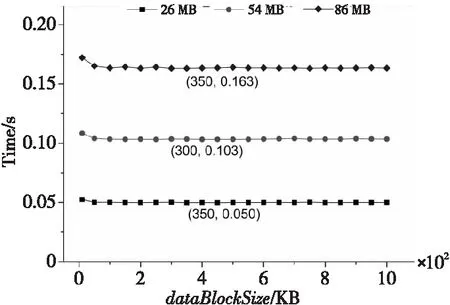
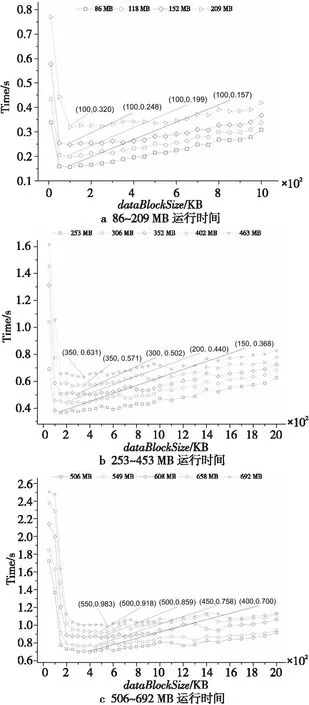
(1)当源数据的大小dataSize

(2)当dataSize≥dataSizeThreshold时，由于GPU内存大小的限制，需要分批将源数据从主机端复制到GPU内存。在每次将数据复制到GPU内存后，对数据进行分块，基于数据块大小dataBlockSize并发相应的线程数并行计算数据块哈希值、构建默克尔哈希树T1，并将T1从GPU内存复制到主机端，对应算法1第6～10步。

算法1基于CUDA的数据并行处理方法

Input:Source fileF。

Output:Merkle hash treeT1。

1:IfdataSize

2: Dividing source dataFintonblocks anddataBlockAmount=n;

3:fori=1 tondo

Computing hash value of data blocks by CPU;

endfor

4: Constructing Merkle hash treeT1by CPU；

5:else

6:fori=0 tocopyTimesdo

7: (1)Copy data from host memory to GPU device memory;

(2)Dividing source dataFintonblocks anddataBlockAmount=n,threadAmount=n;

(3)Parallelly employingnthreads to executePaddingChars(·),Convert(·),Expand(·)andCopmpress(·);

8:endfor

9: Constructing Merkle hash treeT1on GPU;

10: Copy hash values from GPU memory to host memory;

11:endif

12:returnMerkle hash treeT1.

影响本文设计的因素主要有以下3个：(1)源数据的大小dataSize；(2)GPU内存的大小GPUMemorySize；(3)并行计算时的数据块大小dataBlockSize，它与SHA256函数的原理、GPU的CUDA核心数量、共享内存大小和寄存器文件大小等相关。

因素1源数据大小。

源数据大小dataSize直接决定是由CPU串行还是GPU并行来计算数据块的哈希值。因为源数据在主机端和GPU之间复制需要通信时间，并且CPU单线程的运算速度远远高于GPU单个线程的，所以，并不是所有大小的源数据都适合利用GPU来计算哈希值和构建默克尔哈希树。定义CPU计算数据块哈希值并构建默克尔哈希树的时间为TCPU，对应算法1中第1～4步的运行时间；把源数据从主机端复制到GPU的时间为Th→GPU，对应算法1中第7(1)步的运行时间乘以copyTimes；利用GPU计算各个数据块哈希值并构建默克尔哈希树的时间为TGPU，对应算法1中第6～9步的运行时间；将数据块哈希值从GPU传回主机端的时间是TGPU→h，对应算法1中第10步的运行时间。随着源数据的增大，TCPU、Th→GPU、TGPU、TGPU→h都将增大，但是TCPU的增大速度大于TGPU的增大速度，并且TCPU远大于Th→GPU和TGPU→h。因此，当源数据的大小dataSize超过阈值dataSizeThreshold时，式(1)所示的不等式将成立：

TCPU>Th→GPU+TGPU+TGPU→h

(1)

所以，当源数据的大小dataSize

因素2GPU内存大小。

由于GPU内存大小GPUMemorySize的限制，当源数据足够大时，不能一次性把源数据从主机端复制到GPU内存。定义每次可从主机端复制到GPU内存的数据最大值为dataSizePerCopyMB。由SHA256函数原理可知，在执行Expand(·)算法时需要的GPU内存空间将达到最大值，此时，输入数据占用的内存空间为dataSizePerCopyMB，输出数据占用的内存空间为4×datasizePerCopyMB。由此可知，dataSizePerCopy应满足式(2)：

5×dataSizePerCopy

(2)

则将源数据复制到GPU内存的次数CopyTimes如式(3)所示：

copyTimes=ceil(dataSize/dataSizePerCopy)

(3)

其中，ceil(·)函数表示向上取整。

因素3数据块大小。

在利用GPU并行计算时，如何对源数据进行分块对哈希值的计算效率非常重要。如果分块数量过少，将导致GPU中并行程度不够，从而无法发挥GPU的并行计算优势；如果分块数量过多，由于GPU硬件资源的限制，没有足够多的线程来支撑哈希值计算，反而会降低计算效率。在本文方法中，数据块的大小dataBlockSize主要由SHA256函数的原理及GPU的硬件资源决定。

在SHA256函数原理方面，如何对数据块进行填充是关键。假设源数据F的长度L(L以二进制位数量表示)为：L=512k+b，其中k，b都是非负整数。在执行PaddingChars(·)算法时，对源数据F的填充分2种情形进行：

(1)情形1：如果 0 ≤b<448，则填充后的结果如图1a所示。

首先，需要填充1个二进制数1和448-b-1个二进制数0。然后，再填充用64位二进制数表示的源数据长度L。完成填充后，数据的长度L′=512(k+1)。

(2)情形2：如果 448≤b<512，则填充后的结果如图1b所示。

首先，需要填1个二进制数1和512-b-1+448 个二进制数0。然后，再填充用64位二进制数表示的源数据长度L。完成填充后，数据的长度L′=512(k+2)。

Figure 1 Schematic diagram after filling the source data

由此可知，填充后情形2比情形1多了512位数据，在之后计算哈希值的过程中，每个数据块执行Convert(·)、Expand(·)和Compress(·)算法时都会多1次计算，并且每个数据块多余的填充数据将占据更多的CPU或GPU内存。所以，在进行数据分块时，数据块的大小应满足情形1。

在GPU硬件资源方面，CUDA核心数量、寄存器文件的大小等都会限制并行计算中的线程数量，而线程的数量会直接影响源数据如何进行分块。在有限的硬件资源下，GPU并行计算性能的发挥主要依赖内核网格和线程块的配置。配置网格和块的大小时的准则主要有：(1)保持每个线程块中线程数量是线程束大小的倍数；(2)线程块的数量要大于流式多处理器的数量，并且是流式处理器的倍数，保障在GPU中有足够多的并行。

3 两方数据完整性验证模型设计

本文设计的两方数据完整性验证模型由数据建立和验证2个阶段构成。

3.1 建立阶段

源数据处理阶段的流程如图2所示。首先，利用本文提出的数据并行处理方法对源数据F进行分块，可以得到n个数据块{m1,m2,…,mn}，其中,mi∈ZP,1≤i≤n，Z为整数集，P为一个大素数。同时，利用该方法计算数据块的哈希值并构建默克尔哈希树T1。默克尔哈希树T1的构建过程如下所示：(1)并行计算数据块的哈希值；(2)将相邻数据块的哈希值两两拼接在一起再并行计算哈希值，如果拼接时哈希值的数量为奇数，则对尾部的哈希值进行复制；(3)循环第2步操作，直至得到最后1个哈希值默克尔根R1。

Figure 2 Flow chart of source data processing

然后，令e:G1×G1→G2为一个双线性映射，其中，G1和G2为乘法循环群，g是G1的生成元。数据拥有者随机选择一个数α∈ZP，计算v=gα，并把α作为私钥SK，v作为公钥PK。接着，数据拥有者随机选择u∈G1，并计算数据块{m1,m2,…,mn}的签名信息Φ={σ1,σ2,…,σn}，σi=(H(mi)·umi)α,i=1,2,…,n，H(mi)为第i个数据块的哈希值，并对签名信息构建默克尔哈希树T2，其构建过程与T1相似，最终同样可以得到其相应的默克尔根R2。

最后，数据拥有者将源数据的元数据MetaData={g,v,R1,R2}存储到区块链上的智能合约SM中。

3.2 验证阶段

如图3所示，在本文的完整性验证模型中，数据拥有者和数据需求者两方实体分别扮演证明者和验证者角色。当进行数据完整性验证时，首先，数据需求者向数据拥有者发送挑战信息Chal;然后，数据拥有者根据挑战信息Chal计算相关证明信息Proof，并同时调用智能合约SM;最后，数据需求者根据数据拥有者返回的证明信息和元数据信息验证源数据的完整性。

Figure 3 Integrity verification of source data

数据需求者从集合{1,2,…,n}中随机选择c个元素,组成子集S={s1,s2,…,sc}，其中1≤s1≤s2≤…≤sc≤n。对于每一个si∈S，在ZP中随机选择一个数vi与之对应，形成V={vs1,vs2,…,vsc}。首先，数据需求者将挑战信息Chal={S,V}发送给数据拥有者，即图3的步骤1。数据拥有者在接收到挑战信息Chal后，根据式(4)计算μ和Δ：

(4)

其中，mi为第i个数据块，vi为随机数，H(mi)为第i个数据块的哈希值，u为数据拥有者在建立阶段选择的随机数。接着，数据拥有者调用存储了元数据MetaData={g,v,R1,R2}的智能合约SM(即图3的步骤2)，并将证明信息Proof={H(mi),A1,Φ′,A2,Δ}发送给数据需求者(即图3的步骤3)，其中，s1≤i≤sc，H(mi)为第i个数据块的哈希值;Φ′为数据块的签名信息子集,Φ′={σs1,σs2,…,σsc};A1为恢复默克尔根R1的辅助信息;A2为恢复默克尔根R2的辅助信息。A1和A2的具体含义如图4所示。假设将源数据分为4个数据块{m1,m2,m3,m4}，基于这4个数据块构建默克尔哈希树得到的默克尔根为R。在只拥有数据块m2的情况下，由辅助信息A={H(m1),H34}恢复默克尔根R的计算过程如下所示：

(1)由数据块m2计算得到H(m2)；

(2)由H(m1)和H(m2)计算出H12；

(3)由H12和H34可恢复得到默克尔根R。

Figure 4 Recovering Merkle root with auxiliary information

数据需求者在接收到证明信息Proof和元数据MetaData后进行验证(即图3的步骤4)，其详细的验证流程如图 5所示。在第1步验证中，数据需求者根据{H(mi),A1,A2}恢复默克尔根R′1和R′2，并判断R′1和R′2是否与MetaData中的默克尔根R1和R2相等。如果不相等，则认为证明信息是伪造的,证明信息无法证明源数据的完整性。如果相等，则继续第2步验证，数据需求者根据数据块的签名信息子集Φ′={σs1,σs2,…,σsc}和V={vs1,vs2,…,vsc}通过式(5)计算σ:

(5)

再根据证明信息Proof中的Δ和元数据中的{g,v}，验证式(6):

e(σ,g)=e(Δ,v)

(6)

是否成立。如果成立则认为数据是完整的，如果不成立则认为源数据已经被改动。式(6)中g是G1的生成元，v=gα是公钥，这2个数据都存储在区块链上的智能合约SM中，是不可篡改的。σ是由数据需求者根据签名信息Φ′和数据集V={vs1,vs2,…,vsc}计算所得。Δ是由数据拥有者根据挑战信息Chal计算所得。

Figure 5 Flow chart of data integrity verification

4 结果分析与讨论

4.1 数据文件哈希值计算对比实验及结果分析

此部分实验的主要目的是获得本文并行处理方法中的参数dataSizeThreshold、threadAmount、copyTimes以及该方法的运行效率。实验计算平台的CPU和GPU信息如表 1所示。

由于GPU内存大小为4 GB，由式(2)可知其应满足式(7)：

dataSizePerCopy≤819.2

(7)

因此，可以将dataSizePerCopy设置为700 MB。然后，由式(3)计算出将源数据由主机端复制

Table 1 Basic information of CPU and GPU

到GPU内存的次数copyTimes,如式(8)所示：

copyTimes=ceil(dataSize/700)

(8)

当源数据大于700 MB时，需要分copyTimes次处理源数据。当每次处理相同大小的源数据时，并行处理方法所用时间几乎相同。因此，本文在电网日常监测数据中选取大小分别为 {26,54,86,118,152,209,253,306,352,402,453,506,549,608,658,692}(单位为MB)的源数据进行分块，其中152 MB以下以30 MB左右为步长，152 MB以上以50 MB左右为步长。26 MB～152 MB源数据的分块大小dataBlockSize∈{10,50,100,150,200,…,950,1 000}(单位为KB)，152 MB～692 MB源数据的分块大小dataBlockSize∈{50,100,150,200,…,950,1 000,1 100,…,1 600}(单位为KB)。然后，对不同大小的分块，利用基于OpenSSL的数据串行处理方法和基于CUDA的数据并行处理方法分别进行100次运算，得到每次运算时间后去掉其中的最大值和最小值，再求取运算时间的平均值。

2种方法的运算时间如图6所示。从图6可知，当源数据大小大于86 MB时，基于CUDA的数据并行处理方法的运算时间小于基于OpenSSL的数据串行处理方法的运算时间。所以，本文方法中的dataSizeThreshold设置为86 MB。当dataSize≤86 MB时，选择串行方法处理源数据；当dataSize≥86 MB时，选择并行方法处理源数据。

基于图6的运行时间，本文所提出的并行处理方法相较于基于OpenSSL的数据串行处理方法的加速效率如图7所示。显然，源数据越大，基于CUDA的数据并行处理方法的加速效果越好。当源数据大小大于253 MB时，加速效率在22%以上，并且在等于506 MB时，加速效率达到最大值27.7%。

Figure 6 Comparison of the running time of two methods

Figure 7 Acceleration efficiency of CUDA-based data parallel processing method

当源数据大小小于86 MB时，本文使用基于OpenSSL的串行处理方法。针对不同大小源数据的运行结果如图8所示，图8中标示了最短运行时间。从图8可知，对于不同大小的源数据，该方法的运行效率在数据块大小为10 KB时较低，而在数据块大于10 KB时运行效率变化不大，因此dataBlockSize可根据实际需求设置为100 KB以上的任意值。

Figure 8 Running time of OpenSSL-based data serial processing method

当源数据大小大于86 MB时，本文使用基于CUDA的并行处理方法。不同大小源数据的运算结果如图9所示，图9中标示了最短运行时间。从图9可知，当dataBlockSize太小或者太大时，数据并行处理方法的运行时间较长、效率较低。这是因为当源数据的分块太小时会产生大量的数据块，GPU硬件资源的限制导致无法支持过多的并行线程，使得运行时间极速增加；当数据块太大时，并行线程太少导致无法发挥GPU并行计算的优势，也会使得效率较低。

Figure 9 Running time of CUDA-based data parallel processing method

根据图9可以得到不同大小源数据的最佳dataBlockSize取值，因此针对不同源数据可以得到具体分块策略，如图10所示。例如，在区间(250,300]MB时，dataBlockSize设置为150 KB，对应图9b中253 M曲线的最少运行时间的分块大小为150 KB。依次类推能得到不同大小源数据的合适的分块大小dataBlockSize。由不同大小的dataBlockSize可以计算出每次执行基于CUDA的数据并行处理方法时使用的线程数量threadAmount,如式(9)所示:

threadAmount=ceil(700(MB)/

dataBlockSize(KB))

(9)

其中，ceil(·)表示向上取整。

综上所述，本文提出的并行处理方法，基于所用实验平台，需将dataSizePerCopy设置为700 MB，即在源数据大于700 MB时分批传输到GPU端进行处理。当源数据大于86 MB时，在GPU端的运行效率优于在CPU端的运行效率，因此将dataSizeThreshold设置为86 MB。针对不同大小的源数据，数据分块策略如图10所示，根据不同大小的源数据选择不同大小的分块，从而配置不同的线程布局以获得较好的运行效率。

Figure 10 Blocking strategy of different source data for CUDA-based data parallel processing method

4.2 两方数据完整性验证模型安全性分析

与传统完整性验证不同的是，在本文的完整性验证中数据拥有者是持有签名私钥的。在不做保护措施的情形下，数据拥有者可以利用签名私钥伪造证明信息使完整性验证通过。因此，本文在图5的第1步验证中，首先验证了签名信息的默克尔根R2和R′2是否相等。如果不相等，那么我们就直接认为源数据已经被篡改。如果相等，那么可以确定签名信息Φ′={σs1,σs2,…，σsc}是没有被篡改的，为下一步验证提供了保证。

综上所述，在数据拥有者持有签名私钥的特殊情形下，本文设计的数据完整性验证方案能够在数据拥有者不小心或故意改动源数据的情况下发现数据变动，及时终止接下来无意义的交易步骤。在本文数据完整性验证方案中，若数据拥有者将数据存储到云端而本地无备份时，只需将证明者替换成云服务提供者即可在数据需求者和云服务商之间对源数据进行完整性验证。

5 结束语

针对工业数据规模大的特点，本文提出了一种基于CUDA的数据并行处理方法。在源数据大小大于86 MB时，该方法针对不同大小的源数据利用给出的分块策略，使运行效率优于基于OpenSSL的数据串行处理方法。并且，源数据越大，并行处理方法的运行效率越好。同时，基于此方法提出的两方完整性验证模型即使在数据拥有者持有私钥的特殊情形下，数据需求者依然能够在得到源数据之前、只得到元数据的情况下，有效地验证源数据的完整性，避免因传输无用数据而付出的通信代价。