分块矩阵在矩阵证明题中的应用

赵中华

南京财经大学应用数学学院 南京 210046

分块矩阵在矩阵证明题中的应用

赵中华

南京财经大学应用数学学院 南京 210046

结合矩阵中的一些结论，讨论分块矩阵在矩阵证明题中的应用。例题说明分块的方法是矩阵证明题中较简捷、有效的方法。

分块矩阵；秩；初等变换

Author’s address Institute of Applied Maths, Nanjing Univ. of Finance & Economics, Nanjing, China 210046

在高等代数中，矩阵分块的方法对矩阵证明题来说是一种很好的方法。本文结合矩阵的初等变换、矩阵秩的有关性质，对相关矩阵进行分块或构造相关的分块矩阵，讨论分块矩阵在证明题型中的应用。

先以常用的2×2的分块矩阵为例，给出几个与分块矩阵相关的定义与性质。

由定义1可得，分块初等矩阵具有以下形式：

其中P、Q分别是m阶和n阶可逆方阵。

注：在使用分块初等矩阵乘法时，要注意所作分块必须使得分块乘法的运算能进行。

由定义1，给出分块初等矩阵的性质。

性质1：对分块矩阵进行一次行（列）初等变换，相当于左（右）乘一个相应的分块初等矩阵。

性质2：分块初等矩阵是可逆矩阵，分块初等变换不改变矩阵的秩。

性质3：对一个分块矩阵左（右）乘一个分块初等矩阵，不改变原分块矩阵的秩。

1 分块矩阵在秩的证明题中的应用

证明方法：利用分块初等矩阵的性质和秩的性质。秩的2个性质：

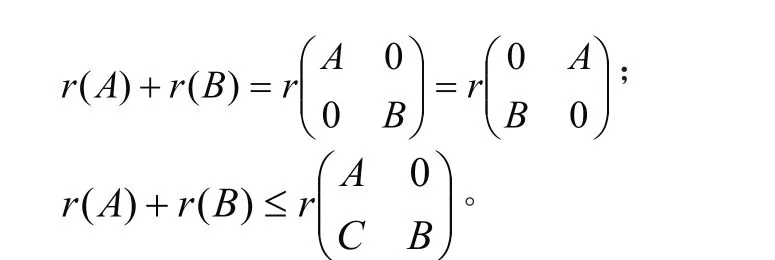
1.1 在秩的不等式证明中的应用

例11 设 A=As×n, B=Bn×m。

证明：r( A) +r( B ) −n ≤r( A B ) ≤ min{r( A), r( B)}。

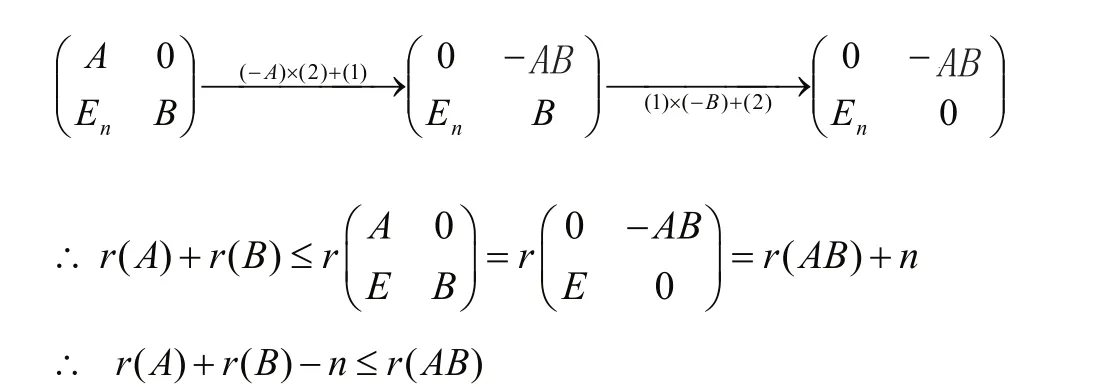
故r( A B ) ≤r( C ) =r( A)。

注：本例中，若AB=0， 则r ( A)+ r(B)≤n。

1.2 在秩的等式证明中的应用

例22 A设为n阶方阵，证明：

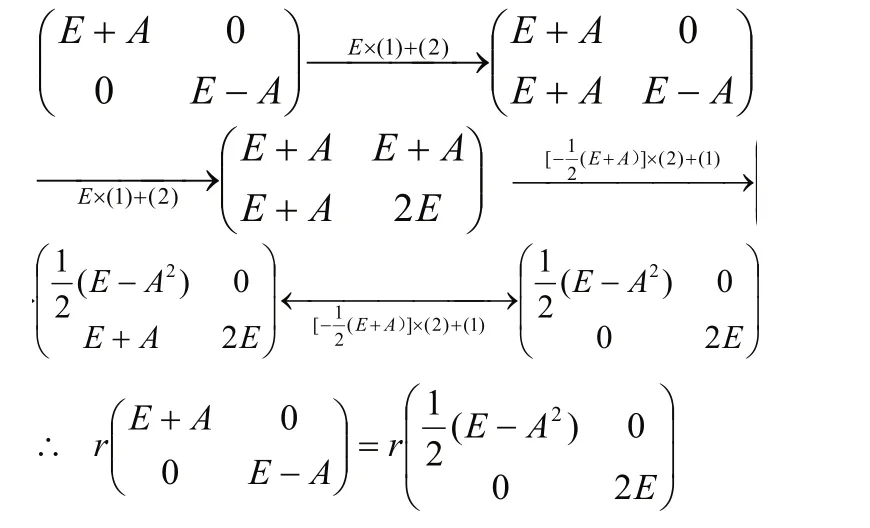
即：r(E+A)+r(E−A)=r(E−A2)+r (E)=r(E−A2)+n

∴r(E+A)+r (E−A)=n⇔A2=E

2 分块矩阵在矩阵存在性问题中的应用

证明方法：利用矩阵秩的化简结论。

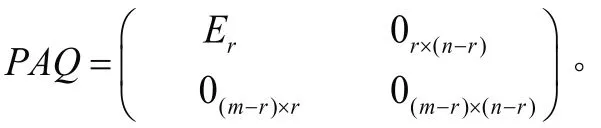
例33 设 B = Bm×n，且 r( B )=n。

证明：存在 A = An×m，且 r( A )=n，使 ABB = En。

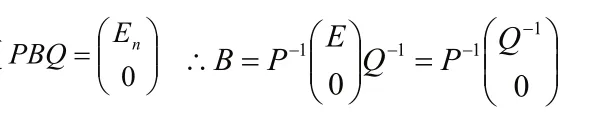
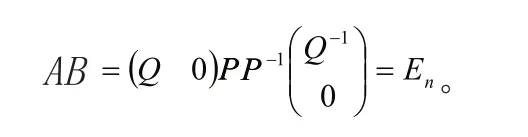
3 分块矩阵在矩阵分解中的应用

证明方法：利用矩阵秩的化简结论。

例44 证明：任一方阵A都可写为A=BC，其B2=B，C可逆。

证明 设 rAr =)( ，则存在n阶可逆矩阵P，Q，使

例5（满秩分解） 证明：对任意m×n阶矩阵A，设 r( A )=r，则有A=H L，其中 H=Hm×r, L=Lr×n，且r(H)= r (L)=r 。

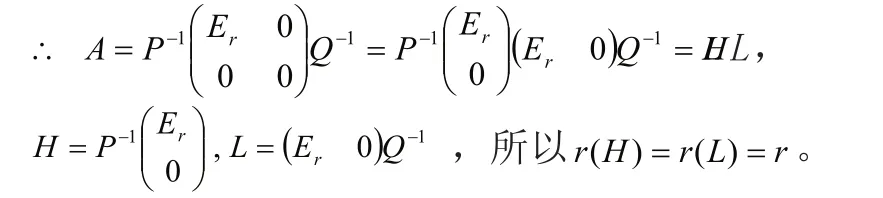
4 分块矩阵在矩阵行列式相关问题中的应用

证明方法：利用分块矩阵的初等变换及行列式的运算。

例66 设 A=Am×n,B=Bn×m,m≥n。

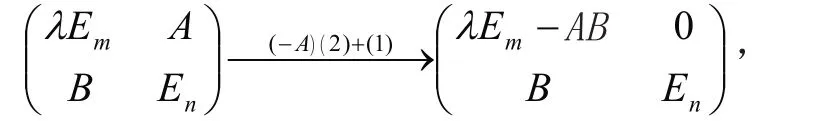
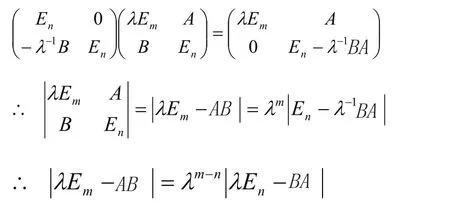
注：此题也可转化为证明秩的问题r(λEm−AABB)=m −n+r (En−BBAA)。

5 分块矩阵在矩阵求逆问题中的应用

证明方法：利用分块矩阵的初等变换及分块矩阵求逆的方法及结论。

所以，由分块矩阵的逆，可得：

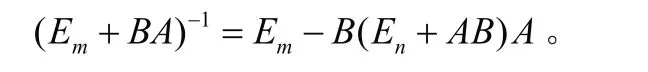
在高等代数中，利用分块的方法证明矩阵问题的题目还有很多，这里只是列举了其中的一些加以讨论。并且，有的例题也有其他的证明方法，这里不再一一给出。另外，分块的方法与齐次线性方程组解的结构相结合（一般是系数矩阵的列分块），也可以解决一些问题。例如，“若AB就可以用齐次方程组解的结构来证明。总之，由以上例子可以看出，矩阵分块在矩阵证明题中是一种较简捷、有效的方法。

[1]李守金,郭秀刚,牟树杰.分块矩阵的初等变换在行列式中的应用[J].中国教育技术装备,2009(11):91-94

[2]雷英果.分块矩阵及其应用[J].工科数学,1998,14(4):150-154

[3]王品超.高等代数新方法[M]].济南:山东教育出版社,1989

Application of Block Matrix in Proof of Matrix

//Zhao Zhonghua

The paper discusses the application of block matrix in the proof of matrix, combined with the conclusions of matrix. Examples show that the way of block is more effective and succinct in the proof of matrix.

block matrix; rank; primary transformation

O241.6

B

1671-489X(2010)09-0052-03

10.3969 /j.issn.1671-489X.2010.09.052

作者：硕士，讲师。