混凝土中爆炸应力波衰减规律的数值模拟研究*
2022-12-21孔祥振
高 矗,孔祥振,方 秦,王 银,杨 亚
(1. 陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007;2. 内蒙古财经大学,内蒙古 呼和浩特 010070)
混凝土广泛用于军民用防护结构中,在抗爆设计和毁伤评估时,重点关注在武器弹药爆炸等强动载作用下混凝土的应力波传播。在炸药爆炸近区,混凝土荷载具高幅值和短持时,呈现与静载作用下显著不同的强非线性、高应变率效应和高静水压力,这使分析混凝土中爆炸应力波(以下简称为爆炸波)衰减规律面临巨大的困难和挑战[1]。
爆炸实验成本高、周期长,且混凝土中传感器埋设和高幅值应力波测试较难,现有混凝土爆炸波衰减规律的实验相对较少。Gran 等[2]测定了球形装药在WES5000 混凝土(设计抗压强度为34.5 MPa[3])靶体中爆炸时不同距离的爆炸波曲线,并对比不同类型传感器测试结果,验证了实验数据的可靠性。Mu 等[4]对不同装药埋深时混凝土中爆炸波峰值衰减规律进行了实验研究,并结合量纲分析给出了C30 混凝土爆炸波峰值的预测公式。黄家蓉等[5]测得了柱形装药在C20 砂浆中的爆炸波,并利用AUTODYN 对实验进行了数值模拟,模拟结果与实验吻合较好。然而,混凝土中爆炸波的传播衰减涉及炸药能量释放、混凝土材料与爆轰产物的相互作用、强冲击波在介质中的传播等,理论研究难以全面反映这些过程。宗国庆[6]对混凝土介质的爆炸破坏效应(如开坑破坏)进行了较系统的分析并建立了相关公式。Tu 等[7]建立了柱形装药接触爆炸时混凝土中爆炸波预测的理论模型,但模型仅基于混凝土损伤破坏实验(如震塌破坏)进行验证,有待进一步验证可靠性。
数值计算方法的发展和计算效率的提升,使数值模拟逐渐成为研究混凝土中爆炸波的重要手段[8]。董永香等[9]利用LS-DYNA,模拟了平面爆炸波在半无限混凝土介质中的传播过程,认为应力波幅值衰减和材料损伤演化存在内在联系。赵凯等[10]模拟了集团装药产生的爆炸波在混凝土介质中的传播,阐明了装药形状对近区混凝土扩孔效应、应力波传播和混凝土损伤演化的影响。但是,因缺乏可靠的实验数据和高精度的数值模拟结果,尚未建立可靠的混凝土中爆炸波衰减规律的实用计算公式。
混凝土中爆炸波数值模拟的精度取决于许多因素,其中完善的混凝土材料模型、合理的数值算法和合适的网格尺寸是关键。在爆炸荷载作用近区,受高压和高应变率作用混凝土材料呈现近似流体特性,经典损伤塑性模型难以较好描述其时混凝土的力学行为。因此,普遍采用流体弹塑性模型,即分别采用强度面和状态方程,描述在冲击爆炸荷载下混凝土的偏量和球量行为。近年来,又开发了Kong-Fang 混凝土材料流体弹塑性模型(以下简称为Kong-Fang 模型)[11-15]。Kong 等[11]依据混凝土压力-体积应变和三轴压缩的实验数据,对比分析了常用的HJC 模型、RHT 模型、K&C 模型和Kong-Fang 模型等流体弹塑性模型对状态方程和最大强度面的预测效果,发现Kong-Fang 模型整体上优于其他3 种模型。Kong-Fang 模型具有良好的预测效果,其原因为:首先,以往模型高围压实验数据较少,Kong-Fang 模型在参数标定时补充了高围压下的相关实验数据;其次,Kong-Fang 模型通过关联流动法则考虑球量对偏量的影响,更符合高围压下的混凝土材料的响应状态。
混凝土中爆炸波传播的数值模拟过程涉及爆轰产物的膨胀飞散和混凝土的损伤破坏等,合理的数值算法需同时描述爆轰产物飞散以及混凝土材料的大变形。在描述混凝土靶体大变形时,Lagrange 算法需通过侵蚀算法解决网格畸变问题,导致爆轰能量发生较大耗散,无法有效地模拟爆轰产物和混凝土间的相互作用。Euler 算法可避免网格畸变问题而能模拟爆轰产物的大变形流动,但在界面运动追踪方面有些困难[8]。而ALE(arbitrary Lagrangian-Eulerian)算法不仅可以避免网格畸变问题,也能较好地追踪多种物质的界面[16],可较好地描述混凝土中爆炸波的传播衰减。
值得注意,武器弹药命中目标时的埋深常介于接触爆炸和完全内爆(自由场爆炸),变埋深条件下装药爆炸能量与混凝土介质的耦合形式和比例尚未有定论[16-17]。在美军技术手册TM5-855-1《常规武器防护设计基础》中,引入耦合系数(装药部分埋设爆炸与完全内爆在相同介质中产生的爆炸效应比),并给出混凝土中耦合系数与装药比例埋深的关系曲线。在计算爆炸波峰值、冲量和介质加速度等爆炸效应参数时,该手册均使用相同的耦合系数[18],而冲量型耦合系数与应力型耦合系数是有区别的[19]。Mandal 等[16]和Leong 等[20]指出,耦合系数与装药形状、介质强度和密度等均相关,因此,对不同爆炸效应参数采用相同耦合系数,有待商榷。
本文中,基于WES5000 混凝土中球形装药内爆实验[2],利用近年开发的Kong-Fang 混凝土材料模型[13-14]和LS-DYNA 中的多物质ALE 算法,研究混凝土中爆炸应力波的传播衰减规律,并采用量纲分析方法建立混凝土自由场中近区爆炸波峰值的计算公式。在此基础上,分析装药埋深对混凝土中爆炸波峰值分布和耦合系数的影响,建立变埋深时混凝土中近区爆炸波峰值应力的计算公式。
1 数值模型及验证
基于Kong-Fang 混凝土材料模型,先标定WES5000 和C100 混凝土的参数,再采用LS-DYNA 的多物质ALE 算法分析网格尺寸的收敛性,然后利用Gran 等[2]的实验数据验证数值模型结果。
1.1 材料模型及参数标定
Kong-Fang 模型参数主要包括强度面参数、状态方程参数和损伤参数[13-14],为确保爆炸波模拟的准确性,先根据已有混凝土静动态力学性能实验,重新标定WES5000 和C100 高强混凝土的状态方程和强度面参数。
Schmidt 等[3]、Gran 等[21]和Gebbeken 等[22]进行了WES5000 混凝土基本力学性能实验。利用静水压缩和平板撞击实验标定状态方程参数,利用三轴压缩实验标定强度面参数,如图1~2 所示。
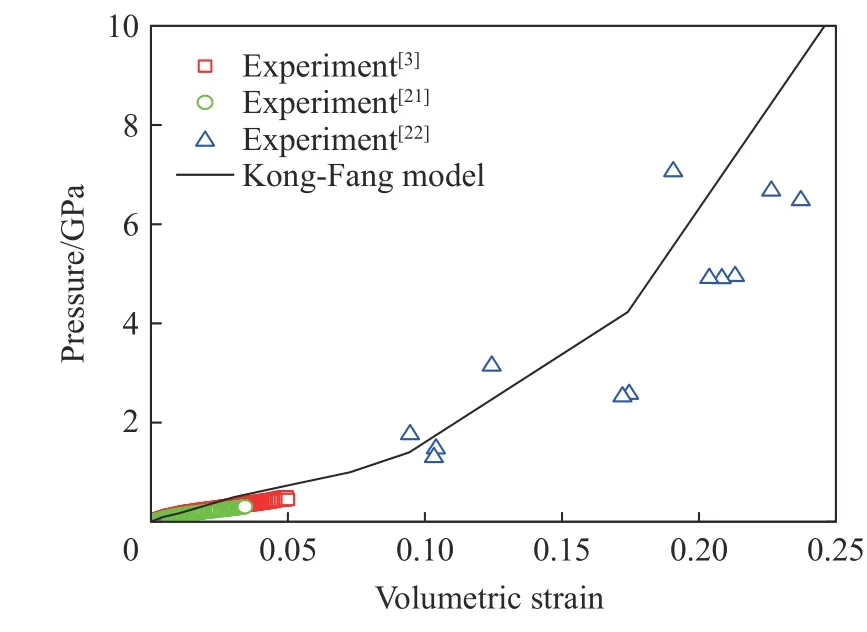
图1 WES5000 混凝土的状态方程Fig. 1 Equation of state for WES5000 concrete
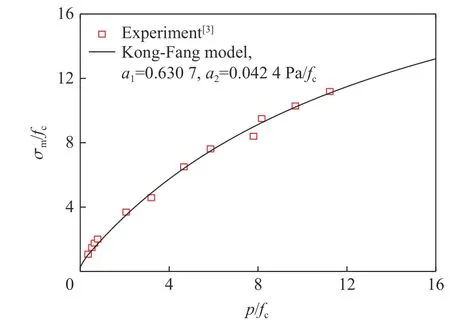
图2 WES5000 混凝土的强度面参数Fig. 2 Failure surface parameters for WES5000 concrete
对于C100 高强混凝土,采用Yang 等[15]对Kong-Fang 模型标定的超高性能混凝土状态方程(见图3);基于Williams 等[25]和Ren 等[26]的三轴压缩实验数据,标定了强度面参数(见图4)。
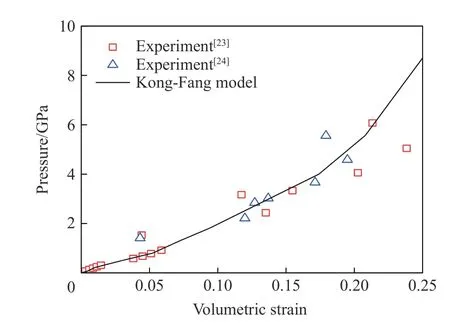
图3 C100 混凝土的状态方程[15]Fig. 3 Equation of state for C100 concrete[15]
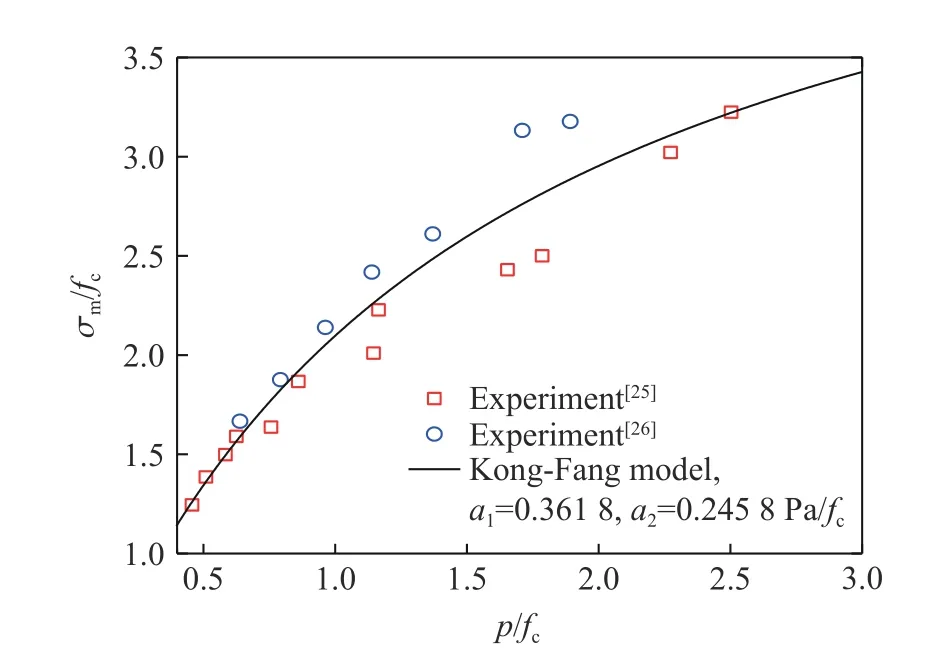
图4 C100 混凝土的强度面参数Fig. 4 Failure surface parameters for C100 concrete
WES5000 和C100 混凝土的其他参数,采用Kong-Fang 模型自动生成算法获得[12,14]。
采用Jones-Wilkins-Lee 状态方程描述B 炸药和TNT 炸药:

1.2 数值计算策略及网格收敛性分析
Gran 等[2]开展了0.454 kg 球形B 炸药在WES5000 混凝土中爆炸波传播的实验研究,得到了不同位置处的爆炸波时程曲线。图5 为实验靶体及传感器布置示意图,装药位于靶体中心位置,圆柱形靶体直径和厚度均为1.83 m,周向设有钢箍,采用不同类型的压力传感器(Yb、PVDF 和Carbon)并设置平行实验,确保实验数据的可靠性。
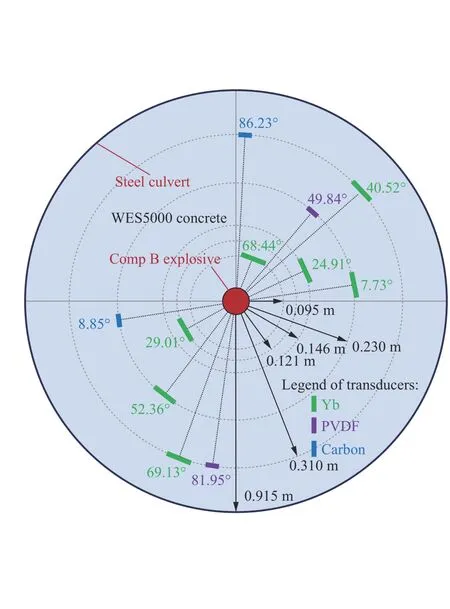
图5 实验示意图[2]Fig. 5 Schematic diagram of the experiment[2]
采用LS-DYNA 中的多物质ALE 算法对实验进行模拟,其中炸药和混凝土均采用ALE 网格,钢箍采用Lagrange 网格,利用流固耦合建立流体ALE 域和Lagrange 域的相互作用。因几何轴对称性,可采用二维轴对称方式建模,如图6 所示。
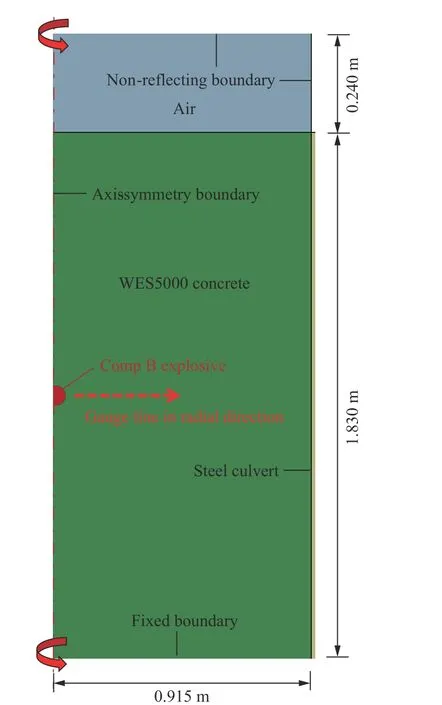
图6 实验的有限元模型Fig. 6 The finite element model for the experiment
选择合适的网格尺寸,可有效提高计算精度和效率,利用上述有限元模型对网格收敛性进行分析。图7 为不同网格尺寸时距装药中心0.15、0.30 和0.5 m 处混凝土中的压力曲线。当网格尺寸小于6 mm 时,压力曲线均收敛,所以,后续数值模拟中网格尺寸均选为6 mm。
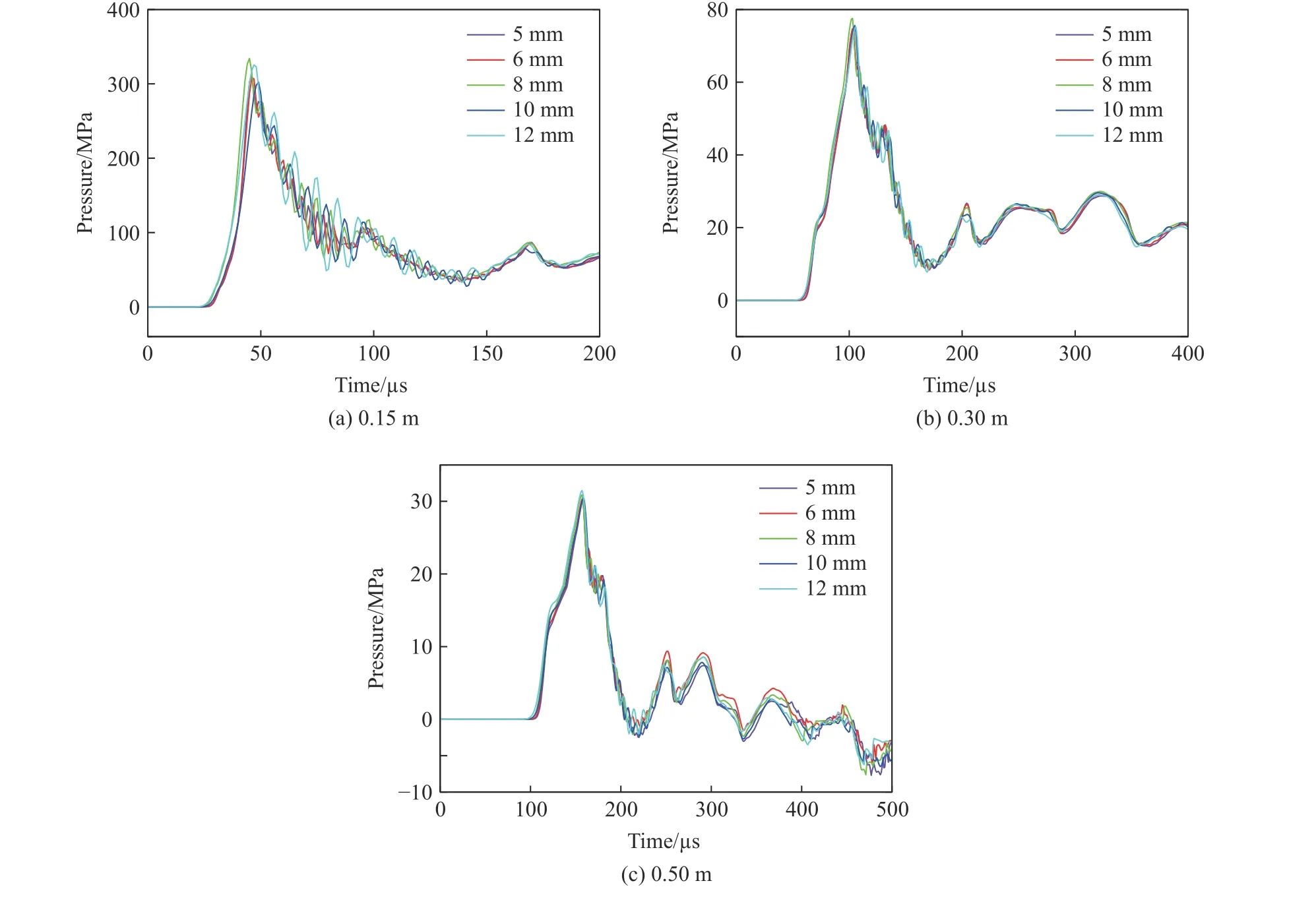
图7 不同网格尺寸的压力曲线Fig. 7 Pressure curves under different mesh sizes
1.3 数值模拟结果验证
现在,利用Gran 等[2]的实验数据验证数值模型结果。
图8 为爆炸波峰值应力随距离的变化,可见数值模拟结果与实验数据良好吻合。进一步,图9 为5 个距离处的应力曲线,可见数值模拟的爆炸波峰值应力、升压时间和正压持续时间均与实验数据较好吻合。这验证了Kong-Fang 混凝土材料模型和多物质ALE 算法的可靠性。
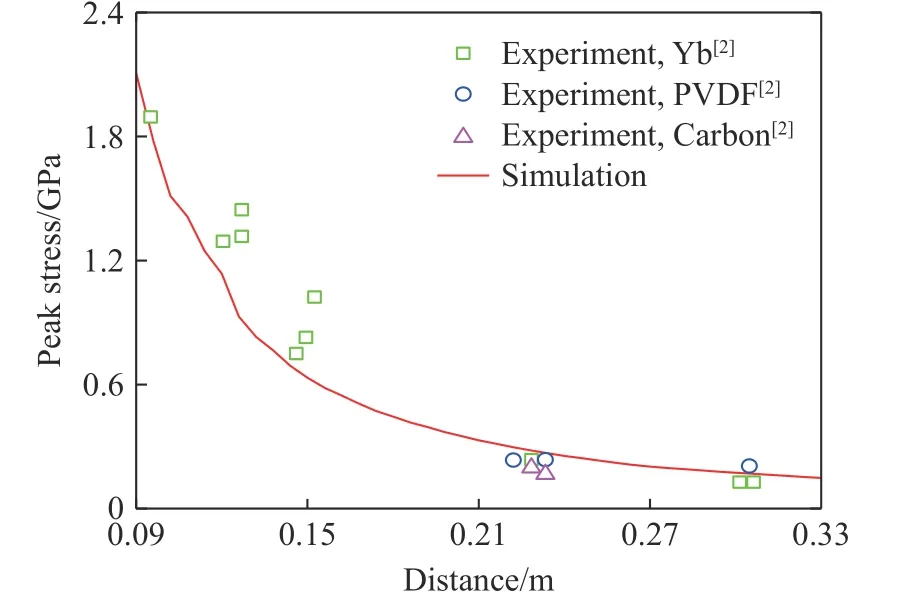
图8 爆炸波峰值应力随距离的变化Fig. 8 Variation of explosion wave peak stress with distances
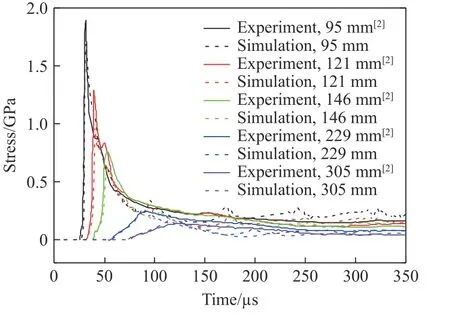
图9 不同距离处的应力曲线Fig. 9 Stress curves at different distances
2 球形装药在混凝土自由场中爆炸波衰减规律
基于上述验证的数值模型,开展球形装药在混凝土自由场中爆炸波衰减规律的数值模拟研究。为便于分析,装药采用1 kg TNT,靶体仍采用WES5000 混凝土,同时为模拟自由场爆炸条件,靶体外边界采用透射边界,有限元模型与图6 相似。
2.1 爆炸波衰减机理
图10 为比例距离0.06~0.20 m/kg1/3混凝土中的径向应力和环向应力曲线。在传播过程中爆炸波迅速衰减,比例距离较小时峰值应力近似呈线性衰减,随着比例距离的增大,衰减速率逐渐变缓,总体呈指数衰减趋势。比例距离小于0.1 m/kg1/3时,为强间断冲击波,上升沿短、脉宽窄,随着传播距离的增加,上升沿逐渐拉长,脉宽逐渐增大,强间断渐变为弱间断。这主要由球面爆炸波自身的扩散效应和混凝土介质对爆炸波的耗散作用共同导致。比例距离为0.06 m/kg1/3时,径向应力和环向应力曲线基本一致,这是因爆炸近区材料剪切强度相对静水压力较小,其力学行为与流体相似;随着比例距离的增大和爆炸波的迅速衰减,混凝土的强度效应逐渐呈现,径向应力和环向应力的差异逐渐显著。依据van Amelsfort 等[28]和TU 等[7]的实验结果和理论预测模型,WES5000 混凝土的压碎强度范围为0.6~1.5 GPa,峰值应力在此范围时混凝土被完全压碎而形成压碎区,强度大于1.5 GPa 时混凝土为近似流体区。利用数值模拟计算的压缩损伤如图11 所示,近似流体区和压碎区的比例半径范围分别为0.08~0.12 和0.12~0.20 m/kg1/3,爆炸空腔的比例半径小于0.08 m/kg1/3。
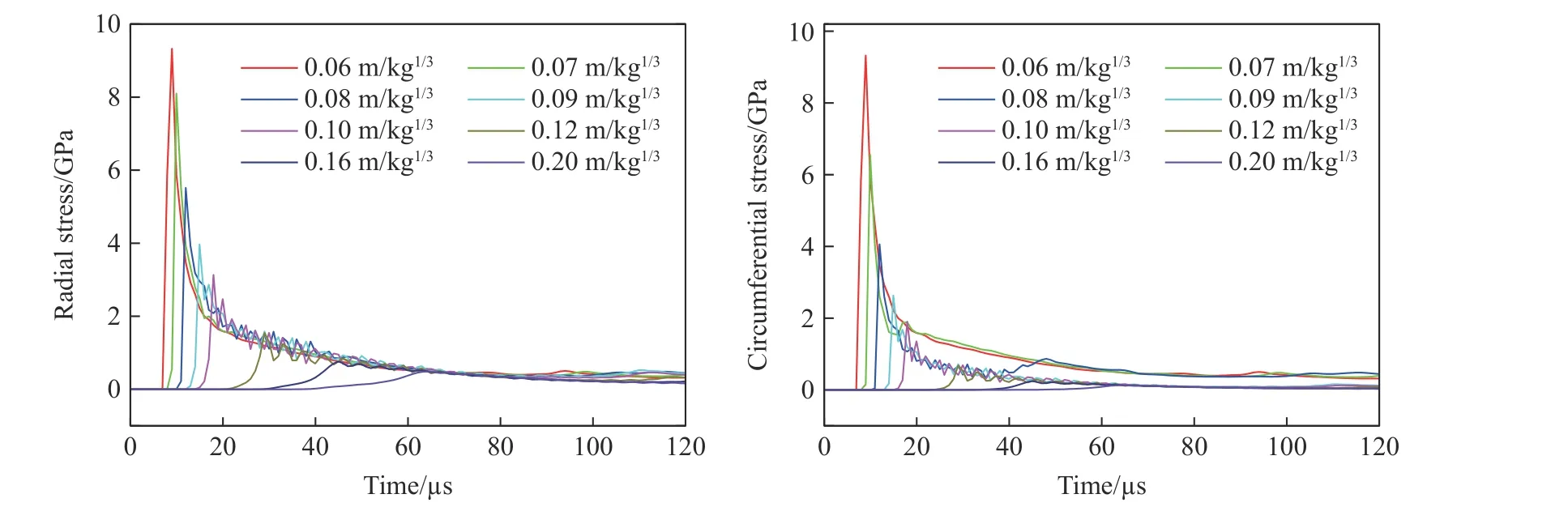
图10 比例距离0.06~0.20 m/kg1/3 时的应力曲线Fig. 10 Stress curves at the scaled distances 0.06-0.20 m/kg1/3
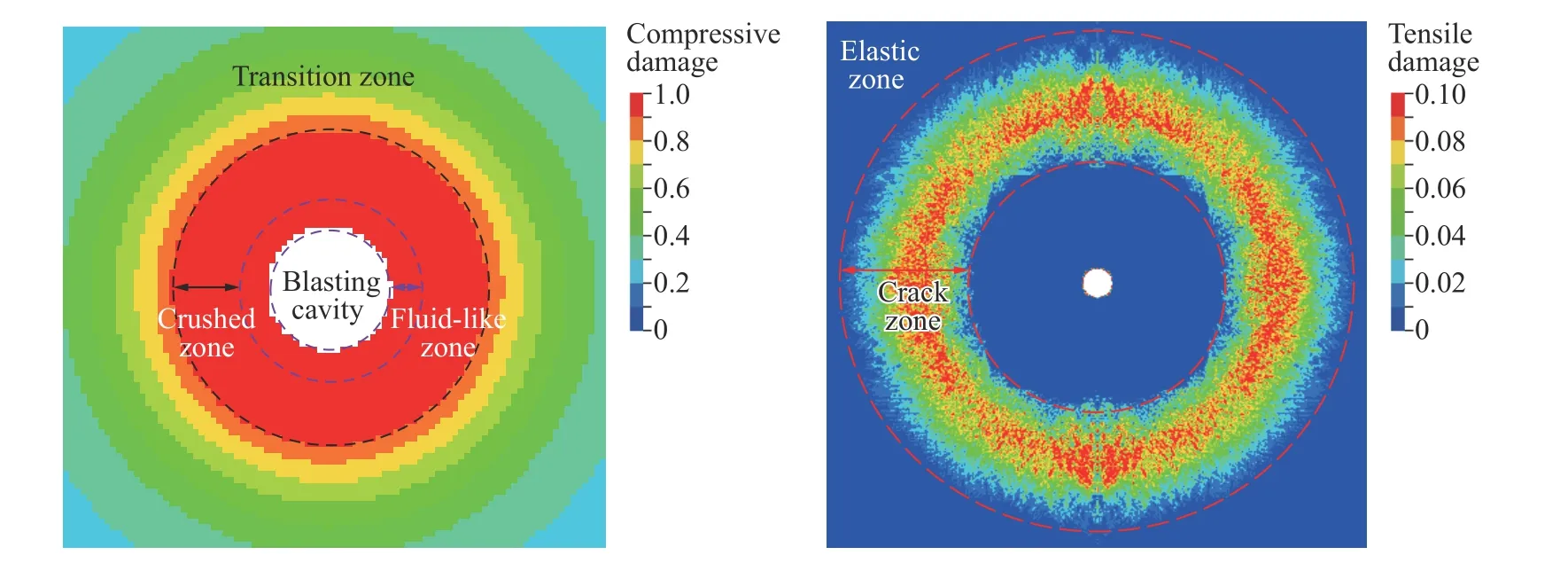
图11 WES5000 混凝土靶体损伤的数值模拟结果Fig. 11 Simulation results for WES5000 concrete target damage
比例距离为0.25~0.60 m/kg1/3时,在混凝土中传播的爆炸波球面除幅值衰减和耗散,还呈现了其他典型特征,如图12 所示。一方面,在塑性峰值应力到达前可观测到明显的弹性前驱波,因弹性前驱波波速高于后续的塑性波波速,随传播距离的增加其波阵面趋于平缓;区别于一维弹性波,因球面波自身的扩散效应,弹性前驱波的峰值应力随传播距离增加而逐渐减小(见图12 中的黑色虚线)。另一方面,各应力曲线出现振荡,峰值后应力不再单调递减,而类似于脉动应力。该现象是因为,爆轰波在混凝土中产生强冲击波的同时,在爆轰产物中形成反向压缩波向爆心传播,压缩波受到产物后方稀疏波的迎面稀疏作用强度不断下降,直至中心汇聚后才重新加载[29-30]。因此,在爆炸过程结束前,爆轰产物内始终存在压缩波及稀疏波的传播及其相互作用,而引起混凝土中爆炸波形的振荡。需要指出,在相关实验[2,4-5]中的应力曲线并未体现波形振荡现象,这可能是因为,波形振荡和传感器噪声引起的振荡无法有效区分,在滤波时被一并滤掉。
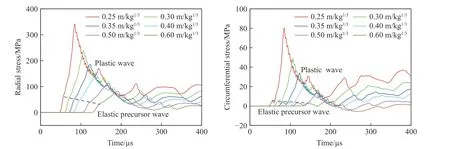
图12 比例距离0.25~0.60 m/kg1/3 时的应力曲线Fig. 12 Stress curves at the scaled distances 0.25-0.60 m/kg1/3
如图13 所示,比例距离继续增加,当比例距离大于1.00 m/kg1/3时,径向峰值应力已低于混凝土的静态抗压强度(41.4 MPa)。同时,到达一定比例距离时,混凝土环向拉伸应力开始主导,这是因混凝土介质在球面压缩波的作用下径向运动时,其环向受到拉应力的作用,且当环向拉应力超过混凝土动态拉伸强度时产生径向裂缝。由于混凝土的抗拉强度远小于抗压强度,因此在压碎区外出现以产生裂缝为主的破裂区[16],且由于裂缝端部的应力集中效应,裂缝可扩大延伸到较远处。采用数值模拟得到拉伸损伤的破裂区如图11(b)所示,其破裂区比例半径为0.7~1.4 m/kg1/3,远大于压碎区的;介于压碎区和破裂区的区域称为过渡区[16],其区域比例半径为0.2~0.7 m/kg1/3。而当混凝土的抗拉强度大于环向拉应力时,不再形成裂缝,混凝土只发生弹性变形,对应的区域称为弹性区。
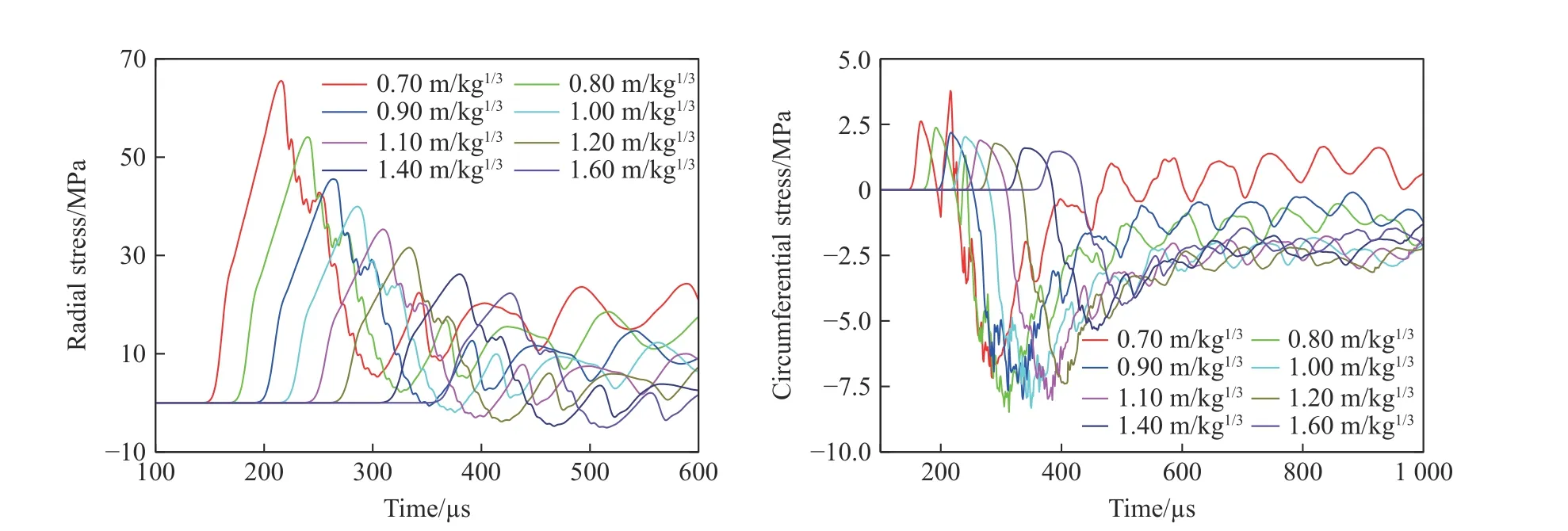
图13 比例距离0.70~1.60 m/kg1/3 时的应力曲线Fig. 13 Stress curves at the scaled distances 0.70-1.60 m/kg1/3
郑哲敏等[31]的流体弹塑性模型中,将爆炸作用下介质的流体、固体特性及运动规律用统一的方程表述。依据该模型并结合上述分析,可将爆炸空腔周围混凝土介质的变形划分为近似流体区、压碎区、过渡区、破裂区和弹性区等5 个区域,如图14 所示。
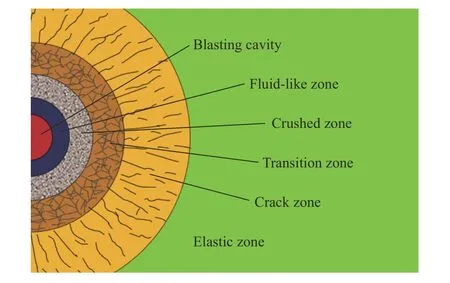
图14 爆炸空腔周围混凝土介质的变形区域Fig. 14 Deformation zones of concrete around the blasting cavity
2.2 量纲分析
爆炸波是混凝土防护结构的主要荷载,对爆炸波峰值等荷载参数的准确预测是确保结构抗爆设计可靠性的前提。借助量纲分析得到混凝土中爆炸效应参数的一般变化规律[32],再结合实验数据和数值模拟,建立混凝土中爆炸波峰值的预测模型。
如忽略混凝土靶体的尺寸效应和爆炸波的耗散,爆炸波峰值等爆炸效应参数X是爆炸能量E、测点与装药中心的距离S、混凝土密度ρ 和混凝土波速ϲ的函数[4,20]。即:

令无量纲量 π1=S(ρc2/E)1/3,则式(3)可变为无量纲函数形式:
中弹的鬼子坚持了几秒,身子一歪,瘫倒在一架鹿砦上,刀枪都脱了手,滚落到一边。他瞪着一只空洞的眼看见余晖落日。

本文中,关注的是峰值应力σ,令无量纲量 π =σ/(ρc2) ,则式(4)变为:

炸药能量E与质量Q成正比,为简化且体现Hopkinson-Cranz 相似律[20,33],用Q替代E,则:

2.3 峰值应力计算公式
由2.1 节,当比例距离大于1.00 m/kg1/3时,爆炸波已衰减为球面弹性波,本文中重点关注比例距离0.09~1.00 m/kg1/3混凝土中的爆炸波峰值应力分布。在此比例距离,爆炸波为塑性波,c应取塑性波速。
WES5000 混凝土的密度ρ=2 180 kg/m3,可通过图10、12 中爆炸波峰值应力达到时间和距离得到塑性波速c=3 200 m/s。由此,可建立无量纲峰值应力 σ*与距离S*的关系,如图15 所示。可见, σ*与S*呈指数关系:
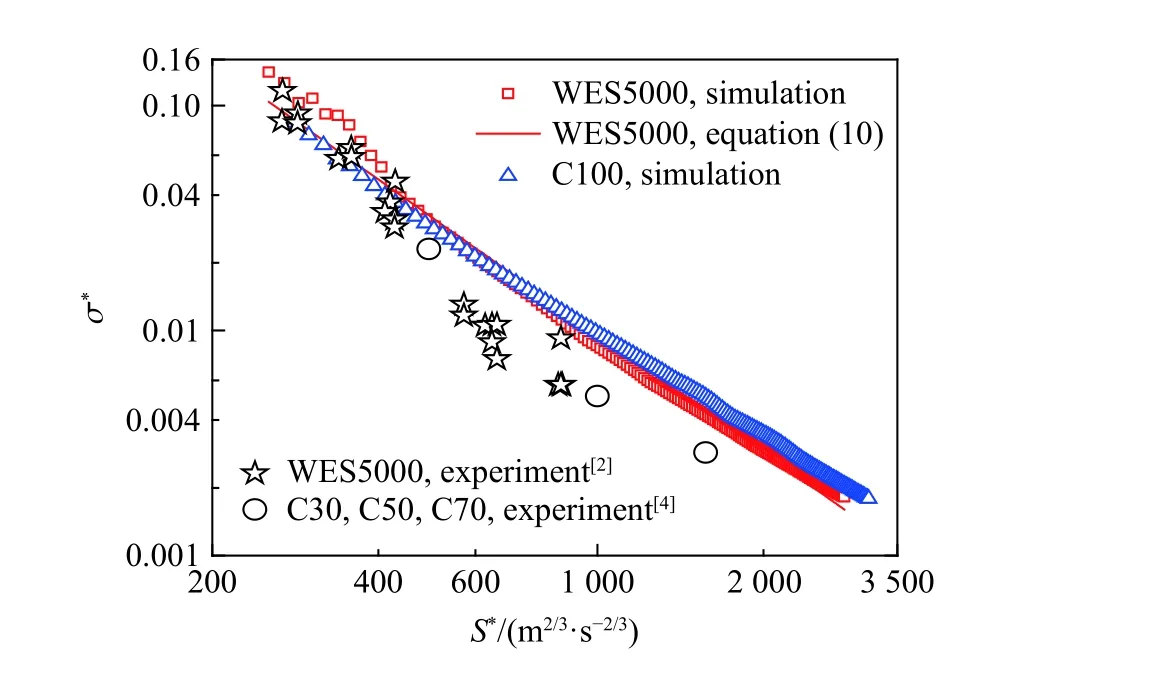
图15 爆炸波峰值应力随距离的变化Fig. 15 Variations of explosion wave peak stress with distance
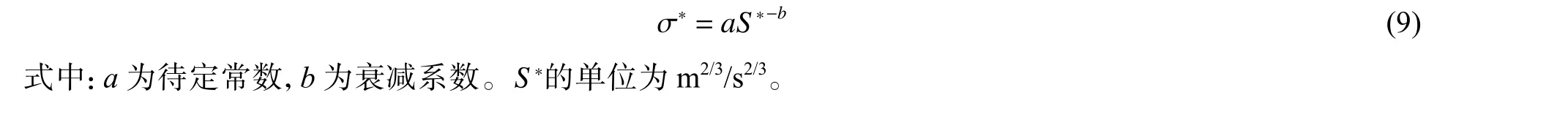
基于2.1 节数值模拟的混凝土自由场中爆炸波峰值应力数据,可拟合得到a=1 525,b=1.734,相关系数R2=0.977。由此,可建立WES5000 混凝土自由场中爆炸波峰值应力的计算公式:

由量纲分析结果,爆炸波峰值应力与混凝土密度和波速(波阻抗)密切相关。为验证式 (10)在其他强度混凝土中的适用性,建立1 kg 球形TNT 装药在C100 混凝土自由场中爆炸的数值模型,并根据实验数据和数值模拟结果,得到C100 混凝土密度ρ=2 570 kg/m3、塑性波波速c=3 434 m/s。图15 为式(10)与数值模拟结果的比较,可见式(10)可较好地预测数值模拟的 σ*和S*的关系。
为进一步验证式(10)的可靠性和适用性,与Gran 等[2]和Mu 等[4]不同强度混凝土中的爆炸波峰值应力实验数据比较,在整体上式(10)较好吻合。Mu 等[4]根据实验数据,确定了不同强度混凝土的衰减系数b=1.67~1.84,而式(10)中衰减系数b=1.734,与之吻合。
3 装药埋深对峰值应力分布的影响
式(10)中仅适用于装药在混凝土完全内爆(自由场)情况,事实上,武器弹药命中目标时的埋深常介于接触爆炸和完全内爆之间,本节中将分析装药埋深对混凝土中爆炸波峰值应力分布的影响。
3.1 不同装药埋深下爆炸波峰值应力
图16 为1 kg 球形TNT 装药在WES5000 混凝土中不同埋深时,装药正下方无量纲峰值应力σ*与距离S*的关系,其中比例埋深h*为装药中心到靶体上表面的比例距离。可以看出,接触爆炸(h*=-0.053 m/kg1/3)与自由场爆炸在相同距离S*处的 σ*有明显差异,且随着装药埋深的增加差异逐渐减小,当比例埋深大于0.1 m/kg1/3时与自由场爆炸几乎无差异。
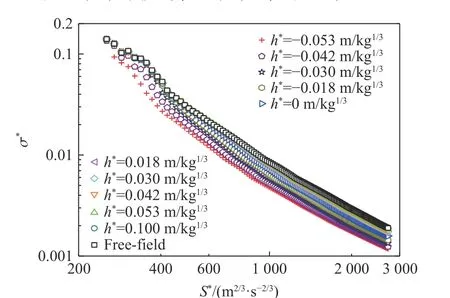
图16 不同埋深时WES5000 混凝土的爆炸波峰值应力随距离的变化Fig. 16 Variations of explosion wave peak stress for WES5000 concrete with distance at different burial depths
3.2 混凝土爆炸波峰值应力耦合系数
目前,变埋深条件下装药爆炸能量和混凝土介质的耦合形式和比例尚无定论[16-17]。在手册TM5-855-1 中,定义耦合系数f为部分埋设或浅埋爆炸与完全埋设爆炸(自由场爆炸)在相同介质中所产生爆炸效应的比[18]。本文中,重点关注装药正下方爆炸波峰值应力随装药埋深的变化,则定义爆炸波峰值应力耦合系数:

第1 阶段:爆轰波直接作用,f=1。

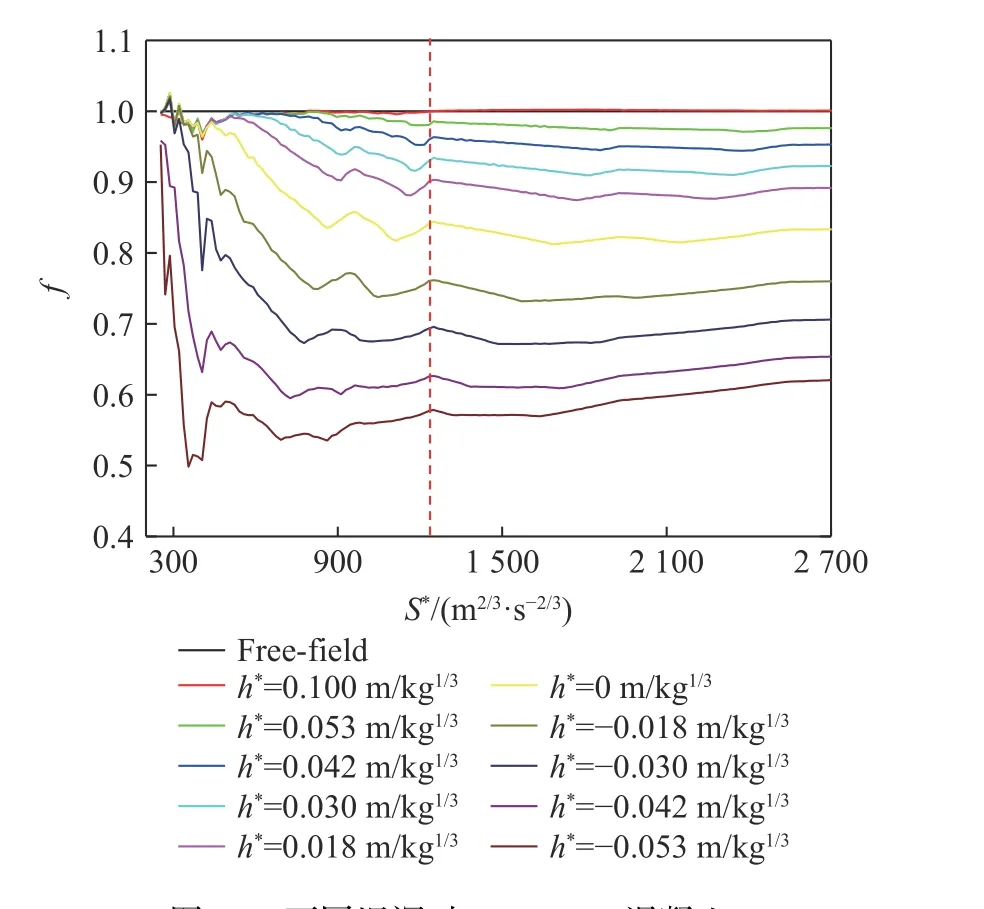
图17 不同埋深时WES5000 混凝土峰值应力耦合系数随距离的变化Fig. 17 Variations of peak stress coupling coefficient for WES5000 concrete with distance at different burial depths
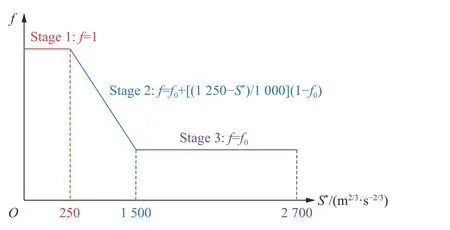
图18 峰值应力耦合系数随距离的变化规律Fig. 18 Variety rule of peak stress coupling coefficient with distance
第3 阶段:冲击波衰减为稳定的弹塑性波,耦合系数几乎不变化,为常数f0。

Mu 等[4]的实验表明,混凝土的爆炸效应耦合系数不仅受装药埋深的影响,还与混凝土材料的强度等指标高度相关。为验证建立的爆炸压缩波峰值应力耦合系数计算公式对其他强度混凝土的适用性,通过数值模拟计算C100 混凝土在接触爆炸( µ*=0)和半埋爆炸( µ*=0.5)时的峰值应力耦合系数(见图20),可见其值与WES5000 混凝土差别不大。由此说明,建立的峰值应力耦合系数计算公式具有广泛的适用性,在已知装药埋深(质量系数 µ*)时,能快速确定离装药中心特定距离S*处混凝土的峰值应力耦合系数。
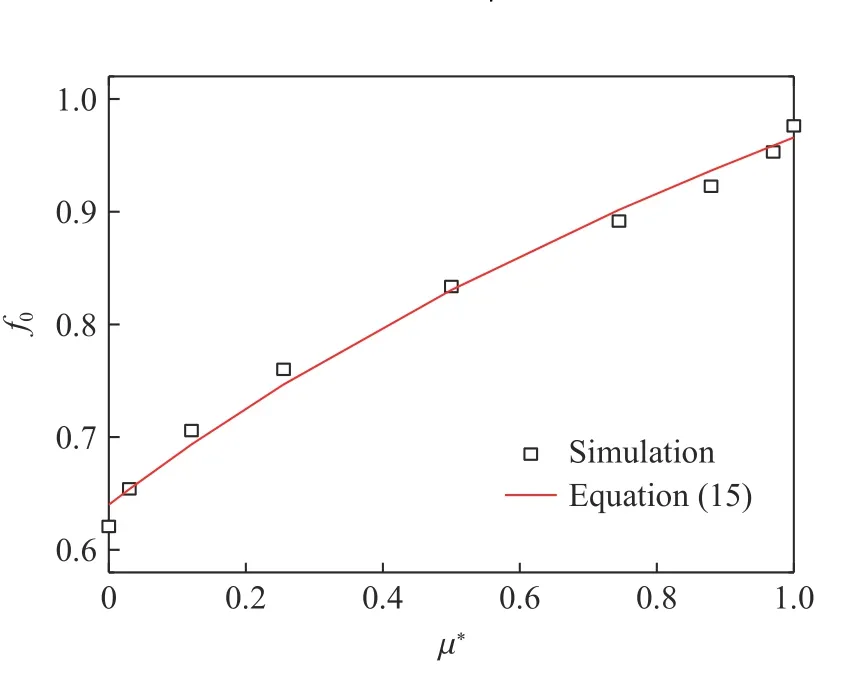
图19 稳定峰值应力耦合系数随质量系数的变化Fig. 19 Variation of stable peak stress coupling coefficient with mass coefficient
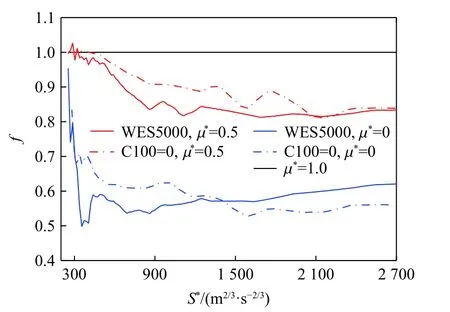
图20 WES5000 和C100 混凝土的峰值应力耦合系数随距离的变化Fig. 20 Variations of peak stress coupling coefficients for WES5000 and C100 concretes with distance
3.3 变埋深条件下爆炸波峰值应力计算公式
由式(16)结合式(10),可得任意装药埋深和测点距离下球形装药正下方混凝土中爆炸波峰值应力的计算公式:

4 结 论
基于Kong-Fang 混凝土材料模型,利用LS-DYNA 中的多物质ALE 算法,开展球形装药在混凝土中爆炸波衰减规律的数值模拟。通过模拟已有实验验证了数值模型的可靠性,在此基础上分析了混凝土自由场中爆炸波衰减规律,并探讨了装药埋深对混凝土中近区爆炸波峰值应力分布的影响。主要结论如下。
(1) Kong-Fang 混凝土材料模型在模拟混凝土中爆炸波传播规律时具有较高精度,可有效预测混凝土中爆炸应力波传播的衰减规律。
(2) 借助量纲分析,利用数值模拟结果建立的球形装药在混凝土中近区爆炸波峰值应力的计算公式具有良好的可靠性和适用性,在已知混凝土密度、 塑性波波速和装药量下,能快速预测特定距离下混凝土中爆炸波峰值应力。
(3) 耦合系数不仅与装药埋深有关,还与测点与装药中心的距离有关;建立了爆炸波峰值应力耦合系数与装药在混凝土中的质量系数、与装药中心距离的定量关系,可较准确地计算任意埋深条件下球形装药正下方混凝土中特定距离处的爆炸波峰值应力。
