非均质床垫硬度测试的方法及改进

刘 美, 申黎明, 卢 涛, 房娇娇

(1. 南京林业大学 家居与工业设计学院, 江苏 南京 210037; 2. 南京金榜麒麟家居股份有限公司, 江苏 南京 210032)

1 引 言

床垫的固有非均质性决定了床垫复杂的受力变形过程,使得床垫的硬度测试也随之变得不易。即使相关标准规定了床垫硬度的测试方法,一些研究仍使用软、中、硬等模糊词语来区分床垫硬度[1～10]。一方面,是因为使用主观评价法来描述床垫硬度，可以对床垫进行快速分类;另一方面,是因为不同标准的测试方法和结果是不同的,且未见对这些标准进行分析和比较的研究报道。

目前关于床垫硬度测试的标准和研究主要有:ISO 2349/B MOD I (简称CTBA测试方法),这种方法是较细致的1种测试方法。主要针对床垫的非均质性,通过分层测试反映床垫的表层、中层和底层硬度, 每1层的位移值即为该层硬度值，只侧重于测算床垫各分层的软硬程度,不能对床垫整体的硬度进行综合评价[11,12]。

EN 1957:2012 与QBT 1952.2-2011(简称LGA测试法),这种方法充分考虑了人的主观感受性差异。据此,在床垫加载挠度曲线上取3个特定加载力处的切线斜率,将其平均值作为床垫硬度值。但3点中的最大加载力(F=450 N)对床垫产生的压强远远低于人对床垫所产生的最大体压[13,14]。姜婷婷提出综合刚度测试法,从客观的角度对床垫整体进行了测试。将床垫加载挠度曲线进行线性拟合所得的斜率作为综合刚度系数来度量的床垫硬度。与CTBA测试方法相反,这种方法忽略床垫的非均质性，因此线性拟合效果较差,且拟合范围仍需斟酌[15～22]。同时,这种方法所使用的测试设备、压盘大小和形态不同,测试结果也有所不同。

为此,本研究使用特制设备量取了床垫加载挠度曲线,借鉴CTBA测试方法、LGA测试法和综合刚度测试法的测试原理,针对使用较广泛的LGA测试法提出了3种优化方法,以寻找一种更周全的床垫硬度测试方法,为床垫硬度测试提供可靠的理论依据和测试方法。

2 床垫硬度测量实验

2.1 实验目的

实验共设置2组实验床垫:弹簧床垫组和海绵床垫组,并假设这2组实验床垫因弹性材料的不同导致2组间的硬度有明显差异,即2组间的硬度差异大于每组内的硬度差异。通过测量床垫在一定加载力下的位移值,获得床垫加载挠度曲线,分别使用LGA测试法和3种优化方法对床垫硬度进行测试,根据测试结果的相互对比来确定LGA测试法和3种优化方法的优劣,从而找出较适合测试床垫硬度的方法。

2.2 实验床垫

实验共16款非分区床垫,其中8款是弹簧床垫(spring mattress,SM),芯层为袋装圆柱弹簧,铺垫层有绵羊毛毡、慢回弹海绵、乳胶海绵和普通海绵等,复合面料层为针织面料绗缝普通海绵、丝绵和无纺布组成,弹簧床垫材料配置如表1所示。

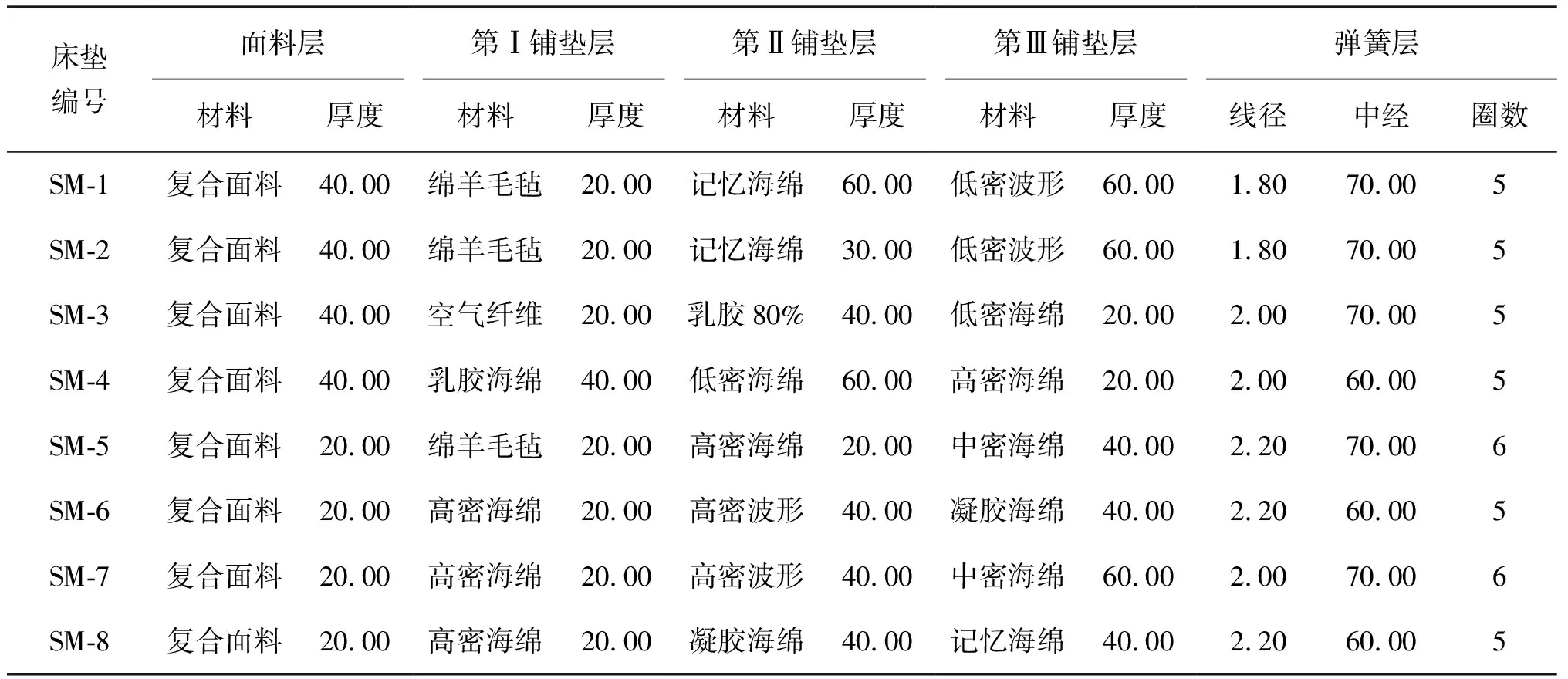
表1 弹簧床垫配置表Tab. Spring mattress configuration table mm

另外8款是海绵床垫(foam mattress,FM),主要使用绵羊毛毡、慢回弹海绵、乳胶海绵和普通海绵等,复合面料层同弹簧床垫一致。海绵床垫铺垫层材料配置如表2所示,海绵床垫面料层为复合面料,厚度20.00 mm;支撑层为高密海绵,80.00 mm。

2.3 实验方法

实验使用MCK-Z-I型智能测试仪(示意图如图1所示)测量实验床垫的加载挠度曲线,该测试仪有3个压盘,分别对床垫不同部位(上部、中部和下部)进行测试。实验在南京林业大学人体工程学研究所进行,控制室温为(23±2)℃、相对湿度为(50±5)%。实验前,将床垫放置在实验台上,调节压盘的位置使中间压盘刚好位于床垫正中位置,两端的压盘与中间压盘间距500 mm。实验时,先将3个压盘调节至床垫表面后,然后均匀施加压力,测得床垫加载挠度曲线,测量3次后,对0,10,20,30,40,50,60,70,80,90,100,110 N处共12个散点进行研究。

表2 海绵床垫配置表Tab.2 Foam mattress configuration mm

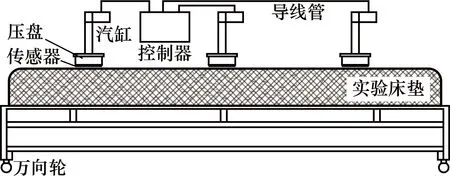
图1 MCK-Z-I型智能测试仪示意图Fig.1 Schematic diagram of MCK-Z-I intelligent display controller

2.3 床垫硬度测试方法

2.3.1 加载力阈值确定

LGA测试使用设备的压头直径为355 mm,衔接半径为800 mm的凸出球面。在测试时,加载力会迅速向四周分散开,使得整个球面均匀受力。与平面相比,球面对床垫的施力更小,若以平面进行测试,最大加载力F为450 N对床垫产生的的压强为:

因此，球面压头对床垫施加的压强小于4.546 kPa,而床垫硬度测试的最大加载力应大于人体在床垫上所产生的的最大体压。当人体采用仰卧睡姿时,臀部会产生最大的压强;采用侧卧睡姿时,肩部会产生最大的压强。同时,最大压强会受被试者的胖瘦程度、性别以及床垫硬度等因素的影响,一般身体质量指数(BMI)较大的男性被试者在硬床垫上会产生较大的压强。因此,挑选了1名男性国家二级举重运动员作为被试者进行体压采集,该被试者身高173 cm、体重101.5 kg、BMI为33.9。实验时,分别采用仰卧和侧卧2种睡姿在软床垫和硬床垫上进行试躺,并对其臀部和肩部的体压进行采集,共获取8张体压图,如图2所示。

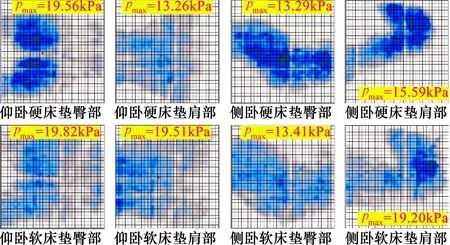
图2 被试者在软、硬床垫上臀部和肩部的体压分布Fig.2 Participants′ body pressure distribution on the hips and shoulders on soft and hard mattresses

由图2可知,该被试者侧卧在硬床垫上时,臀部产生最大体压为19.82 kPa。实验所使用的压盘直径为80 mm,因此,测试所需的最大加载力应F≥Fs,Fs=(80 mm/2)2×19.82 kPa=99.63 N。因此,将测试的最大加载力加以修正至110 N。

2.3.2 LGA测试方法

利用k次B样条将床垫加载挠度曲线拟合成函数。k次B样条曲线的表达式为:

式中:i为B样条基函数的序号,i=0,1,…,n;Ni,k(u)为k次B样条基函数;Vi为控制顶点向量。k次B样条基函数由de Boor Cox递推公式得到:

式中: B样条基函数的次数k=3,将12个散点(x0,x1,…,x11)划分为11段分别进行拟合,得到:

图3 LGA测试法的计算原理图Fig.3 Calculation principle diagram of LGA test method

如图3所示,分别取床垫加载挠度曲线上3点处的切线斜率进行计算,床垫硬度值为切线C1、C2、C3斜率的平均值。即

当C1、C2、C3不同时,实验所测得的硬度值将发生变化,C1、C2、C3在不同点处测得的弹簧床垫硬度值如表3所示。

表3弹簧床垫在不同加载力下的硬度值对比Tab.3 Comparison of stiffness values of spring mattresses under different loading forces mm

海床垫硬度值如表4所示。

由表3和表4可知,随着加载力的增大,床垫硬度值逐渐增大。从表3可知,30-50-70、30-60-90和20-60-100所测得的数据较为接近(30-50-70表示C1为30 N处的切线,C2为50 N处的切线,C3为70 N处的切线等),在加载挠度曲线上均匀分布。其中,20-60-100的加载力间距最大,分别位于床垫表层、中层和底层,是较合适的间距。因此,LGA测试法实验时选择的3点处加载力分别是20,60,100 N。

2.3.3 测试优化方法

1) 优化方法1

针对LGA测试法的不足,优化方法1增加了测试点数,如图4所示。

将10,20,30,40,50,60,70,80,90,100,110 N处的切线分别记作C1,C2,C3, …,C11, 床垫硬度值为切线C1,C2,C3, …,C11斜率的平均值:

利用这种方法,对实验弹簧和海绵床垫进行测试,结果如表5所示。

表4 海绵床垫在不同加载力下的硬度值对比Tab.4 Comparison of stiffness values of foam mattresses under different loading forces mm

图4 优化方法1的计算原理图Fig.4 Calculation principle diagram of optimization method 1

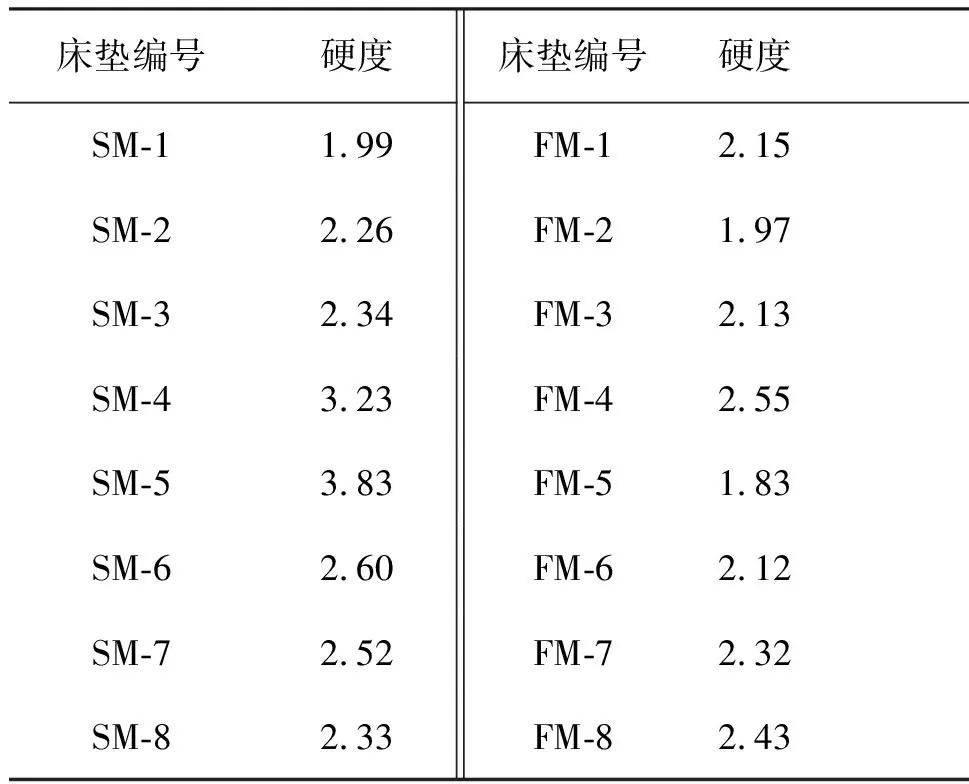
表5 利用优化方法1计算所得弹簧和海绵床垫硬度值Tab.5 Use optimization method 1 to calculate the hardness value of spring and foam mattress mm

2) 优化方法2

在一定加载力范围内,加载力F与下陷量H之间呈线性关系,其线性拟合的斜率可以作为综合刚度系数来度量床垫的硬度,如图5所示[19]。本研究在此基础上,分别在0～110, 10～110, 20～110及30～110 N四个加载力范围内进行线性拟合，拟合方程为:

y=kx+b

图5 优化方法2的计算原理图Fig.5 Calculation principle diagram of optimization method 2

拟合结果如表6和表7所示。随着范围的缩小,相关系数R2逐渐增大,初始下陷量逐渐增加,所测得的硬度值也逐渐变大。当范围为20～110 N时,有15款实验床垫的R2已达0.97,加载力与下陷量之间线性关系非常强。当范围为30～110 N时,有15款实验床垫的R2达到0.98,这种线性关系更加强烈,但这时初始下陷量过大,使得30～110 N的下陷量不足床垫总下陷量的一半。因此,20～110 N是较好的计算范围。

表6利用优化方法2计算所得弹簧床垫的硬度值Tab. Use optimization method 2 to calculate the hardness value of spring mattress mm

表7利用优化方法2计算所得海绵床垫的硬度值Tab.7 Use optimization method 2 to calculate the hardness value of foam mattress mm

3) 优化方法3

对于已经作用于床垫上的力F, 因位移dΔl而做功dW=F·dΔl, 也就是阴影部分的面积,如图6所示。

力F做功使床垫储备了一定的能量,忽略加载力缓慢移动带来的动能,主要是势能。床垫硬度与势能之间存在正相关关系,对床垫势能的测试可以反映床垫的硬度。因此,在0～110 N的加载力范围内,利用势能求得加载力与下陷量之间的比例系数可以作为物理参量来度量的床垫硬度值。使用梯形法,将一个区域分为包含多个更容易计算的梯形区间进行近似积分计算,得到加载挠度曲线与x轴之间的面积,即床垫势能,如图6所示。

图6 优化方法3的计算原理图Fig.6 Calculation principle diagram of optimization method 3

对于具有N+1个均匀分布的点的积分,近似值为:

由于各测量点之间的下陷间距并非定值,即各N+1点之间的间距不是常量,则:

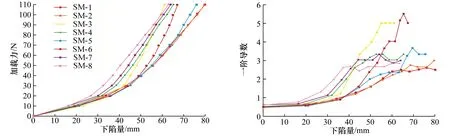
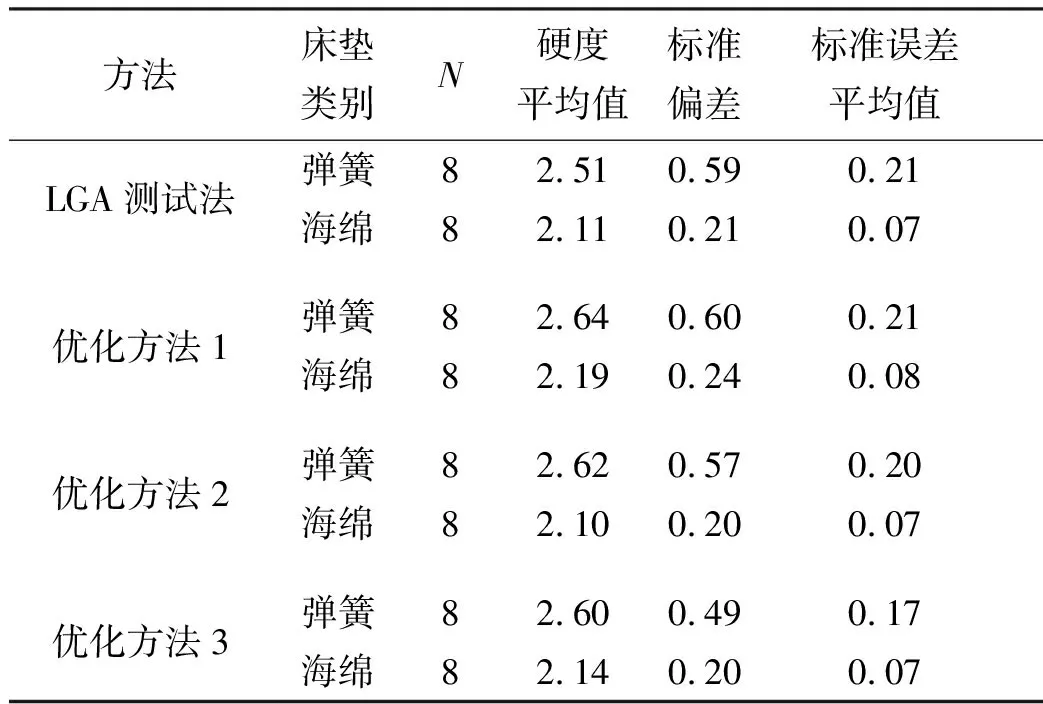
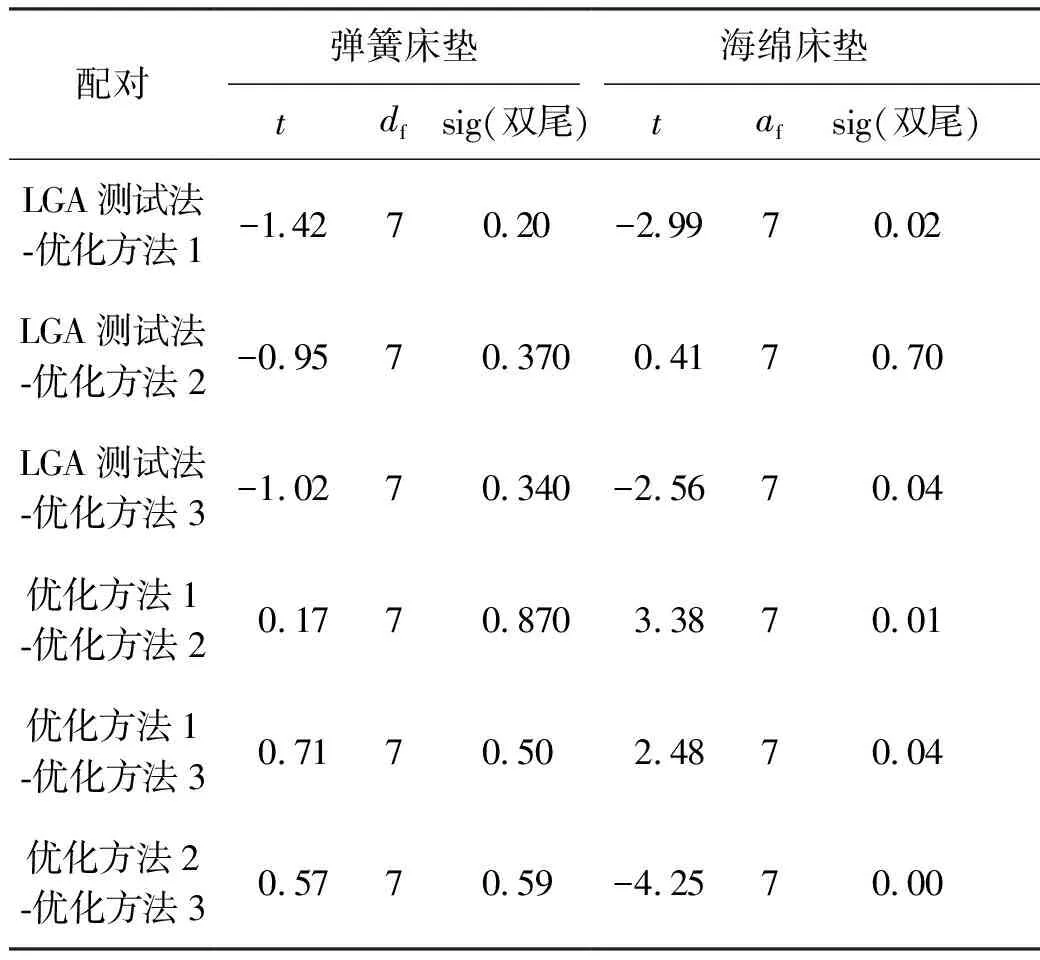
式中0=x1

曲线共经过n个点(xi,yi),i=1,2,…,n。曲线下的面积S为:

表8优化方法3计算所得弹簧和海绵床垫的硬度值Tab.8 Optimization method 3 to calculate the hardness value of spring and foam mattress mm

3 结果与分析

3.1 实验结果

分别利用LGA测试法及其3种优化方法对弹簧床垫和海绵床垫的测试结果如表9所示。由表9可知,4种方法所测算的实验床垫硬度值略有差异。

从16款床垫的加载挠度曲线来看,弹簧床垫与海绵床垫存在较大的区别,弹簧床垫下陷量的增加,床垫硬度增值存在明显转折,硬度分层明显。但海绵床垫硬度随着下陷量的增加均匀递增,没有硬度分层。且从导数曲线来看,弹簧床垫硬度呈现先增加后逐渐平稳的趋势,而海绵床垫硬度在持续增加,如图7和图8所示。由此可见,正如假设,弹簧床垫和海绵床垫具有较大差异。

表9 利用LGA测试法和3种优化方法计算所得弹簧床垫和海绵床垫的硬度值Tab.9 Using LGA test method and 3 optimization methods to calculate the hardness value of the spring and foam mattress mm

图7 弹簧床垫加载挠度曲线及其一阶导数曲线Fig.7 The spring mattress loads the deflection curve and its first-order derivative curve

图8 海绵床垫加载挠度曲线及其一阶导数曲线Fig.8 The foam mattress loads the deflection curve and its first-order derivative curve

3.2 组间独立样本t检验

3.2.1 均值分析

利用SPSS对LGA测试法及其优化方法进行均值分析,结果如表10所示。

由表10可知,3种优化方法对弹簧床垫测算的平均值在(2.62±0.2) mm内,比LGA法测算的结果大0.1 mm。但是,4种方法对海绵床垫测算的平均值在(2.14±0.05) mm内。

表10利用LGA测试法和优化方法1测的2组床垫间差异

3.2.2 样本t检验

利用SPSS对LGA测试法及其优化方法进行独立样本t检验,如表11所示。

由表11可知:LGA测试法方差齐性F检验的F=5.63,sig=0.03<0.05,即为非齐性方差,此时P(sig)=0.10>0.05,2组数据无显著差异;优化方法1方差齐性检验的F=3.62,Sig=0.08>0.05,即为齐性方差,此时P=0.07>0.05,两组数据无显著差异; 优化方法2方差齐性检验的F=4.29, sig=0.06>0.05,即为齐性方差,此时P=0.03<0.05,2组数据有显著差异;优化方法3方差齐性检验的F=3.23, sig=0.09>0.05,即为齐性方差,此时P=0.03<0.05, 2组数据有显著差异。由此可见,LGA测试法和优化方法1与假设不符,而优化方法2和3与假设一致。

表11利用LGA测试法和优化方法1所测的组独立样本检验Tab.11 Use the LGA test method and the optimized method 1 to test the independent sample of the tested group mm

3.3 组内配对t检验分析

利用LGA测试法及其优化方法对弹簧床垫组和海绵床垫组进行配对样本t检验,如表12所示。结果显示:在弹簧床垫组内,6个配对的P(sig值)>0.05,4种方法间的差异无统计学意义;在海绵床垫组内,配对2的P(sig值) =0.70>0.05,LGA测试法与优化方法2的差异无统计学意义,此外5个配对的P值<0.05,差异具有统计学意义,如表12所示。由此可见,4种方法对弹簧床垫的测算没有差异,但对海绵床垫的测算除了LGA测试法与优化方法2没有差异外,4种方法在0.05显著性水平下存在差异。

表12优化前后弹簧床垫和海绵床垫的配对样本t检验Tab.12 Optimized the paired sample t test of spring mattress and foam mattress before and after optimization mm

4 结 论

针对使用较广泛的LGA法床垫硬度测试方法,提出了3种优化方法。经过组间和组内t检验得出以下结论:

1) 针对本研究所使用的设备,较适合LGA测试法的3点处加载力分别是20, 60, 100 N,较适合优化方法2的加载力范围是20～110 N,但这2种方法对床垫硬度的测试基于人为规定,且受测试设备(如压盘半径、形状等)的影响,不是理想的测试方法;

2) 由组间对比结果可知,优化方法2和3显示弹簧组和海绵组的组间存在显著性差异,与假设相符;

3) 由组内对比结果可知,在弹簧床垫组内,4种方法无显著性差异;在海绵床垫组内,优化方法1和3与LGA测试法在0.05显著性水平下存在差异,且3种优化方法彼此之间均存在显著性差异,但优化方法2与LGA测试法无显著性差异;

4) 由此可以看出,4种方法中,LGA测试法和优化方法2不具有唯一性,且受到测试设备的影响。在组间对比时,LGA测试法和优化方法1显示弹簧组和海绵组无显著性差异,与假设不符。方法3与其他3种方法不具有显著性差异,且对床垫硬度值的测算具有唯一性,不受测试设备的影响,对组间差异的测算与假设相符。因此,优化方法3是较为理想的床垫硬度测试方法。