基于协克里金的雨量雷达融合置信处理方法

陈根华，莫正威

(南昌工程学院 信息工程学院，江西 南昌 330099)

降雨量是降雨型灾害预警与降雨径流模型研究的关键信息。目前，较广泛运用的降雨测量仪器包括雨量雷达、雨量计和气象卫星等，利用采集的雨量相关数据，结合数据分析能力形成数字化天气预报模型[1]。本文分析雨量雷达和雨量计两类仪器在降雨测量中的融合利用。

雨量计提供较为准确的降雨测量数据[2]。但只能提供局部点数据测量，区域雨量的2-D形成需要使用插值技术。受限于陡峭地形、宽广水域及布设成本，高密度雨量计站网难以建立，造成降雨测量的时间与空间分辨率较低，极易导致“测不到”问题[3]，降低了区域降雨测量性能，在强对流天气下尤为明显，观测时易漏掉强降雨中心。而雨量雷达依靠其高时空分辨率，可实现区域雨量的无缝测量，提供区域降雨空间变异性的准确描述，在降雨估测中被广泛应用[4]。雨量雷达采用电磁波反射理论，通过建立反射率因子与降雨量之间的函数关系，实现区域降雨估计，但由于地物回波、超折射回波、零度亮层[5]以及雷达元器件等影响，在定量降水估计(Quantitative Precipitation Estimation，QPE)方面的准确度低于雨量计[6]，形成“测不准”现象[4]。常用的QPE方法有反距离加权法[7]、双调和样条插值法[8]、基于三角剖分的插值法等[9]，但以雨量计为单一数据来源的方法，因雨量计测量范围小的缺点，难以详细反映区域内降雨的变异性，导致区域估计降雨情况与实际情况产生偏差，甚至漏掉强降雨中心等。

本文结合数据融合技术，提出了雨量雷达数据融合置信处理算法。该算法先对雨量雷达获取的反射率因子(Radar Reflectivity Factor)进行Z-score标准化处理，再以标准化处理后的反射率因子数据为辅变量，雨量计数据为主变量，利用空间变异理论[10]中的协克里金法[11]，实现雨量雷达与雨量计数据的融合置信处理。实现了异质数据的融合，结合两种仪器的良好品质，较好地解决了雨量计“测不到”和雨量雷达“测不准”问题，改善了常规雨量计站网的区域降雨观测能力，提高了雨量雷达定量降水估计的准确度。本文同时定义了雨量雷达降雨估计的相对置信度，并分析了融合处理后雨量雷达降雨估计的相对置信度分布情况。仿真试验结果验证了雨量雷达数据的融合置信处理算法的正确性与有效性，提高了雨量雷达QPE的准确度及测量的稳健性。

1 数据模型

雨量雷达在区域降水探测中，具有探测范围广、时空分辨率高等优势，但探测环境的复杂多变常影响雨量雷达的探测精度，导致俗称的“测不准”现象[4]。气象部门常利用高精度的雨量计作为真实降水量的度量仪器，但测量范围受成本、布设场地等多种因素的制约无法实现高密度测量，出现所谓的“测不到”问题，如图1所示。

图1 雨量雷达工作示意图

雨量雷达通过接收水滴对入射波的反射回波，可计算出散射截面σb，即

σb≈(π5/λ4)|Kω|2D6，

(1)

其中λ是入射波波长；D是水滴直径，且D≤λ/16；Kω=(m2-1)/(m2+2)，m=n-jnκ，m是水的复折射率，n是折射率，κ是衰减指数。

利用雷达气象方程

(2)

反射率因子Z为

(3)

其中N(D)表示单位体积内直径范围在D和D+dD之间水滴粒子的粒子数；Z的单位为mm6/m3。

由于雷达反射率因子Z和降雨量R是雨滴尺寸分布(DSD)的两种不同矩(Moment)形式，因此，Z-R关系可表示为

Z=aRb

(4)

其中系数a的变化范围为16～1200，系数b的变化范围为1～2.8[5]。雷达降水估计的影响因素复杂，包括异常杂波、零度亮层、衰减、风场、温度、湿度等，导致Z-R关系在定量降雨估计方面精度不足。因此，本文提出一种融合置信处理算法，结合雨量雷达和雨量计两种仪器的优势，提高雨量雷达定量降雨估计的准确度。

工程上，雨量雷达数据是以最小分辨单元为基本单位输出雨量数据，包含距离、方位角、反射率、多普勒谱宽等多种探测信息。本文针对反射率因子进行融合处理，因此以雷达为参考中心，以最小分辨单元为基本单位提取反射率因子和位置数据，包括距离r、方位角φ和反射率因子Z，可将雷达数据表示成矢量形式，即D=[r，φ，Z]T，则可得雨量雷达数据集R∈3×N为

R=[D1，D2，…，DN]，

(5)

其中N为雷达分辨单元个数。

同理，雨量计数据包含距离r、方位角φ和降雨量g，表示成矢量形式，即S=[r，φ，g]T，则雨量计数据集G∈3×N为

G=[S1，S2，…，SM]，

(6)

其中M为雨量计站点个数。

显然，雨量雷达分辨单元数N远大于雨量计站点数M，即N≫M。在气象、水文、地质灾害监测等应用中，如何利用少量雨量计提高雨量雷达降雨估计精度具有重要的工程意义。本文拟采用数据融合技术，充分利用雨量雷达和雨量计的良好品质，实现雨雷达和雨量计在数据层[6]的融合，以提高雨量雷达定量降雨估计的精度。

因此，本文提出融合置信处理算子F (·)，对雨量雷达和雨量计数据进行融合置信处理，以提高雨量雷达降雨估计精度，得到区域雨量雷达融合后的降雨数据Rf，即

Rf=F(R，G).

(7)

2 雨量雷达融合置信处理算法

在工程应用中，定量降雨估计常以雨量计降雨数据为准，利用二维插值技术[7-9]估计区域雨量。以雨量计站点数据插值的方法难以反映整体区域内的完整变异性，且在雨量计未覆盖区域估计精度下降明显。雨量雷达具有探测范围广、时空分辨率高等特点，但是受复杂环境影响，导致其精度不足。因此，本文拟提出融合置信处理算法，提高雨量雷达降雨估计精度。本算法在M≪N时，亦可实现线性无偏和均方误差最小[11]，同时对于雨量计布设密度不均问题，本算法全面分析区域内数据的空间相关性，使得融合后的数据更可靠，雨量雷达测量更稳定。

本文的融合置信处理算法，以协克里金法为基础[11]，综合变量的空间连续和变量间的相关性，以精度更高的雨量计数据为主变量，以雷达反射率因子为辅变量，采用不同的空间变异函数，运用协克里金法实现二者的数据融合，以提高雨量雷达降雨估计的精度。

2.1 标准化处理

由于雨量雷达反射率因子数量级相较降雨量数据差距过大，直接融合难以体现数据优势，本文先利用Z-score标准化方法[13]，实现变异性转换及标准化。Z-score标准化的公式如下：

(8)

(9)

(10)

经标准化后得雷达反射率因子RS为

(11)

其中Z(·)为标准化算子。

2.2 基于协克里金(CoKriging)算法的融合估计

协克里金估计算法是一种多元空间估计方法，利用存在区域协同关系(Coregionalization)的主、辅变量间的空间相关性，建立交叉协方差函数(Cross Covariance)和交叉变异函数(Cross Variogram)，融合分析多变量的空间相关性和统计相关性，实现区域变量的均方误差最小和线性无偏估计[11]，而雨量雷达和雨量计在降雨方面的测量，是非完全采样问题，属于协克里金估计中的特例。

因此，本文采用协克里金估计算法[11]融合雷达雨量反射率因子及雨量计数据，以较高精度的雨量计数据G和标准化后的雷达反射率因子RS分别为主、辅变量，由协克里金算法得到校正后雨量雷达数据，即

(12)

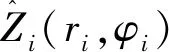
为求解式(12)中的权系数，下面简要介绍空间变异函数等基本概念。由空间变异理论[10]可知，主、辅变量的变异函数γR、γG及交叉变异函数γRG分别为

(13)

(14)

(15)

式中N′(γ)表示半径Δr内数据对的个数。

由估计子的均方误差定义可知[14]，协克里金算法融合后的均方误差为

(16)

将式(16)展开成协方差形式，即

(17)

式中CR(·)和CG(·)分别表示雨量雷达和雨量计数据的协方差函数；CRG(·)表示交叉协方差函数[11]。

由于协克里金估计算法是无偏且均方误差最小，因此，求解式(12)中主、辅变量的权系数等效为求解式(18)的约束优化问题，即

(18)

其中λ=[λ1，λ2，…，λN]T，ξ=[ξ1，ξ2，…，ξM]T。由优化理论可知，式(18)可转化成为无约束优化问题。由Lagrange乘子法可得：

(19)

式中μ1和μ2为Lagrange系数。

由无约束优化问题的求解方法[14]可知求解目标函数L的零梯度即可，即

∇L=0，

(20)

因此，由式(19)和式(20)得到N+M+2阶协克里金估计线性方程组，即

(21)

(22)

由线性代数理论[14]可将协克里金估计方程组表示成矩阵形式，即

AX=b，

(23)

其中A为变异矩阵，X为广义权系数矢量，b为广义交叉变异矢量，且

(24)

X=[λ1，…，λN，ξ1，…，ξN，μ1，μ2]T，

(25)

b=[γGR01，…，γGR0N，γG01，…，γG0M，1，0]T.

(26)

由最小二乘法(LS)[14]可得广义权系数矢量X为

X=(ATA)-1ATb，

(27)

将权系数矢量λ和ξ代入式(12)可得融合后雨量数据，即

(28)

(29)

2.3 相对置信度(Relative Confidence Degree，RCD)

针对雷达反射率数据动态变化范围大的问题，传统的绝对误差和相对误差难以反映雨量雷达的测雨性能，在雨量雷达全局误差分析方面，归一化的评价方法无法实现有效分析，因此，结合概率中的置信区间概念，本文提出了一种新的误差评判标准，即相对置信度，以实现误差的全局分析。

本文将相对置信度Cα定义为在给定相对误差门限α下，所有雨量雷达测量相对误差小于α的分辨单元数Nα与雷达测量分辨单元总数N之比，即

(30)

其中α定义为相对误差，即

(31)

由相对置信度的定义可知，相对置信度可分析不同相对误差门限下的雨量雷达校准误差的空间分布情况，从而反映校准后雨量雷达降雨数据的可信度。

综上所述，本文提出的雨量雷达融合置信处理算法流程图如图2所示。

图2 雨量雷达融合置信处理算法流程图

3 实测与仿真实验

设雨量雷达分辨单元数为N=71×71，随机选取雨量站位置，雨量雷达数据的随机误差满足高斯分布，仿真实验中每个数据点为100次Monte Carlo实验。

试验1分析雨量雷达和雨量计实测数据。图3(a)为2016年3月12日8时到16时PR-11A雨量雷达在江西省赣州市信丰县古陂河流域的雷达监测雨量分布图，图3(b)表示雨量雷达相对雨量计的相对误差，其最大相对误差高达70%，平均误差约为55%。因此，雨量雷达的准确度仍较低，须提高雨量雷达数据有效性。

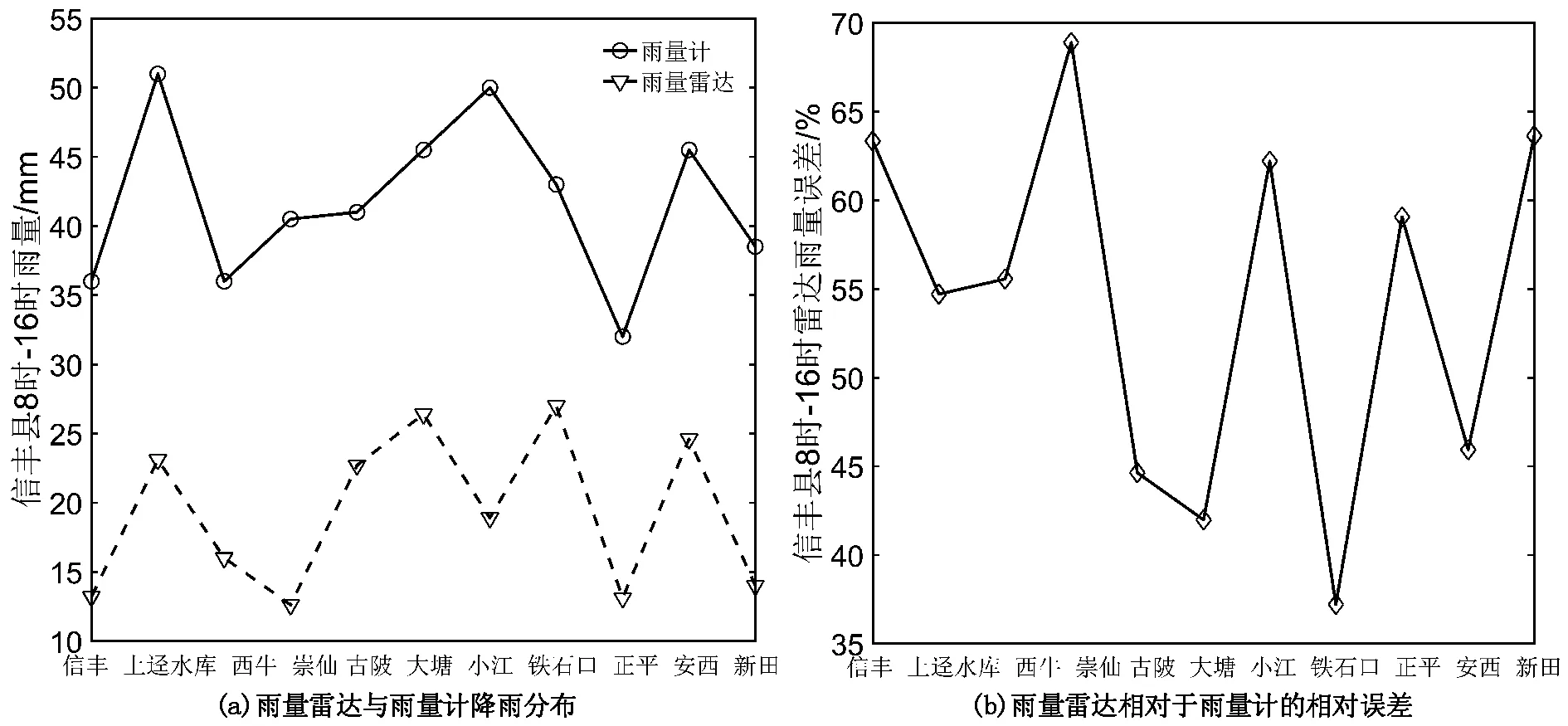
图3 PR-11A雨量雷达实测数据分析

图4 融合置信处理算法分析示意图

表1 不同降雨量参数设置

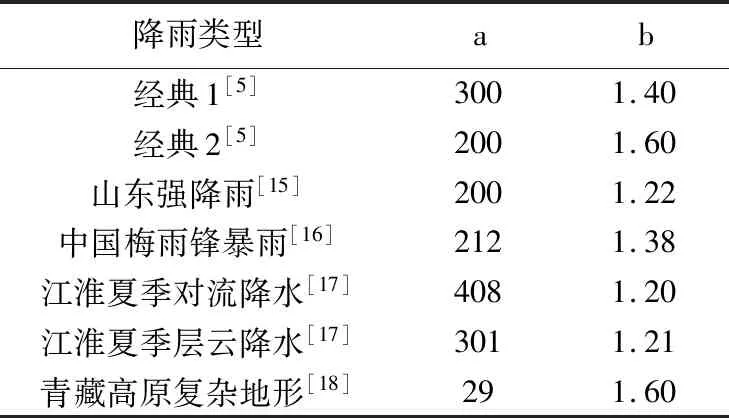
表2 不同降雨类型Z-R关系系数设置

试验4分析雨量计站点数M对融合置信处理算法的影响。仿真条件同试验3，利用相对置信度分析不同M时融合处理算法的性能。由图6可知，融合置信处理算法的相对置信度均优于其他算法，且对M不敏感，验证了融合置信处理算法对雨量计站点数M的稳健性。

图5 不同变异性下相对置信度分析

图6 不同M时相对置信度分析

4 结束语

针对雨量雷达测雨精度不足、雨量计测量范围有限的问题，本文结合空间变异理论和数据融合技术，提出了一种中小流域雨量雷达融合置信处理算法。该算法先对雨量雷达反射率因子数据进行标准化处理，实现变异性转换及标准化，再以标准化后雷达反射率因子作为辅变量，雨量计数据为主变量，利用协克里金法实现数据层融合，进行定量降水估计。实测数据与仿真结果表明，融合置信处理算法实现了雨量雷达与雨量计数据层融合，提高了雨量雷达的定量降雨测量的相对置信度，验证了本文融合置信处理算法的适用性与稳健性。本文为工程上雨量雷达的定量降水估计提供了理论指导，具有重要的工程意义。未来也将研究天空地多源降雨数据的融合技术，并结合深度学习等方法实现降雨估计及降雨趋势预测等。