新教材“拓广探索”栏目函数题赏析
2022-12-19王芳
王 芳
(江苏省苏州市常熟市梅李高级中学 215500)
人教版《数学新教材》拓广探索栏目在习题方面的设置比较好,注重培养学生的探究、创新精神,关注相关知识的综合运用,能够较好地提高学生的综合素养.为此,现选取必修第一册第三章《函数的概念与性质》、第四章《指数函数与对数函数》中有关特色习题加以具体阐释,旨在帮助同学们深刻领悟教材习题设置的良苦用心,进一步提高解题能力.
1 考查多个对数比较大小
例1 (教材第141页拓广探索栏目第13题)比较下列各题中三个值的大小:
(1)log0.26,log0.36,log0.46;
(2)log23,log34,log45.
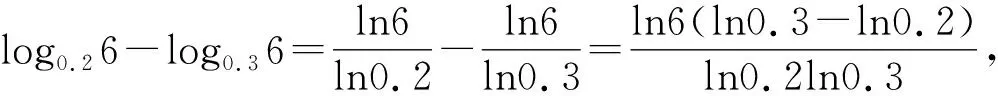
即log0.26>log0.36.
同样,作差可得log0.36>log0.46.
所以log0.26>log0.36>log0.46.
同样,作商可得log0.46 所以log0.26>log0.36>log0.46. 于是,根据0<0.2<0.3<0.4<1,得 f(0.2)>f(0.3)>f(0.4). 即log0.26>log0.36>log0.46. 同样,可知log45 从而有log23>log34>log45. 评注本题设计较好,关注比较大小的各种常用方法在解题中的运用.常用一般结论:(1)设函数f(x)=logxN,其中N>0,x>0且x≠1,则当N>1时,函数f(x)在区间(0,1)和(1,+∞)上均单调递减;当0 (1)探索函数f(x)的单调性; (2)是否存在实数a使函数f(x)为奇函数? 具体证明过程如下: 易知函数f(x)的定义域为R. 任取x1,x2∈R,且设x1 因为2x1<2x2,2x1+1>0,2x2+1>0, 所以f(x1) 故存在实数a=1,使函数f(x)为奇函数. 评注关于函数的单调性、奇偶性,若进行判断,则利用外在结构特点即可;若进行证明,则必须根据函数的单调性、奇偶性的定义加以证明.处理是否存在型问题,往往需要先假设存在,再进行合情推理、分析.若得到矛盾,则表明不存在;若没有得到矛盾,就会得到存在的具体情形. 例3(教材第102页拓广探索栏目第13题)如图1,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t),试求函数y=f(t)的解析式,并画出函数y=f(t)的图象. 图1 图2 综上,函数y=f(t)的图象如图2所示, 评注本题设计较好,侧重考查了数形结合思想、分类与整合思想在解题中的综合运用,同时也考查了分段函数的解析式与图象,显然能够较好地培养学生在直观想象以及数学运算方面的核心素养. (1)连续进行5次,容器中的纯酒精还剩下多少? (2)连续进行n次,容器中的纯酒精还剩下多少? 例5 (教材第87页拓广探索栏目第13题)我们知道,函数y=f(x)的图象关于坐标原点成中心对称图形的充要条件是函数y=f(x)为奇函数.有同学发现可以将其推广为:函数y=f(x)的图象关于点P(a,b)成中心对称图形的充要条件是函数y=f(x+a)-b为奇函数. (1)求函数f(x)=x3-3x2图象的对称中心; (2)类比上述推广结论,写出“函数y=f(x)的图象关于y轴成轴对称图形的充要条件是函数y=f(x)为偶函数”的一个推广结论. 解析(1)设函数f(x)=x3-3x2图象的对称中心为点(a,b),则函数y=f(x+a)-b为奇函数,即y=(x+a)3-3(x+a)2-b为奇函数. 根据奇函数的定义可得(-x+a)3-3(-x+a)2-b=-[(x+a)3-3(x+a)2-b],整理得(6a-6)x2+2a3-6a2-2b=0对任意x∈R恒成立,从而可知6a-6=0,且2a3-6a2-2b=0,解得a=1,b=-2. 故所求函数图象的对称中心为点(1,-2). (2)类比思维,可知推广结论为:函数y=f(x)的图象关于直线x=m成轴对称图形的充要条件是函数y=f(x+m)为偶函数. 总之,结合上述举例解析可知,人教版《数学新教材》拓广探索栏目在习题方面的设置是比较成功的,不仅关注习题本身的探索性、创新性、综合性,而且关注培养学生分析问题、解决问题的实际能力,能够较好地提高学生对所学知识、方法的综合运用能力,进而提升学生在直观想象、逻辑推理、数学抽象、数学运算以及数学建模方面的核心素养.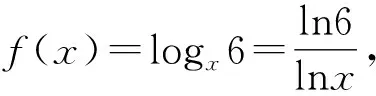
2 考查含参函数的性质
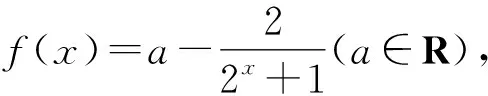
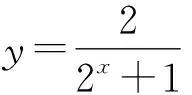
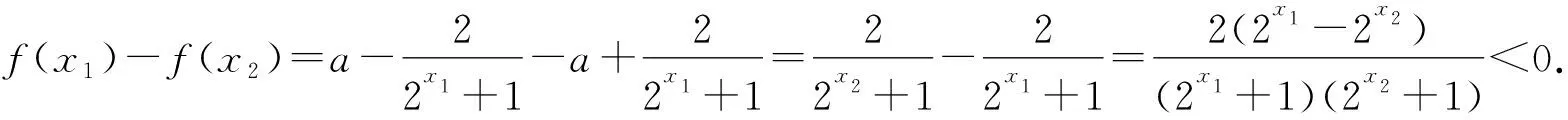
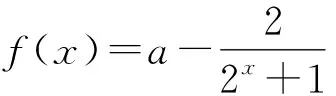
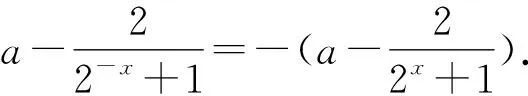
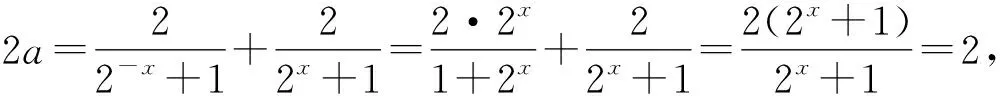
3 考查数学思想在函数问题中的应用
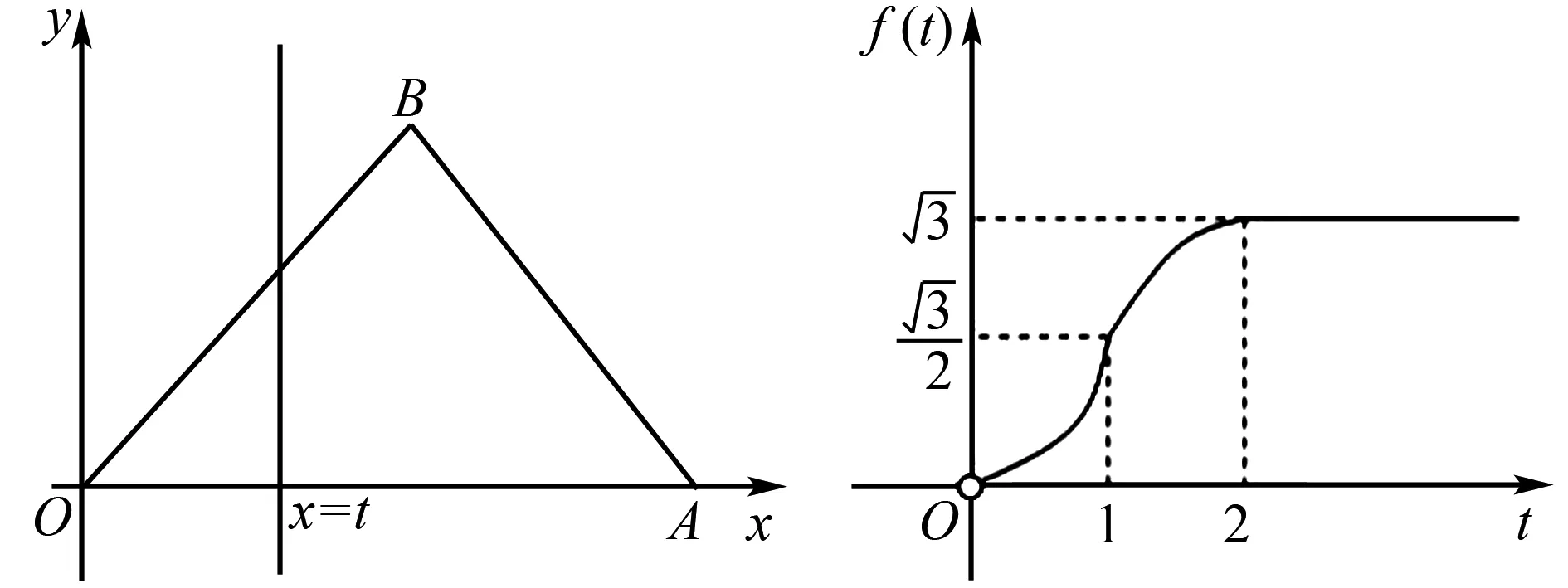
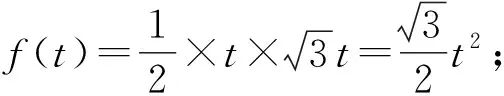
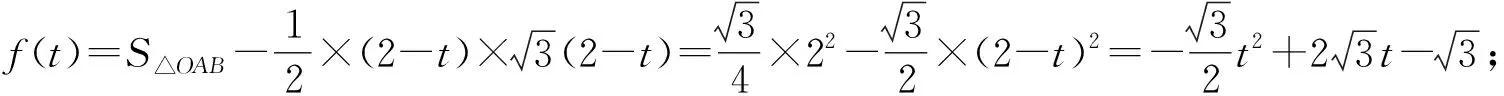
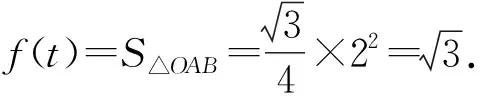
4 考查指数函数与归纳推理的交汇
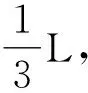
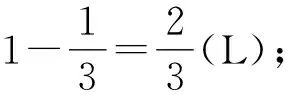
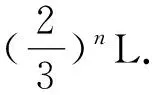
5 考查函数图象的对称性与类比推理的交汇