对数比较大小试题的解法探究两例
2022-12-19李鸿昌
李鸿昌
(贵州省北京师范大学贵阳附属中学 550081)
1 课本习题
例1(2019年人教A版《数学必修第一册》第141页13题)比较题中三个值的大小:
log23,log34,log45.
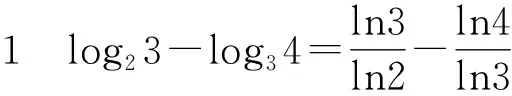
由基本不等式可知
所以log23>log34.
同理可得log34>log45.
综上所述,log23>log34>log45.
解法2 由糖水不等式可知
即log32 所以log23>log34. 同理可得log34>log45. 综上所述,log23>log34>log45. 点评基本不等式和糖水不等式是解决这一类对数比较大小试题的常用方法.高考题源于课本而高于课本,这需要我们对课本的例题和习题做深入的研究,通过研究,可以将例1作如下推广. 推广1 设n∈N*且n>1,则 logn+1n 证法1 因为 由基本不等式知, 所以logn+1n 证法2 由糖水不等式得 =logn+2(n+1). 由推广1可得到本习题的推广: 推广2设n∈N*且n>1,则 logn(n+1)>logn+1(n+2). 证明由logn+1n 即logn(n+1)>logn+1(n+2). 推广3设a>b>1,m>0,则 logab 证明由糖水不等式得 =loga+m(b+m). 上述的推广1和推广3,我们通常形象地称其为“对数型糖水不等式”.我们还可以将推广2作如下推广. 推广4若x>1,则函数f(x)=logx(x+1)在(1,+∞)上单调递减. 由1 所以xlnx<(x+1)ln(x+1). 因此,当x>1时f′(x)<0,所以函数f(x)=logx(x+1)在(1,+∞)上单调递减. 推广5 若x>1,b>0,则函数f(x)=logx(x+b)在(1,+∞)上单调递减. 证明由换底公式,有 由于x>1,b>0,则 1 从而xlnx<(x+b)ln(x+b). 所以f′(x)<0. 因此函数f(x)=logx(x+b)在(1,+∞)上单调递减. 由此可得:当a>1,b>0,c>0时,有 通过连续运行系统3h,每间隔0.5h测1次数据,设定系统每分钟雾化0.2mL水为工作方式一;每分钟雾化0.4mL水为工作方式二。经实验测得数据如表1和表2所示。两种方式下实际产生的雾化量和设定值基本一致,系统能够实现无线远距离控制。通过间断和连续运行测试,实验结果表明系统各部分工作正常,能满足超声波雾化系统智能检测、自动控制、远程集群监控和高稳定性低功耗的要求。 loga(a+b)>loga+c(a+b+c). 例2(2020年全国Ⅲ卷理科12题)已知55<84,134<85.设a=log53,b=log85,c=log138,则( ). A.a C.b 解法1 由55<84,得 log855 所以5b<4. 由134<85,得log13134 所以5c>4. 因为34<53, 所以4a=4log53=log534 因为54>83, 所以4b=4log85=log854>log883=3, 综上所述,a 故选A. 解法2a-b=log53-log85 所以a 因为b=log85, 得8b=5. 所以85b=55<84. 所以5b<4. 因为c=log138, 所以135c=85>134. 所以5c>4. 综上所述,a 故选A. 解法3 由基本不等式得 =log53×log58 所以a 综上所述,a 解法4 由题意及糖水不等式可知 用排除法可知选项A正确. 点评对于b和c,由参考数据55<84,134<85,可以直接用对数或者化为指数进行比较大小;而对于a和b,需要用到34<53,83<54,这是题目没有给出的,需要考生通过类比去发现,这就得到了解法1,考查了类比思想和数学运算能力. 解法2和解法3,主要是通过作差或者作商来比较a和b的大小.而作差或者作商之后,都需要用到基本不等式,这是值得重视的. 用与解法1类似的方法,可以比较出log32与log53的大小: 因为23<32, 所以3log32=log323 又因为52<33, 结合解法1的结果,可以得到 设Fn是斐波那契数列(Fibonacci):1,1,2,3,5,8,13,21,34,55,…,即F1=F2=1,当n≥3时,Fn=Fn-1+Fn-2.我们观察到上述不等式链中对数的底数和真数组成的数列2,3,5,8,13恰好是斐波那契数列的一个子列,通过探究可得: 由此可见,本题是以斐波那契数列为背景,考查数列{logFn+1Fn}的单调性或者其数值的取值范围,这样该题不仅融合了指数与对数的运算,也融入了数学史知识,渗透了数学文化. 因为数列{logFn+1Fn}单调递增,所以数列{logFnFn+1}单调递减,且前面几项的数字不大,可以不提供参考数据,于是得到变式1. 变式1 设a=log23,b=log35,c=log58,则( ). A.a C.a 解析由糖水不等式得 同理可得log35 即a 根据例1及其推广,可得到如下的变式题. 变式2 设a=log34,b=log56,c=log78,则( ). A.a C.a 解析由推广2知,log23>log34>log45>log56>log67>log78,所以c 变式3 设a=log35,b=log57,c=log79,则( ). A.a C.a 解析由推广5知,当x>1时,函数f(x)=logx(x+2)在(1,+∞)上单调递减. 所以f(3)>f(5)>f(7). 即c 变式4 设a=log63,b=log74,c=log85,则( ). A.a C.a 解析由推广5知,当x>1时,函数f(x)=logx(x+3)在(1,+∞)上单调递减. 所以f(3)>f(4)>f(5). 即log36>log47>log58. 所以log63 即a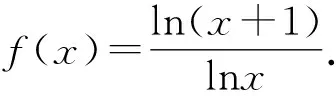
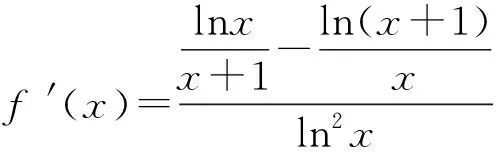
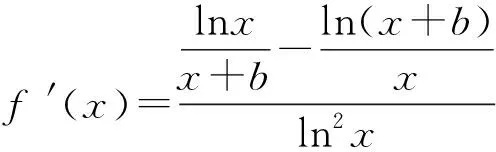
2 高考试题
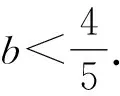
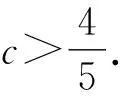
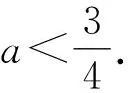
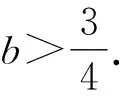
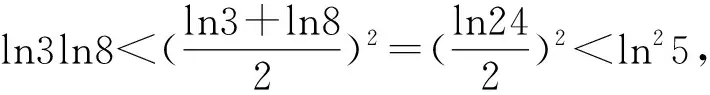
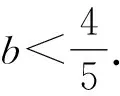
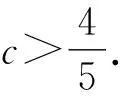
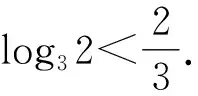
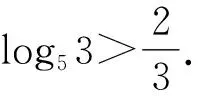
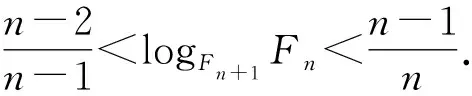
3 变式应用
