多视角探究一道2022年模考题

贺凤梅

(新疆维吾尔自治区伊犁州巩留县高级中学 835400)

高考和模考都经常针对圆锥曲线的对称性命题，既有大题也有小题，理论是相近的，但运算却有明显差异.我们可以利用角平分线性质、二倍角、到角等知识来解答，只有比较才能发现自己喜欢的简捷解法.下面以一道2022年模考题为例，展示解法，并推广出一般情形.

1 呈现试题

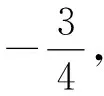
(1)求C的方程；

(2)已知点F(1,0)，直线l:x=4与x轴交于点D，直线AM与l交于点N.是否存在常数λ，使得∠MFD=λ∠NFD？若存在，求λ的值；若不存在，说明理由.

2 探究解法

解析几何中有关角度问题有很多解决策略，可以转化为斜率来求解；如果涉及到求参数的值，突破策略是由特殊情况求解，求出参数的值，一般情况验证成立即可；如果是2倍角关系，可以采用角平分线的性质、到角公式或正切的二倍角公式来求解；在具体的求解过程中，可以直接设直线的斜率，也可以借助于设其中一个点的坐标，联合直线和曲线方程来求解；还可以借助于圆锥曲线上的点，采用设而不求的方法解决.此类题入口宽，多视角、多方法均可完成解答.

3 解答试题

第(2)问，由(1)可知，F1(1,0)为其右焦点.

根据对称性，不妨设点M在x轴上方，则点N也在x轴上方.

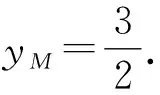
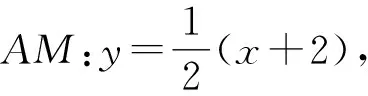
故∠MFD=2∠NFD，因此存在实数λ=2，使得∠MFD=λ∠NFD.

据此，可以猜测实数λ=2.以下进行具体论证.

视角1 直接设AM的斜率求解.

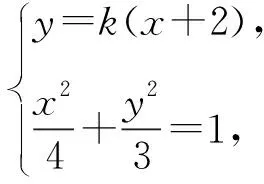
(4k2+3)x2+16k2x+16k2-12=0.

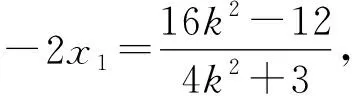
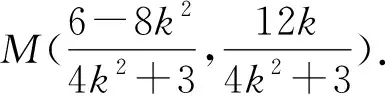
在y=k(x+2)中，令x=4,得

y=6k，即N(4,6k).

所以直线MF:4kx+(4k2-1)y-4k=0.

点N(4,6k)到MF的距离

而点N到DF(即x轴)的距离为6k，

所以NF是∠MFD的角平分线.

即∠MFD=2∠NFD.

因此存在实数λ=2，使得∠MFD=λ∠NFD.

评注此解法属于常规解法，根据特殊位置的求解，猜测是二倍关系，所以考虑点N在∠MFD的角平分线上，通过上面的计算得到了验证.

解法2(借助正切二倍角公式)

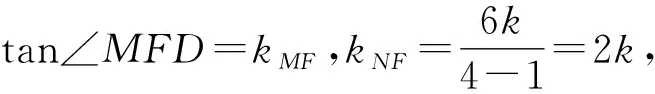
由正切二倍角公式,得

所以tan∠MFD=tan2∠NFD.

结合图形知，∠MFD，∠NFD均为锐角，

所以∠MFD=2∠NFD.

因此，存在实数λ=2，使得∠MFD=λ∠NFD.

评注由数形结合可知，两角的其中一边均为x轴的正半轴，所以满足tan∠MFD=kMF，tan∠NFD=kNF，因此要找两角的关系，可通过两角的正切关系来判断，进一步通过对应的斜率关系来判断，找到了解决的思路和关键点，问题也就迎刃而解了.

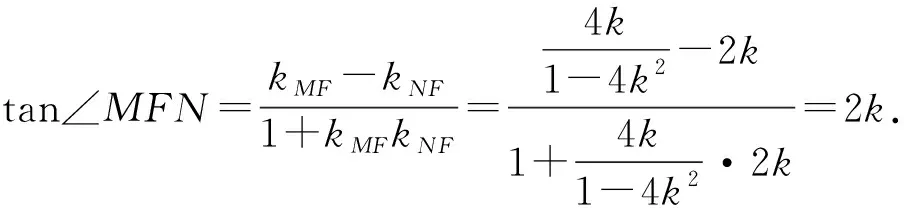
而tan∠NFD=2k，

所以tan∠MFN=tan∠NFD.

结合图形知，∠MFN，∠NFD均为锐角，

所以∠MFN=∠NFD.

因此NF是∠MFD的角平分线.

即∠MFD=2∠NFD.

故存在实数λ=2，使得∠MFD=λ∠NFD.

评注解法3中用到了到角公式，现行教材已经不涉及，不过老师们还是可以适当了解，针对程度好的学生，也可以适时介绍，拓宽学生的解题思路.

视角2借助于点N的坐标及正切的二倍角公式求解.

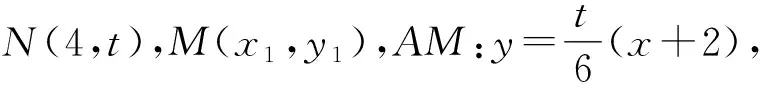
(t2+27)x2+4t2x+4t2-108=0.

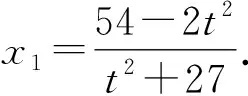
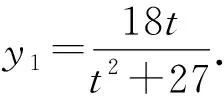
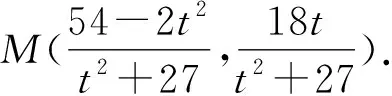
由斜率公式,得

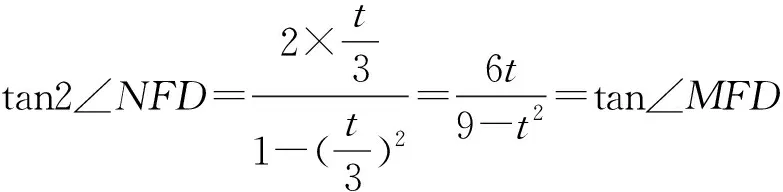
即∠MFD=2∠NFD.

因此存在实数λ=2，使得∠MFD=λ∠NFD.

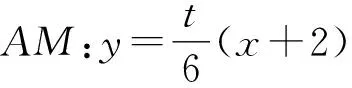
视角3 借助于点M的坐标求解.

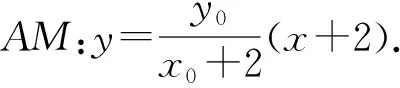
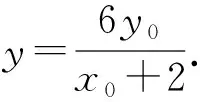
由正切的二倍角公式,得

①

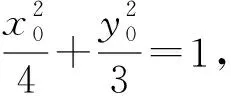
即∠MFD=2∠NFD.

因此存在实数λ=2，使得∠MFD=λ∠NFD.

评注此解法是设点M的坐标，表示直线AM的方程，将点N的坐标求出，同时借助于点M在曲线C上，满足曲线方程，不需要联立而将两角的正切值用点M的坐标巧妙表示，成功求解，值得借鉴和运用到解题中去.

文中多视角、多方法解答了此题，但如果止步于此，也只是解答了一道题.进一步思考，此题能不能推及一般呢？在椭圆中成立，双曲线中是否也有相同或相似的结论呢？以下通过推导来进行验证.

4 椭圆中的一般推广

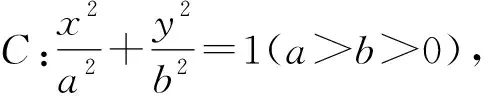
利用解法1推导与证明一般情形如下：

AM:y=k(x+a)，M(x1,y1)，

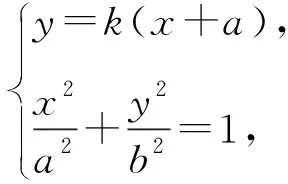
(a2k2+b2)x2+2a3k2x+a2(a2k2-b2)=0.

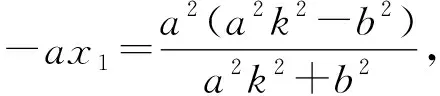
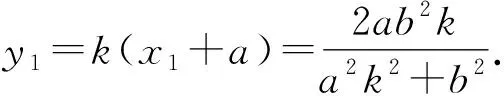
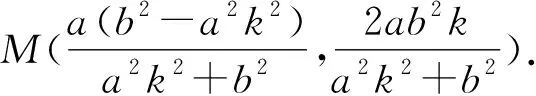
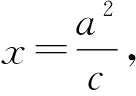
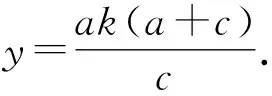
利用斜率公式求得

由正切的二倍角公式,得

即∠MFD=2∠NFD.

因此存在实数λ=2，使得∠MFD=λ∠NFD.

5 双曲线中的一般推广

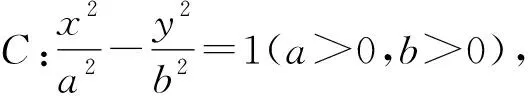
利用解法1推导与证明一般情形如下：

AM:y=k(x+a)，M(x1,y1)，

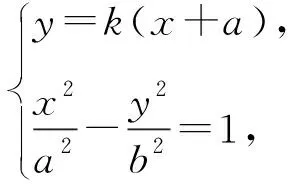
(b2-a2k2)x2-2a3k2x-a2(a2k2+b2)=0.

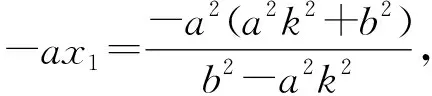
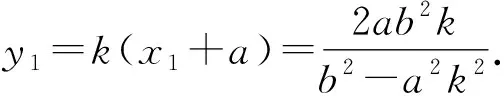
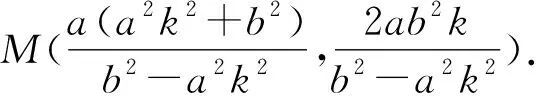
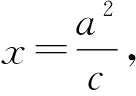
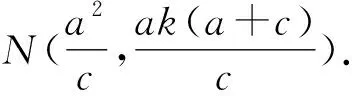
利用斜率公式求得

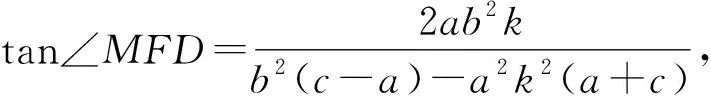
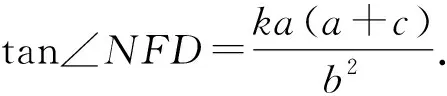
由正切的二倍角公式,得

即∠MFD=2∠NFD.

因此存在实数λ=2，使得∠MFD=λ∠NFD.

在高中数学新课改全面推行的形势下，高中数学学科教学内容、模式和方法也是当代教育研究的热点.为了实现数学教学的时效性，教师必须做到全方位思索，多角度为学生提供解题思路.而一题多解是目前高中数学教学所研究的方向之一，且一题多解思维属于创建“变式教学”体系，在该过程中，学生的数学思维也被发散、开放，思维得到了有效地锻炼和提高.

另外，对于一些具体问题，我们可以通过推广拓展至一般情形，从而深入地分析和解决问题，能很好地将知识系统化.