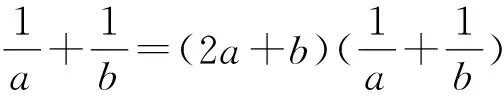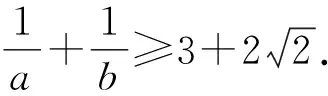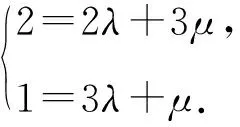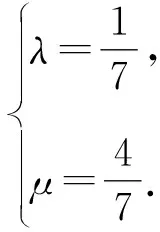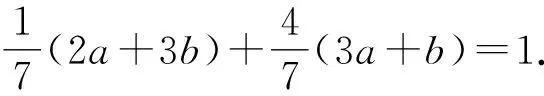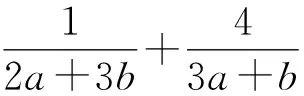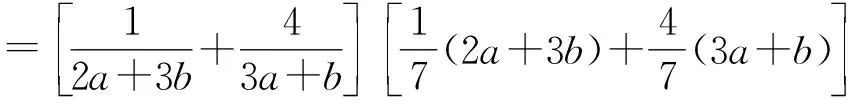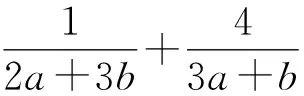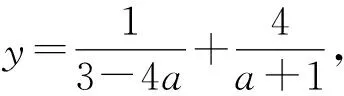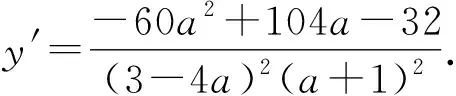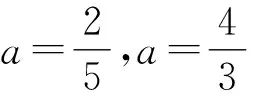解题反思下的高三数学复习
2022-12-19胡贵平
胡贵平
(甘肃省白银市第一中学 730900)
高三数学复习离不开解题,如何高效地解题决定了高三数学复习的成败,充分发挥解题后的总结与反思,深入挖掘题目所蕴含的知识本质、引导学生在复习中收获更多的感悟,领会其中的数学思想方法,这样才会获得高效、扎实的复习效果.
1 反思解法
一个数学问题可能有多个方法解决,多个视角思考可以培养思维的发散性,得出最简捷的解法.有些是通解通法,有些是巧解妙法,一定要反思对一类题型极具指导和启发意义的通解通法,不仅要研究其解法更要探寻本质.
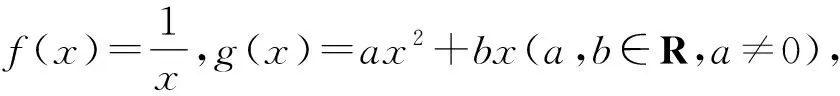
A.当a<0时,x1+x2<0,y1+y2>0
B.当a<0时,x1+x2>0,y1+y2<0
C.当a>0时,x1+x2<0,y1+y2<0
D.当a>0时,x1+x2>0,y1+y2>0
解法1在同一坐标系中分别画出两个函数的图象,要想满足条件,如图1,作出点A关于原点的对称点C,则点C坐标为(-x1,-y1).
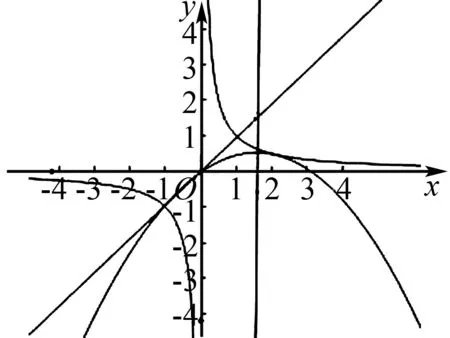
图1
由图象知-x1
即x1+x2>0,y1+y2<0.故选B.
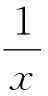
则1=ax3+bx2(x≠0).
设F(x)=ax3+bx2,
则F′(x)=3ax2+2bx.
令F′(x)=3ax2+2bx=0,
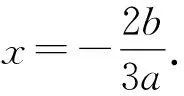
要使y=f(x)的图象与y=g(x)图象有且仅有两个不同的公共点,只需
整理,得4b3=27a2.
于是可取a=±2,b=3来研究:
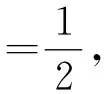
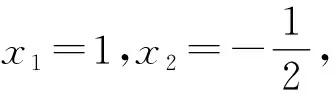
故选B.
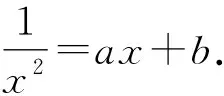
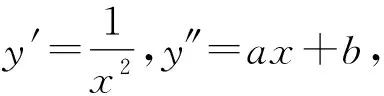
即-x1>x2>0.
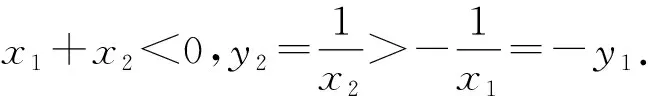
即y1+y2>0.
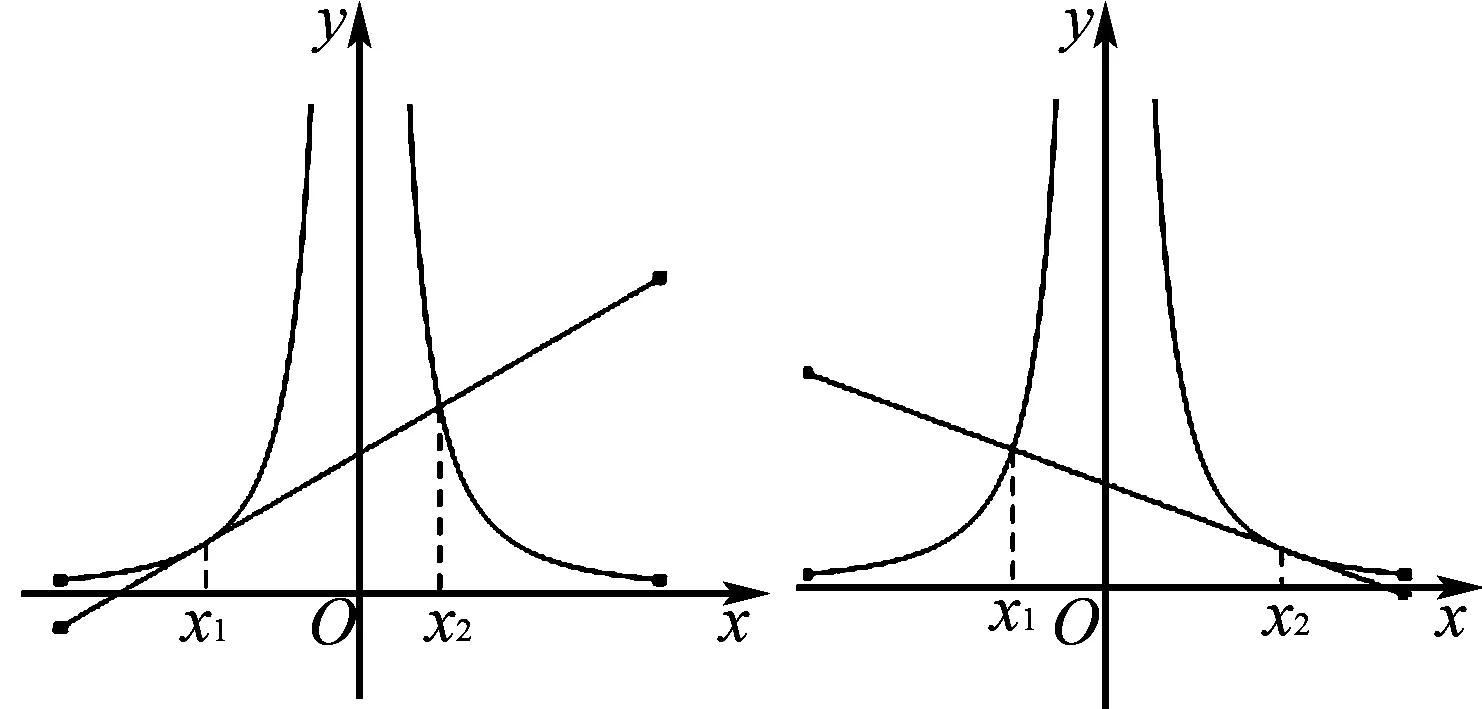
图2 图3
同理由图3经过推理可得当a<0时x1+x2>0,y1+y2<0.
故选B.
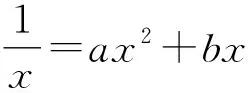
即三次方程ax3+bx2-1=0有两个不同的实数根,且其中一个是重根,不妨记为x1,则
因为a≠0,所以x1x2≠0,x1+2x2=0.
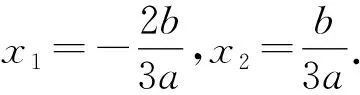

即4b3=27a2.
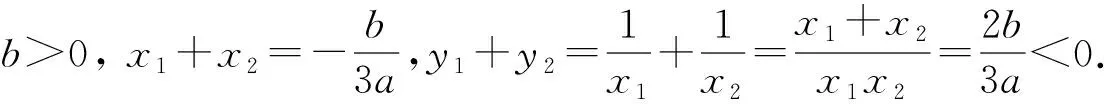
所以当a<0时,x1+x2>0,y1+y2<0.
以上四种方法从不同的角度都解出了这道题,反思这些解法,还能解决怎样的问题,解法的实质是什么,能否推广?

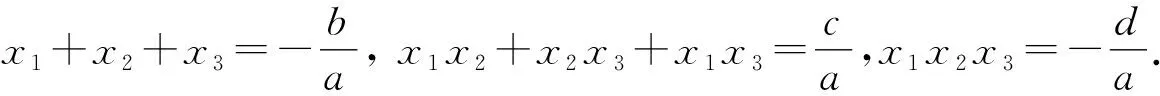
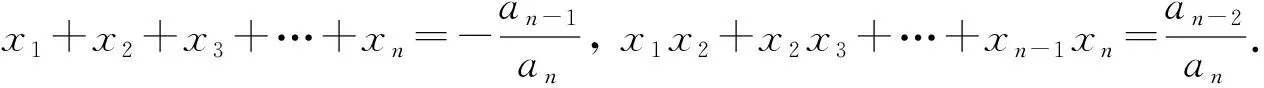
2 反思原理
反思解题过程中用到的基础知识,注重知识的形成过程,寻找问题与知识结构之间的联系,探究巧妙转化和灵活应用,通过解题反思揭示数学问题的本质,升华解法的理解.
例2 已知在ΔABC中,A=60°,AC=6,BC=k,若△ABC有两解,则正数k的取值范围为____.

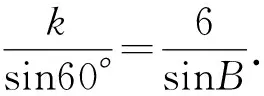
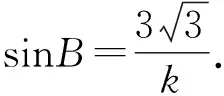
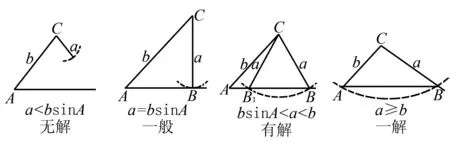
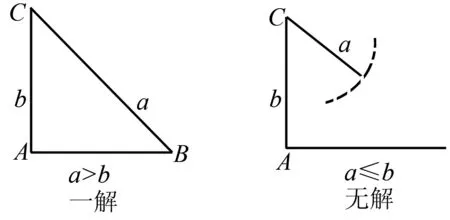
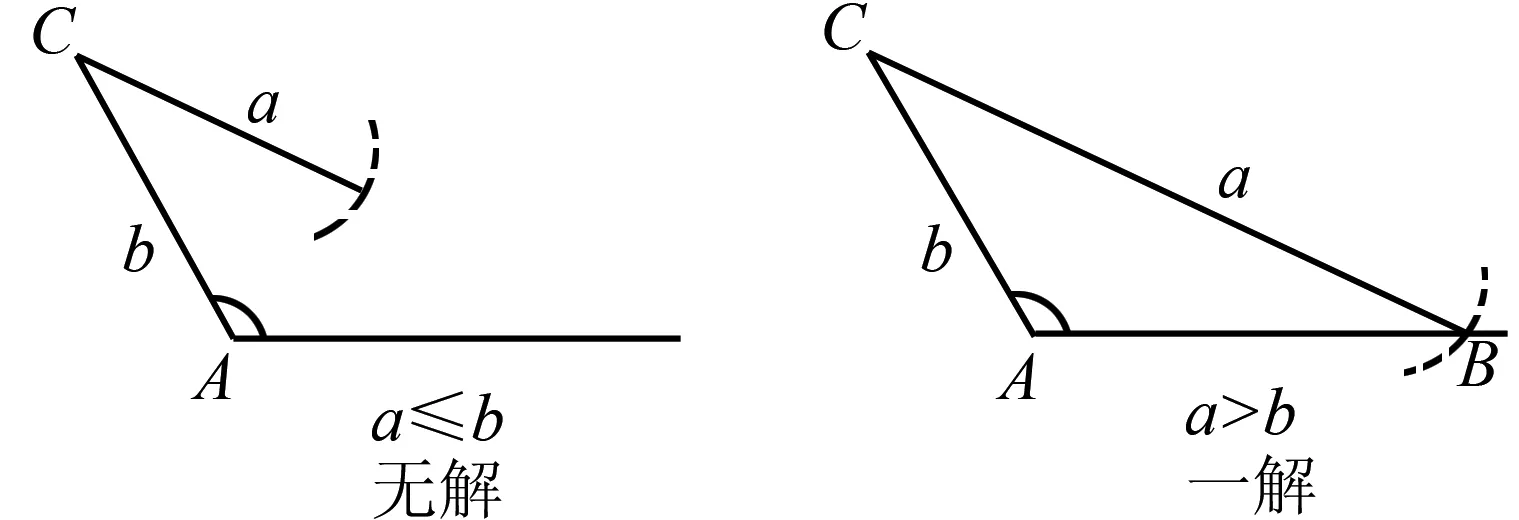
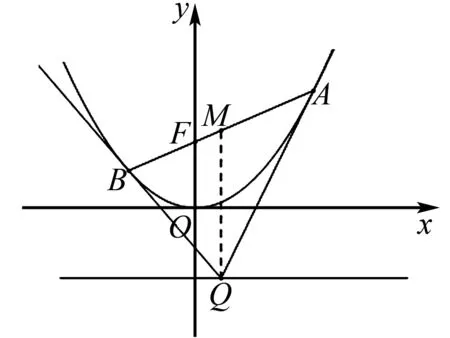
因为0° 在△ABC中,设BC=a,AC=b,边a的对角为A,则三角形解的情形如下: (1)A为锐角时,如图4: 图4 (2)A为直角时,如图5; 图5 (3)A为钝角时,如图6: 图6 高考中经常出现浓厚数学背景的题,把中学数学知识迁移到不同情境中去,反思题目的背景,探究“源”,寻觅“流”, 多方位、全角度地延伸演变,充实知识结构,开拓数学视野. 例3 (2018年新课标Ⅲ卷)已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°,则k=____. 解析依题意得,抛物线C的焦点为F(1,0),故可设直线AB:y=k(x-1). k2x2-(2k2+4)x+k2=0. 设A(x1,y1),B(x2,y2),则 y1y2=k2[x1x2-(x1+x2)+1]=-4. =x1x2+(x1+x2)+1+y1y2-(y1+y2)+1 所以k=2. 这道题的背景是阿基米德三角形,复习中可以以高考题为载体,展开阿基米德三角形简单性质的探究. 抛物线的弦与过弦的端点的两条切线所围的三角形,称为阿基米德三角形.阿基米德三角形有如下常见结论: 如图7,已知Q是抛物线x2=2py准线上任意一点,过点Q作抛物线的切线QA,QB分别交抛物线于A,B两点,Mx0,y0为AB中点. 图7 (1)若AB过焦点,则AB端点的两条切线的交点Q在其准线上; (2)阿基米德三角形底边上的中线平行于坐标轴,即xQ=xM; (3)AB过抛物线的焦点; (4) 若AB过焦点,则AQ⊥BQ; (5)若AB过焦点F,则FQ⊥AB; (6)若AB过焦点,则阿基米德三角形面积的最小值为p2. 根据结论5,很容易解决这个问题,设抛物线C的焦点为F,则FM⊥AB. 所以k·kFM=-1. 所以k=2. 解完一道题后,反思解题方法中有无规律可循,提炼并总结出这一类题的解法.表象不同,但实质却相同,基于转化策略,强化迁移能力,类比出一般情形下的解题方法. 解法1 (“1”的代换法) 由于a,b∈R+,2a+b=1, 解法2 (导数法)由于a,b∈R+,2a+b=1,则 本题解法很多,可以用“1”的代换法、基本不等式法、代入消元法、柯西不等式法、三角换元法、判别式法、导数法等.要提高难度,只需进行变式.比如将条件等价变形,清除原来的痕迹,或将条件变换,使其看不清实质条件,还可以改变设问方式增加难度. 解法1(“1”的代换法) 圆x2+y2-4x-2y+1=0 的圆心为(2,1),所以2a+b=1. 设2a+b=λ(2a+3b)+μ(3a+b), 解法2 (导数法) 圆x2+y2-4x-2y+1=0 的圆心为(2,1),所以2a+b=1. 由于a>0,b>0,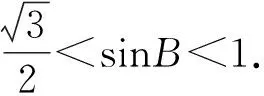
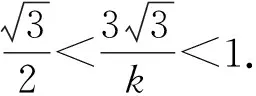




3 反思背景
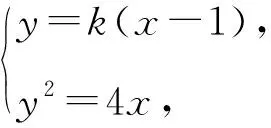
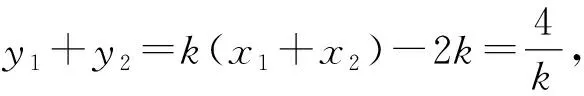
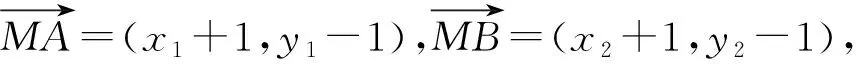
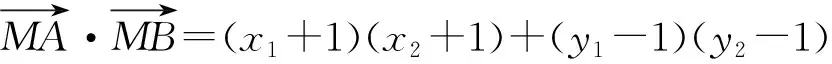

4 反思变式