深层次剖析一组从电场到磁场轨迹拼接问题
2022-12-19李鑫
李 鑫
(浙江省桐乡第一中学 314500)
1 引言
首先我们遴选两道高考真题,且看带电粒子从电场飞行到磁场过程中的轨迹,蕴藏了怎样的相似性.
(2018新课标卷二理综第25题)一足够长的条状区域内存在匀强电场和匀强磁场,其在xoy平面内的截面如图1所示:中间是磁场区域,其边界与y轴垂直,宽度为l,磁感应强度的大小为B,方向垂直于xoy平面;磁场的上、下两侧为电场区域,宽度均为l′,电场强度的大小均为E,方向均沿x轴正方向;M、N为条状区域边界上的两点,它们的连线与y轴平行.一带正电的粒子以某一速度从M点沿y轴正方向射入电场,经过一段时间后恰好以从M点入射的速度从N点沿y轴正方向射出.不计重力.
(1)定性画出该粒子在电磁场中运动的轨迹;
(2)求该粒子从M点射入时速度的大小;


图1
(1)区域Ⅰ加电场、区域Ⅱ不加磁场时,求在屏上探测到质子束的外加电场的最大值Emax;
(3)当区域Ⅰ加电场E小于(1)中的Emax,质子束进入区域Ⅱ和离开区域Ⅱ的位置等高,求区域Ⅱ中的磁场B与区域Ⅰ中的电场E之间的关系式.

图2
2 对比分析
全国卷试题的核心设问是第二问,第三问是给定问题下的具体求解,考查的是基本功.浙江题的前两问是基础设问,第三问才是精髓.我们直接比较两道题关键设问的粒子运动轨迹,如图3:

图3
图3(b)是全国卷的压轴题粒子轨迹,作为对比,笔者把浙江题粒子轨迹逆时针旋转90°,得到图 3(a),显然这不影响问题本质,可以清晰看出,两道题同出一源.
全国卷试题在浙江题基础上做了细节的修改,如表1:

表1
上述四点不同全都是细节上的不同.两题核心是一致的,就是考查粒子从电场进入磁场轨迹拼接处转折点,解题的关键是把握住从电场到磁场的偏转角.以浙江题为例:
设质子进入磁场时的速率为v′,如图3(a),
(1)
由几何关系知
中密度纤维板比较热市的产品主要集中在9、12、18 mm规格产品上。中密度纤维板也面临着和胶合板几乎同样的发展困难,那就是原材料的价格疯涨,致使中密度纤维板的出厂价格水涨船高,但是市场价格却不敢调高。据说中密度纤维板销售形势虽然好转,但面临下游生产厂家拖欠资金的问题挺严重。所以总的来看,中密度纤维板市场虽然复苏的迹象明显,但市场资金回笼状态还是不容乐观。
(2)
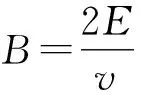
(3)
全国卷这道题只需要对(3)式做一些简单修改就可以了.
3 追本溯源
下文先分析这个问题的难点,再寻觅这一类问题的演化过程.学生在解题时,很难一开始就触摸到参考答案所用方法.参考答案敏锐地把握住了轨迹衔接速度偏转角这种方法,而且很明智地使用了偏转角的正弦关系.而一般学生很容易使用正切去解决问题.用偏转角正弦做联系可以巧妙地消参,但在考场上是不容易短时间摸索出来的.
4 试题背景
此题精华集中在利用速度偏转角的正弦进行消参,由于物理参量较多,学生们容易在解题过程中迷失.但是精巧的解题策略是无迹可寻的吗?其实不然,这样的问题并不是横空出世的,关于这一类的问题早已有之,在各地市的模考卷中都有体现,比如下面这个问题,可以说是这类问题的题源.
如图4,射入磁场和射出磁场的M、N两点间的距离d随着U和v0的变化情况为……

图4
此题做定性分析,很容易认为偏转电压越大,粒子的速度越大,所以在磁场中飞行时偏转半径越大,从而认为M,N两点的距离增大.
实际上,仍然抓住从磁场到电场偏转的角度,可以有

从这个例子可以看出,此题处理方式正是上面两道题解题的关键之处,所谓大道至简,莫过如此.这样的问题,想必学生在上高考考场前都练习过,但是再遇到高考题时,却很难把这样的解题历程迁移过来,甚至经过启发思考,学生都想不起来曾练习过类似问题.
接下来我们进入“刻意练习”时段,一起来训练这一定式结构下演化出的精彩的物理问题:
如图5(a),在直角坐标系X≤0的区域存在磁感强度大小为2B0的匀强磁场,在X>0的区域存在如图5(b)变化的匀强磁场,两磁场方向均垂直纸面向内,在t=0时刻有一质量为m,带电量为+q的带电粒子以大小为v0的初速度沿+X方向从O点进入磁场(不计粒子重力).
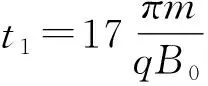


图5
评析这道题前两问是常规问题,妙笔在于第三问,实际上就是上述问题中的一个基本结论,即带电粒子在匀强磁场中仅受到洛伦兹力,其竖直方向上的位移仅和水平速度有关.那么这个结论还有更深层次的原因么?前文的阐述是一个关于角度处理的技巧,但是接下来我们要展现更深层的原因:
带电粒子在匀强磁场中仅受洛伦兹力,即:fxΔt=Δmvx=qvyBΔt=qBy


