例谈构造方程在解题中的应用

吴俊明

(广东省华南师范大学数学科学学院 510407)

学生在高中数学的解题中，相比于自己构造方程，更多地会遇到直接解方程的情形.而有时候，利用构造方程的方法，可以将一个复杂的问题变得简单.所谓构造方程的方法，是指根据题目已有信息构造方程，再利用所构造方程的解或者性质返回得到原问题的解.

1 在证明等式与不等式中的应用

证明由已知式子通分易得

(a+b)bsin4x+(a+b)acos4x=ab.

从而得到关于a的一元二次方程

a2cos4x+ab(cos4x+sin4x-1)+b2sin4x=0.

计算得关于此方程的根的判别式为

Δ=b2(cos4x+sin4x-1)2-4b2cos4xsin4x

=b2(cos4x+sin4x-1)2-(2cos2xsin2x)2

=b2(cos2x+sin2x)2-1(cos2x-sin2x)2-1

=0.

由于b>0，故

又因为sin2x+cos2x=1，

证明当-7a+b-3c=0时，命题显然成立.当-7a+b-3c≠0时，构造关于x的一元二次方程

(-7a+b-3c)x2+2(a-3b+4c)x+5(a+b-c)=0.

注意到该一元二次方程有一实根1，那么关于此方程的根的判别式为Δ=4(a-3b+4c)2-20(-7a+b-3c)(a+b-c)≥0.

化简即得(a-3b+4c)2-5(-7a+b-3c)(a+b-c)≥0.

评注本题中，根据求证式子的形式，容易让人联想到一元二次方程根的判别式，在给原求证式乘上系数4后，只需用该式中的若干多项式作为系数构造恒有解的一元二次方程即可.

2 在求值中的应用

例3 求sin18°和cos36°的值.

新一轮基础教育课程改革明确提出要求教师积极突破传统的教学模式，转变以往以教师说教为重点的教学方式，要求教师明确自身在教学中引导者与组织者的身份，并充分发挥自身的引导者与组织者的重要作用。在初中道德与法治课堂教学中，教师应该积极的优化教学的方法，以适合初中生身心特点和符合初中生兴趣的方式开展道德与法治教学，有效激活初中生的思维，从而达到事半功倍的效果。

-sin18°+cos36°=sin54°-sin18°

由于-sin18°<0，cos36°>0，

评注本题的主要思路是将-sin18°和cos36°看作某个一元二次方程的两根，利用韦达定理将该一元二次方程构造出来，从而解该方程即可求得-sin18°和cos36°的值.

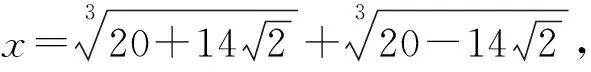
那么x3=40+6x.

于是考虑方程x3-6x-40=0，

即(x-4)(x2+4x+10)=0.

因为x2+4x+10=(x+2)2+6>0恒成立，

所以x-4=0.

即上述方程有唯一实根x=4.

3 在解方程(组)中的应用

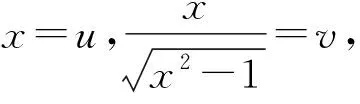
将原方程两边平方可得

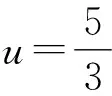
评注本题首先引入双变元u,v，看似将问题变复杂了，但实际上由原方程可得u+v的值，从而可将u,v看作是某个一元二次方程的两根，为此只需求出uv的值.此后，解由u,v得到的一元二次方程，即可得到x=u的值.

评注观察两根式内式子的系数，发现两根式内式子相减为一常数，于是两相加根式乘与之“对偶”的相减式，即可得到一个恒成立的方程.利用原方程，容易算得相减式的值，从而得到两个根式的值.再利用其中一个根式的值解方程即得原方程的解.

例7 解关于u,v,w的方程组

(1)

(2)

(3)

其中a,b,c是互不相等的实数.

解析将上述方程组中的三个式子相加得

3u+2(a+b+c)v+2(a2+b2+c2)w

=2(a3+b3+c3).

(4)

由(4)-2×(3),(4)-2×(2),(4)-2×(1)可以分别得到(5)(6)(7)，即

(5)

(6)

(7)

那么a,b,c是该一元三次方程的三个不同根.

从而由韦达定理得

即u=2abc,v=-ab-bc-ac,w=a+b+c.

经检验，这确实是原方程组的解.

评注本题首先要将由(1)(2)(3)式得到的方程组化简为由(5)(6)(7)式得到的方程组，再由(5)(6)(7)式的规律性容易想到构造与之相关的一元三次方程，从而利用韦达定理即可得到原方程组的解.在整个过程中，变元与系数相互转化的思路起到了重要作用.

构造方程的方法可以概括为以下几点：

(1)根据已知条件直接变形导出所需的方程，在求解该方程后容易得到原问题的解；

(2)根据判别式来构造相应的一元二次方程；

(3)根据韦达定理的形式构造相应的一元n次方程，在求解该方程后容易得到原问题的解；

(4)根据已有条件构造一元n次方程，利用韦达定理得到原问题的解，其中需利用变元与系数相互转化的思路.

总而言之，对于一些有技巧性或者有难度的题目，如果根据题目特征能构造相应方程，那么求解将会更加便捷，思路更加清晰.教师在日常教学中，可以引导学生进行构造方程解决问题的训练.这种训练不仅有助于学生构建数学知识间的关联，而且也是对学生数学解题能力、创新能力以及逆向思维、发散思维的锻炼.