考虑多时间尺度特征的电力系统稳定性界分析

马兆兴，秦昌民，朱文杰，钱宝珊

考虑多时间尺度特征的电力系统稳定性界分析

马兆兴，秦昌民，朱文杰，钱宝珊

(青岛理工大学信息与控制工程学院，山东 青岛 266520)

电力系统运行的稳定性常常与换流器的接入有关，而换流器装置的时间尺度与传统电力系统并不一致。在电力系统中，为揭示电力系统含有不同时间尺度装置对稳定性的相互影响，建立了稳定性界的计算分析方法。从换流器接入电力系统的角度入手，基于奇异摄动理论，建立了多时间尺度系统稳定性界的分析模型，给出了求取该系统稳定性界的理论方法，并进行了数学理论证明。通过Matlab时域仿真，进行了定量分析和验证。结果表明，计及快、慢变量所构建系统可以准确描述稳定性动态响应特性；奇异摄动分析可以精确刻画不同时间尺度变量构成的电力系统稳定性界。此外，数值仿真结果验证了所提模型和稳定性界分析方法的准确性。

奇异摄动；电力系统；稳定性界；多时间尺度；流形

0 引言

电力系统自大规模商业运营到现在，已超过一个世纪的时间，由于科学技术的快速发展和社会需求的不断进步，对电力系统的要求也在持续变化，期间经历了不同的形态演化。进入21世纪以来，环境保护的压力与日俱增，对电力系统提出了新的要求。在电网侧，可再生能源装机和并网容量发展迅速[1-4]，我国可再生能源的装机容量居世界第一，截至2019年底已达到1437 GW[5-6]，预计到2030年之前，我国光伏、风电的总装机容量将达到2 TW[7]；柔性交直流输电得以较大规模应用，截至2019年底，我国柔性交直流输电规模超过200 GW[8])；在用电侧，电动汽车、电能质量控制设备和变频传动设备等新型设备得以快速发展与普及，目前的变频设备容量已超过40 GW[9]；这些大多是通过电力电子设备接口并网，直接推动了电力电子设备在网络系统中的广泛应用，从而使得电力系统较以往呈现出明显的多时间尺度特征，这也逐渐成为新一代电力系统的重要特征，由此给电力系统的稳定性分析及稳定性运行带来新的问题和挑战[10-11]，对多时间尺度电力系统稳定性的研究变得极具意义和前瞻性。

现代电力系统中，新能源发电注入比例不断提升，直接加剧了新型电力电子变换设备的应用，随之电力系统稳定分析展现出明显的多时间尺度特征，该特征对系统可靠性、稳定性分析及运行产生极大影响。多时间尺度电力系统稳定性分析是一个更为复杂的研究课题，与现有电力系统中一般只考虑一个时间尺度的研究存在较大差异，主要表现在模型建立、稳定性分析理论、计算方法等。现有的电力系统稳定性分析方法，一般有直接法、间接法、智能化方法等[12-16]，如基于经典的李雅普诺夫稳定性分析、能量函数方法和一些智能化算法等，这些方法对解决和分析电力系统稳定性问题起到了非常重要的作用，但大多针对的是传统单一时间尺度的系统，而面对多时间尺度电力系统稳定性研究或许并不能完全适用，需要寻求更为有效的稳定性分析理论和计算方法。在电力系统分析及电力电子化方面，考虑多时间尺度特征的研究时间还不长，尚处于开始阶段，但在其他学科，已经取得了非常多的成果[17-18]，这些方法可以加以借鉴，应用于多时间尺度电力系统的稳定性研究。

就目前电力系统出现的高比例可再生能源发展趋势，文献[19]阐述了随之出现的稳定性问题，根据不同特征，提出了一些稳定性问题分类方法和研究框架，为后续的建模、分析理论的确立起到了指导作用。在考虑多时间尺度特征的基础上，文献[20]分析了含可再生能源电力系统的消纳问题，给出了提升优化运行的评估方案，该方案更符合实际运行工况，能够进一步提高短期、中长期的优化运行。在弱连接条件下，文献[21]分析了电压源型换流器接入电网的静态稳定性问题，文中讨论静态失稳机理，并就不同控制方法对静态失稳的影响进行研究。电力电子化设备的大规模应用会加剧电力系统稳定分析的复杂度，文献[22]阐述了电力系统的故障特性，较为全面地论述了一些变量在暂态过程中的变化特性，并就电力系统展现出多时间尺度特征下的保护原理和方法给出了新的分析和解释。

基于奇异摄动理论，本文提出了分析多时间尺度电力系统稳定性界问题的理论方法，以期提供一个有效的分析手段。所提理论分析方法仅适用于两个时间尺度的系统，具体地，本文给出了多时间尺度系统稳定性界的计算原理，并就相关原理进行了理论证明；然后，根据电力系统的多时间尺度特征构建系统分析模型，从而可以间接地计算原系统摄动小参数的稳定性界，由此得到整个多时间尺度电力系统的稳定性界；最后，将所提分析方法在不同工况下进行计算仿真以验证准确性和鲁棒性。

1 换流器模型分析

三相电压源型功率变换器(voltage source converter, VSC)能够实现交流与直流系统之间的功率转换，是电力系统的一种重要设备，其控制环路和控制电气量表现出明显的多时间尺度特征。具体而言，内环电流控制部分的响应速度快，外环直流电压控制部分、端电压控制部分和锁相环部分响应速度较慢，对于传统电力系统的故障分析，其保护动作反应时间，在该时间尺度下与换流器外环电压控制部分相当。因此本文分析过程中，将稳定性分析系统模型的时间尺度分为两个，即内环控制部分为快变量，外环控制部分和锁相环部分为慢变量。

1.1 内环控制部分

内环控制部分主要是内环电流控制[23-24]，其结构原理如图1所示。

图1 内环电流控制原理图

根据图1，动态方程表示为

1.2 外环控制部分

外环控制部分主要是外环电压控制，其原理如图2所示。

图2 外环电压控制原理图

根据图2，动态方程表示为

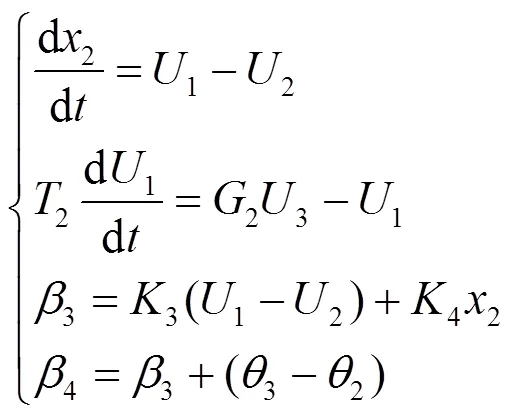
1.3 锁相环部分

锁相环的控制原理如图3所示。

图3 锁相环控制原理图

其状态空间模型表示为

2 多时间尺度系统稳定性界的分析

2.1 多时间尺度系统

奇异摄动理论广泛用于分析多时间尺度的微分系统，一般有频域和时域两种分析方法，它们基于的思想是相通的，将含多时间尺度系统描述为

2.2 系统稳定性界分析

矩阵与自身的bialnet加和用式(6)表示。

证毕。

证明过程同定理2。

3 电力系统稳定性界分析

现代电力系统稳定性分析中，呈现出明显的多时间尺度特征，所建立的系统分析模型有别于传统的微分-代数方程。根据第1部分的分析，若换流器接入电网，考虑换流器的多时间尺度特征，换流器内环控制部分为快变量，其他控制部分为慢变量，传统电力系统微分变量也为慢变量，共同建立起描述电力系统多时间尺度特征的数学模型，该多时间尺度电力系统模型表述为

由式(7)所建立的多时间尺度电力系统稳定性分析模型，由此计算平衡点处的雅克比矩阵，生成对应的含快、慢变量系统，即结合2.2节得到对应的矩阵1、2，然后应用bialnet乘积计算方法，得到矩阵0、0，继而分别计算1、2，得到min，由第2节所给定理判断系统稳定与否的界，即得到系统稳定性的界。其中1可看作奇异摄动小参数，研究1的范围，当1在稳定性界内变化时，可以保证系统为稳定的。

考虑多时间尺度特征，应用奇异摄动理论分析电力系统稳定性界的流程如图4所示。

4 数值算例分析

本文选择基准频率为60 Hz的不同系统作为测试电网。应用Matlab进行建模及仿真计算，在仿真计算过程中分多场景进行，以验证本文所提研究方法的正确性和鲁棒性。系统采用综合负荷，发电机出力根据负荷水平做出相应调整。换流器的参数详见表1。

图4 电力系统稳定性界分析流程图

表1 VSC控制器参数

为了说明文中所提稳定性界分析方法的有效性，本部分基于两种工况进行验证：一种为含换流器装备的简单系统；另一种为IEEE14节点多机系统。在第一种工况下，根据不同时间尺度换流器对稳定性界的影响，给出参数及取值计算结果。在第二种工况下，以IEEE14节点系统为基础，通过判断相互作用的多时间尺度特征换流器，给出系统稳定性界的计算及仿真结果，验证文中所提研究方法的适用性和鲁棒性。

4.1 系统一：简单系统分析

含换流器VSC的简单系统网络结构如图5所示，其中并网型VSC系统主要由控制部分和交流电网组成。VSC详细参数如表1所示。本节分析中，将VSC内环控制部分视为快变量，外环控制部分和锁相环部分为慢变量。

图5 并网VSC单机系统结构图

为体现文中所提理论分析方法的鲁棒性，在简单系统分析数值计算中分两种工况进行，分别为：工况一系统稳定运行；工况二为系统不稳定运行。

各工况条件下，系统详细运行状态描述如下。

4.1.1工况一

表2 系统部分特征值计算结果

图6 电压-时间变化间

4.1.2工况二

表3 系统部分特征值结果

表3的计算结果表明，系统雅克比矩阵有实部为正的特征值，是不稳定的。现进行节点电压的时域仿真计算，简单系统节点电压数值仿真曲线如图7所示。

图7 电压的时域曲线

4.2 系统二：多机系统分析

为进一步验证文中所提稳定性界分析方法在描述大规模电力系统中的适用性，本文扩大了案例系统的规模进行数值仿真验证，在Matlab中建立系统模型，案例拓扑结构如图8所示。

图8 IEEE14节点系统拓扑结构简图

在图8中，在节点3和节点4之间、节点6和节点13间分别设置为高压直流输电线路，现计算分析该系统稳定性界的问题。为体现文中所提理论分析方法的鲁棒性，数值计算中分两种工况进行，不同工况下的简要描述如表4所示。

表4 不同工况下的运行状态

各工况条件下，系统详细运行状态如下所述。

4.2.1工况一

表5 系统部分特征值结果

现进行节点电压的时域仿真计算，系统部分节点电压数值仿真曲线如图9所示。

图9 电压变化曲线

4.2.2工况二

表6 系统部分特征值结果

由表6计算结果知，系统是不稳定的。为进一步仿真验证系统节点电压变化，部分节点电压随时间变化趋势如图10所示。

图10 电压随时间变化趋

5 总结

本文提出一种考虑多时间尺度特征的电力系统稳定性界分析方法。首先，给出了含换流器的电力系统多时间尺度模型；其次，基于摄动理论，给出了多时间尺度系统稳定性界的理论分析方法及证明过程；最后，应用不同电力系统案例对所提分析方法进行数值计算验证，并分别在不同工况下进行了测试。通过本文的工作，得到如下结论：

1) 对于含有快、慢不同时间尺度的系统而言，不同时间尺度的变量间相互作用对整个系统的稳定性将产生较大影响，文中所提方法有效厘清了不同时间尺度系统的稳定界计算问题。

2) 针对多时间尺度电力系统，与忽略快变量的研究方法相比，本文所提方法能更全面地反映整个电力系统的稳定状态，可以更为详实地描述电力系统的动态特性。

3) 文中提出的稳定性界计算方法，理论清晰，计算过程简洁，为多时间尺度电力系统稳定性分析及动态性能预测提供了简便而实用的工具。

4) 本文所提方法对所研究的电力系统结构无特殊要求，可形成一种适用范围较广的两时间尺度系统稳定性界研究方法。

在后续研究中，将对含3个及以上多时间尺度的电力系统稳定性界问题做深入研究，并就含多时间尺度电力系统降阶的合理性条件做进一步探讨分析。

[1] MA Zhaoxing, JIA Hongjie, XIN Liping. Study on influence of various wind farm correlations on voltage stability with multidimensional data streams method[J]. Journal of the Chinese Institute of Engineers, 2019, 42(8): 738-747.

[2] CHEN Hao, LI Fangxing, WANG Yurong. Wind power forecasting based on outlier smooth transition autoregressive GARCH model[J]. Journal of Modern Power System and Clean Energy, 2018, 6(3): 532-539.

[3] 陈昊, 高山, 王玉荣, 等. 基于广义自回归条件异方差偏度峰度模型的风电功率预测方法[J]. 中国电机工程学报, 2017, 37(12): 3456-3461.

CHEN Hao, GAO Shan, WANG Yurong, et al. Wind power forecasting method based on generalized autoregressive conditional heteroskedasticity with skewness and kurtosis mode[J]. Proceedings of the CSEE, 2017, 37(12): 3456-3461.

[4] YIN Rui, LI Dengxuan, WANG Yifeng, et al. Forecasting method of monthly wind power generation based on climate model and long short-term memory neural network[J]. Global Energy Interconnection, 2020, 3(6): 571-576.

[5] REN21. Renewables 2020 global status report[R]. Paris: REN21, 2020.

[6] BADAL F R, DAS P, SARKER S K, et al. A survey on control issues in renewable energy integration and microgrid[J]. Protection and Control of Modern Power Systems, 2019, 4(1): 87-113.

[7] 国家发展和改革委员会能源研究所. China renewable energy outlook 2019[EB/OL]. [2020-05-20]. 北京: 可再生能源发展中心, 2019. https://www.dena.de/fileadmin/den.

[8] 中国南方电网有限责任公司超高压输电公司. 高压直流输电工程运行技术研究专题报告[R]. 广州: 中国南方电网, 2019.

[9] 袁小明, 程时杰, 胡家兵. 电力电子化电力系统多尺度电压功角动态稳定问题[J]. 中国电机工程学报, 2016, 36(19): 5145-5154.

YUAN Xiaoming, CHENG Shijie, HU Jiabing. Multi-time scale voltage and power angle dynamics in power electronics dominated large power systems[J]. Proceedings of the CSEE, 2016, 36(19): 5145-5154.

[10]杨子千, 马锐, 程时杰, 等. 电力电子化电力系统稳定的问题及挑战: 以暂态稳定比较为例[J]. 物理学报, 2020, 69(8): 1-14.

YANG Ziqian, MA Rui, CHENG Shijie, et al. Problems and challenges of power-electronic-based power system stability: a case study of transient stability comparison[J]. Acta Physica Sinica, 2020, 69(8): 1-14.

[11]陈垣, 张波, 谢帆, 等. 电力电子化电力系统多时间尺度建模与算法相关性研究进展[J]. 电力系统自动化, 2021, 45(15): 172-183.

CHEN Yuan, ZHANG Bo, XIE Fan, et al. Research progress of interrelationship between multi-time-scale modeling and algorithm of power-electronized power system[J]. Automation of Electric Power Systems, 2021, 45(15): 172-183.

[12]黄鹭鹭, 高波, 孙丽敬. 电网支持型变流器输出建模、控制及稳定性分析[J]. 电力系统保护与控制, 2022, 50(4): 44-53.

HUANG Lulu, GAO Bo, SUN Lijing. Analysis of modeling, control and stability for grid-supporting power converters[J]. Power System Protection and Control, 2022, 50(4): 44-53.

[13]马兆兴, 陈昊, 万秋兰. 计及SATACOM容量约束的电压失稳性分析[J]. 中国电机工程学报, 2013, 33(28): 88-93.

MA Zhaoxing, CHEN Hao, WAN Qiulan. Analysis on voltage instability considering STATCOM capacity constraint[J]. Proceedings of the CSEE, 2013, 33(28): 88-93.

[14]MA Zhaoxing, CHEN Hao, CHAI Yanli. Analysis of voltage stability uncertainty using stochastic response surface method related to wind farm correlation[J]. Protection and Control of Modern Power Systems, 2017, 2(4): 1-9.

[15] WANG Yi, ZHANG Ning, KANG Chongqing, et al. An efficient approach to power system uncertainty analysis with high-dimensional dependencies[J]. IEEE Transactions on Power Systems, 2018, 33(3): 2984-2994.

[16]康卓然, 张谦, 陈民权, 等. 适用于电力系统暂态稳定分析的网络电压解析算法研究[J]. 电力系统保护与控制, 2021, 49(3): 32-38.

KANG Zhuoran, ZHANG Qian, CHEN Minquan, et al. Research on network voltage analysis algorithm suitable for power system transient stability analysis[J]. Power System Protection and Control, 2021, 49(3): 32-38.

[17]BROUGHTON J Q, ABRAHAM F F, BERNSTEIN, et al. Concurrent coupling of length scales: methodology and application[J]. Physical Review B, 1999, 60(4): 2391-2403.

[18]WEINAN E. Principles of multiscale modeling[M]. Cambridge, England: Cambridge University Press, 2011.

[19]谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-474.

XIE Xiaorong, HE Jingbo, MAO Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power electronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-474.

[20]邵成成, 冯陈佳, 王雅楠, 等. 含大规模清洁能源电力系统的多时间尺度生产模拟[J]. 中国电机工程学报, 2020, 40(19): 6103-6112.

SHAO Chengcheng, FENG Chenjia, WANG Yanan, et al. Multiple time-scale production simulation of power system with large-scale renewable energy[J]. Proceedings of the CSEE, 2020, 40(19): 6103-6112.

[21]郑超航, 李华. 弱电网下电压源型变换器静态稳定性分析[J]. 电力系统保护与控制, 2021, 49(17): 38-47.

ZHENG Chaohang, LI Hua. Static stability analysis of voltage source converters connected to a weak grid[J]. Power System Protection and Control, 2021, 49(17): 38-47.

[22]郑博文, 王增平, 吕哲, 等. 基于暂态量的继电保护研究[J]. 电力系统保护与控制, 2020, 48(22): 18-25.

ZHENG Bowen, WANG Zengping, LÜ Zhe, et al. Research on transient-based relay protection[J]. Power System Protection and Control, 2020, 48(22): 18-25.

[23]叶运铭, 汪娟娟, 陈威, 等. 基于小干扰动态模型的LCC-HVDC系统控制器参数优化方法[J]. 南方电网技术, 2021, 15(4): 1-9.

YE Yunming, WANG Juanjuan, CHEN Wei, et al. Controller parameters optimization method for LCC-HVDC system based on small-interference dynamic model[J]. Southern Power System Technology, 2021, 15(4): 1-9.

[24]王旭斌, 杜文娟, 王海风. 弱连接条件下并网VSC系统稳定性分析研究综述[J]. 中国电机工程学报, 2018, 38(6): 1593-1604.

WANG Xubin, DU Wenjuan, WANG Haifeng. Stability analysis of grid-tied VSC systems under weak connection conditions[J]. Proceedings of the CSEE, 2018, 38(6): 1593-1604.

[25]LIU W Q, SREERAM V. A new characterization on stability bounds for singularity perturbed systems[J]. Elsevier Linear Algebra and Its Applications, 1997, 263: 377-388.

[26]CHEN B, LIN C. On the stability bounds of singularly perturbed systems[J]. IEEE Transactions on Automatic Control, 1993, 35: 302-304.

[27]KOKOTOVIC P V, KHALIL H K, REILLY J O. Singular perturbations methods in control: analysis and design[M]. New York: Academic Press, 1986.

Analysis of the stability bound of a power system considering multi-time scale characteristics

MA Zhaoxing, QIN Changmin, ZHU Wenjie, QIAN Baoshan

(School of Information and Control Engineering, Qingdao University of Technology, Qingdao 266520, China)

The stability of power system operation is often related to the access of the converter, and the time scale of a converter device is not consistent with the traditional power system. In order to reveal the interaction of stability occuring between devices with different time scales, a calculation and analysis method of a stability bound is established. This paper considers a converter connecting to a power system, and based on singular perturbation theory, establishes an analysis model of multi-time scale system stability bound. A theoretical method for obtaining the system stability bound is given, and the method is proved by mathematical theory. It uses Matlab time domain simulation to carry out quantitative analysis and verification. The results show that the system with fast and slow variables can accurately describe the stability and dynamic response characteristics. Singular perturbation analysis can accurately describe the stability bound of a power system composed of variables with different time scales. In addition, the numerical simulation results validate the accuracy of the proposed model and stability bound analysis method.

singular perturbation; power system; boundary of stability; multiple time scale; manifold

10.19783/j.cnki.pspc.220238

国家自然科学基金项目资助(61803220)；山东省自然科学基金面上项目资助(ZR2020ME194)

This work is supported by the National Natural Science Foundation of China (No. 61803220).

2022-02-27；

2021-05-23

马兆兴(1982—)，男，博士，讲师，硕士生导师，研究方向为电力系统分析、运行，综合能源系统；E-mail: mazhaoxing@qut.edu.cn

秦昌民(1997—)，男，硕士研究生，研究方向为电力系统小扰动稳定分析及控制；E-mail: Qin_changmin@126.com

朱文杰(1981—)，男，博士，副教授，硕士生导师，研究方向为电力电子技术。

(编辑 周金梅)