液流电池中碳布对电解液流动影响的试验及模拟

方长顺

(上海电气(安徽)储能科技有限公司,安徽省 巢湖市 238000)

0 引言

自工业革命以来,人类社会活动主要依赖于以煤炭、石油为代表的化石能源,随之而来的是因二氧化碳过度排放引起的温室效应和全球变暖。近年来,随着“碳达峰”“碳中和”的提出,风力发电、太阳能发电等新能源得到了快速发展[1-2]。但是新能源发电都普遍面临着不能对电网进行持续供电的问题,因此“双碳”目标的实现对大规模储能设施的配备提出了迫切需求[3-5]。

液流电池因其功率单元和容量单元可自由调配、安全无污染、适中的维护成本和长寿命循环,特别适用于大规模长时储能[6]。因此,对于液流电池的研究与讨论就有着相当重要的意义。

液流电池中电极一般为惰性材料,不参与化学反应,仅为电解液中的活性物质进行电化学反应提供场所。电解液经过流道进入电极,最后经流道流出,根据电解液在电极内的流动状态,电极可分为流通性电极和流经型电极。以碳毡为代表的流通型电极,孔隙率、渗透率、比表面积大,流动阻力小;以碳布为代表的流经型电极则与之相反[7]。

在液流电池中,作为电极的碳布,在双极板和板框的支撑下,电解液在碳布中流动扩散并发生电化学反应,从而进行充放电循环。相对于其他的储能技术路线,液流电池所用电解液能量密度较低,所需流量大,整堆的流动阻力也大,进而系统集成所需要的泵耗也越大,严重影响储能系统的整体效率[8]。

液流电池堆是由多片单电池串联并压缩固定到一起的,2块双极板之间的配合尺寸决定了碳布的压缩量,不同的压缩量对应不同的渗透率。碳布压缩量越大,渗透率越小,电解液的流动阻力越大,供应电解液流动所消耗的泵功也越大。

碳布本身性质和压缩状态为影响渗透率的主要因素,决定了单电池在一定流量下的流动状态。本文采用试验与模拟相结合的方法,研究液流电池中碳布压缩状态对电解液流动特性的影响。

1 试验研究

设计并搭建碳布渗透率测试工装及测试系统,碳布渗透率测试工装包括盖板、底板、密封圈、薄板、碳布,如图1所示。碳布渗透率测试系统包括碳布渗透率测试工装、储液罐、循环泵、压力表、量筒和计时工具,如图2所示。

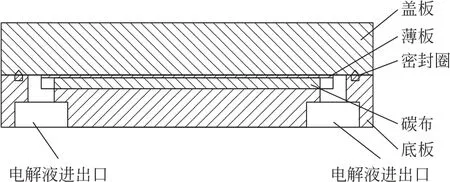
图1 碳布渗透率测试工装剖面图Fig.1 Cross-section view of carbon cloth permeability test tool

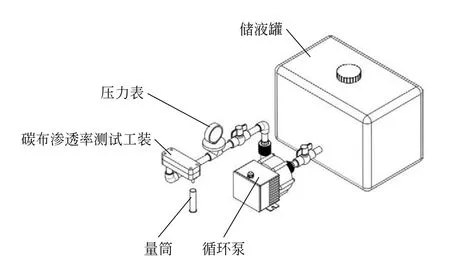
图2 碳布渗透率测试系统Fig.2 Carbon cloth permeability test system

碳布渗透率测试工装底板内凹槽深度为0.5 mm,用来放置碳布和薄板。碳布的原始厚度为0.6 mm,当薄板厚度为0.2 mm时,碳布压缩后的厚度为0.3 mm;当薄板厚度为0.1 mm时,碳布压缩后的厚度为0.4 mm;不放置薄板时,碳布压缩后的厚度为0.5 mm。通过放置薄板的厚度来调节碳布渗透率测试工装内待测碳布的压缩量。

循环泵将储液罐中的电解液送入碳布渗透率测试工装,电解液从工装任意一端进入,另一端流出。出口端有量筒、计时器,出口流出电极液时开始计时,量筒内达到一定体积电解液时停止计时。因此,可设量筒内电解液体积为x,计时器时间为t。在时间段t内,分3次记录压力传感器数值,并求平均值,设为ΔP。

通过可编程逻辑控制器(programmable logic controller,PLC)控制循环泵电机频率,从而改变循环泵的流量。每组试验分别测试了电机在35、40、45、50 Hz这4种频率运行下的渗透率相关数据。

假设碳布为均匀多孔介质,压降与流速的关系式[9-10]为

式中:Si为第i(x,y,z)方向的动量方程源项;vi为某点沿某方向流速;α为渗透率;C2为惯性阻力系数;μ为动力粘度;v为流速;ρ为电解液密度。

式中Δn为电解液流动方向上的长度。

本文分别测试了厚度为0.6 mm 的碳布被压缩至0.3、0.4、0.5 mm 这3种状态下的压降和流速。每种压缩状态下均测试4组数据,根据试验结果计算碳布渗透率、粘性阻力系数和惯性阻力系数,如表1所示。

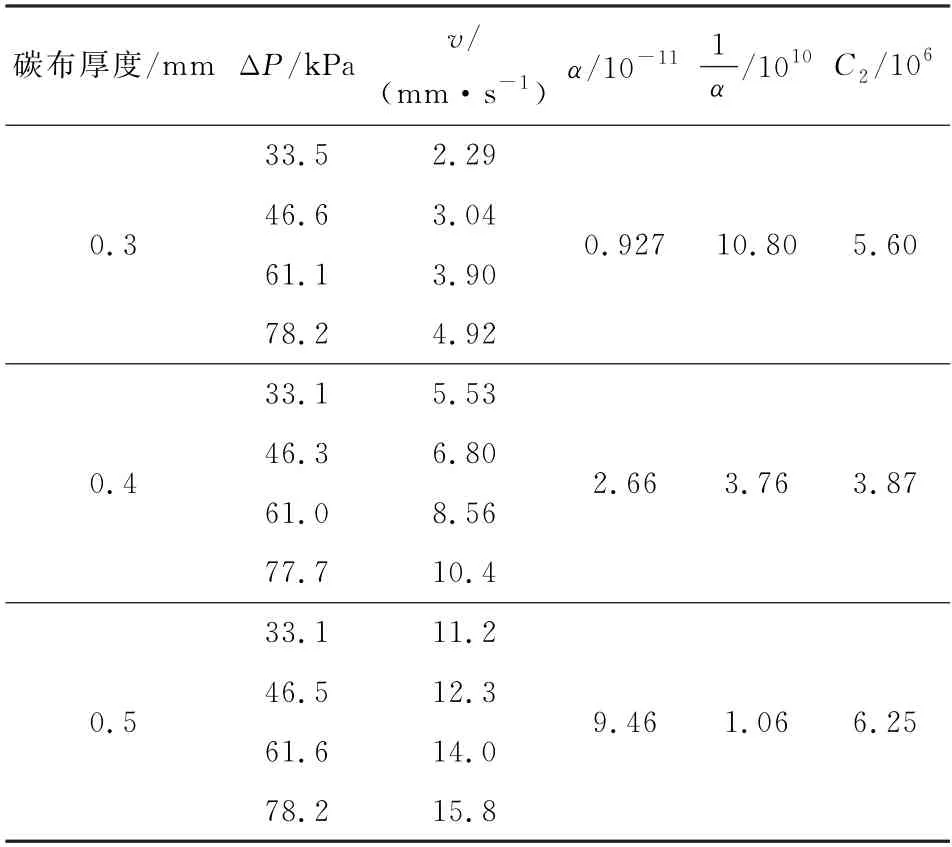
表1 试验数据及计算结果Table 1 Test data and calculation results

在试验中,随着压缩量的增大,压缩剩余量的减小,渗透率在逐渐减小。即在一定流量下,电解液通过碳布的压降逐渐增大,如图3所示。这是因为一定厚度的碳布逐渐被压缩,碳布内部的纤维结构变得逐渐密集,孔隙率更小,电解液更难以从内部流过。

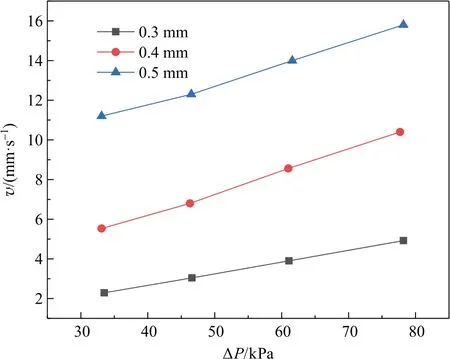
图3 试验中压降-流速变化趋势Fig.3 Variation trend of pressure drop-flow velocity in the test

因此,在相同流量下,压缩量越大,压降越大,消耗的泵功越大;或者说,消耗相同的泵功,压缩量越大,所能提供的电解液流量也就越小,传质效率降低,浓差极化增大,这对于液流电池内部电解液的流动是十分不利的。另外,压降越大,电堆在生产过程中对外密封的要求也越高。

2 数值模拟

泵功损失计算公式为

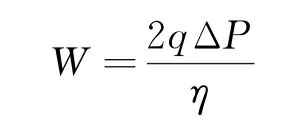
式中:q为流量;η为泵效率[11]。

因此,在相同泵功损失下尽可能地增大流量而减小压降成为液流电池内部流场设计的重要任务。

主流的方法是在双极板两侧雕刻流道,碳布位于双极板两侧,以增加流道的方式来减小电解液在电堆内的流动阻力[12-14]。现有技术中,应用最广的2种流道设计分别是叉指型流场和蛇形流场。然而,YOU 等试验发现,蛇形流道中电解液只有在较高的流量下消耗较大的泵功率,才会显示较好的性能[15]。

叉指形流道中电解液进出流道之间互不联通,电解液从进液流道溢出,流经碳布,再进入出液流道,如此增大了碳布上电解液的强制对流,尤其在较高的电流密度下,叉指形流道的电化学性能更优于蛇形流道[16-19]。

因此,本文通过数值模拟的方法研究了叉指形流场结构中电解液的流动特性,如图4所示。双极板长500 mm、宽400 mm,流道截面积为6×6 mm2。

图4 单电池中双极板与正负极电极(碳布)Fig.4 Bipolar plate and positive and negative electrodes (carbon cloth)in a single cell

以上文中试验计算得出的渗透率、粘性阻力系数和惯性阻力系数为基础,分析了电堆中流道及碳布的整体流动状态。计算模型分为流道和碳布(多孔介质)2部分,其中碳布的粘性阻力系数和惯性阻力系数取自试验计算结果。

2.1 几何模型与网格划分

单电池正负极流道和碳布所构成的流体域结构对称,截取正极流体域如图5所示。正极流体域中,进出液流道成对称结构,且尺寸一致,因此截取其中的1个最小单元进行模拟,几何模型如图6所示;并对该最小单元流体域划分网格,如图7所示。

图5 单电池正极流体域Fig.5 Anode fluid domain of single cell

图6 最小单元流体域Fig.6 Minimum unit fluid domain

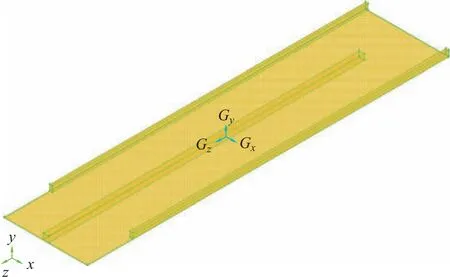
图7 最小单元流体域网格划分Fig.7 Meshing of minimum element fluid domain

2.2 网格无关性验证

以碳布压缩后厚度0.5 mm 模型划分网格,网格数量从937 600增加到1 556 875,再增加到2 974 620。设置4组不同流量的边界条件,其余条件完全一致,压降ΔP和电极平均流速v的变化率不超过1%,如表2所示。在保证计算精度的情况下节省计算资源,在后续计算中选用第1种网格数量。

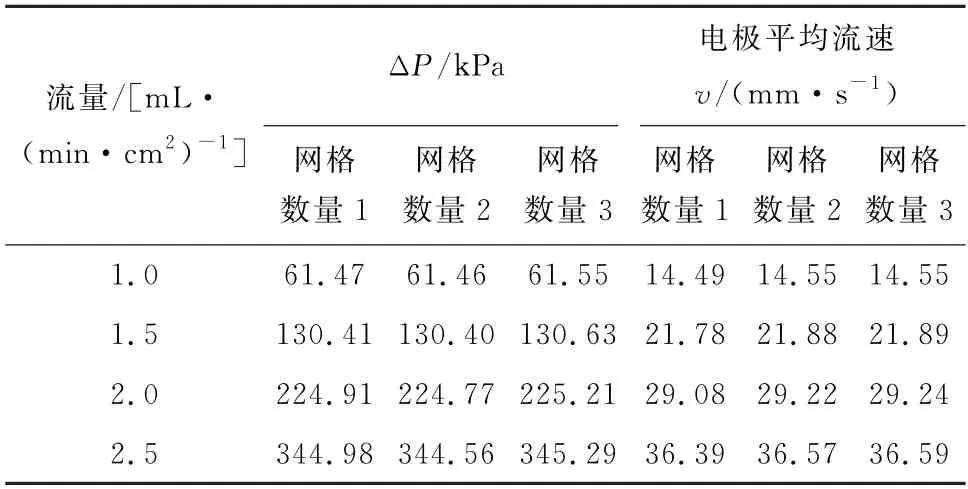
表2 网格无关性验证Table 2 Grid independence verification

2.3 模拟结果

电解液密度为1 400 kg/m3,动力粘度为0.001 3 Pa·s。分别计算了碳布厚度为0.3、0.4和0.5 mm 的模型在不同流量下的压降和电极平均流速,计算结果如表3所示。

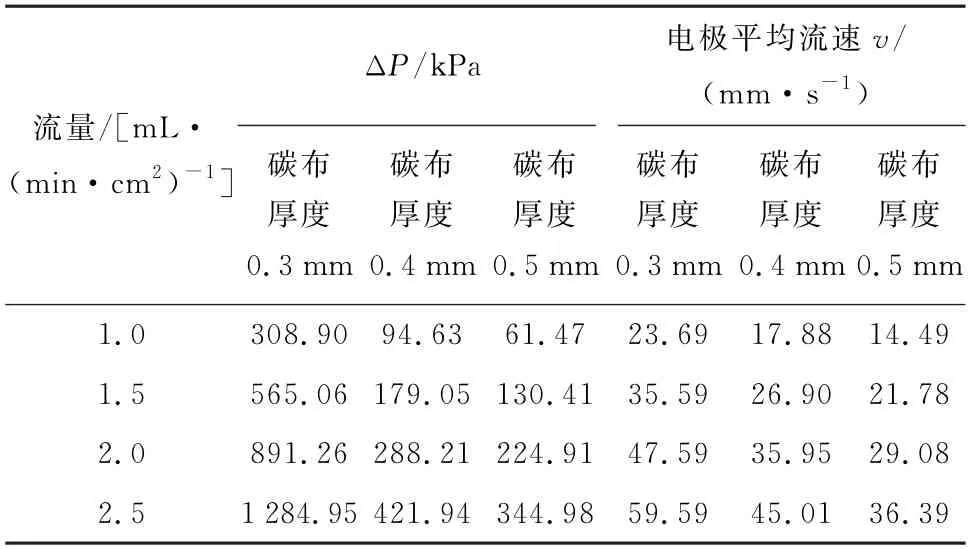
表3 数值模拟结果Table 3 Numerical simulation results

压降和电极平均流速随流量变化趋势如图8所示,由图8可看出,随着流量增大,计算压降和平均流速都在逐渐增大。碳布压缩量相同,流量增大,流速增大,电解液沿程阻力和局部阻力也逐渐增大。压缩量增大,碳布的内部结构发生变化,孔隙率降低,压降增大,维持一定流量所消耗的泵功增大。

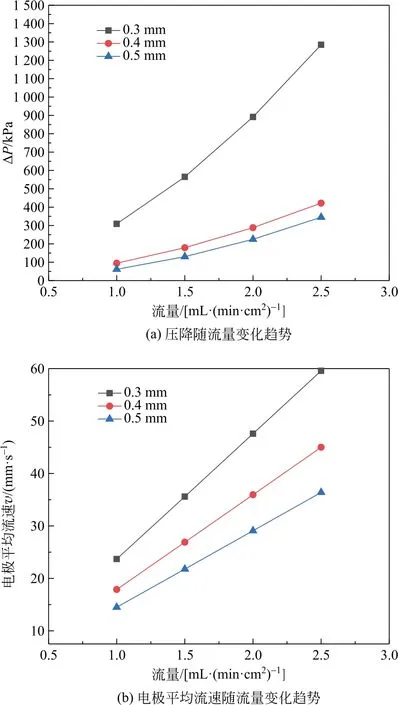
图8 压降和电极平均流速随流量变化趋势Fig.8 Variation trend of pressure drop and electrode average flow rate with flow rate

3 结果与讨论

双极板上雕刻的各条进液流道(或出液流道)之间在结构上属于并列关系,电解液首先完全充满各条进液流道,然后在压力作用下从进液流道溢出,流经电极,汇聚进入各条出液流道。因此,1条进液流道和2个半条出液流道的流场结构,构成了1个最小的计算单元。单电池整体流场正是由若干个最小计算单元组成,且各计算单元之间为并联关系,类似1个并联管路系统。根据流体力学中并联管路总压降等于各支路压降的基本原理,选取1个单元进行计算,简易可靠且满足计算流体动力学计算的经济性。

对电解液在进出液流道和碳布处的流动状态进行可视化处理,选取了碳布压缩剩余量为0.5 mm,不同流量下的压力云图和速度云图进行分析,如图9所示。其他条件下的模拟结果,流场规律亦如此。

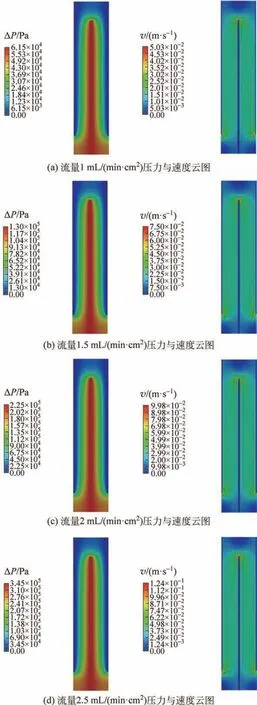
图9 0.5 mm 厚碳布在不同流量下的压力和速度云图Fig.9 Pressure and velocity nephograms of 0.5 mm thick carbon cloth under different flow rates

从压力云图中可看到,电解液在进液流道中的压力是最大的,出液流道的压力是最小的,电解液在流道内主要受到沿程阻力损失和局部阻力损失,进液流道内的电解液溢出流经碳布,压力迅速降低,最终汇入出液流道流出。除去流道的碳布部分,是流场中压力梯度最大的区域,该部分电解液主要受到碳布作为多孔介质所带来的流动阻力。

从速度云图中可看到,进出液流道是电解液流速最小的区域。进液流道处的碳布下表面首先与电解液接触,进而流道处的碳布处于一种浸泡的状态,进一步电解液从该处碳布两侧分别向出液流道流动。电解液从出液流道处碳布的两侧流入,压力和速度急剧减小,并汇聚流出。双极板正负极流道上下对称,与流道接触的碳布基本处于原始厚度状态,而其余部分碳布处于特定压缩状态,通流截面积最小,因此流量一定时,该区域碳布速度最大。

电解液在电堆内部流动过程中,流道和流道末尾处的速度最小,与碳布其他区域形成相对死区,该处电解液较其他区域传质效率较低,电流密度较小,电压分布不均,影响单电池以及电堆性能的一致性。因此,适当减小流道的数量和尺寸有利于电解液在碳布上的均匀分布,减小电解液流动死区。

4 结论

(1) 设计并搭建了液流电池用电极渗透率测试平台,试验了碳布在不同压缩状态和不同流量下的流动状态,并根据试验数据计算了碳布相关数值。该测试方案和计算方法不仅适用于碳布,同时也适用于液流电池用其他类型的电极。

(2) 液流电池内部电解液流动阻力主要来源于压缩状态下的碳布。随着碳布压缩量增大,电解液维持一定流量的流动阻力增大,并且在后期流动阻力呈现急剧上升的趋势。因此,液流电池在整体设计中应考虑,在保证电化学性能的同时,尽可能地减小电极压缩量,进而降低泵功损失,提高储能系统效率。

(3) 通过试验计算出特定压缩状态下多孔介质的渗透率、粘性阻力系数和惯性阻力系数,根据试验中的计算值并结合数值模拟,可以对现有的液流电池流场结构的流动阻力和流动状态进行初步分析,进而指导并修正设计方案。