基于Lambda算法的配电网故障定位方法研究

韦翔，梁艳，郭立，张丹，贾雅君

(1. 国网乌鲁木齐供电公司，乌鲁木齐 830011； 2. 上海交通大学，上海 200240 )

0 引 言

随着我国经济实力的飞速发展，无论是工业还是居民都对电力系统的稳定和可靠供应提出了更高的要求[1]。为了面对当前新形势下的各种具有挑战性的需求，我国电力传输和供应系统的建设和维护日益复杂。如何确保供电系统的可靠性、稳定性以及保持电力的高效传输逐渐成为当前的一个热门的研究课题[2]。

配电网作为终端用户和电力负荷中心之间的纽带，是整个电力供应系统中最重要的部分之一，作为向终端用户输送电力的主要通道，该网络的稳定性和安全性将直接对终端用户产生重大的影响[3]。配电网一旦出现故障将严重影响到正常的社会运转，导致严重的经济损失。对配电网故障精准定位是电力供应系统快速恢复的前提，因此配电网故障分析和定位等相关方面的研究在学术领域和经济领域都具有非常重要的价值和意义。随着风力、水利等高效清洁的分布式电源(Distributed Generation, DG)的大量使用，配电网结构由原始的单电源辐射式供电网络逐步转换为多电源分布式供电网络，导致配电网故障定位的难度迅速增加，传统的故障分析和定位方法在分布的拓扑网络结构下已不再适用[4]。

通过对配电网中馈线终端(Feeder Terminal Unit, FTU)上传的数据进行分析并完成故障的区段定位，是目前常用的一种配电网故障分析和定位方法。基于FTU故障分析和定位算法简洁高效、普适性强，并且可以根据不同的应用场景选择适当的数据处理方法如深度神经网络[5]、蜂群算法[6]、粒子群算法等[7]。文献[7]对经典的PSO算法进行了改进提出了一种适用于配电网故障定位的粒子群算法，这种在定位分析的过程中利用配电网络的拓扑关系来优化故障定位的精度，可以明显的加速数据分析过程，但是该方法在训练过程中不易收敛，容易陷入到局部最优解。文献[8]提出了一种基于矩阵相似度搜索的配电网故障定位算法，这种算法运算速度快、实时性强，可以完成配电网故障的快速定位，但是该方法鲁棒性差，对噪声数据非常敏感，一旦数据出现偏差，会导致故障定位精度明显下降。文献[9]提出了一种基于改进蝙蝠算法的配电网故障分析和定位技术，该算法针对传统的蝙蝠故障定位算法求解速度慢、精度低等问题，通过引入一种时变惯性权重因子来提高模型的收敛速度和对配电网故障的定位精度，该方法适用于故障量较少的情况，一旦故障数量超过一定阈值并且含有畸变时，该算法的性能会迅速下降。文献[10]提出了一种基于量子计算和免疫算法的配电网故障定位方法，该方法将量子计算的思想应用到缩减免疫算法的种群规模上，优化了免疫算法在克隆和变异过程中的全局搜索性能，有效的提高了算法收敛速度和全局故障寻优能力，但是量子计算存在建模复杂等缺点，导致该方法不能很好的适应具有多重故障且含有畸变信息的情况，并且算法的容错性能相对较差。

Lambda算法又被称为最小二乘模糊度去相关算法，是一种应用广泛的周期模糊度求解过程[11]。该方法自从被提出以来，因为其自身在求解整周期模糊度问题上效率和准确性，迅速成为学术界研究的焦点。针对目前基于智能算法的配电网故障定位技术存在的收敛速度慢、易于陷入局部最优解、全局搜索能力弱以及容错性差等缺点，文中将Lambda算法引入到配电网故障定位算法中，通过调整Lambda算法的Z变换方式来正则化模糊度搜索空间，进而提升算法的全局效率和故障定位精度。此外，文中还设计了多种配电网故障实验，证明了所提出算法的有效性和鲁棒性。

1 配电网故障定位的数学模型

1.1 配电网故障状态编码

传统的单一电源配电网中，一般采用0-1编码来表示该节点通过电流的状态和FTU的故障情况，其中节点区段状态正常使用0表示，节点发生故障使用1表示[12]。随着分布式电源(DG)逐渐接入到现有的配电网中，配电网的拓扑结构由原有的点状结构变为现在的发散状结构，并且潮流分布也发生的重大的变化，使原有的0-1故障编码无法适用于当前的配电网。在含有DG的配电网中，由于流经开关的故障电流方向具有不确定性，因此采用全新的编码方式来描述在含有DG的配电网中故障电流的方向。文中以系统电源指向负荷的方向作为故障电流的正方向，故障状态如式(1)所示。其中Ii表示流经第i个开关的电流方向。

(1)

1.2 开关函数

开关函数在配电网故障分析和定位问题中主要用来表示开关状态和FTU之间的关系，使用智能算法对FTU上传数据进行分析和定位时，其中一个关键的步骤是建立开关函数和配电网故障之间的相互对应关系[10]。由于含有DG的配电网的拓扑结构复杂程度远高于传统的单一电源的配电网，并且含有DG的配电网中，每一个开关处的故障电流的状态会受到相互关联的电源的影响。因此，文中对带有DG的配电网中的开关函数进行了重新定义，如式(2)所示：

(2)

1.3 适应度函数

使用智能算法对配电网故障进行定位时，构建恰当的适应度函数是其中最关键的一个步骤，适应度函数会对故障定位算法求解的精度和稳定性产生重要的影响[13]。在算法中，适应度函数用来关联和协调开关函数和开关处的电流阶跃状态，适应度函数的数值的大小表示故障定位的精度，精度越高函数值越小。因为含有DG的分布式配电网络复杂度高，使用传统的适应度函数可能会导致多个解的情况出现，因此文中借鉴“最小值理论[14]”，对传统的适应度函数进行修改，通过构建馈线故障电流Ij和分段开关函数之间的关系，来反映所有关联的馈线区间的状态，因此构建了一种具有容错能力的适应度函数，如式(3)所示：

(3)

式中Ij表示第j个开关处故障电流的阶跃状态；M表示配电网中开关的总数量；xi值FTU的实时状态；u是一个正则化参数，在实验中u=0.5。

2 Lambda配电网故障定位算法

2.1 Lambda算法求解过程

Lambda算法是一种采用最小二乘模糊度去相关调整算法[15]，该算法的核心是去相关和最小二乘搜索，其中去相关的过程主要是通过整数的Z变换算法来实现。Lambda算法主要是通过改变搜索空间的形状来提升搜索的效率和精度，该方法经过不断的发展和完善，目前已经具有了完善的理论体系和求解过程，在模糊度求解领域，是一种比较高效的运算方法[16]。Lambda算法的数学模型一般如式(4)所示：

y=Aa+Bb+e

(4)

式中y是观测模型；A、B分别是模糊度向量;e是双差模式下的误差观测向量；a和b需要在算法中进行求解向量，此时模型的基线约束可以看成是一个多维的球面。

为了对Lambda算法的数学模型进行求解，首先需要使用最小二乘法对式(4)进行求解，此时可以等价的转化为一个基于二次型约束条件下的最小二乘法的极值问题。获得a和b的协方差矩阵和整数解，首先需要对该模型进行正交分解，然后对协方差矩阵进行处理和模糊度求解[17-20]。因为a和b整数解和相应的协方差矩阵具有极强的关联性，会导致算法的搜索空间呈现出一种椭球形的状态，这种类型的搜索空间将会极大地影响算法的搜索效率。为了解决Lambda算法在某些特定情况下搜索效率较差的问题，因此需要在进行空间搜索之前，完成对协方差矩阵的Z变化，用来正则化搜索空间，Z变换一般使用式(5)来表示：

z=ZTa

(5)

一般来说，可以使用Z变换的模糊度矩阵必须要满足以下几个条件，分别是：

(1)模糊度矩阵中的元素数量需要是整数；

(2)变换前后的模糊度体积保持不变；

(3)变化后协方差矩阵相关性降低；

(4)变换后模糊度方程的乘积降低。

基于上述的4个条件，算法使用高斯变换构造出Z变化矩阵，经过变换之后的矩阵不再是原有的形状，因为在变化过程中对原有模型添加了基线长度的约束，使模糊搜索空间更加适用于实际使用，提升搜索的效率和精度。

2.2 Lambda算法模糊度搜索

经过Z变化后，原始的模糊度空间变成了一个具有N维空间的超椭球空间，该空间的中心是第N-1维度中的Z向量，Lambda算法将会在该模糊度空间中对所有可能的整数解进行搜索。算法在搜索空间中按照数据的大小进行搜索，并且每次只寻找一个整数解，一旦第i维空间中的解确定，算法将按照同样的方式对i-1维度进行搜索。经过有限次的迭代循环，如果可以在第1维空间中找到整数解，则可以确定整个周期的模糊度矢量。在实际使用场景中，可以通过多次搜索的方式来提升算法的搜索精度。

2.3 亲和度函数

亲和度函数是一种在配电网故障分析中常用的一种指标。使用智能算法在进行故障全局搜索的过程中，为了提高算法的效率，防止过拟合，可以利用亲和度函数对目标函数进行优化，亲和度的值一般在0-1之间。文中使用式(6)构建亲和度函数：

(6)

2.4 故障定位流程

进行配电网故障定位时，首先需要分析FTU所上传的数据，然后进行配电网故障区域定位，进而根据区域返回的状态码，确定故障的具体区段。基于Lambda算法的配电网故障定位流程如下：

(1)初始化Lambda算法，确定最小二乘法以及Z变换等参数；

(2)根据FTU所上传的故障数据信息，首先使用Z变换进行降维，对降维之后的数据进行去相关度搜索，同时使用亲和度函数作为损失函数，对小区域中的每一个节点的亲和度进行计算；

(3)记录最优的亲和度，作为算法下一次迭代的初始信息；

(4)重复步骤(2)～步骤(3)，直到算法收敛，将最后一次输出的信息作为算法的最优解，也就是配电网故障所在的位置。

3 算法仿真和案例分析

为了证明所提出算法的有效性和可靠性，文中构建出一种含有DG的配电网模型，使用MATLAB 2017b构建仿真开发环境，在Intel E5 3.1 GHz CPU、16 GB RAM的PC机上模拟配电网故障分析和定位。在基于Lambda配电网故障定位算法中，选择Z变换最小二乘法，基线长度默认为1。

3.1 单节点故障分析

为了证明所提出算法的有效性，因此设计了一个含有多个节点的配电网故障模型，该故障模型可以模拟单接点故障和多节点故障。首先对单节点配电网故障定位进行模拟实验，图1是具体的实验框图。当FTU上传的数据包含故障信息时，所提出的算法可以对关联信息进行分析来迅速确定故障的位置，具体分析结果如表1所示。

图1 含DG的配电网实验结构图

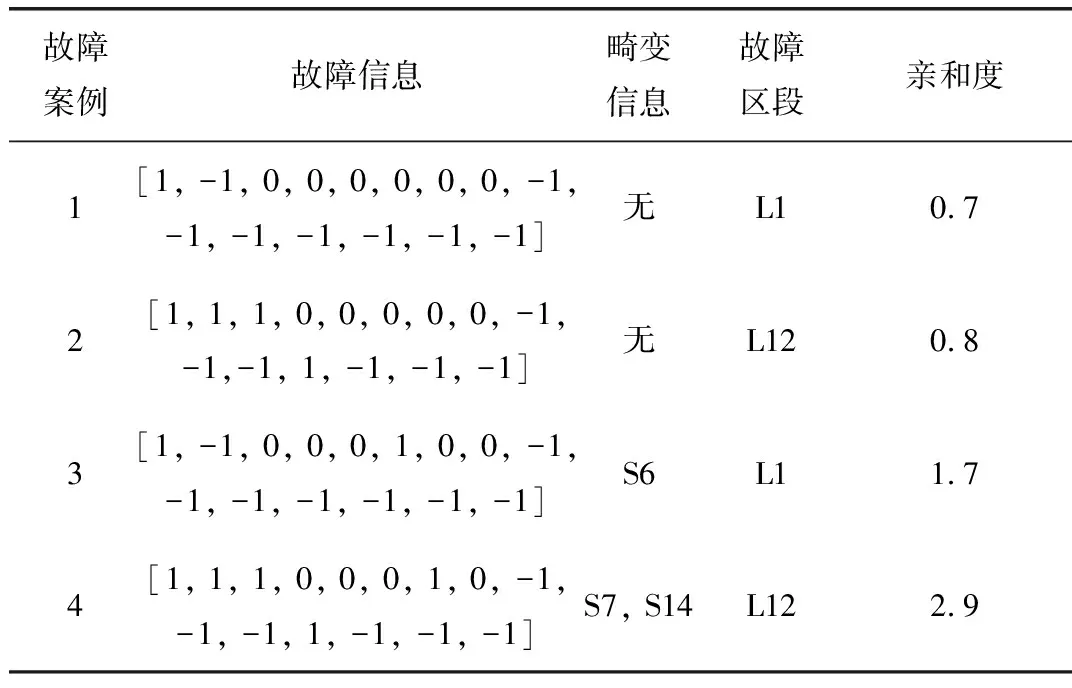
表1 配电网单节点故障定位结果

经过分析，由故障案例1和故障案例2可知，当配电系统发生单节点故障时，使用所提出的算法可以准确地完成故障区段的定位；故障案例3和故障案例4说明，所提出的算法具有较好的容错能力，当配电网中部分FTU发生故障时，算法仍然可以准确的定位到故障发生的位置。

3.2 多节点故障分析

随着目前供电系统的拓扑网络结构日益复杂，配电网在实际运行过程中经常会有多节点同时发生故障的情况产生，因此在仿真实验中使用图1的配电网模型模拟两处故障同时发生的情况。具体实验分析结果如表2所示。

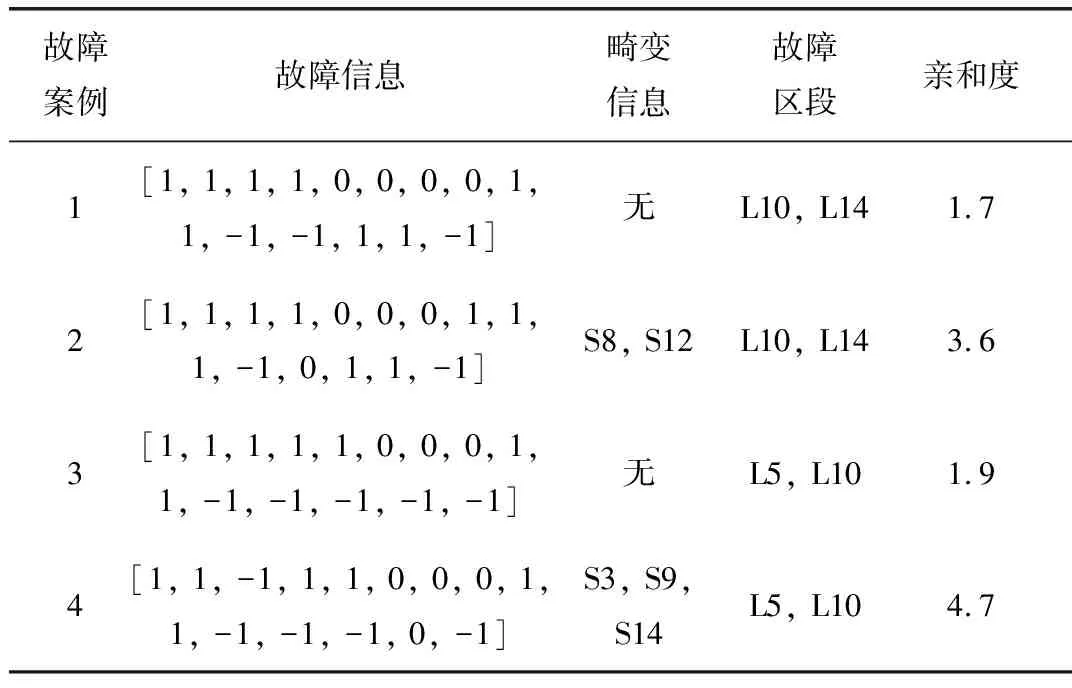
表2 配电网多节点故障定位结果

由表2的分析结果可知，所提出的算法在配电网多节点故障的情况下仍然可以有效地完成故障定位；同时故障案例2和故障案例4说明，算法在处理了多节点故障的时候具有较强的容错能力，也反映出了文中所提出算法具有很强的普适性和实际应用价值。

3.3 与基于智能算法性能进行比较

为了证明所提出的基于Lambda算法在配电网故障分析和定位问题上的性能，设计实验与常用的基于智能算法的配电网故障定位技术进行对比试验。以3.1节中单节点故障分析为例，对所提出的算法和经典的蚁群算法(ACO)在收敛频次、定位精度等方面进行对比分析，实验分析中，分别将每种算法运行50次，然后对结果进行统计。图2是两种算法迭代次数之间的对比，表3是两种算法的统计数据。同时使用ACO算法分析3.2中的过节点故障的部分多节点故障案例，具体对比结果如表4所示。

图2 算法收敛性能对比

表3 算法性能对比

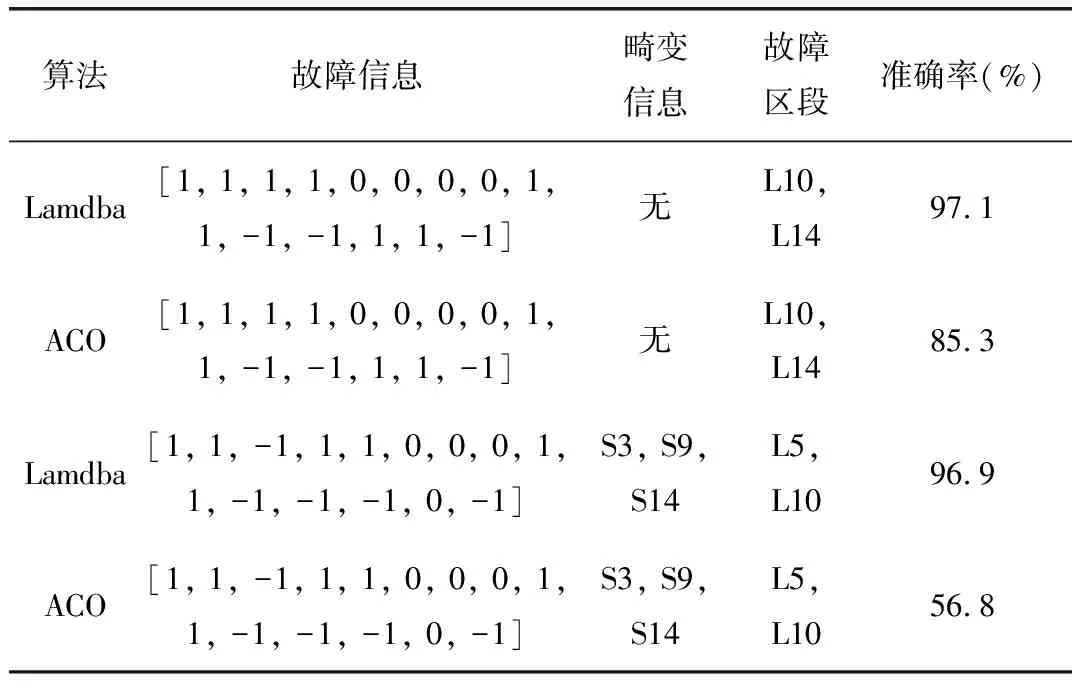
表4 两种算法在多节点故障定位中性能对比

从图2可以看出，所提出的算法收敛非常迅速，经过6次迭代之后模型基本收敛，但是ACO算法需要35次迭代后才能完全收敛。这一结果也从侧面说明了所提出的算法在搜索空间上的高效性。从表3的对比中，我们可以发现所提出的算法在迭代次数、准确率等指标上均大幅超越ACO算法，并且在运行时间上相比ACO算法提升了接近40%。此外，从表4中可以看出，所提出的Lamdba算法在含有DG的配电网中，无论是否含有信号畸变，算法的性能基本不会受到影响。但是ACO算法在含有DG的配电网故障分析中，一旦网络中包含畸变信号，定位的准确性将急剧下降，经过分析发现，ACO算法容易对L10区段的故障进行误判，但是文中所提的Lamdba算法不存在这一问题。

4 结束语

文中提出了一种基于Lambda算法的配电网故障定位算法，通过对经典的Lambda算法进行改进和优化，使算法可以更好地利用基线长度这一先验知识，同时使用Z变化来对模糊度搜索空间进行正则化，并且通过使用部分模糊度搜索算法来降低搜索空间的维度，有效地提升了算法在模糊度空间上搜索的效率和准确率。根据目前常用的配电网拓扑结构，分别设计了单故障定位实验和多故障定位实验，两组实验结果证明，所提出的算法可以准确、快速地对配电网中的故障进行分析和定位；同时进行了含有畸变信息的配电网故障定位实验，实验结果说明了所述算法具有很好的容错性能。此外，将所提出的算法和经典的蚁群算法进行对比，对比结果显示所提出的算法在故障定位精度、收敛速度等指标上均优于目前常用的智能算法，是一种实时性强、普适度高的配电网故障定位算法。