基于主导不稳定平衡点法的暂态电压稳定性研究

杜兆斌，黄昌树，陈智颖，詹富均，张文倩

(1. 华南理工大学，广州 510640； 2. 广东电网有限公司潮州供电局，广东 潮州 521000)

0 引 言

近年来，随着电力系统负荷的增加，电力系统的暂态电压失稳事故也时有发生[1-4]，引起了电气领域众多学者的关注。暂态电压失稳是源网荷特性共同作用的结果。CIGRE将电压稳定定义为：给定运行点的电力系统在经受某一给定扰动后，负荷附近的电压趋于扰动后稳定平衡点的值,它对应于扰动后系统状态在扰动后平衡点的吸引域中[5]。以上所提定义已经得到了广泛的认可与采纳。

目前，暂态电压稳定的分析手段仍然主要依赖于时域仿真法[6-7]。时域仿真法的模型适应性强，可以再现事故期间各个系统元件的动作顺序以及其对系统暂态稳定性的影响，便于系统稳定机理分析[8]。但其耗时较长，难以获取系统稳定性程度的定量指标[9]。作为时域仿真法的重要补充，能量函数法在近20年取得了重大的研究进展。主要包括主导不稳定平衡点(CUEP)法、势能边界面法等[10-11]。其中，CUEP法为精度较高的一种，使用与CUEP相切的恒能量面来近似系统的稳定域边界，该方法的成功应用取决于能否找到正确的CUEP。目前，已经提出很多计算CUEP的方法，如MOD法和BCU法[12-13]。当迭代初值充分靠近CUEP时，这些基于牛顿法原理计算平衡点的方法可以快速得到CUEP，但是，牛顿法对初值的要求较高，当初值落在牛顿法收敛域之外时，迭代可能发散或收敛到其他平衡点。文献[14]提出一种启发式的方法用于确定电压型CUEP的迭代初值，并采用牛顿法迭代得到主导不稳定平衡点，该方法操作简单，计算量少，但是牛顿法对初值比较敏感。数值结果也表明，在牛顿法下，电力系统模型的稳定平衡点和不稳定平衡点的收敛域均具有分形边界，分形边界的影响在于初值的微小变化将导致收敛于不同的平衡解[10]。而牛顿同伦法的收敛域是连通的[15]，比牛顿法有更好的收敛性[16]，可以有效克服牛顿法对初值的敏感性。故文章使用牛顿同伦法替代牛顿法，减弱了牛顿法下电力系统模型不稳定平衡点的收敛域分形边界影响，提高了数值计算收敛到电压型CUEP的可靠性，算例也验证了其可行性。

文章首先采用一种启发式的方法去寻找计算电压型CUEP的迭代初值，其中采用一种基于大干扰的电压幅值变化率指标来识别主导负荷母线，有别于文献[14]的小干扰电压稳定指标，更加充分考虑了暂态过程中的信息和系统非线性因素，可拓展到多电动机的动态负荷模型，提升了该启发式方法的模型适用性与推广性。然后引入牛顿同伦法求解非线性方程组，使得到的迭代初值更可靠地收敛到电压型CUEP，弥补了牛顿法对初值敏感的不足。在结合能量函数和得到电压型CUEP后，可以有效计算维持电力系统暂态电压稳定的临界切除时间。最后在3机9母线系统上验证了上述方法的有效性。

1 主导不稳定平衡点法的理论基础

电力系统的部分稳定域边界由稳定域边界上的不稳定平衡点(UEP)的稳定流形构成[10-11]，当发生暂态失穏时，系统的故障中投影轨迹穿过主导不稳定平衡点的稳定流形[17]。数学上难以求得稳定域边界的解析解，主导不稳定平衡点法把CUEP的能量作为临界能量，用临界能量构造一恒能量面，将该恒能量面作为稳定域边界的局部近似。以电力系统暂态稳定分析为例，当故障后初始能量小于临界能量时，意味着系统故障后初始状态落在稳定域内，则系统暂态稳定，反之，系统可能暂态失稳[11]。文献[18]提出电压稳定和功角稳定关系研究的统一能量函数法框架，指出功角失稳是由于故障轨迹穿过功角型UEP的稳定流形，而电压失稳是由于故障轨迹穿过电压型UEP的稳定流形，其中功角型UEP具有高电压、大功角的特点，电压型UEP具有低电压、小功角的特点。在此基础上，文献[19]在一个2机3节点系统中，详细考察了发电机出力大小、负荷大小和负荷模型对平衡点分布变化的影响，指出可以通过UEP的分布、数目和类型了解系统可能发生的暂态失稳模式，通过这些分析进一步支持了文献[18]的观点。因此，在能量函数法的思想下，功角稳定问题和电压稳定问题在状态空间上可以认为是UEP处于不同模式下的系统稳定问题[19-20]。

文章采用启发式方法求出电动机滑差的初值并代入UEP的求解中，使最终所得的UEP符合低电压、小功角的特点，因而文中所用主导不稳定平衡点法是针对暂态电压稳定的，这是文章与传统能量函数法求解暂态功角稳定域文献的不同之处。文章结合电动机特性及其与电压稳定的关系，以启发式的方法筛选合适的电压型UEP初值，为能量函数法切入暂态电压稳定性分析领域提供了一定的基础条件。从另一个角度看，也扩展了能量函数法运用于暂态稳定性分析的适用范围。

2 电压稳定域边界主导不稳定平衡点的求取

对于主导不稳定平衡点的求取，即求解故障后系统的方程，表达式如下所示：

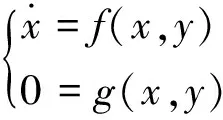
(1)

式中f为电力系统中的微分方程组，表示发电机、负荷的动态特性等；g为电力系统中的代数方程组，表示网络潮流约束；x表示电力系统的状态变量，如发电机功角、感应电动机滑差等；y表示电力系统的代数变量，如节点电压的幅值和相角等。以上方程组可以通过牛顿法进行求解，然而，迭代的初值选取是一个难题，因为如果选择不当，牛顿法迭代后有可能收敛到其它的不稳定平衡点。

文献[14]提出了一种启发式的方法用于求取电力系统电压型主导不稳定平衡点，但其采用的牛顿法对初值的要求较高，很难保证初值在CUEP的收敛域内，故文章引入牛顿同伦法以降低CUEP求解对初值的敏感度。

2.1 主导负荷母线的确定

文献[5]采用暂态故障前后的电压幅值变化率作为评估电压薄弱节点的一种指标：

(2)

式中 电压差ΔV为故障消除时刻的电压值与故障发生前的电压值之差；V0为故障前的电压值。对该电压幅值变化率进行排序，选出变化率最大的负荷节点，其所在母线即为主导负荷母线。该方法较为充分考虑暂态故障前后的信息，而且对电压薄弱点的评估十分直观。此外，母线所带负荷的成分、参数不同，负荷母线与短路点的距离并非唯一决定最先发生暂态电压失稳母线的条件，因此，文章采用文献[5]所提出的电压薄弱节点确定方法来寻找主导负荷母线，而且可以看出，在能量函数法原有的计算框架下就已经获得求取主导负荷母线的信息，无需再进行额外的时域仿真。

2.2 主导不稳定平衡点初值的确定和修改

虽然一般情况负荷失稳不等同于电压失稳，但当系统发生短路故障时，节点电压降低导致感应电机负荷受扰而偏离稳态，而故障清除后，如果感应电机转子无法正常恢复转速，滑差增大甚至堵转将导致负荷失稳，此时感应电动机无功消耗与稳态相比更大，使得所接入节点电压更低，进而容易导致系统电压失稳。此场景下可出现负荷失稳和电压失稳相互交织，工程研究中计及电动机动态负荷模型时，常用电动机失稳条件(大滑差)对应电压失稳判定指标。文章基于一阶电动机模型，通过2.1的方法识别主导负荷母线，将主导负荷母线之外的系统根据故障后稳定平衡点(SEP)进行戴维南等值，再利用主导负荷母线相应电动机模型的转矩平衡方程，解一元二次方程，取较大的滑差值为式(3)中滑差变量的初值，其余变量以故障后SEP为初值，从而得到用于迭代CUEP的初值[14]。示意图如图1所示。

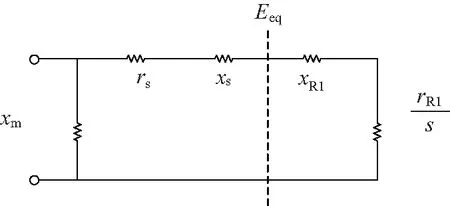
图1 一阶电动机等值示意图

在图1中，Eeq和req+jxeq分别表示对虚线左边系统进行戴维南变换之后的电势和阻抗，rR1+jxR1表示转子绕组的阻抗，s表示转子滑差。感应电动机稳态时转矩平衡条件为电磁转矩等于机械转矩，即：

(3)

式中 等号左边表示电磁转矩，等号右边表示机械转矩。为了方便文章的阐述，机械转矩采用滑差s来表示[20]，a、b、c是由于用滑差s来替代电动机转速ω而出现的，其中s=1-ω。

当按照上述的方法获得的迭代初值计算不收敛时，需要对迭代初值进行修改，目的是为了得到更加靠近CUEP的迭代初值。经验上，感应电动机滑差越大，越容易导致电压失稳。所以电压型CUEP的滑差值比SEP的更大。而且电压失稳往往从主导负荷母线向附近的母线扩散，所以电压型CUEP处的主导负荷母线及其附近的母线电压要比SEP的小。因此，将前述方法得到的主导负荷母线及其附近母线的电动机滑差值适当增大，以及将主导负荷母线及其周围母线的电压幅值适当减小，其余变量保持不变，这样获得的新的迭代初值更加靠近CUEP，以确保迭代更容易收敛到CUEP。

2.3 牛顿同伦法的实施

同伦法的基本思想为构造合适的同伦映射，通过预测-校正算法跟踪同伦方程的解轨迹以获得原非线性方程组的解[16,21]。设式(1)中的方程组为F(x)=0,x∈Rn。欲使用同伦法求解该方程组，首先引入参数t及辅助函数G(x)，构造同伦映射：

H(x,t)=tF(x)+(1-t)G(x)

(4)

式中H:Rn×R→Rn，G:Rn→Rn。而同伦路径即为满足当t从0到1变化时同伦方程H(x,t)=0的解。当t=0时，H(x,0)=G(x)=0的解x0为已知或者容易求解，当将t从0逐渐增加到1的时候，H(x,1)=F(x)=0的解为原来方程的解。

一般H(x,0)=0的解已知为x0，为求同伦方程的解曲线x=x(t)，对参数t求导可得：

(5)

求解微分方程组(5)主要分为以下两个环节：

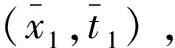
(6)

(7)

(8)

由于近似点已经比较靠近同伦方程(8)的解，故采用牛顿法对其进行求解，以近似点作为牛顿法的迭代初值，得到牛顿法的下一个修正量x1,1，则第k个修正量x1,k为：

(9)

为保证更可靠地找到电压相关的CUEP点，文章采用牛顿同伦映射[16]，如下式所示：

H(x,t)=F(x)-(1-t)F(x0)

(10)

在迭代初值相同时，牛顿同伦法比牛顿法更可靠地找到最靠近初值的原方程的解。牛顿法本质上是参数增量Δt=1的牛顿同伦法。由式(7)、式(10)可得牛顿同伦法的迭代增量为：

Δx=-(Fx(x0))-1F(x0)Δt

(11)

而牛顿法的迭代增量为：

Δx=-(Fx(x0))-1F(x0)

(12)

可见，当Δt=1时，牛顿同伦法与牛顿法是相同的。牛顿法对初值比较敏感，原因在于牛顿法的“参数增量”选得过大，很难保证每一次牛顿迭代后得到的迭代点更靠近原方程的解。而牛顿同伦法可以通过选取合适的参数增量，以确保每一次的预测-校正环节后都能得到更加靠近原方程的解的迭代点。

3 算例分析

文章采用主导不稳定平衡点法对含电动机系统进行暂态电压稳定分析，其计算原理如图2所示。

图2 暂态电压稳 定分析计算原理框图

3.1 含单个动态负荷母线的3机9母线系统

文章在PSAT[22]仿真平台上进行实验，所采用的仿真模型为3机9母线系统，系统参数可以参考文献[23]，该仿真模型结构图如图3所示。

图3 3机9母线系统

其中，发电机采用计及暂态电势动态的三阶模型；母线5和母线8连接恒阻抗负荷，母线6连一阶电动机负荷。电动机参数见表1，其余参数参考文献[24]。故障场景设为：于1.0 s时在母线7处发生三相短路，经一定时间后切除。

表1 电动机参数图

因为故障后不切除线路，所以故障后SEP即为故障前SEP。利用文章所述方法，计算得到较大的滑差值为0.050 7，将其作为初始值，其余变量以故障后SEP为初值，利用牛顿同伦法求解得到CUEP。为了形象展示CUEP是电压型UEP的特点，将SEP和CUEP投影到由G3发电机功角δ3、母线6电压幅值V6和滑差s构成的三维空间中，如图4所示。

图4 故障后SEP和CUEP投影图

对比图4中系统故障后的SEP和CUEP可以看出，两者的电压和电动机滑差值相差均较大，功角的差值较小，CUEP对应的电压值小和滑差值大，表明文章所用方法得到的CUEP是电压型UEP，也说明文章迭代初值的选取是合理的。

由于利用2.2节方法计算得到较大滑差值为0.050 7，为比较牛顿同伦法和牛顿法的收敛性能，将滑差初值在0.050 7附近变化，分别用两种方法对选取的滑差初值进行迭代，直到牛顿同伦法刚好不收敛到CUEP为止，计算结果见表2。当s0为0.045 7～0.359 0时，牛顿法收敛到CUEP；当s0为0.038 0～0.447 0时，牛顿同伦法收敛到CUEP。可以看出，欲收敛到CUEP，牛顿同伦法滑差迭代初值的范围和牛顿法对比，下界从0.045 7扩至0.038 0，上界从0.359 0扩至0.447 0。且牛顿法易发散或收敛到其它平衡点，而牛顿同伦法在收敛到CEUP前不会收敛到其它1型UEP。故初值相同时，牛顿同伦法比牛顿法更能可靠地找到CUEP，在计算上具有更高的鲁棒性。

表2 两种方法收敛结果

将CUEP和故障后SEP代入文献[25]的能量函数表达式，得系统临界能量值为2.087 3；对应的故障临界切除时间为1.224 s。而时域仿真法中，当故障切除时间为1.226 s和1.227 s时，电动机母线的电压曲线分别如图5、图6所示。

由图5和图6可以看到，当临界切除时间为1.226 s时，电压经一段时间恢复到故障前的值，当临界切除时间为1.227 s时，电压经过振荡后不能恢复到正常值，判定为暂态电压失稳，可知时域仿真法所得临界切除时间为1.226 s。直接法计算的临界切除时间与时域仿真的相比，两者误差仅为0.88%，满足工程精度要求。能量函数法所得临界切除时间比时域仿真法的小，体现的正是第二节所述的主导不稳定平衡点法固有的保守性。

图5 切除时间为1.226 s时电动机母线电压曲线

图6 切除时间为1.227 s时电动机母线电压曲线

3.2 含多个动态负荷母线的3机9母线系统

算例所用模型是在3.1系统的基础上，将其5号母线与8号母线的负荷都改成一阶动态模型表示的电动机，从而构成三台电动机的3机9母线系统。其中，8号母线所连电动机的滑差SEP值为0.009 07，其余参数同表1。为方便操作，取5号、6号母线所连电动机参数相同，见表3，其中5号、6号母线所连电动机滑差SEP值分别为0.009 33，0.009 28。根据推导的过程，电动机参数的选取不会影响文章方法的分析和计算。

表3 电动机参数

故障场景设为：在节点7处发生三相短路，经一定时间后清除。由2.1的方法可寻得主导负荷母线为8号母线。由2.2的方法计算得到较大的滑差值为0.047 3，将其作为初始值，其余变量以故障后SEP为初值，用牛顿同伦法迭代计算得到CUEP。求解得到的SEP与CUEP的局部投影见图7，其中s表示主导负荷母线电动机的滑差。

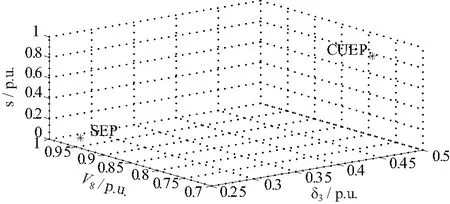
图7 故障后SEP和CUEP

对比图7中SEP和CUEP可以看出，两者的电压和电动机滑差值相差均较大，功角的差值较小，CUEP对应的电压值小和滑差值大，表明得到的CUEP是电压型UEP，说明此处迭代初值的选取是合理的。

运用前面的方法，求得系统临界能量值为2.275 3；对应的故障切除时间为1.125 s。同时，采用时域仿真法与之对比，当故障切除时间为1.131 s和1.132 s时， 8号电动机母线的电压曲线分别如图8、图9所示。显然，时域仿真法获得的准确系统维持暂态电压稳定临界切除时间为1.131 s，与文章所提的方法相比，两者误差为4.58%，满足工程精度要求。考虑到三电动机模型较单电动机模型更复杂，以及故障的地点的不同，这是三电动机算例在误差方面较单电动机算例大的主要原因。其中，三电动机模型中更多的动态负荷增强了系统的非线性，导致了系统在暂态过程中的电压波动更大，使系统更加容易发生电压崩溃。另外，当系统临近电压崩溃时，系统的雅克比矩阵接近奇异，仿真容易出现数值计算问题，这是图9电动机电压曲线在接近电压崩溃时剧烈振荡而后电压值出现为0的原因，但在实际中电压不为0。

为比较牛顿同伦法和牛顿法的收敛性能，按照3.1节算例的做法，令滑差初值在迭代算得的0.047 3附近变化，直到牛顿同伦法刚好不收敛到CUEP为止，两种方法的迭代结果见表4。显然，欲收敛到CUEP，牛顿同伦法滑差迭代初值的选取范围比牛顿法的更大，下界从0.045 0扩至0.037 2，上界从0.374 0扩至0.582 0。且牛顿法容易发散或收敛到其它平衡点，而牛顿同伦法在收敛到CUEP前不会收敛到其他1型UEP。可以看出，在初值相同的情况下，牛顿同伦法比牛顿法更能可靠找到CUEP，具有更高的鲁棒性。

图8 切除时间为1.131 s时电动机母线电压曲线

图9 切除时间为1.132 s时电动机母线电压曲线

表4 两种方法收敛结果

4 结束语

文中提出一种基于主导不稳定平衡点判断电力系统暂态电压稳定性的方法。为确保迭代初值更有效收敛到CUEP上，文章提出了启发式结合牛顿同伦法的思路，以计算电压相关的主导不稳定平衡点。另外，为使启发式方法更具普适性，文章还考虑多电动机的动态负荷模型，并通过识别电压薄弱节点寻得主导负荷母线。从仿真分析中可以看出：

(1)文章所提的方法用来求取临界切除时间与时域仿真的结果对比误差较小，具有良好的工程实用性；

(2)文章求得的CUEP在主导负荷母线上具有大滑差、低电压的特点，符合暂态电压失稳的特征，表明运用启发式结合牛顿同伦法的方法可以有效求取电压型CUEP；

(3)从表2和表4中可以看到，欲收敛到CUEP，牛顿同伦法滑差迭代初值的范围更大，表明牛顿同伦法较牛顿法更可靠地收敛到CUEP。

随着越来越多的电力电子型负荷接入电网，电力系统的暂态电压稳定机制也发生了深刻的变化，未来的研究将把文章的方法拓展到电力电子化系统中。