Daubechies小波系数新解法

张旭俊，张宇

(国网江西省电力有限公司电力科学研究院， 南昌 330096)

0 引 言

在大数据时代，小波是大量信号处理的有效时频分析工具[1-2]，在电气工程领域的谐波检测[3-4]、设备故障诊断[5]、故障选线[6]和继电保护[7]等方面有很高的实用价值。在经典小波中Daubechies小波(以下简称DB小波)是应用最广的，它充分体现了Daubechies思想的深邃和数学才华。但是经典的DB小波推演过程十分深奥，需要较多的数学知识，不便普及推广，文章的目的就是用普通的高等数学给出各种DB小波系数的计算方法，透彻的理解才能更好地灵活应用。为了深入认识，还把离散小波正交的概念引向正交的小波矩阵，即完全在时域中分析小波的分解与重构，可避免傅里叶积分变换的困扰。

1 双尺度分解

经典小波理论认为，尺度函数φ(t)和小波函数ψ(t)只在某一区间内有值，其余区间都是零，它和傅里叶级数分解不同，以分析128点采样数据为例，小波分解是用分段位移的逐次双尺度分解来分析函数的构成。对比傅里叶级数，小波是在选定的区间，用尺度函数对应滤出 0～32 Hz低次谐波部分，用小波函数滤出33 Hz ～64 Hz高次谐波部分。接着又对0～32 Hz低频谐波部分，进行双尺度分解为0～16 Hz更低的低频部分和 17 Hz～32 Hz的次高频部分。继续双尺度分解以达到对采样函数的多尺度分解。

尺度函数Φ(t)或小波函数ψ(t)可以由高一倍频率的尺度函数Φ(2t)及其位移Φ(2t-n)的线性组合构成，即：

(1)

(2)

它们的傅里叶变化函数Φ(ω)和Ψ(ω)可推出如下：

(3)

同理有：

(4)

且有如下关系：

(5)

从物理意义上说，尺度函数Φ(ω/2)的频率比Φ(ω)频率高一倍，而H(ω/2)相当于滤波函数。

令z=e-jω，滤波函数H(ω)可表达如下：

(6)

(7)

尺度函数和另一平移后的尺度函数应当是正交的，用如下公式表示：

ejωmdω=δ0,m

(8)

为了达到正交的目的，只当m=0时，才会有δ0,0=1，这需要满足式(9)的恒等式关系。其中应用了双尺度关系式(3)。

(9)

根据H(ω)=H(ω+2mπ)的周期性，在式(10)推导中，并将其中整数k依奇、偶数分割成2m和2m+1两部分，推导得出：

(10)

依尺度正交的恒等式(9)，也应有如下关系：

(11)

将式(11)代入式(10)可得：

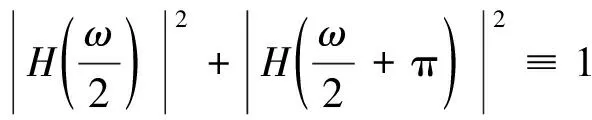
(12)

或写成如下形式：

|H(ω)|2+|H(ω+π)|2≡1

(13)

2 Daubechies滤波函数H(ω)系数的计算

依据三角函数立即可看出如下的一组解，设H1(ω)=cos(ω/2)，则H1(ω+π)=cos[(ω+π)/2]=-sin(ω/2)，它符合式(13)，这就是Haar小波。依式(6)可得：

(14)

(15)

Daubechies思路的巧妙在于，依据三角函数的二项式高次幂展开，而得出的更多层次的DB小波。为了进一步说明Daubechies各种层次下的DB小波系数的计算方法，可依据恒等式(16)展开，并将它分成两部分：

(16)

为了书写简化，令C=cos(ω/2)；S=sin(ω/2)，取二项式展开的前半部分为|H(ω)|2，如公式(17)所示，二项式的后半部分为|H(ω+π)|2，如公式(18)所示：

(17)

(18)

式(17)中直接将S⇒C和C⇒S即可得式(18)。上面的系数就是二项式展开的杨辉系数，计算简单。关键是要求出滤波函数H(ω)的系数。

(19)

下面举例如下： 令N=5，依式(17)可得：

(20)

令：

A(ω)=C8+9C6S2+36C4S4+84C2S6+126S8

(21)

令：

(22)

可得高次多项式，通过解高次方程，将其分解成多个二项式的乘积，即：

(23)

将T还原到三角函数：

A(ω)=|B(ω)|2=|D1(ω)·D2(ω)|2=

(24)

为了求出|B(ω)|，可将每个二次多项式配方，转成|Dk(ω)|2=|u2+v2|模式，求出共轭复数，在式(25)中任取一个复数就是它的解。

Dk(ω)=uk±jvk

(25)

(26)

对其中每一个因子分式代入C2=(1+cosω)/2；

S2=(1-cosω)/2；CS=sinω/2。并令z=ejω，并|z|=1可得：

(27)

其中：

(28)

注意C5=z-5/2[(1+z)/2]5，于是一般形式可得：

|H(ω)|=|C5·B(ω)|=

(29)

可取：

(30)

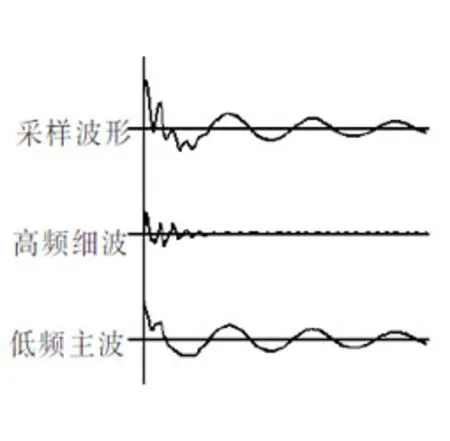
当式(28)中取正符号时有M2k>M0k，而取负符号时有M2k

表1 实例计算比较Daubechies的DB小波和SYM对称小波尺度波形系数

Daubechies小波DB10和SYM10小波波形的对比图见图1。可见，SYM10的小波相比于DB10小波波形更具有对称性。

图1 Daubechies小波DB10和SYM10小波波形的对比

3 多尺度DB小波系数的计算

依据式(3)连续变换Φ(ω/2k)乘积可得：

(31)

采用连乘积的办法得到式(31)，似乎不能求解出Φ(2ω)，其实从递推公式的角度看Daubechies尺度函数的解已经求出。首先注意对于等时间隔采样的函数而言，最高次频率是有限的，ω≤ωmax所以当N→∞时有ξ=ω/2N⟹0。因而有Φ(ω/2N)=Φ(ξ)≅Φ(0)，而Φ(0)≠0，否则会有Φ(2ω)≡0，这不合理。可取Φ(ξ)=Φ(0)=1，于是有递推关系式：

(32)

由于傅里叶反变换，有：

zn=ejnξ⟹δ(t-n)

(33)

求出尺度波形是一串离散的数据，即：

(34)

(35)

(36)

对于多尺度小波的计算，可从递推公式着手，并注意傅里叶变换的对等关系：

(37)

(38)

其中uk(k=0,1,2,...,M-1)共有M项，一般说对于DB2N小波在第k尺度下，尺度波形的点数M可通过式(39)计算，且uk满足式(40)的关系。

M=(2N-1)·(2k-1)

(39)

(40)

第3尺度的尺度波形共有M个点，即：

(41)

图2、图3中分别示出DB10小波和SYM10近似对称小波在3种尺度波形和小波波形的对照图。可见，不论是DB10小波还是SYM10小波，其尺度1～3下的小波波形和尺度波形的特征相似，时间跨度依次以2倍递增。

图2 DB10小波在3种尺度下的尺度波形Φ(t)和小波函数ψ(t)

图3 SYM10小波在3种尺度下的尺度波形Φ(t)和小波函数ψ(t)

4 小波矩阵与小波的分解与重构

为了清楚地表达小波的正交性和小波分析的分解和重构，特引出小波矩阵[9-10]，现以DB4小波为例，其尺度波形的数据如下[11]：

(42)

对应的也有小波波形4个数据gk=(1)kh3k，限于矩阵篇幅，设定采样数据只有8个点(一般可扩展到2N个数据)，小波矩阵B[8×8]，见式(43)，从第0行开始排列尺度波形系数，而第1行参数相对第0行位移2个列，其余都是0。到第3行有h2、h3超出矩阵B[8×8]范围，需要循环移位到第0列、第1列中。同理从第4行开始排列小波波形系数。B矩阵中上面4行构成尺度波形矩阵H[4,8]，下面4行构成小波波形矩阵。B矩阵的优点是它具有正交性，即它和自身的转置矩阵互为逆矩阵，即BTB=E，其中E是单位矩阵,符合公式(44)。

(43)

(44)

B矩阵可以按2次幂扩展，如对128点采样数据F[128]作小波的分解与重构，B矩阵就是128阶的方阵B[128×128]，小波分解计算如下：

(45)

其中C[64]是反映采样波形沿分段的时间轴与尺度波形的相关系数。而D[64]是反映采样波形沿分段的时间轴与小波波形的相关系数，数据减少一半，称为二倍压缩。双尺度分解可以通过小波重构得到低频的主波F1[128]和高频的细波X1[128]，称为二倍膨胀。计算公式如下：

F1[128]=HT[128,64]·C[64]

(46)

X1[128]=GT[128,64]·D[64]

(47)

依据小波矩阵正交的式(43)可知，低频主波F1[128]和高频细波X1[128]的合成还原了原采样波形F[128]，如下：

F[128]=F1[128]+X1[128]=HTH·F+GTG·F=F

(48)

5 更多的正交小波引入

依照文中推证的方法，可以很方便地引出一系列另类的正交小波，如把原来式(20)的|H(ω)|2经过式(49)改写成|Hm(ω)|2：

(49)

当其中参变数m若满足126>m>0的关系时，则|Hm(ω)|2也满足如下的恒等式关系：

|Hm(ω)|2+|Hm(ω+π)|2≡1

(50)

6 工程应用案例

小波分析应用的范围很广，涉及各个领域。如图4所示,对三种128点采样波形，经过采用DB10小波的双尺度分解后，得出的“低频主波”和“高频细波”[12]，依据波形频次不同，三种波形分解和重构所采用尺度等级各不相同，三种波形的特征如图4所示。

图4 典型电气工程波形的小波分解Fig.4 Wavelet decomposition of typical electrical engineering waveform

故障时刻：小波分析主要指出故障发生时刻，和暂态电流的高次衰减波形，后者有时可用于接地选线的判断分析。其尺度时谱和低频主波的趋势是一致的。

励磁涌流：即变压器空载合闸电流，可通过低频主波的分析，可用二次谐波制动来避免合闸励磁涌流的误动，也可分析剩余磁通衰减过程。

瓷瓶(绝缘子)放电：这是多个电容串联分压的模型，放电瓷绝缘子相当于放电电容并联一放电间隙。当正常充电达到该瓷绝缘子间隙的放电电压时，瓷绝缘子放电，相应电容电压降为零，绝缘恢复。接着充电又开始，反复放电，其平均电压很低，它的低频主波也不是正弦波。

目前柔性输电、谐波和无功治理等专业领域都涉及开关函数波形，图5所示例子为采用双正交小波对开关函数波形进行3级尺度的小波分解，得出低频主波为变化的三角波。

图5 用双正交小波分解开关函数波形

在小波分解和重构中还存在边缘失真的问题，如图6中128点的采样波形，开始点的数值比末尾点幅值高很多，即首尾数值存在变化剧烈的差值。由于正交小波矩阵是循环移位构成的，会发生首尾边缘失真问题，如图6中E、F两点所示。

图6 波形首尾数值变化剧烈而产生的边缘失真Fig.6 Edge distortion caused by drastic changes in the

解决边缘失真问题的方法，可使用镜像法，将原始128点数据扩展成256点，此时首尾点的数值相等，再进行256点扩展数据的小波分析。如此就能完全消除边缘失真效应，如图7所示。为了和图6比较，其中只显示前128点的小波分析结果。

图7 通过镜像扩展一倍点数后进行小波分析的结果Fig.7 Result of wavelet analysis after doubling the number of points by mirroring

7 结束语

文章完整地把经典小波理论用一般的高等数学加以演绎推导，通俗易懂。按照文中的思路，提出了更多新的正交小波尺度波形构造方法。工程应用中，对于波形首尾数值变化剧烈而产生的边缘失真问题，采用镜像扩展一倍点数后进行小波分析可有效消除失真效应。