钢支撑- 框排架结构动力试验及有限元分析
2022-12-17高向宇李振宇史安琪王作杰刘凯雁李杨龙张国伟
高向宇, 李振宇, 史安琪, 王作杰, 刘凯雁, 李杨龙, 张国伟
(1.北京工业大学城市建设学部, 北京 100124; 2.北京构力科技有限公司, 北京 100013;3.中国电力工程顾问集团华北电力设计院有限公司, 北京 100120;4.北京建筑大学土木与交通工程学院, 北京 100044)
大型电力主厂房是一类很特殊的工业厂房,其作为重要生命线工程,承担着电力能源供应的重要任务,一旦在地震中受损或发生破坏导致电力供应中断,将难以发挥应有的生命线功能[1]. 随着国家电力行业的发展,单机容量不断增大,结构高度、跨度、荷载也不断增加,使得结构动力特性更为复杂,结构所承受的地震作用也更大,在高烈度地区采用传统的钢筋混凝土框排架电力主厂房结构已不适合. 《火力发电厂土建结构技术设计规程》[2]中提到,设防烈度8度Ⅱ~Ⅳ类场地主厂房宜采用钢结构框架- 支撑体系. 然而,由于生产工艺及功能的要求,电力主厂房需要将不同跨度、高度的框架和框架- 支撑结构并列布置,并且存在错层、去板等不利的结构构造,使得结构刚度分布不均匀. 另外,煤斗层质量较大,占结构总质量的20%~30%,造成了结构质量分布不均,在地震作用下,结构受力复杂,薄弱位置较多[3]. 对于火电厂主厂房抗震设计所具有的特殊性,我国现有的钢结构设计规范和抗震设计规范尚缺乏相关的针对性规定条款.
已有很多学者对钢支撑- 框排架结构体系展开研究,张文元等[4]对大型火电厂铰接中心支撑- 框排架结构进行振动台试验和有限元分析,结果表明该类结构顶部及底部层间位移角较大且顶部存在一定鞭梢效应. 薛建阳等[5-6]对单榀钢框排架结构进行了拟动力试验,并采用SAP2000软件对试验结果进行了建模验证,分析表明,钢框排架结构延性相对较好,具有良好的抗震性能. 江菊[7]通过SAP2000对采用钢支撑及偏心支撑的火电厂结构进行推覆分析,结果表明支撑位置的改变对结构整体刚度影响较大,采用偏心支撑能显著提高结构的抗震能力且在错层、刚度突变以及未布设支撑部位结构反应增大. 梁炯丰[8]对单榀钢支撑- 框排架结构进行了拟静力及拟动力分析,试验结果表明煤斗梁刚度过大,使得相邻节点容易成为结构的薄弱部位. 徐吉民等[9]对单榀钢支撑- 框排架结构进行低周往复加载,试验结果表明结构底部支撑为最初破坏部位,塑性铰发展顺序为先梁端后柱端,最终柱呈压弯形破坏. 高向宇等[3]通过SAP2000有限元软件研究了钢支撑- 框排架结构火电厂非弹性扭转机理,分析表明钢支撑屈曲失稳导致框排架结构出现非弹性扭转并导致地震响应突增. 戴靠山等[10]采用Perform3D有限元软件基于纤维截面对钢支撑- 框排架结构进行弹塑性时程分析,并与SAP2000计算结果进行了对比,结果表明钢支撑屈曲后结构出现明显薄弱层. 王富民等[11]对单榀缩尺钢支撑- 框排架结构进行拟静力低周往复加载试验,试验结果表明,钢支撑屈曲后会使与其相连的节点、钢梁等发生扭曲,加剧结构平面外弯曲,对整体结构抗震不利.
已有文献大多针对主厂房单榀或局部结构进行试验研究,关于钢支撑- 框排架整体结构的试验研究较少,因此,本文对常规钢支撑- 框排架电力主厂房结构进行缩尺比例为1∶20的振动台试验,研究电力主厂房结构在设防烈度为8度(0.2g)场地条件下频率变化、层间位移角分布、地震动峰值加速度放大系数响应以及结构损伤分布,并建立相应缩尺有限元模型,与试验结果进行对比验证,随后对结构薄弱部位进行加固分析,并提出相应设计建议.
1 试验设计及有限元建模
试验原型为某1 000 MW超超临界燃煤机组主厂房[12],结构抗震设防烈度为8度,设计基本地震加速度为0.2g,设计地震分组为第1组,场地类别为Ⅳ类,场地特征周期为0.65 s,各荷载的重力代表值组合系数按《火力发电厂土建结构设计技术规程》[2]取值. 试验在北京建筑大学大型多功能振动台台阵实验室进行,所选用振动台台面尺寸为 5 m×5 m,最大承受质量为60 t,最大加速度为1.5g,确定长度相似比为1∶20,质量相似比为1∶1 280,试验模型采用钢材制作,弹性模量相似比为1∶1,由以上3个物理量按相似理论即可推导出其余物理量的相似关系,其中时间相似比为1∶8,加速度相似比为3.2∶1, 应力、应变相似比为1∶1. 试验模型质量约31 t,如图1(a)所示,坐标轴、轴网布置及楼层分布如图1(b)(c)(d)所示. 考虑到煤斗所产生的荷载直接传递给煤斗梁,因此,将煤斗等效为砝码,并添加钢制楼板与螺栓将其锚固在煤斗梁,具体砝码锚固方案如图1(a)所示. 由于部分构件截面按照 1∶20缩尺后难以加工,将部分梁、柱截面按等承载力原则替换为方管、圆管,其中D轴、1轴立面的梁、柱尺寸及位置分布如图1(c) (d)所示,钢支撑截面尺寸及位置如表1所示. 图中,“□40×20×1”表示截面为矩形方管,长、宽、壁厚分别为40、20、1 mm. 模型纵向由9榀框排架组成,总长为3 900 mm;横向总跨度为2 850 mm,主要分为3跨:汽机房(AB跨)、除氧间(BC跨)、煤仓间(CD跨),三部分跨度分别为1 700、500、650 mm;模型总高为2 638 mm,试验模型详细信息见文献[13-15].

图1 振动台试验及有限元模型(单位:mm)Fig.1 Shaking table test and finite element model (unit: mm)
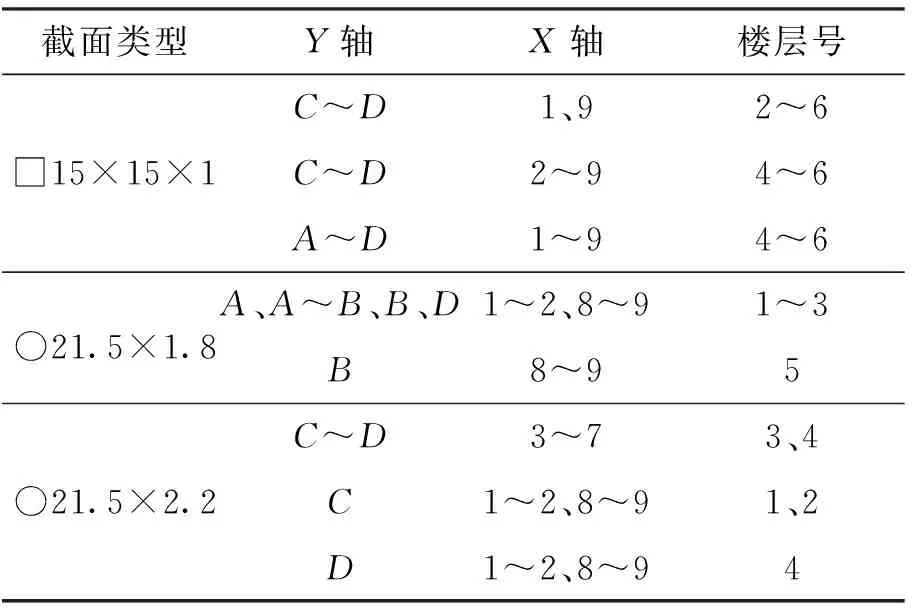
表1 钢支撑截面尺寸及位置
采用ABAQUS有限元软件建立了相应缩尺有限元模型,如图1(b)所示. 结构梁、柱及钢支撑均采用B31梁单元,钢材型号为Q235,材性试验结果如表2所示,采用考虑钢材随动强化特征的双线性本构模型,梁、柱及支撑截面形式与试验模型一致,楼板采用壳单元,试验模型中所添加的附加质量块以分布质量(面质量)的方式按实际分布情况施加在楼板单元上. 楼板边缘与梁、梁柱节点采用Tie约束,模拟焊接效果.
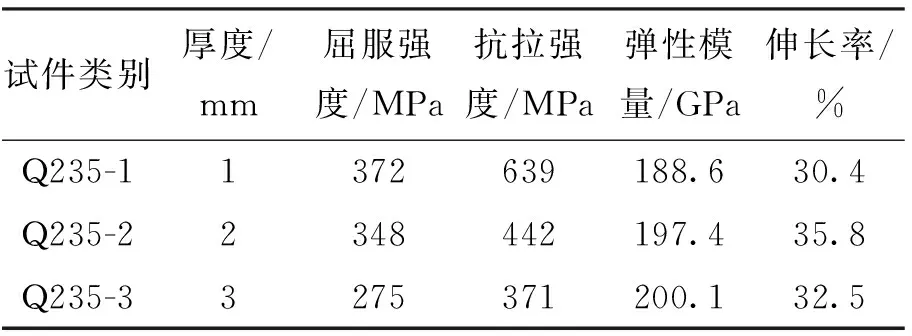
表2 钢板材性
2 地震波选波及试验工况
依据结构原型场地条件在PEER[16]上选取4条天然波以及1条按照规范谱生成的人工波. 为了便于表述,这里选用有代表性的2条天然波以及1条人工波进行讨论,3条地震波信息如表3所示. 3条地震波反应谱加速度as及地震波加速度aw时程曲线分别如图2、3所示. 下文将3条地震波分别记作“NR2波”“CV波”“RGB波”.

表3 地震波信息
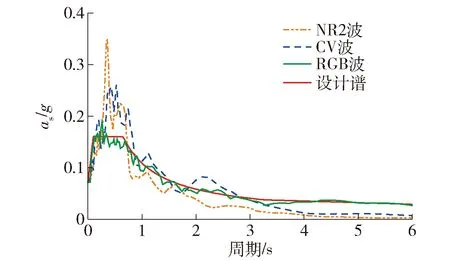
图2 地震波反应谱Fig.2 Response spectra of the ground motions
在试验工况上,按照加速度相似关系分为3级加载,输入的地震动峰值加速度为0.224、0.672、1.280g,分别对应《建筑抗震设计规范》[17]中8度(0.2g)多遇地震、设防烈度地震、罕遇地震. 每级地震水准为1个试验组,每个试验组中按照时间相似比以及加速度相似比将地震波调幅后分别沿结构X向、Y向依次输入NR2波、CV波、RGB波. 在试验开始前和每个试验组之间以及试验结束后分别进行白噪声扫频工况,以检测结构动力特性的变化. 试验工况如表4所示.
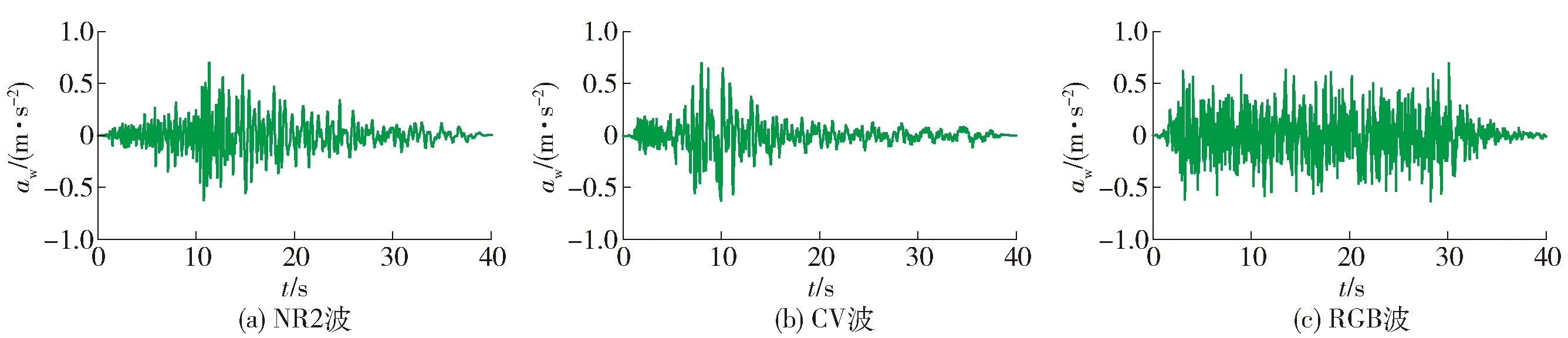
图3 地震波加速度时程曲线Fig.3 Acceleration time history curve of seismic wave
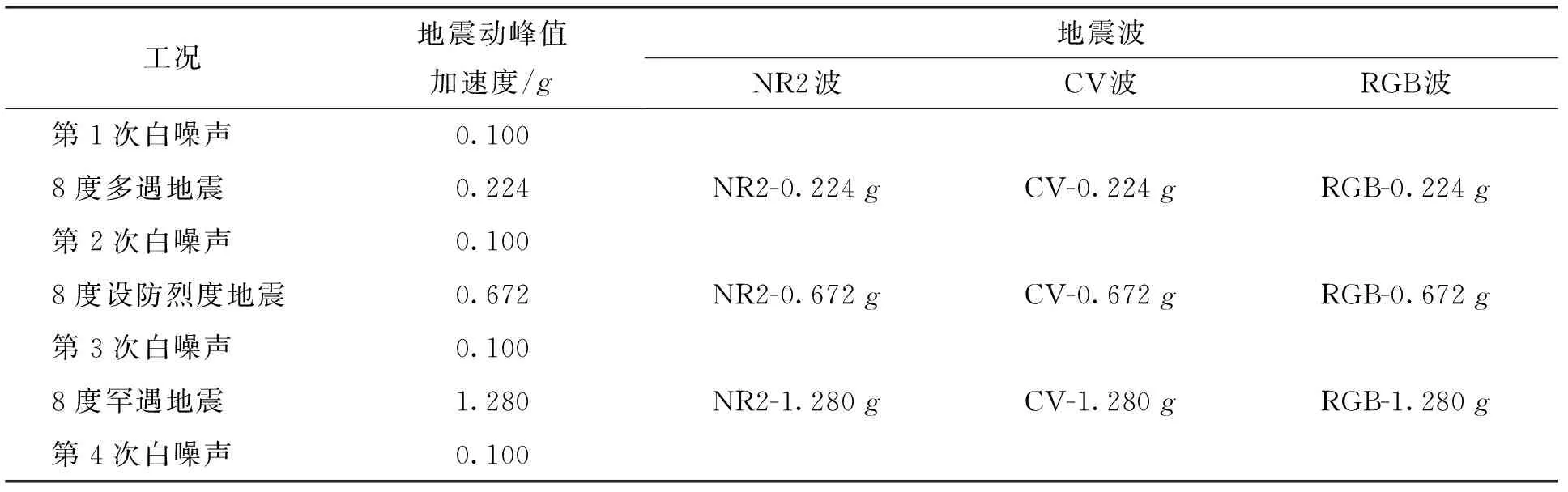
表4 试验工况
3 试验结果
3.1 试验现象
试验模型在多遇地震作用下,未观测到明显变形及损伤;在8度设防烈度地震下,主体结构未发现明显变形,A轴排架第4层钢支撑端部开焊,如图4(a)所示. 8度罕遇地震下,试验模型响应更加激烈,试验结束后发现煤仓间(D轴)第5层X向两端柱间支撑发生屈曲及断裂,B轴、C轴第5层X向支撑端部开焊,如图4(b)(c)所示. 总体上来看,结构破坏主要发生在第5层沿X向布置的钢支撑,结构Y向未发现支撑及梁柱构件损伤.

图4 结构损伤分布Fig.4 Distribution of structure damage
3.2 动力特性验证
各级白噪声工况扫频结果如图5所示. 可以看出,8度多遇地震作用前后结构前3阶频率降幅较小,说明模型处于弹性状态. 8度罕遇地震后,结构前3阶频率均有不同程度的降低,第3阶频率降幅较为明显,从9.287 Hz降低至8.541 Hz,降低了约8.0%,这些变化是因为罕遇地震下部分钢支撑屈曲对结构扭转控制能力减弱. 试验结束后,前3阶频率分别降至试验前的90.4%、 91.6%和 87.1%.
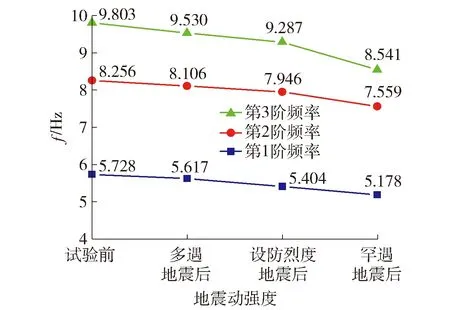
图5 频率变化Fig.5 Change of frequency
3.3 层间位移角响应
图6为8度罕遇地震在3条地震波分别沿结构X、Y向作用下结构层间位移角分布情况. 图中,实线实心标记表示振动台试验结果,虚线空心标记表示ABAQUS有限元模型计算结果. 在罕遇地震作用下,3组波X、Y向层间位移角最大值分别为 0.008 4、0.005 5(试验值),满足《建筑抗震设计规范》[14]的抗震设防要求(罕遇地震下多、高层钢结构弹塑性层间位移角限值为1/50). 结构X向层间位移角大于Y向,两水平方向顶部层间位移角均较大,结构顶部为薄弱环节. 其中:X向层间位移角最大值发生在第5层位置,1~5层层间位移角逐渐增大,在第6层略有减小;结构Y向1~4层层间位移角较为均匀,4~6层略有增加.
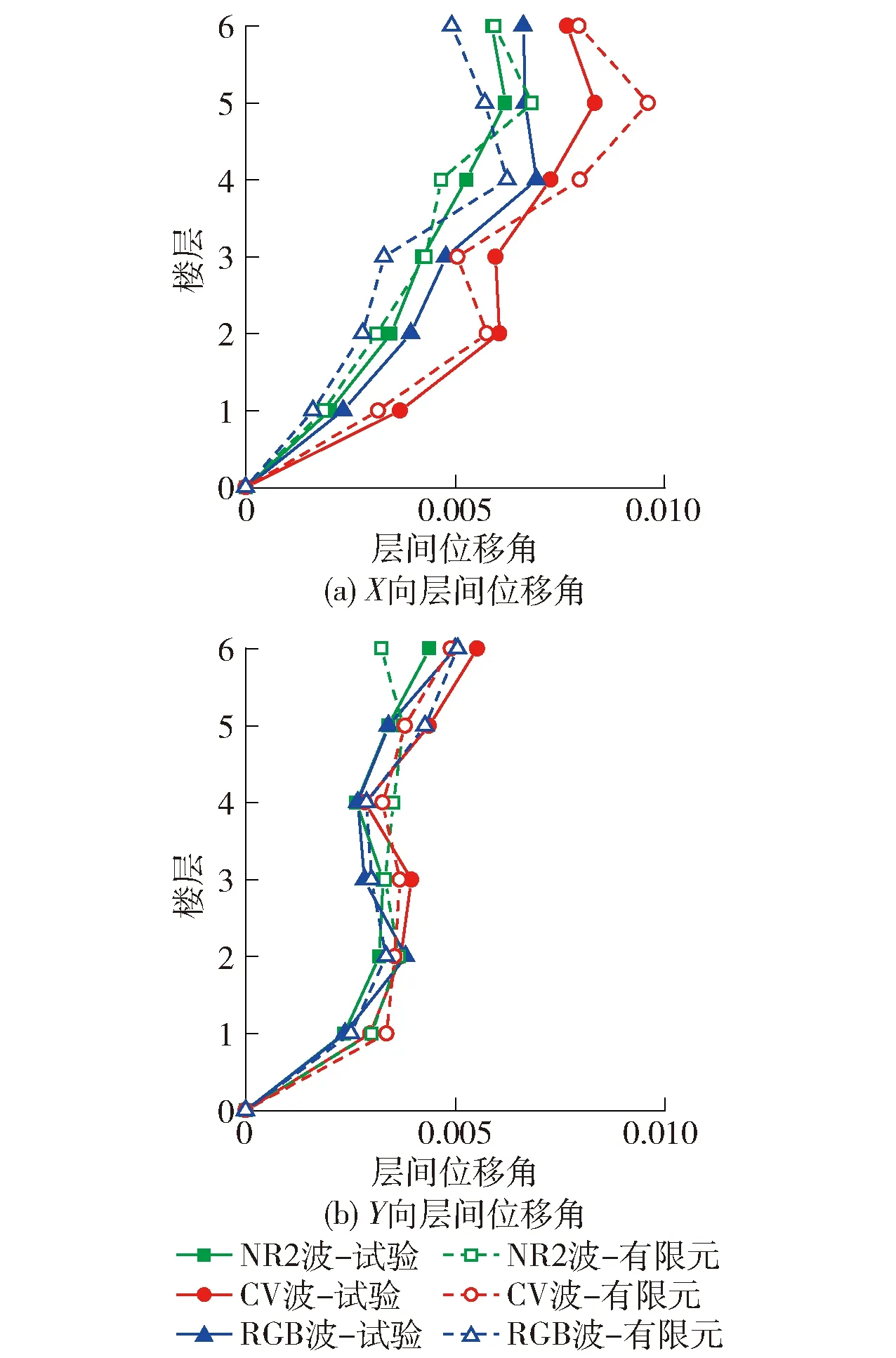
图6 8度罕遇地震层间位移角Fig.6 Inter-story drift ratio in 8-degree rare earthquake
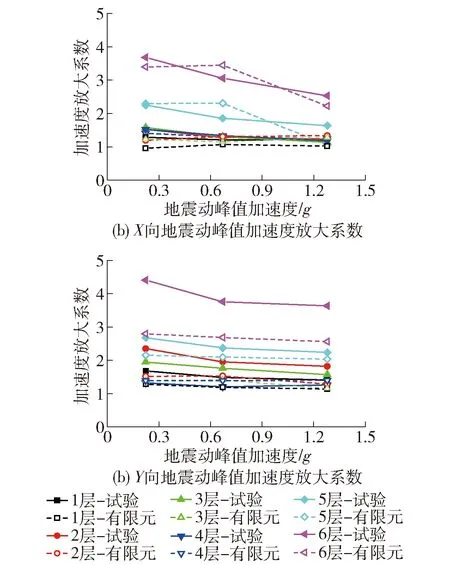
图7 在CV波作用下各楼层加速度放大系数Fig.7 Acceleration amplification factor for different floors under CV wave
3.4 地震动峰值加速度放大系数
在CV波作用下,结构响应最大,因此,图7(a) (b)分别列举了8度多遇地震(地震动峰值加速度为0.224g)、8度设防烈度地震(地震动峰值加速度为0.672g)、8度罕遇地震(地震动峰值加速度为1.280g)试验模型在CV波分别沿结构X、Y向作用下各楼层地震动峰值加速度放大系数(各楼层测点峰值加速度与台面输入地震动峰值加速度的比值). 图中,实线实心标记表示试验结果,虚线空心标记表示有限元计算结果,并通过颜色及标记形状区分楼层响应. 从图中可以看出,在X向地震作用下,同一烈度地震动峰值加速度放大系数在底层变化缓慢,在第4、5层沿高度略有增大,第5、6层又有明显增大,尤其是第6层. 这些现象表明:试验模型振动是倾向于以第1阶模态为主;结构顶部存在一定鞭梢效应. 从图中还可以看出,随着输入地震波幅值的增加,试验与有限元结果均表现出同一楼层地震动峰值加速度放大系数呈逐渐降低的趋势,尤其是结构顶部第5、6层. 在8度罕遇地震时,地震动峰值加速度放大系数试验值分别降低了27.4%、31.4%. 这说明随着地震烈度的增大,结构内部构件或节点逐渐进入塑性,滞回耗能降低了各层的地震动峰值加速度放大反应.
试验模型Y向地震动峰值加速度放大系数略大于X向且随着输入地震动峰值加速度的增加,各楼层地震动峰值加速度放大系数降低较缓,第6层降幅略微明显. 在8度罕遇地震后,地震动峰值加速度放大系数试验值降低了17.5%,说明结构在Y向地震作用下整体损伤较小. 另外,有限元第6层地震动峰值加速度放大系数与试验误差较大,分析原因为结构第6层沿结构Y向为弱轴,模型顶部附加质量块(见图1(a))加重了鞭梢效应.
3.5 楼层扭转响应
将同一楼层对角测点位移相减后除以两测点间距,即可得到各楼层扭转角时程曲线;将相邻楼层扭转角作差,即得到层间扭转角时程. 图8为NR2波、CV波、RGB波在多遇地震、设防烈度地震及罕遇地震下的层间扭转角,沿楼层增加,层间扭转响应逐渐增大,在结构的第4层扭转角突然减小,这是因为该层包含屋盖,楼板较为完整,抗扭刚度显著提升,并且随着地震烈度的增大,这种突变现象愈发明显.
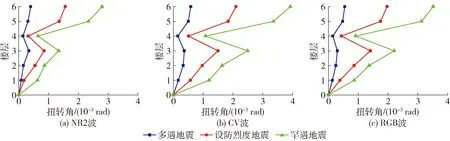
图8 层间扭转角Fig.8 Interlayer torsional angle
以结构在多遇地震下的响应为基准,各烈度下结构扭转角峰值以及X、Y向各楼层地震动峰值加速度放大系数最大值与多遇地震作用下响应的比值如图9所示. 可以看出,随着地震动峰值加速度的增加,2个水平向的加速度放大系数相比多遇地震略微下降,而扭转角放大系数相比多遇地震逐渐增加. 试验中多遇地震、设防烈度地震、罕遇地震输入地震动峰值加速度分别为0.224、 0.672、1.280g.

图9 层间扭转角及地震动峰值加速度放大系数Fig.9 Interlayer torsional angle and peak ground acceleration amplification factor
4 有限元计算结果
有限元模型所计算的层间位移角及地震动峰值加速度放大系数响应分别如图6、7所示. 从图中可以看出,有限元计算结果与试验结果相近. 为找出钢支撑- 框排架结构薄弱部位,并探究试验模型破坏部位是否因焊接质量所造成,利用ABAQUS软件强大的非线性运算能力,分析了结构振型、顶点位移曲线、结构损伤情况及相应的加固措施,对试验研究进行补充.
4.1 振型及频率对比
图10为ABAQUS模型的前3阶振型,表5为有限元与试验模型前3阶频率对比,二者接近,第1~3阶误差分别为9.62%、3.25%、0.19%. 振型的顺序为沿X向平动、沿Y向平动、扭转,顺序合理. 从第3阶振型图中可以看出,电力主厂房结构存在较大偏心且偏心主要分布在结构Y向. 另外,计算结果与试验结果相比,第2、3阶频率误差较小,第1阶频率存在一定误差. 分析原因是试验采用的是钢制质量块,有限元模型采用的是面质量模型,二者存在差异.
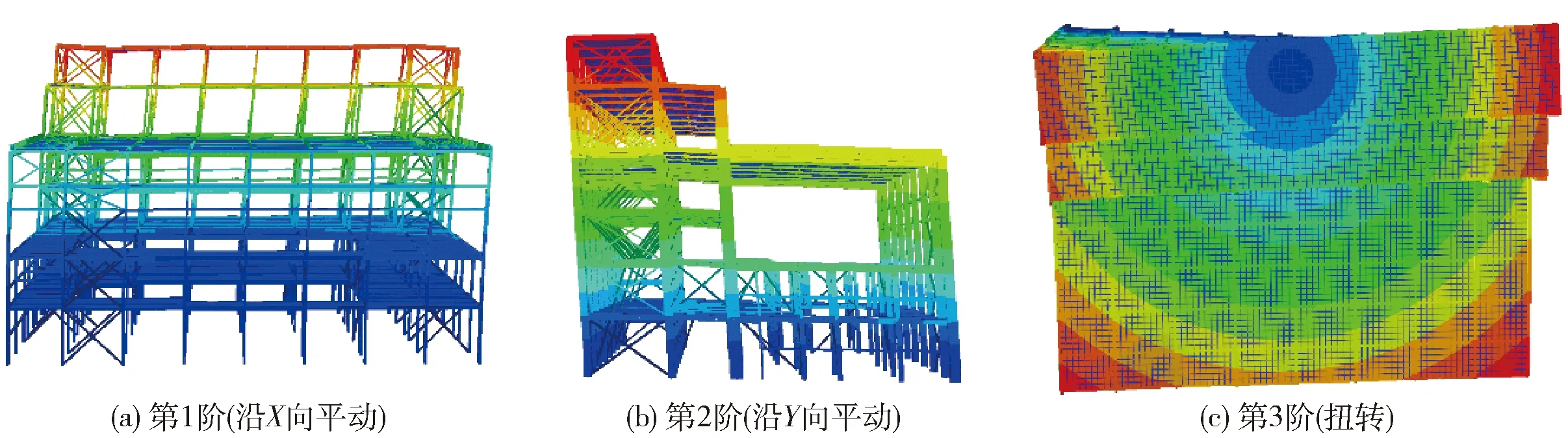
图10 有限元模型前3阶振型Fig.10 First three vibration modes of finite element model
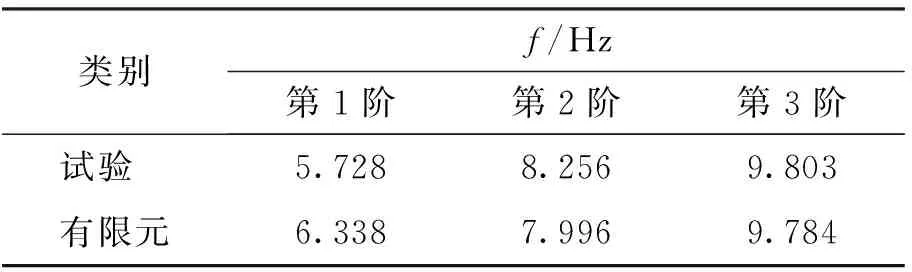
表5 有限元与试验模型的频率
4.2 顶点位移时程曲线对比
在8度罕遇地震作用下有限元与试验顶点位移时程对比情况如图11所示,X、Y向顶点测点分别如图1(b)所示. 图中“CV-X-1.280g”表示CV波地震动峰值加速度为1.280g,沿X向输入结构. 由图可见,有限元结果与试验结果相近且振动趋势相似.
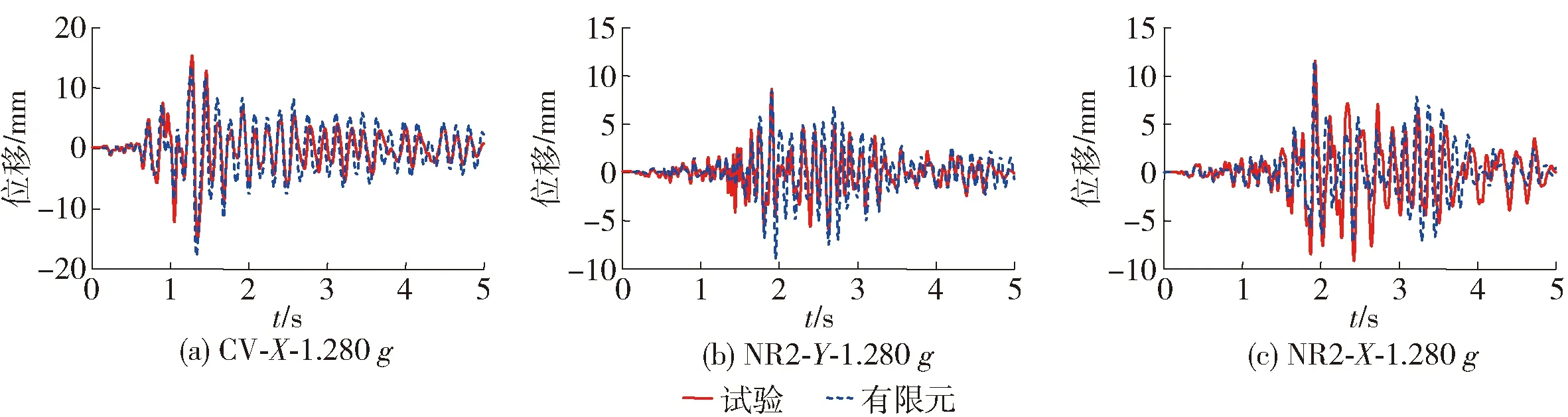
图11 顶点位移时程曲线Fig.11 Displacement time-history curves of the top point
4.3 损伤分布对比
图12为8度罕遇地震CV波沿X向输入有限元模型的结构累计塑性损伤分布情况. 图中数字表示各构件进入塑性的顺序,标红部位表示该部位进入塑性. 可以看出,首先B、C、D轴第5层1~2轴(轴网布置见图1(c)(d))沿X向布置的钢支撑发生屈曲变形,随后A轴第4层1~2轴的钢支撑也进入塑性,接着D轴第5层8~9轴的支撑屈曲失稳. 整体上,有限元模型的损伤分布基本与试验观测到的一致,见图4. 在破坏形式上,由于试验模型中钢支撑壁厚约1.0~2.5 mm,焊接时可能存在一定的加工质量误差,导致试验过程中部分支撑端部开焊,所建立的有限元模型未考虑构件开焊的影响,但模拟结果损伤部位仍与实验结果一致,表明焊接质量的影响较小,结构薄弱部位为第5层沿纵向布置的钢支撑.
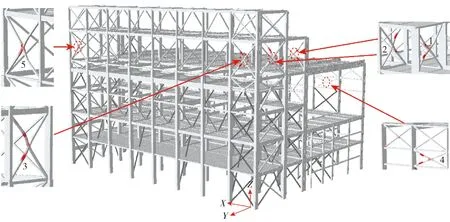
图12 8度罕遇地震CV波X向作用下结构损伤分布Fig.12 Structure damage distribution under X-direction of CV wave in 8-degree rare earthquake
4.4 加强第5层X向钢支撑
由试验及有限元模拟结果可知,钢支撑- 框排架结构损伤主要为第5层X向钢支撑发生屈曲及破坏,因此,将该层X向钢支撑替换为等壁厚且截面面积增加至原截面1.5倍的方管或圆管. 表6为第5层X向钢支撑加强前后的尺寸信息. 图13为加强后8度罕遇烈度下CV波沿X向作用的结构损伤情况. 通过对比图12、13可以看出,加强第5层X向支撑后,该层支撑未发生屈曲变形,由于未加固A轴第4层位置钢支撑,该位置的支撑仍出现损伤(损伤部位在右下局部图中红色标出),表明所采用的加强措施有效.

表6 加强前后第5层X向钢支撑截面信息
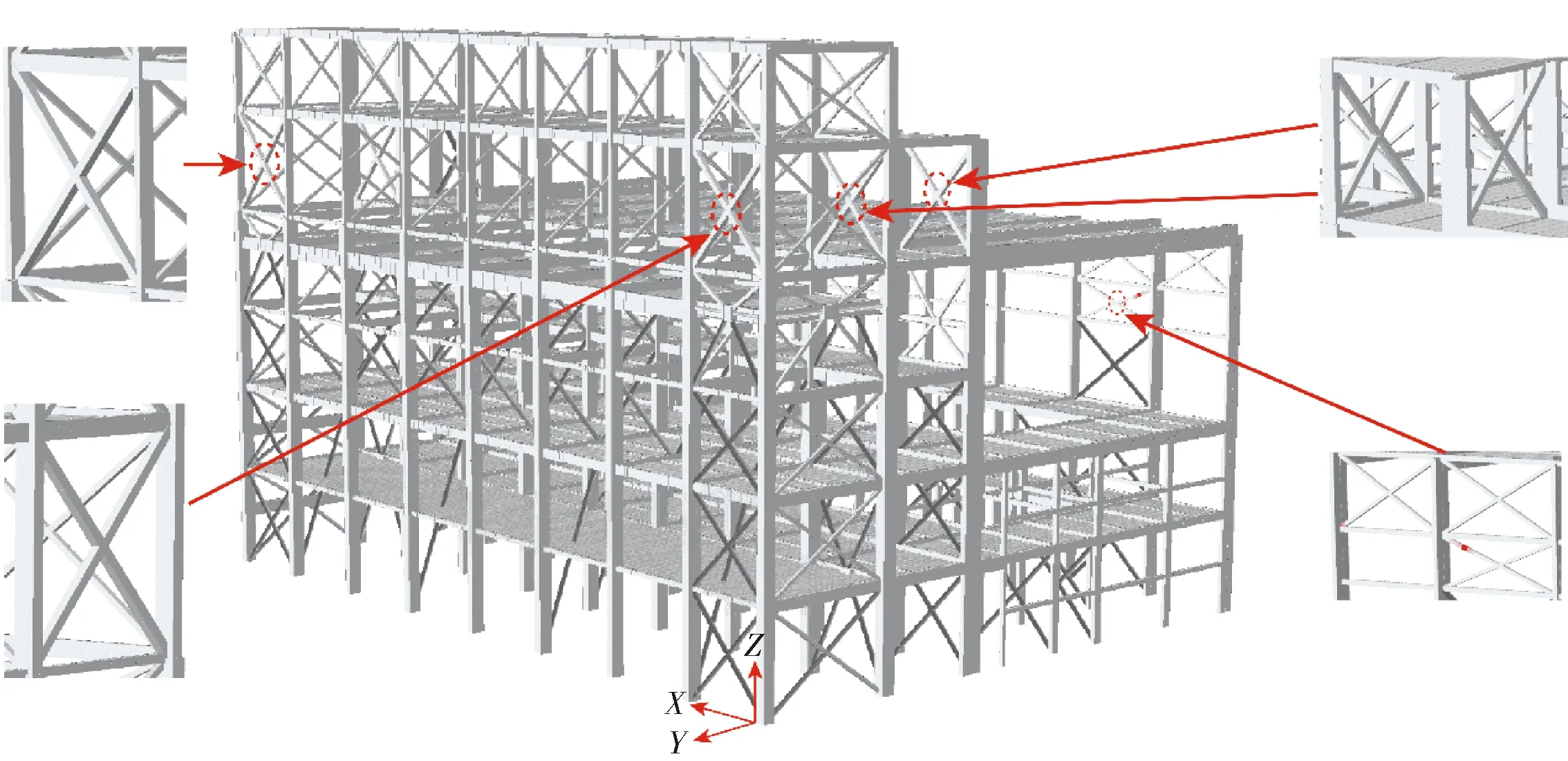
图13 加强后8度罕遇地震CV波X向作用下结构损伤分布Fig.13 Structural damage distribution under X-direction of CV wave of 8-degree rare earthquake after reinforcement
5 结论
1) 通过振动台试验以及与有限元计算进行对比,研究了钢支撑- 框排架结构在8度地震作用下加速度、位移、动力特性及损伤情况. 试验发现,钢支撑出现不同程度的损伤,主体结构未发现明显损伤. 总体上看,钢支撑- 框排架结构满足现行规范要求,抗震性能良好.
2) 采用ABAQUS建立的有限元模型与试验模型在动力特性、加速度和位移响应吻合较好,对钢支撑损伤部位和损伤程度的模拟与试验结果一致,对煤仓间沿X向布设的钢支撑进行加强后,煤仓间局部损伤情况得到缓解.
3) 试验模型第1~4层楼层加速度响应分布均匀,在第5、6层明显增大,尤其是第6层,地震动峰值加速度放大系数为3.0~4.5;钢支撑- 框排架结构X向层间位移普遍大于Y向,最大层间位移角发生在第5层;随着地震动峰值加速度的增加,钢支撑- 框排架结构扭转动力反应加大,设计时应予以注意.
4) 通过振动台试验及有限元分析结果表明,在地震作用下,采用钢支撑的电力主厂房结构破坏主要集中在结构煤仓间沿X向布置的钢支撑,这是采用钢支撑的电力主厂房结构性能的薄弱环节,建议在电力主厂房结构设计时对X向及薄弱部位钢支撑进行加强,或考虑应用防屈曲支撑,提高结构抗扭和整体耗能能力.
